2022-2023学年人教版九年级数学上册21.2.2公式法 课件(共95张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.2.2公式法 课件(共95张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 11:31:30 | ||
图片预览






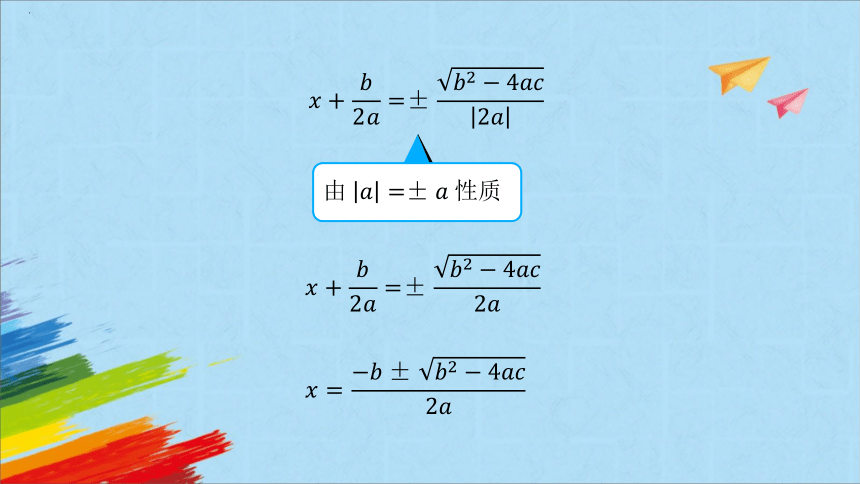
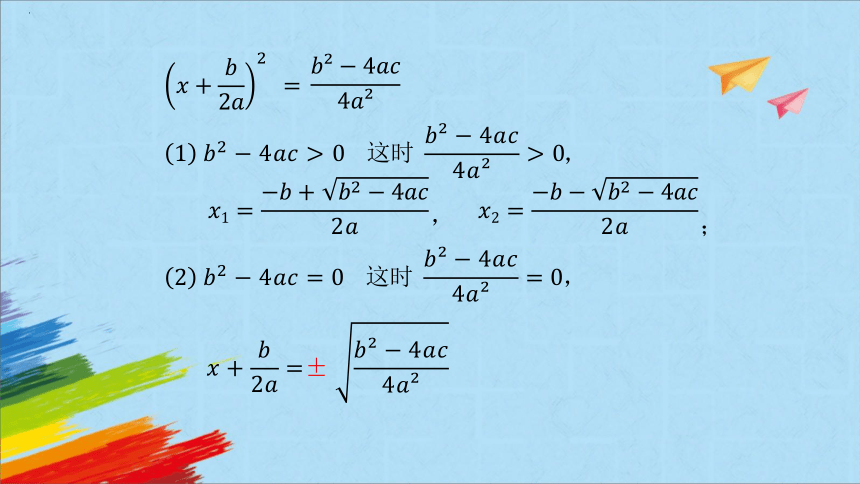
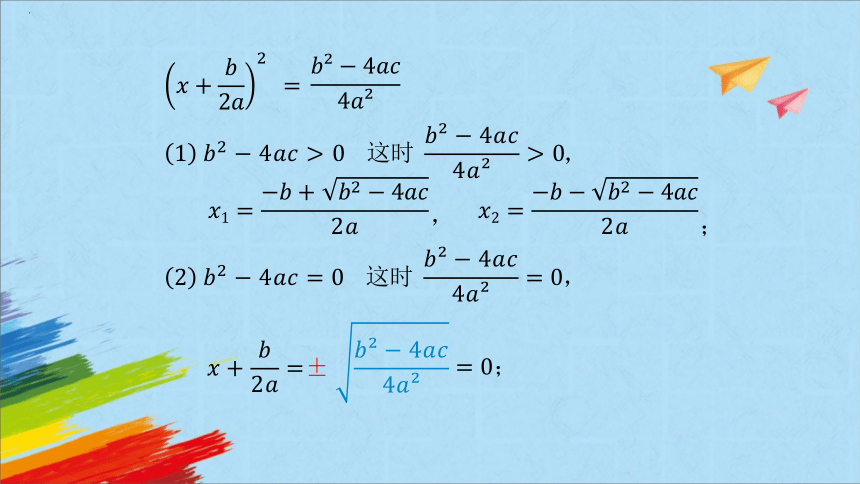
文档简介
(共95张PPT)
公式法
(第一课时)
复习回顾
问题1
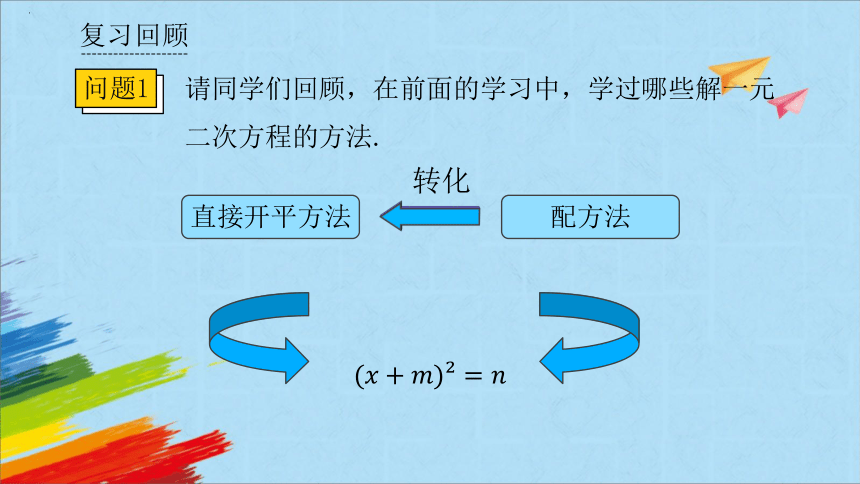
请同学们回顾,在前面的学习中,学过哪些解一元二次方程的方法.
直接开平方法
配方法
转化
复习回顾
问题2
用配方法解方程.
解:移项,得
,
.
.
配方,得
二次项系数化为,得
由此可得
,
.
.
探究新知
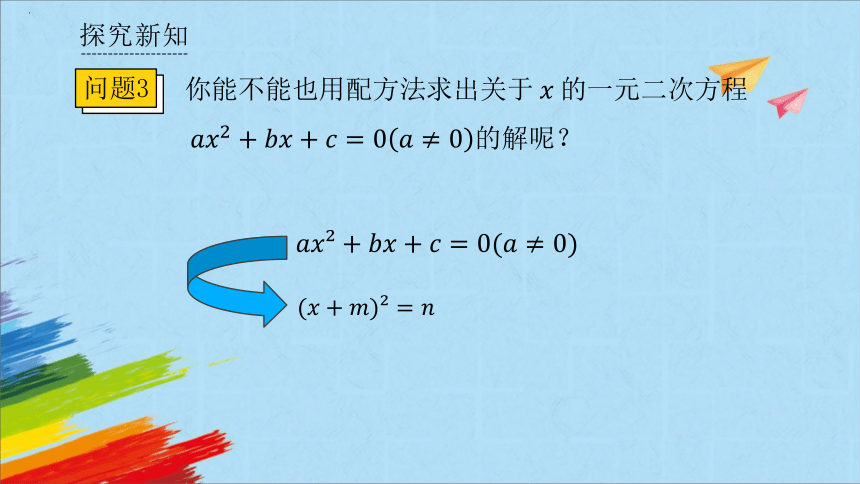
问题3
你能不能也用配方法求出关于的一元二次方程的解呢?
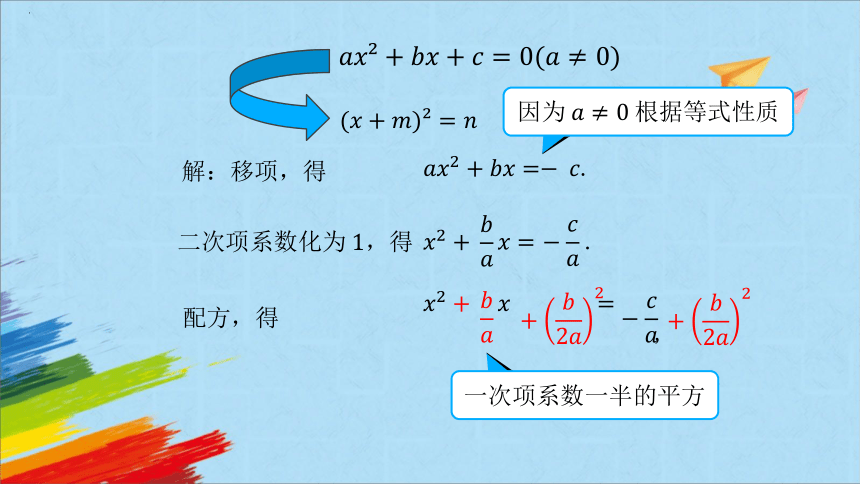
解:移项,得
.
配方,得
二次项系数化为,得
因为根据等式性质
.
一次项系数一半的平方
,
解:移项,得
.
配方,得
一次项系数一半的平方
因为根据等式性质
二次项系数化为,得
.
,
配方,得
,
,
.
配方,得
.
,有两个实数根;,方程无实根.
性质
性质
,
,
,
;
;
,
,
,
;
方程无实数根.
,
,
;
,
,
总结
关于的一元二次方程 的根的情况:
,
,
;
有两个不相等实数根;
时,
有两个相等实数根;
时,
无实数根.
;
可见,式子 决定了一元二次方程的根的情况.
可见,式子 决定了一元二次方程的根的情况. 时,一元二次方程
的实数根可写为 的形式.
当时,方程的实数根可写为 的形式,这个式子叫做一元二次方程求根公式.
解一元二次方程时,把各系数直接代入求根公式,这种
解一元二次方程的方法叫做公式法.
一元二次方程法
直接开平方法
配方法
一元二次方程法
直接开平方法
配方法
公式法
巩固落实
例
用.
解:方程
.
.
巩固落实
例
用.
解:方程
.
方程有两个不相等实数根
.
.
.
即:, .
用公式法解一元二次方程的一般步骤
1
2
化“一般形式”.
确定,,(注意符号).
用公式法解一元二次方程的一般步骤
1
2
3
化“一般形式”.
确定,,(注意符号).
计算 的值.
4
当,将,,及 代入公式 求出方程的根;
当 ,方程无实数根.
5
结果化成最简形式.
公式法
解:.
.
.
方程有两个不相等实数根
, .
.
配方法
, .
.
.
.
.
.
问题4
比较两种解法,能体会为什么学习公式法吗?
1
利用配方法可以推导出求根公式,配方是推导求根公式的中间过程.
2
公式法则省去了配方的中间过程,直接利用了配方的结果.
3
公式法的优点是操作简单,直接计算,是解一元二次方程的通法.
例3
解关于.
例3
解关于.
例3
解关于.
方法?
即:, .
例3
解关于.
解:,,.
0.
.
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
解:
0.
解方程 .
.
即: ,.
.
方程有两个不相等实数根
,得
解方程.
,.
解:移项,得
.
,
.
由此可得
,
,得
解方程.
,.
解:移项,得
.
,
.
由此可得
,
.
.
.
.
∴.
即 .
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
推导
课堂小结
发现
结论
应用
布置作业
用公式法解下列方程.
;
1
2
.
公式法
(第二课时)
复习回顾
请同学们解方程.
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程
即 , .
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程.
即 , .
小明的解法
小华的解法
配方法
.
.
.
,
, .
, ,.
.
方程
即 , .
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程.
即 , .
配方法
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程
即 , .
公式法
配方法
小明的解法
小华的解法
公式法
.
.
.
,
, .
, ,.
.
方程.
即 , .
配方法
复习回顾
关于
;
当方程的根为
当方程的根为
;
复习回顾
当方程无实数根.
关于
;
当方程的根为
当方程的根为
;
运用公式
用公式法解下列方程
;
;
.
例1
运用公式
;
例1
用公式法解下列方程
运用公式
;
例1
用公式法解下列方程
运用公式
;
例1
解:,.
.
用公式法解下列方程
运用公式
;
例1
方程有两个相等的实数根.
解:,.
.
用公式法解下列方程
运用公式
;
例1
解:,.
.
用公式法解下列方程
.
方程有两个相等的实数根.
运用公式
例1
用公式法解下列方程
运用公式
例1
用公式法解下列方程
运用公式
例1
解:化为.
.
.
用公式法解下列方程
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
,
即, .
用公式法解下列方程
解:化为.
.
运用公式
例1
解:化为.
.
.
用公式法解下列方程
.
运用公式
例1
解:化为.
.
.
方程无实数根.
用公式法解下列方程
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,将 、、及代入公式
,
方程的根.
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,方程无实数根.
,将 、、及代入公式
,
方程的根.
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,将 、、及代入公式
,
方程的根.
,方程无实数根.
5
结果化成最简形式.
关于的一元二次方程实数根的情况:
1
2
3
时,方程无实数根.
,方程有两个不等实数根;
时,方程有两个相等实数根;
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
;
运用公式
用公式法解关于的方程
例2
;
运用公式
例2
解:.
.
原方程为一元二次方程.
非负数
用公式法解关于的方程
;
运用公式
例2
解:.
.
非负数
用公式法解关于的方程
.
原方程为一元二次方程.
;
运用公式
例2
解:.
.
方程有两个实数根.
非负数
用公式法解关于的方程
.
原方程为一元二次方程.
;
运用公式
例2
即
,
.
用公式法解关于的方程
.
.
运用公式
例2
用公式法解关于的方程
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
解:
.
.
原方程为一元二次方程.
.
用公式法解关于的方程
.
运用公式
例2
解:.
.
.
原方程为一元二次方程.
方程有两个实数根.
用公式法解关于的方程
.
.
运用公式
例2
,
用公式法解关于的方程
.
运用公式
例2
,
分式化简
,
.
.
用公式法解关于的方程
.
即
运用公式
用公式法解下列方程
; ;
.
例1
;
用公式法解关于 的方程
例2
.
运用公式
都是一元二次方程;
用公式法都可以求出这些方程的根.
相同点
不同点
例是数字系数,例是字母系数;
例是数的运算,例是式的运算比较多;
例判别式 的结果是一个数,
例判别式的结果是一个式子.
课堂小结
本节课,主要练习了用公式法解一元二次方程;
1
一元二次方程根的情况与判别式 的符号的关系;
2
要熟记求根公式.
3
课堂小结
关于的一元二次方程
时,方程的根为
时,
无实数根.
;
时,方程的根为
一元二次方程法
直接开平方法
配方法
公式法
课堂小结
布置作业
用的方程
;
;
.
布置作业
用的方程;
解:.
布置作业
解:.
方程有两个不等实数根.
.
, .
用的方程;
布置作业
用的方程.
解:.
方程有两个实数根.
.
.
, .
公式法
(第一课时)
复习回顾
问题1
请同学们回顾,在前面的学习中,学过哪些解一元二次方程的方法.
直接开平方法
配方法
转化
复习回顾
问题2
用配方法解方程.
解:移项,得
,
.
.
配方,得
二次项系数化为,得
由此可得
,
.
.
探究新知
问题3
你能不能也用配方法求出关于的一元二次方程的解呢?
解:移项,得
.
配方,得
二次项系数化为,得
因为根据等式性质
.
一次项系数一半的平方
,
解:移项,得
.
配方,得
一次项系数一半的平方
因为根据等式性质
二次项系数化为,得
.
,
配方,得
,
,
.
配方,得
.
,有两个实数根;,方程无实根.
性质
性质
,
,
,
;
;
,
,
,
;
方程无实数根.
,
,
;
,
,
总结
关于的一元二次方程 的根的情况:
,
,
;
有两个不相等实数根;
时,
有两个相等实数根;
时,
无实数根.
;
可见,式子 决定了一元二次方程的根的情况.
可见,式子 决定了一元二次方程的根的情况. 时,一元二次方程
的实数根可写为 的形式.
当时,方程的实数根可写为 的形式,这个式子叫做一元二次方程求根公式.
解一元二次方程时,把各系数直接代入求根公式,这种
解一元二次方程的方法叫做公式法.
一元二次方程法
直接开平方法
配方法
一元二次方程法
直接开平方法
配方法
公式法
巩固落实
例
用.
解:方程
.
.
巩固落实
例
用.
解:方程
.
方程有两个不相等实数根
.
.
.
即:, .
用公式法解一元二次方程的一般步骤
1
2
化“一般形式”.
确定,,(注意符号).
用公式法解一元二次方程的一般步骤
1
2
3
化“一般形式”.
确定,,(注意符号).
计算 的值.
4
当,将,,及 代入公式 求出方程的根;
当 ,方程无实数根.
5
结果化成最简形式.
公式法
解:.
.
.
方程有两个不相等实数根
, .
.
配方法
, .
.
.
.
.
.
问题4
比较两种解法,能体会为什么学习公式法吗?
1
利用配方法可以推导出求根公式,配方是推导求根公式的中间过程.
2
公式法则省去了配方的中间过程,直接利用了配方的结果.
3
公式法的优点是操作简单,直接计算,是解一元二次方程的通法.
例3
解关于.
例3
解关于.
例3
解关于.
方法?
即:, .
例3
解关于.
解:,,.
0.
.
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
解:
0.
解方程 .
.
即: ,.
.
方程有两个不相等实数根
,得
解方程.
,.
解:移项,得
.
,
.
由此可得
,
,得
解方程.
,.
解:移项,得
.
,
.
由此可得
,
.
.
.
.
∴.
即 .
课堂练习
已知一元二次方程的较小的根为 ,下面对 的估计正确的是( ).
推导
课堂小结
发现
结论
应用
布置作业
用公式法解下列方程.
;
1
2
.
公式法
(第二课时)
复习回顾
请同学们解方程.
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程
即 , .
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程.
即 , .
小明的解法
小华的解法
配方法
.
.
.
,
, .
, ,.
.
方程
即 , .
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程.
即 , .
配方法
小明的解法
小华的解法
.
.
.
,
, .
, ,.
.
方程
即 , .
公式法
配方法
小明的解法
小华的解法
公式法
.
.
.
,
, .
, ,.
.
方程.
即 , .
配方法
复习回顾
关于
;
当方程的根为
当方程的根为
;
复习回顾
当方程无实数根.
关于
;
当方程的根为
当方程的根为
;
运用公式
用公式法解下列方程
;
;
.
例1
运用公式
;
例1
用公式法解下列方程
运用公式
;
例1
用公式法解下列方程
运用公式
;
例1
解:,.
.
用公式法解下列方程
运用公式
;
例1
方程有两个相等的实数根.
解:,.
.
用公式法解下列方程
运用公式
;
例1
解:,.
.
用公式法解下列方程
.
方程有两个相等的实数根.
运用公式
例1
用公式法解下列方程
运用公式
例1
用公式法解下列方程
运用公式
例1
解:化为.
.
.
用公式法解下列方程
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
用公式法解下列方程
解:化为.
运用公式
例1
.
.
方程有两个不等的实数根.
,
即, .
用公式法解下列方程
解:化为.
.
运用公式
例1
解:化为.
.
.
用公式法解下列方程
.
运用公式
例1
解:化为.
.
.
方程无实数根.
用公式法解下列方程
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,将 、、及代入公式
,
方程的根.
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,方程无实数根.
,将 、、及代入公式
,
方程的根.
用公式法解一元二次方程的一般步骤:
化为“一般形式”.
1
2
确定 、、(注意符号).
3
计算值.
4
,将 、、及代入公式
,
方程的根.
,方程无实数根.
5
结果化成最简形式.
关于的一元二次方程实数根的情况:
1
2
3
时,方程无实数根.
,方程有两个不等实数根;
时,方程有两个相等实数根;
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
一般的,式子叫做一元二次方程根的判别式,通常用希腊字母“”表示它,即 .
;
运用公式
用公式法解关于的方程
例2
;
运用公式
例2
解:.
.
原方程为一元二次方程.
非负数
用公式法解关于的方程
;
运用公式
例2
解:.
.
非负数
用公式法解关于的方程
.
原方程为一元二次方程.
;
运用公式
例2
解:.
.
方程有两个实数根.
非负数
用公式法解关于的方程
.
原方程为一元二次方程.
;
运用公式
例2
即
,
.
用公式法解关于的方程
.
.
运用公式
例2
用公式法解关于的方程
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
用公式法解关于的方程
.
运用公式
例2
解:
.
.
原方程为一元二次方程.
.
用公式法解关于的方程
.
运用公式
例2
解:.
.
.
原方程为一元二次方程.
方程有两个实数根.
用公式法解关于的方程
.
.
运用公式
例2
,
用公式法解关于的方程
.
运用公式
例2
,
分式化简
,
.
.
用公式法解关于的方程
.
即
运用公式
用公式法解下列方程
; ;
.
例1
;
用公式法解关于 的方程
例2
.
运用公式
都是一元二次方程;
用公式法都可以求出这些方程的根.
相同点
不同点
例是数字系数,例是字母系数;
例是数的运算,例是式的运算比较多;
例判别式 的结果是一个数,
例判别式的结果是一个式子.
课堂小结
本节课,主要练习了用公式法解一元二次方程;
1
一元二次方程根的情况与判别式 的符号的关系;
2
要熟记求根公式.
3
课堂小结
关于的一元二次方程
时,方程的根为
时,
无实数根.
;
时,方程的根为
一元二次方程法
直接开平方法
配方法
公式法
课堂小结
布置作业
用的方程
;
;
.
布置作业
用的方程;
解:.
布置作业
解:.
方程有两个不等实数根.
.
, .
用的方程;
布置作业
用的方程.
解:.
方程有两个实数根.
.
.
, .
同课章节目录
