人教版九年级下册 26.1.2反比例函数的图象和性质 课件(共33张PPT)
文档属性
| 名称 | 人教版九年级下册 26.1.2反比例函数的图象和性质 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 15:24:04 | ||
图片预览






文档简介
(共33张PPT)
26.1 反比例函数
第26章 反比例函数
26.1.2 反比例函数的图象和性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
反比例函数的图象
反比例函数的性质
反比例函数 (k ≠ 0)中k 的几何性质
知识点
反比例函数的图象
知1-讲
感悟新知
1
1. 图象的画法(描点法):
(1)列表:先取一些自变量的值,在原点的两边取三对或三对以上互为相反数的值.
(2)描点:根据表中提供的数据,即点的坐标,在平面直角坐标系中描出对应的点.
(3)连线:用平滑的曲线顺次把这些点连接起来并延伸.
知1-讲
感悟新知
2. 图象的特点:
(1)反比例函数 (k 为常数,k ≠ 0)的图象是双曲线.
(2)反比例函数图象的两支分别位于第一、第三象限或第二、第四象限.
(3)双曲线的两支都无限接近坐标轴,但永远不与坐标轴相交.
知1-讲
感悟新知
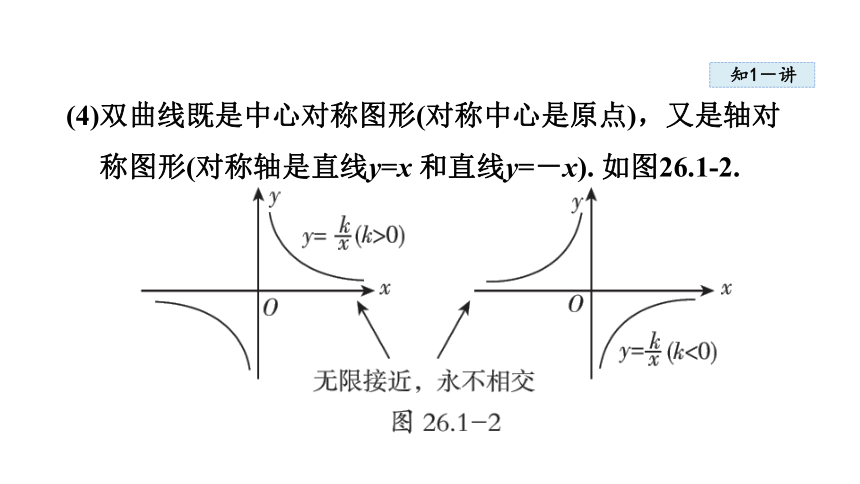
(4)双曲线既是中心对称图形(对称中心是原点),又是轴对称图形(对称轴是直线y=x 和直线y=-x). 如图26.1-2.
知1-讲
感悟新知
特别提醒
●由于反比例函数图象的两个分支关于原点对称,所以只要画出它在一个象限内的分支,就可以对称地画出另一个分支.
●画实际问题中的反比例函数的图象时,要考虑自变量取值范围的限制,一般地,实际问题的图象是反比例函数图象在第一象限内的一支或其中一部分.
感悟新知
知1-练
在同一平面直角坐标系中画出反比例函数y= 和y=- 的图象.
例 1
解题秘方:紧扣画图象的步骤“一列、二描、三连”作图.
感悟新知
知1-练
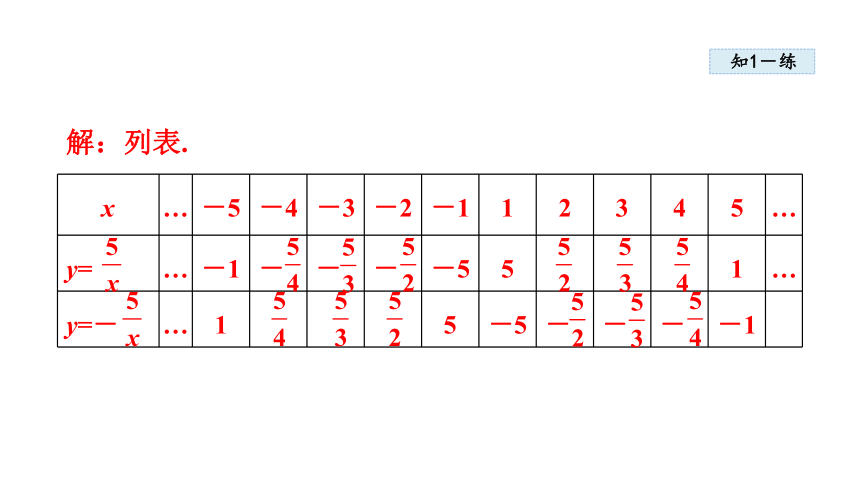
解:列表.
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y= … -1 - - - -5 5 1 …
y=- … 1 5 -5 - - - -1
感悟新知
知1-练
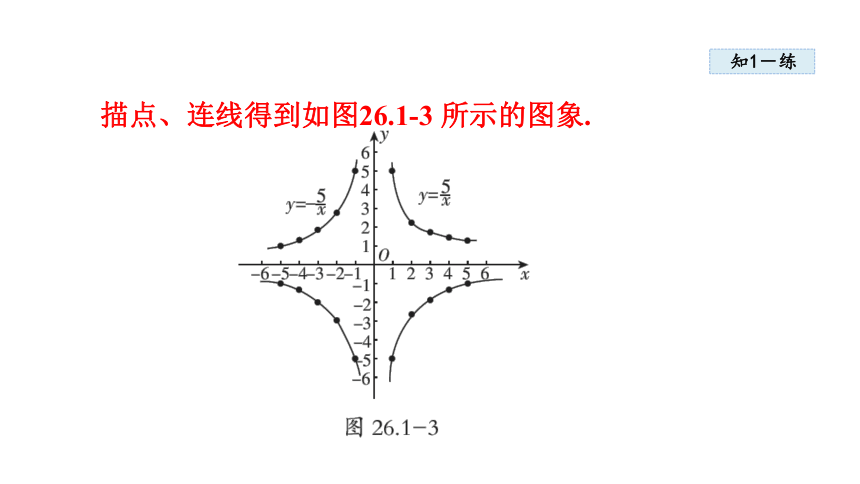
描点、连线得到如图26.1-3 所示的图象.
感悟新知
知1-练
1-1. 已知函数y=(m-2)·xm2-5 是反比例函数.
(1)求m 的值.
感悟新知
知1-练
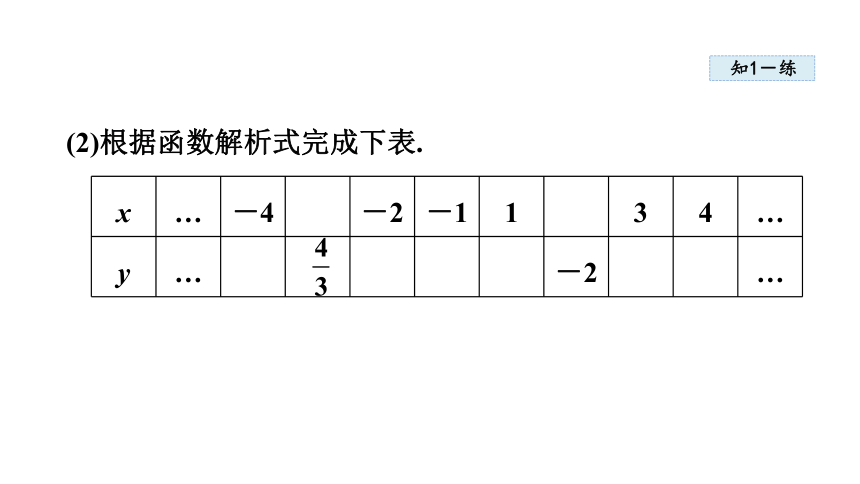
(2)根据函数解析式完成下表.
x … -4 -2 -1 1 3 4 …
y … -2 …
感悟新知
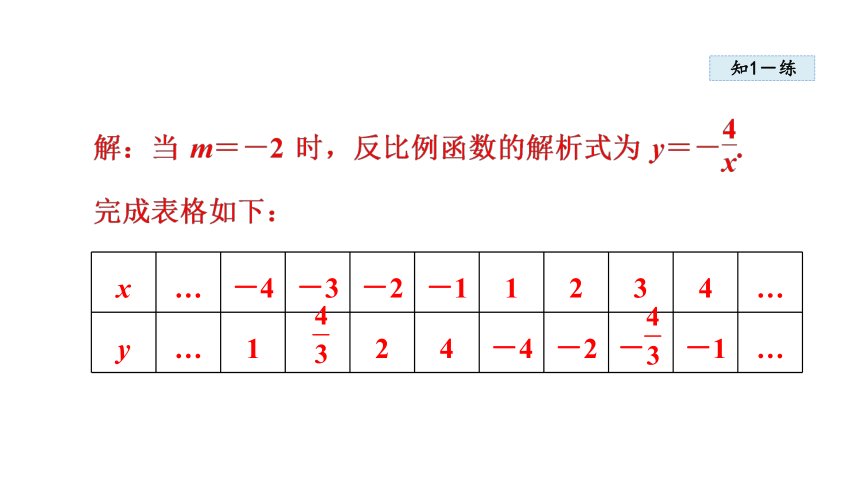
知1-练
x … -4 -3 -2 -1 1 2 3 4 …
y … 1 2 4 -4 -2 - -1 …
感悟新知
知1-练
(3)以表中各组对应值为点的坐标,在如图所示的平面直角坐标系中描点并画出函数图象.
感悟新知
知1-练
解:函数图象如图所示.
知识点
反比例函数的性质
知2-讲
感悟新知
2
反比例函数的性质主要研究它的图象的位置和函数值的增减情况,如下表所示.
特别提醒
在描述反比例函数的增减性时,必须指明“在每一个象限内”.因为当k > 0(k < 0) 时,整个函数不是y随x的增大而减小( 增大),而是函数在每一个象限内,y随x的增大而减小(增大),所以笼统地说“对于函数y= ,y 随x的增大而减小”是错误的.
知2-讲
感悟新知
反比例函数 (k ≠ 0) k的符号 k > 0 k < 0
图象
图象位置 第一、第三象限 第二、第四象限
增减性 在每一个象限内,y 随x的增大而减小 在每一个象限内,y 随x的增大而增大
感悟新知
知2-练
已知反比例函数y= (m≠0)的图象过点(-3,-12),
且反比例函数y= 的图象位于第二、第四象限.
(1)求m 的值;
(2)对于y= ,当x ﹥ 2 时,求y 的取值范围.
例2
解题秘方:紧扣“k 的符号、双曲线的位置、函数的增减性三者相互依存,知一推二”这一规律解题.
知2-讲
感悟新知
解:(1)把点(-3,-12)的坐标代入y= 中,
得-12= ,∴ m2=36,∴ m=±6.
∵反比例函数y= 的图象位于第二、第四象限,
∴ m<0. ∴ m=-6.
感悟新知
知2-练
(2)由m=-6 知反比例函数y= 的表达式为y=- .
∵ x>2,∴此部分图象在第四象限.
当x=2 时,y=- =-3. ∵在第四象限内,y 随x 的增大而增大,∴当x>2 时,-3感悟新知
知2-练
2-1.[中考· 成都] 在平面直角坐标系xOy 中,若反比例函数y= 的图象位于第二、四象限, 则k 的取值范围是________.
k<2
感悟新知
知2-练
2-2.[中考· 武汉]若点A(a-1,y1),B(a+1,y2)在反比例函数y= (k < 0)的图象上,且y1 > y2,则a的取值范围是( )
A.a < -1
B. -1 < a < 1
C.a > 1
D.a < -1 或a > 1
B
知识点
反比例函数y= (k≠0)中k的几何性质
知3-讲
感悟新知
3
1. 矩形的面积: 如图26.1-4, 过双曲线y= 上任意一点P(x,y)分别作x 轴、y 轴的垂线PM,PN,所得的矩形PMON的面积S=PM·PN=|y|·|x|=|xy|. 因为y= ,
所以xy=k, 所以S=|k|,即过双曲线上任意
一点作x 轴、y 轴的垂线,所得矩形的面积
为| k |.
知3-讲
感悟新知
2. 三角形的面积: 如图26.1-4, 过双曲线y= 上任意一点E 作EF 垂直于y 轴, 垂足为F, 连接EO, 则S △ EOF= , 即过双曲线上任意一点作一坐标轴的垂线,连接该点与原点,所得三角形的面积为 .
知3-讲
感悟新知
特别提醒
●在利用反比例函数y= (k ≠ 0) 中k的几何性质确定k的值时,不仅要注意矩形面积的大小,还要注意函数图象的位置.
●因为y= (k≠0)中k有正、负之分,所以在利用k求矩形或三角形面积时,都要加上绝对值符号.
感悟新知
知3-练
[中考· 齐齐哈尔] 如图26.1-5 所示,点A 是反比例函数图象上一点,过点A作AB ⊥ y 轴于点B,点C,D 在x 轴上,且BC ∥ AD,四边形
ABCD 的面积为3,则这个反比例
函数的解析式为__________.
例 3
感悟新知
知3-练
解题秘方:紧扣“k 的几何性质”,用“等面积法”将四边形的面积转化为符合k 的几何性质的矩形面积来求解.
感悟新知
知3-练
解:设这个反比例函数的解析式为y= (k ≠ 0),过
点A 向x 轴作垂线,垂足为E,如图26.1-5 所示. 易知四边形ABCD 为平行四边形,根据反比例函数中k 的几何性质,可得|k|=S四边形AEOB=S四边形ABCD=3.
∵函数图象有一支在第二象限,
∴ k=-3,即函数的解析式为y=- .
感悟新知
知3-练
3-1. [中考 锦州]如图, 在矩形OABC中,A(1,0),C(0,2), 双曲线y= (0A
感悟新知
知3-练
[中考·永州] 如图26.1-6,两个反比例函数y= 和y= 在第一象限内的图象分别是C1 和C2,设点P 在C1 上,PA ⊥ x 轴于点A,交C2 于点B,
则△ POB 的面积为________.
例4
1
感悟新知
知3-练
解题秘方:紧扣“k 的几何性质”,用“作差法”将阴影部分的面积转化为符合k 的几何性质的三角形面积的差来求解.
感悟新知
知3-练
解:根据反比例函数中比例系数k 的几何性质,
可得SRt △ POA= ×4=2,SRt △ BOA= ×2=1.
所以S△ POB=SRt △ POA-SRt △ BOA=2-1=1.
感悟新知
知3-练
4-1. 如图, 点A 是反比例函数y= (x >0)的图象上的一点,过点A 作AC ⊥ y 轴,垂足为点C,AC 交反比例函数y= 的图象于点B,点P 是x 轴上的动点,则△ PAB 的面积为( )
A.2 B.4
C.6 D.8
A
课堂小结
反比例函数的图象和性质
反比例函数的图象和性质
正负性决定图象的位置
两个变量的变化规律
绝对值决定几何图形的面积
26.1 反比例函数
第26章 反比例函数
26.1.2 反比例函数的图象和性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
反比例函数的图象
反比例函数的性质
反比例函数 (k ≠ 0)中k 的几何性质
知识点
反比例函数的图象
知1-讲
感悟新知
1
1. 图象的画法(描点法):
(1)列表:先取一些自变量的值,在原点的两边取三对或三对以上互为相反数的值.
(2)描点:根据表中提供的数据,即点的坐标,在平面直角坐标系中描出对应的点.
(3)连线:用平滑的曲线顺次把这些点连接起来并延伸.
知1-讲
感悟新知
2. 图象的特点:
(1)反比例函数 (k 为常数,k ≠ 0)的图象是双曲线.
(2)反比例函数图象的两支分别位于第一、第三象限或第二、第四象限.
(3)双曲线的两支都无限接近坐标轴,但永远不与坐标轴相交.
知1-讲
感悟新知
(4)双曲线既是中心对称图形(对称中心是原点),又是轴对称图形(对称轴是直线y=x 和直线y=-x). 如图26.1-2.
知1-讲
感悟新知
特别提醒
●由于反比例函数图象的两个分支关于原点对称,所以只要画出它在一个象限内的分支,就可以对称地画出另一个分支.
●画实际问题中的反比例函数的图象时,要考虑自变量取值范围的限制,一般地,实际问题的图象是反比例函数图象在第一象限内的一支或其中一部分.
感悟新知
知1-练
在同一平面直角坐标系中画出反比例函数y= 和y=- 的图象.
例 1
解题秘方:紧扣画图象的步骤“一列、二描、三连”作图.
感悟新知
知1-练
解:列表.
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y= … -1 - - - -5 5 1 …
y=- … 1 5 -5 - - - -1
感悟新知
知1-练
描点、连线得到如图26.1-3 所示的图象.
感悟新知
知1-练
1-1. 已知函数y=(m-2)·xm2-5 是反比例函数.
(1)求m 的值.
感悟新知
知1-练
(2)根据函数解析式完成下表.
x … -4 -2 -1 1 3 4 …
y … -2 …
感悟新知
知1-练
x … -4 -3 -2 -1 1 2 3 4 …
y … 1 2 4 -4 -2 - -1 …
感悟新知
知1-练
(3)以表中各组对应值为点的坐标,在如图所示的平面直角坐标系中描点并画出函数图象.
感悟新知
知1-练
解:函数图象如图所示.
知识点
反比例函数的性质
知2-讲
感悟新知
2
反比例函数的性质主要研究它的图象的位置和函数值的增减情况,如下表所示.
特别提醒
在描述反比例函数的增减性时,必须指明“在每一个象限内”.因为当k > 0(k < 0) 时,整个函数不是y随x的增大而减小( 增大),而是函数在每一个象限内,y随x的增大而减小(增大),所以笼统地说“对于函数y= ,y 随x的增大而减小”是错误的.
知2-讲
感悟新知
反比例函数 (k ≠ 0) k的符号 k > 0 k < 0
图象
图象位置 第一、第三象限 第二、第四象限
增减性 在每一个象限内,y 随x的增大而减小 在每一个象限内,y 随x的增大而增大
感悟新知
知2-练
已知反比例函数y= (m≠0)的图象过点(-3,-12),
且反比例函数y= 的图象位于第二、第四象限.
(1)求m 的值;
(2)对于y= ,当x ﹥ 2 时,求y 的取值范围.
例2
解题秘方:紧扣“k 的符号、双曲线的位置、函数的增减性三者相互依存,知一推二”这一规律解题.
知2-讲
感悟新知
解:(1)把点(-3,-12)的坐标代入y= 中,
得-12= ,∴ m2=36,∴ m=±6.
∵反比例函数y= 的图象位于第二、第四象限,
∴ m<0. ∴ m=-6.
感悟新知
知2-练
(2)由m=-6 知反比例函数y= 的表达式为y=- .
∵ x>2,∴此部分图象在第四象限.
当x=2 时,y=- =-3. ∵在第四象限内,y 随x 的增大而增大,∴当x>2 时,-3
知2-练
2-1.[中考· 成都] 在平面直角坐标系xOy 中,若反比例函数y= 的图象位于第二、四象限, 则k 的取值范围是________.
k<2
感悟新知
知2-练
2-2.[中考· 武汉]若点A(a-1,y1),B(a+1,y2)在反比例函数y= (k < 0)的图象上,且y1 > y2,则a的取值范围是( )
A.a < -1
B. -1 < a < 1
C.a > 1
D.a < -1 或a > 1
B
知识点
反比例函数y= (k≠0)中k的几何性质
知3-讲
感悟新知
3
1. 矩形的面积: 如图26.1-4, 过双曲线y= 上任意一点P(x,y)分别作x 轴、y 轴的垂线PM,PN,所得的矩形PMON的面积S=PM·PN=|y|·|x|=|xy|. 因为y= ,
所以xy=k, 所以S=|k|,即过双曲线上任意
一点作x 轴、y 轴的垂线,所得矩形的面积
为| k |.
知3-讲
感悟新知
2. 三角形的面积: 如图26.1-4, 过双曲线y= 上任意一点E 作EF 垂直于y 轴, 垂足为F, 连接EO, 则S △ EOF= , 即过双曲线上任意一点作一坐标轴的垂线,连接该点与原点,所得三角形的面积为 .
知3-讲
感悟新知
特别提醒
●在利用反比例函数y= (k ≠ 0) 中k的几何性质确定k的值时,不仅要注意矩形面积的大小,还要注意函数图象的位置.
●因为y= (k≠0)中k有正、负之分,所以在利用k求矩形或三角形面积时,都要加上绝对值符号.
感悟新知
知3-练
[中考· 齐齐哈尔] 如图26.1-5 所示,点A 是反比例函数图象上一点,过点A作AB ⊥ y 轴于点B,点C,D 在x 轴上,且BC ∥ AD,四边形
ABCD 的面积为3,则这个反比例
函数的解析式为__________.
例 3
感悟新知
知3-练
解题秘方:紧扣“k 的几何性质”,用“等面积法”将四边形的面积转化为符合k 的几何性质的矩形面积来求解.
感悟新知
知3-练
解:设这个反比例函数的解析式为y= (k ≠ 0),过
点A 向x 轴作垂线,垂足为E,如图26.1-5 所示. 易知四边形ABCD 为平行四边形,根据反比例函数中k 的几何性质,可得|k|=S四边形AEOB=S四边形ABCD=3.
∵函数图象有一支在第二象限,
∴ k=-3,即函数的解析式为y=- .
感悟新知
知3-练
3-1. [中考 锦州]如图, 在矩形OABC中,A(1,0),C(0,2), 双曲线y= (0
感悟新知
知3-练
[中考·永州] 如图26.1-6,两个反比例函数y= 和y= 在第一象限内的图象分别是C1 和C2,设点P 在C1 上,PA ⊥ x 轴于点A,交C2 于点B,
则△ POB 的面积为________.
例4
1
感悟新知
知3-练
解题秘方:紧扣“k 的几何性质”,用“作差法”将阴影部分的面积转化为符合k 的几何性质的三角形面积的差来求解.
感悟新知
知3-练
解:根据反比例函数中比例系数k 的几何性质,
可得SRt △ POA= ×4=2,SRt △ BOA= ×2=1.
所以S△ POB=SRt △ POA-SRt △ BOA=2-1=1.
感悟新知
知3-练
4-1. 如图, 点A 是反比例函数y= (x >0)的图象上的一点,过点A 作AC ⊥ y 轴,垂足为点C,AC 交反比例函数y= 的图象于点B,点P 是x 轴上的动点,则△ PAB 的面积为( )
A.2 B.4
C.6 D.8
A
课堂小结
反比例函数的图象和性质
反比例函数的图象和性质
正负性决定图象的位置
两个变量的变化规律
绝对值决定几何图形的面积
