人教版九年级下册27.2.2相似三角形的性质 课件(共18张PPT)
文档属性
| 名称 | 人教版九年级下册27.2.2相似三角形的性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 949.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 11:30:24 | ||
图片预览





文档简介
(共18张PPT)
27.2 相似三角形
第27章 相似
27.2.2 相似三角形的性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
相似三角形对应线段的比
相似三角形面积的比
知识点
相似三角形对应线段的比
知1-讲
感悟新知
1
1. 定理:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
即:相似三角形对应线段的比等于相似比.
深度理解
对应高、对应中线与对应角平分线分别是指相似三角形对应边上的高、中线与对应内角的平分线.
知1-讲
感悟新知
特别提醒:(1)注意“对应”二字,应用时要找准对应线段;(2)相似比是有顺序的,不能颠倒相似三角形中元素的顺序.
2. 相似三角形周长的比:相似三角形周长的比等于它们的相似比.
感悟新知
知1-练
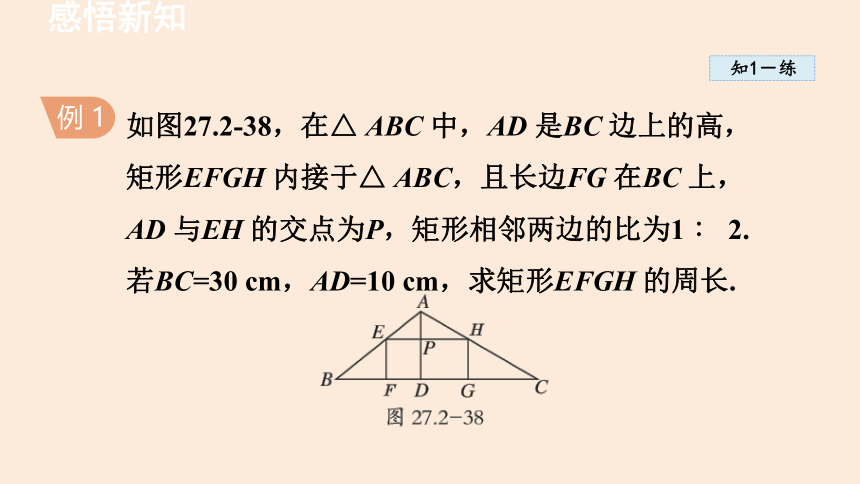
如图27.2-38,在△ ABC 中,AD 是BC 边上的高,矩形EFGH 内接于△ ABC,且长边FG 在BC 上,AD 与EH 的交点为P,矩形相邻两边的比为1 ∶ 2. 若BC=30 cm,AD=10 cm,求矩形EFGH 的周长.
例 1
感悟新知
知1-练
解题秘方:利用相似三角形对应高的比等于相似比求解.
感悟新知
知1-练
解:设HG=x cm,则EH=2x cm.
易得AP ⊥ EH,PD=HG.
∵ AD=10 cm,∴ AP=(10-x)cm.
∵四边形EFGH 为矩形,
∴ EH ∥ BC. ∴△ AEH ∽△ ABC.
∴
解得x=6. ∴ HG=6 cm,EH=12 cm.
∴矩形EFGH 的周长为(12+6)×2=36 (cm).
感悟新知
知1-练
1-1. 如图, △ ABC ∽△ A ′B ′C ′,AD,BE分别是△ ABC 的高和中线,A′D′,B′E′分别是△ A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,则B′E′的长为( )
D
感悟新知
知1-练
如果两个相似三角形的相似比是3 ∶ 2,它们的周长差为8,那么较大的三角形的周长为________.
例2
解题秘方:利用相似三角形对应高的比等于相似比求解.
24
也可设较小的三角形的周长为
2x,较大的三角形的周长为3x.
∴ 3x-2x=8,∴ x=8,
∴较大的三角形的周长为3x=24.
感悟新知
知1-练
解:设较大的三角形的周长为x,则较小的三角形的周长为x-8.
∵这两个相似三角形的相似比为3 ∶ 2,
∴这两个三角形的周长比为3 ∶ 2,
∴ ,解得x=24.
感悟新知
知1-练
2-1. 已知两个相似三角形的对应边之比为1 ∶ 3,则它们的周长比为( )
A.1 ∶ 9 B.9 ∶ 1
C.1 ∶ 6 D.1 ∶ 3
D
感悟新知
知1-练
2-2. 若△ABC∽△A′B′C′,且 ,△ ABC的周长为15 cm, 则△A′B′C′的周长为( )
A. 18 cm B. 20 cm
C. cm D. cm
B
知识点
相似三角形面积的比
知2-讲
感悟新知
2
1. 相似三角形面积的比:相似三角形面积的比等于相似比的平方.若△ ABC ∽△ A′B′C′,且它们的相似比为k,则
2. 相似多边形面积的比:相似多边形面积的比等于相似比的平方.
知2-讲
感悟新知
特别提醒
面积的比是相似比的平方,不要与对应线段的比、周长的比等于相似比混淆.
感悟新知
知2-练
如图27.2-39,△ ABC ∽△ A′B′C′,BC=6,B′C′=4,
AD ⊥ BC 于点D,AD=4,求△ A′B′C′的面积.
解题秘方:利用相似三角形面积的比等于相似比的平方求解.
例 3
知2-讲
感悟新知
解:S△ ABC= BC·AD= ×6×4=12.
∵△ ABC ∽△ A′B′C′,∴
即
∴ 即△ A′B′C′的面积为 .
不要误认为相似三角形面积
的比等于相似比.
感悟新知
知2-练
3-1. [中考· 遂宁]如图,在△ ABC 中, 点D,E 分别是AB,AC 的中点,若△ ADE 的面积是3 cm2,则四边形BDEC的面积为( )
A.12 cm2 B.9 cm2
C.6 cm2 D.3 cm2
B
课堂小结
相似三角形的性质
相似比
面积
对应线段
周长
相似三角形的性质
27.2 相似三角形
第27章 相似
27.2.2 相似三角形的性质
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
相似三角形对应线段的比
相似三角形面积的比
知识点
相似三角形对应线段的比
知1-讲
感悟新知
1
1. 定理:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
即:相似三角形对应线段的比等于相似比.
深度理解
对应高、对应中线与对应角平分线分别是指相似三角形对应边上的高、中线与对应内角的平分线.
知1-讲
感悟新知
特别提醒:(1)注意“对应”二字,应用时要找准对应线段;(2)相似比是有顺序的,不能颠倒相似三角形中元素的顺序.
2. 相似三角形周长的比:相似三角形周长的比等于它们的相似比.
感悟新知
知1-练
如图27.2-38,在△ ABC 中,AD 是BC 边上的高,矩形EFGH 内接于△ ABC,且长边FG 在BC 上,AD 与EH 的交点为P,矩形相邻两边的比为1 ∶ 2. 若BC=30 cm,AD=10 cm,求矩形EFGH 的周长.
例 1
感悟新知
知1-练
解题秘方:利用相似三角形对应高的比等于相似比求解.
感悟新知
知1-练
解:设HG=x cm,则EH=2x cm.
易得AP ⊥ EH,PD=HG.
∵ AD=10 cm,∴ AP=(10-x)cm.
∵四边形EFGH 为矩形,
∴ EH ∥ BC. ∴△ AEH ∽△ ABC.
∴
解得x=6. ∴ HG=6 cm,EH=12 cm.
∴矩形EFGH 的周长为(12+6)×2=36 (cm).
感悟新知
知1-练
1-1. 如图, △ ABC ∽△ A ′B ′C ′,AD,BE分别是△ ABC 的高和中线,A′D′,B′E′分别是△ A′B′C′的高和中线,且AD=4,A′D′=3,BE=6,则B′E′的长为( )
D
感悟新知
知1-练
如果两个相似三角形的相似比是3 ∶ 2,它们的周长差为8,那么较大的三角形的周长为________.
例2
解题秘方:利用相似三角形对应高的比等于相似比求解.
24
也可设较小的三角形的周长为
2x,较大的三角形的周长为3x.
∴ 3x-2x=8,∴ x=8,
∴较大的三角形的周长为3x=24.
感悟新知
知1-练
解:设较大的三角形的周长为x,则较小的三角形的周长为x-8.
∵这两个相似三角形的相似比为3 ∶ 2,
∴这两个三角形的周长比为3 ∶ 2,
∴ ,解得x=24.
感悟新知
知1-练
2-1. 已知两个相似三角形的对应边之比为1 ∶ 3,则它们的周长比为( )
A.1 ∶ 9 B.9 ∶ 1
C.1 ∶ 6 D.1 ∶ 3
D
感悟新知
知1-练
2-2. 若△ABC∽△A′B′C′,且 ,△ ABC的周长为15 cm, 则△A′B′C′的周长为( )
A. 18 cm B. 20 cm
C. cm D. cm
B
知识点
相似三角形面积的比
知2-讲
感悟新知
2
1. 相似三角形面积的比:相似三角形面积的比等于相似比的平方.若△ ABC ∽△ A′B′C′,且它们的相似比为k,则
2. 相似多边形面积的比:相似多边形面积的比等于相似比的平方.
知2-讲
感悟新知
特别提醒
面积的比是相似比的平方,不要与对应线段的比、周长的比等于相似比混淆.
感悟新知
知2-练
如图27.2-39,△ ABC ∽△ A′B′C′,BC=6,B′C′=4,
AD ⊥ BC 于点D,AD=4,求△ A′B′C′的面积.
解题秘方:利用相似三角形面积的比等于相似比的平方求解.
例 3
知2-讲
感悟新知
解:S△ ABC= BC·AD= ×6×4=12.
∵△ ABC ∽△ A′B′C′,∴
即
∴ 即△ A′B′C′的面积为 .
不要误认为相似三角形面积
的比等于相似比.
感悟新知
知2-练
3-1. [中考· 遂宁]如图,在△ ABC 中, 点D,E 分别是AB,AC 的中点,若△ ADE 的面积是3 cm2,则四边形BDEC的面积为( )
A.12 cm2 B.9 cm2
C.6 cm2 D.3 cm2
B
课堂小结
相似三角形的性质
相似比
面积
对应线段
周长
相似三角形的性质
