人教版数学 九年级下册27.3位似 课件(共39张PPT)
文档属性
| 名称 | 人教版数学 九年级下册27.3位似 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 11:30:01 | ||
图片预览









文档简介
(共39张PPT)
27.3 位似
第27章 相似
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
位似图形的定义
位似图形的性质
位似图形的画法
平面直角坐标系中的位似
知识点
位似图形的定义
知1-讲
感悟新知
1
1. 定义:如果一个图形上的点A,B,…,P,…和另一个图形上的点A′,B′,…,P′,…分别对应,并且它们的连线AA′,BB′,…,PP′,…都经过同一点O,
…,那么这两个图形叫做位似图形,点O 是位似中心.
知1-讲
感悟新知
2. 位似与相似的关系:
(1)相似仅要求两个图形形状完全相同,而位似是在相似的基础上要求对应顶点的连线相交于一点.
(2)如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,因此, 位似是相似的特殊情况.
知1-讲
感悟新知
特别提醒
●两个位似图形的位似中心有且只有一个.
●位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处.
感悟新知
知1-练
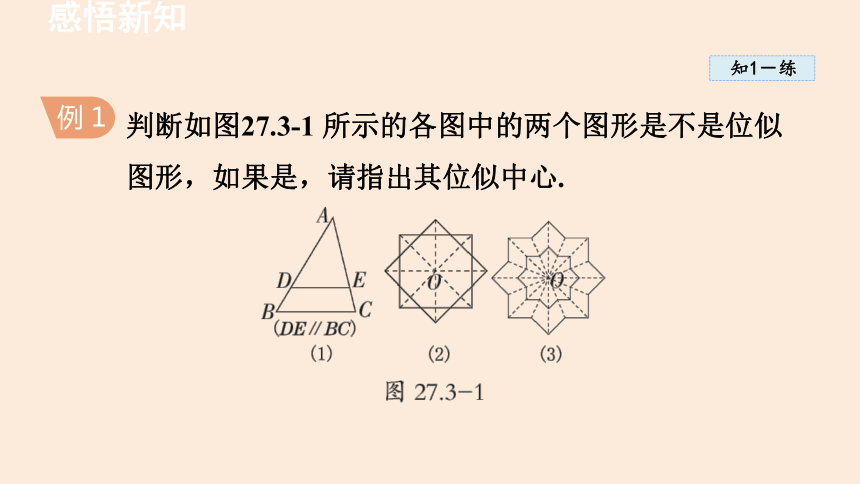
判断如图27.3-1 所示的各图中的两个图形是不是位似
图形,如果是,请指出其位似中心.
例 1
感悟新知
知1-练
解题秘方:紧扣“位似图形的定义”进行判断.
解:(1)是位似图形,位似中心为点A;
(2)不是位似图形;
(3)是位似图形,位似中心为点O.
感悟新知
知1-练
1-1. 为了增强视力保护意识,小红要在书房挂一张视力表,如图是视力表的一部分, 图中的类似“E”的图形均是相似图形,下面不是位似图形的是( )
A. ①和④
B. ②和③
C. ①和②
D. ②和④
B
知识点
位似图形的性质
知2-讲
感悟新知
2
位似图形具有的性质:
(1)位似图形每组对应顶点的连线必过位似中心.
(2)位似图形任意一组对应顶点到位似中心的距离之比等于相似比.
知2-讲
感悟新知
(3)位似图形的对应线段平行(或在同一条直线上),且对应线段之比相等.
(4)若两个图形位似,则这两个图形必相似,其周长比等于相似比,面积比等于相似比的平方.
知2-讲
感悟新知
特别解读
利用位似图形的性质可解决:
1. 多边形的放大或缩小;
2. 确定位似中心;
3. 求周长或面积.
感悟新知
知2-练
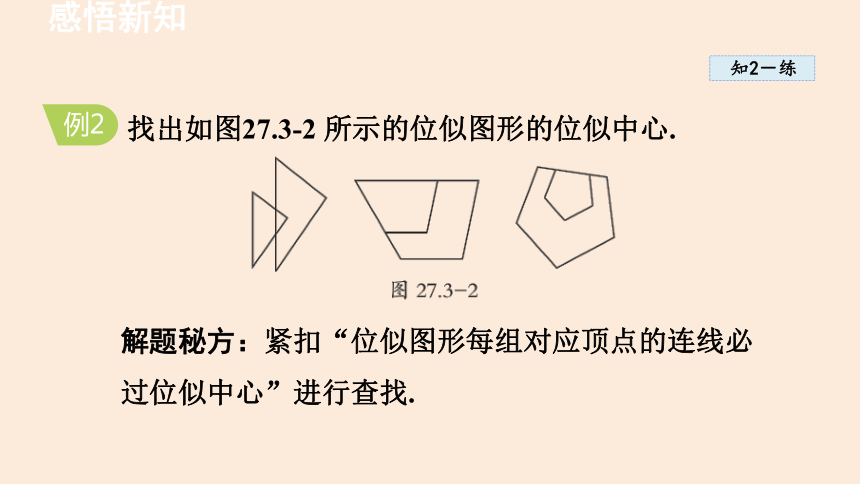
找出如图27.3-2 所示的位似图形的位似中心.
例2
解题秘方:紧扣“位似图形每组对应顶点的连线必过位似中心”进行查找.
知2-讲
感悟新知
解:如图27.3-3,点P1,P2,P3 即为所求的位似中心.
感悟新知
知2-练
2-1. 如图,网格中的两个三角形是位似图形,它们的位似中心是( )
A. 点A
B. 点B
C. 点C
D. 点D
D
感悟新知
知2-练
如图27.3-4,△ ABC 与△ A′B′C′关于点O 位似,
AO=3,A′O=6.
(1)若AC=5,求A′C′的长;
(2)若△ ABC 的面积为7,
求△ A′B′C′的面积.
解题秘方:紧扣位似图形相似比的性质进行计算.
例 3
知2-讲
感悟新知
解:(1)因为△ ABC 与△ A ′B ′C ′是位似图形,
AO ∶ A′O=3 ∶ 6=1 ∶ 2,
所以△ ABC ∽△ A′B′C′,且相似比为 ,
所以 即
所以A′C′=10.
知2-讲
感悟新知
(2)根据题意,得
即
所以S△ A′B′C′=7×4=28.
感悟新知
知2-练
3-2.[ 中考·重庆] 如图,△ ABC与△ DEF位似,点O 为位似中心,相似比为2 ∶ 3. 若△ ABC的周长为4,则△ DEF的周长是( )
A.4 B.6
C.9 D.16
C
知识点
位似图形的画法
知3-讲
感悟新知
3
画位似图形的步骤:
特别提醒
以一点为位似中心画位似图形时,符合要求的图形往往不唯一,一般情况下,同一个位似中心的两侧各有一个符合要求的图形.
知3-讲
感悟新知
(1)确定位似中心(位似中心可以在图形外部,也可以在图形内部,还可以在图形的边上或在某一个顶点处);
(2)分别连接位似中心和能代表原图的关键点,并延长;
(3)根据相似比,确定所画位似图形的关键点的位置;
(4)顺次连接所作各点,得到放大或缩小的图形.
注意:画位似图形时,要弄清相似比,即分清是已知图形
与新图形的相似比,还是新图形与已知图形的相似比.
感悟新知
知3-练
[开放题] 如图27.3-5,已知四边形ABCD,将四边形
ABCD 放大,使放大后的图形与原图形是位似图形,且放大后的图形与原图形对应线段的比为2 ∶ 1.
例4
解题秘方:紧扣“位似图形的定义和性质”,按画位似图形的步骤作图(画法不唯一).
感悟新知
知3-练
解:(画法不唯一)根据位似中心的不同位
置情况进行作图.
画法一:位似中心在四边形的顶点上,如图27.3-6,以点A 为位似中心,四边形AB1C1D1 就是所求作的图形.
感悟新知
知3-练
画法二:位似中心在四边形的边上,如图27.3-7,以
AD 边上一点为位似中心,四边形A1B1C1D1 就是所求作的图形.
感悟新知
知3-练
4-1. 如图, 在由边长为1 的小正方形组成的网格图中, 已知点O 及△ ABC 的顶点均为网格线的交点.
感悟新知
知3-练
(1)将△ ABC 绕着点B顺时针旋转90°,得到△ A1BC1,请在网格图中画出△ A1BC1.
解:如图所示,△A1BC1即为所求.
感悟新知
知3-练
(2)以点O 为位似中心, 将△ ABC 放大为原图形的3 倍, 得到△ A′B′C′,请在网格图中画出△ A′B′C′.
解:如图,△A′B′C′即为所求.
知识点
平面直角坐标系中的位似
知4-讲
感悟新知
4
1. 位似变换时对应点的坐标的变化规律:
特别提醒
●在平面直角坐标系中,以原点为位似中心,位似图形与原图形的相似比为k,那么当位似图形与原图形在原点的同侧时,原图形上的点(x,y) 对应的位似图形上的点的坐标为(kx,ky);当位似图形与原图形在原点的两侧时,原图形上的点(x,y) 对应的位似图形上的点的坐标为(-kx,-ky).
●当k>1 时,图形扩大为原来的k 倍;当0知4-讲
感悟新知
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
知4-讲
感悟新知
2. 位似变换与平移、轴对称、旋转三种变换的联系和区别:
(1)位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换.
(2)在直角坐标系中,把一个图形进行平移、轴对称、旋转或位似变换,其对应点的坐标都有各自的变化规律:
知4-讲
感悟新知
①平移变换是横坐标或纵坐标加上(或减去)平移的距离;
②在轴对称变换中,以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则纵坐标相等,横坐标互为相反数;
③在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
知4-讲
感悟新知
④在位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于变换后的图形与变换前的图形的相似比.
感悟新知
知4-练
如图27.3-8,已知O 是坐标原点,B,C 两点的坐标
分别为(3,-1),(2,1).
例 5
感悟新知
知4-练
(1)画出以点O 为位似中心,在y 轴的左侧将△ OBC 放大为原来的2 倍(即新图与原图的相似比为2)的位似图形△ OB′C′;
(2)分别写出B,C 两点的对应点B′,C′的坐标;
(3)如果△ OBC 内部一点M 的坐标为(x,y),试写出点M 的对应点M′的坐标.
感悟新知
知4-练
解题秘方:根据位似中心及相似比作图,再利用位似变换时对应点的坐标的变化规律求对应点的坐标.
方法点拨:位似变换作图的思路有两种: 一种是先求出变换后对应点的坐标,再描点画图;另一种是先根据对应边的比画出位似变换后的图形,再确定对应点的坐标.
感悟新知
知4-练
解:(1)如图27.3-9,延长BO 到点B′,使OB′=2OB;延长CO 到点C′,使OC′=2OC,连接B′C′,则△ OB′C′就是要画的图形.
感悟新知
知4-练
(2)点B′,C′的坐标分别为(-6,2),(-4,-2).
(3)点M(x,y)的对应点M′的坐标为(-2x, -2y).
感悟新知
知4-练
5-1. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ ABC 的三个顶点均在格点( 网格线的交点)上. 以原点O 为位似中心,
画△ A1B1C1, 使它与△ ABC 的
相似比为2,则点B 的对应点B1
的坐标是( )
感悟新知
知4-练
【答案】D
课堂小结
位似
位似图形
定义
性质
画法
坐标规律
27.3 位似
第27章 相似
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
位似图形的定义
位似图形的性质
位似图形的画法
平面直角坐标系中的位似
知识点
位似图形的定义
知1-讲
感悟新知
1
1. 定义:如果一个图形上的点A,B,…,P,…和另一个图形上的点A′,B′,…,P′,…分别对应,并且它们的连线AA′,BB′,…,PP′,…都经过同一点O,
…,那么这两个图形叫做位似图形,点O 是位似中心.
知1-讲
感悟新知
2. 位似与相似的关系:
(1)相似仅要求两个图形形状完全相同,而位似是在相似的基础上要求对应顶点的连线相交于一点.
(2)如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,因此, 位似是相似的特殊情况.
知1-讲
感悟新知
特别提醒
●两个位似图形的位似中心有且只有一个.
●位似中心可能位于两个位似图形的同侧,也可能位于两个位似图形之间,还可能位于两个位似图形的内部或边上或某一个顶点处.
感悟新知
知1-练
判断如图27.3-1 所示的各图中的两个图形是不是位似
图形,如果是,请指出其位似中心.
例 1
感悟新知
知1-练
解题秘方:紧扣“位似图形的定义”进行判断.
解:(1)是位似图形,位似中心为点A;
(2)不是位似图形;
(3)是位似图形,位似中心为点O.
感悟新知
知1-练
1-1. 为了增强视力保护意识,小红要在书房挂一张视力表,如图是视力表的一部分, 图中的类似“E”的图形均是相似图形,下面不是位似图形的是( )
A. ①和④
B. ②和③
C. ①和②
D. ②和④
B
知识点
位似图形的性质
知2-讲
感悟新知
2
位似图形具有的性质:
(1)位似图形每组对应顶点的连线必过位似中心.
(2)位似图形任意一组对应顶点到位似中心的距离之比等于相似比.
知2-讲
感悟新知
(3)位似图形的对应线段平行(或在同一条直线上),且对应线段之比相等.
(4)若两个图形位似,则这两个图形必相似,其周长比等于相似比,面积比等于相似比的平方.
知2-讲
感悟新知
特别解读
利用位似图形的性质可解决:
1. 多边形的放大或缩小;
2. 确定位似中心;
3. 求周长或面积.
感悟新知
知2-练
找出如图27.3-2 所示的位似图形的位似中心.
例2
解题秘方:紧扣“位似图形每组对应顶点的连线必过位似中心”进行查找.
知2-讲
感悟新知
解:如图27.3-3,点P1,P2,P3 即为所求的位似中心.
感悟新知
知2-练
2-1. 如图,网格中的两个三角形是位似图形,它们的位似中心是( )
A. 点A
B. 点B
C. 点C
D. 点D
D
感悟新知
知2-练
如图27.3-4,△ ABC 与△ A′B′C′关于点O 位似,
AO=3,A′O=6.
(1)若AC=5,求A′C′的长;
(2)若△ ABC 的面积为7,
求△ A′B′C′的面积.
解题秘方:紧扣位似图形相似比的性质进行计算.
例 3
知2-讲
感悟新知
解:(1)因为△ ABC 与△ A ′B ′C ′是位似图形,
AO ∶ A′O=3 ∶ 6=1 ∶ 2,
所以△ ABC ∽△ A′B′C′,且相似比为 ,
所以 即
所以A′C′=10.
知2-讲
感悟新知
(2)根据题意,得
即
所以S△ A′B′C′=7×4=28.
感悟新知
知2-练
3-2.[ 中考·重庆] 如图,△ ABC与△ DEF位似,点O 为位似中心,相似比为2 ∶ 3. 若△ ABC的周长为4,则△ DEF的周长是( )
A.4 B.6
C.9 D.16
C
知识点
位似图形的画法
知3-讲
感悟新知
3
画位似图形的步骤:
特别提醒
以一点为位似中心画位似图形时,符合要求的图形往往不唯一,一般情况下,同一个位似中心的两侧各有一个符合要求的图形.
知3-讲
感悟新知
(1)确定位似中心(位似中心可以在图形外部,也可以在图形内部,还可以在图形的边上或在某一个顶点处);
(2)分别连接位似中心和能代表原图的关键点,并延长;
(3)根据相似比,确定所画位似图形的关键点的位置;
(4)顺次连接所作各点,得到放大或缩小的图形.
注意:画位似图形时,要弄清相似比,即分清是已知图形
与新图形的相似比,还是新图形与已知图形的相似比.
感悟新知
知3-练
[开放题] 如图27.3-5,已知四边形ABCD,将四边形
ABCD 放大,使放大后的图形与原图形是位似图形,且放大后的图形与原图形对应线段的比为2 ∶ 1.
例4
解题秘方:紧扣“位似图形的定义和性质”,按画位似图形的步骤作图(画法不唯一).
感悟新知
知3-练
解:(画法不唯一)根据位似中心的不同位
置情况进行作图.
画法一:位似中心在四边形的顶点上,如图27.3-6,以点A 为位似中心,四边形AB1C1D1 就是所求作的图形.
感悟新知
知3-练
画法二:位似中心在四边形的边上,如图27.3-7,以
AD 边上一点为位似中心,四边形A1B1C1D1 就是所求作的图形.
感悟新知
知3-练
4-1. 如图, 在由边长为1 的小正方形组成的网格图中, 已知点O 及△ ABC 的顶点均为网格线的交点.
感悟新知
知3-练
(1)将△ ABC 绕着点B顺时针旋转90°,得到△ A1BC1,请在网格图中画出△ A1BC1.
解:如图所示,△A1BC1即为所求.
感悟新知
知3-练
(2)以点O 为位似中心, 将△ ABC 放大为原图形的3 倍, 得到△ A′B′C′,请在网格图中画出△ A′B′C′.
解:如图,△A′B′C′即为所求.
知识点
平面直角坐标系中的位似
知4-讲
感悟新知
4
1. 位似变换时对应点的坐标的变化规律:
特别提醒
●在平面直角坐标系中,以原点为位似中心,位似图形与原图形的相似比为k,那么当位似图形与原图形在原点的同侧时,原图形上的点(x,y) 对应的位似图形上的点的坐标为(kx,ky);当位似图形与原图形在原点的两侧时,原图形上的点(x,y) 对应的位似图形上的点的坐标为(-kx,-ky).
●当k>1 时,图形扩大为原来的k 倍;当0
感悟新知
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
知4-讲
感悟新知
2. 位似变换与平移、轴对称、旋转三种变换的联系和区别:
(1)位似、平移、轴对称、旋转都是图形变换的基本形式,它们的本质区别在于:平移、轴对称、旋转三种图形变换是全等变换,而位似变换是相似变换.
(2)在直角坐标系中,把一个图形进行平移、轴对称、旋转或位似变换,其对应点的坐标都有各自的变化规律:
知4-讲
感悟新知
①平移变换是横坐标或纵坐标加上(或减去)平移的距离;
②在轴对称变换中,以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数;以y轴为对称轴,则纵坐标相等,横坐标互为相反数;
③在旋转变换中,一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都分别互为相反数;
知4-讲
感悟新知
④在位似变换中,当以原点为位似中心时,变换后与变换前两个图形对应点的横坐标之比的绝对值、纵坐标之比的绝对值都等于变换后的图形与变换前的图形的相似比.
感悟新知
知4-练
如图27.3-8,已知O 是坐标原点,B,C 两点的坐标
分别为(3,-1),(2,1).
例 5
感悟新知
知4-练
(1)画出以点O 为位似中心,在y 轴的左侧将△ OBC 放大为原来的2 倍(即新图与原图的相似比为2)的位似图形△ OB′C′;
(2)分别写出B,C 两点的对应点B′,C′的坐标;
(3)如果△ OBC 内部一点M 的坐标为(x,y),试写出点M 的对应点M′的坐标.
感悟新知
知4-练
解题秘方:根据位似中心及相似比作图,再利用位似变换时对应点的坐标的变化规律求对应点的坐标.
方法点拨:位似变换作图的思路有两种: 一种是先求出变换后对应点的坐标,再描点画图;另一种是先根据对应边的比画出位似变换后的图形,再确定对应点的坐标.
感悟新知
知4-练
解:(1)如图27.3-9,延长BO 到点B′,使OB′=2OB;延长CO 到点C′,使OC′=2OC,连接B′C′,则△ OB′C′就是要画的图形.
感悟新知
知4-练
(2)点B′,C′的坐标分别为(-6,2),(-4,-2).
(3)点M(x,y)的对应点M′的坐标为(-2x, -2y).
感悟新知
知4-练
5-1. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ ABC 的三个顶点均在格点( 网格线的交点)上. 以原点O 为位似中心,
画△ A1B1C1, 使它与△ ABC 的
相似比为2,则点B 的对应点B1
的坐标是( )
感悟新知
知4-练
【答案】D
课堂小结
位似
位似图形
定义
性质
画法
坐标规律
