人教版数学九下28.2.1解直角三角形 课件(共31张PPT)
文档属性
| 名称 | 人教版数学九下28.2.1解直角三角形 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:40:24 | ||
图片预览










文档简介
(共31张PPT)
28.2 解直角三角形及其应用
第28章 锐角三角函数
28.2.1 解直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
解直角三角形的定义
直角三角形中的边角关系
知识点
解直角三角形的定义
知1-讲
感悟新知
1
定义:一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
知1-讲
感悟新知
特别提醒:(1)在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的三个未知元素(知二求三).
(2)一个直角三角形可解,则其面积可求. 但在一个解直角三角形的题中,如无特别说明,则不包括求面积.
深度理解
●已知两个角不能解直角三角形,因为只有角的条件,三角形边的大小不唯一,即有无数个三角形符合条件.
●已知一角一边时,角必须为锐角,因为若已知直角,则不能求解.
感悟新知
知1-练
根据下列所给条件解直角三角形,不能求解的是( )
①已知一直角边及其对角;②已知两锐角;③已知两直角边;
④已知斜边和一锐角;⑤已知一直角边和斜边.
A. ②③ B. ②④ C. 只有② D. ②④⑤
例 1
C
感悟新知
知1-练
解:①③④⑤能够求解;②不能求解.
解题秘方:紧扣解直角三角形中“知二求三”的特征进行解答.
特别提醒:解直角三角形时,求某些未知量的方法往往不唯一,选择关系式通常遵循以下原则:1. 尽量选择可以直接应用原始数据的关系式;2. 尽量选择便于计算的关系式;3. 能用乘法计算的要避免使用除法计算.
感悟新知
知1-练
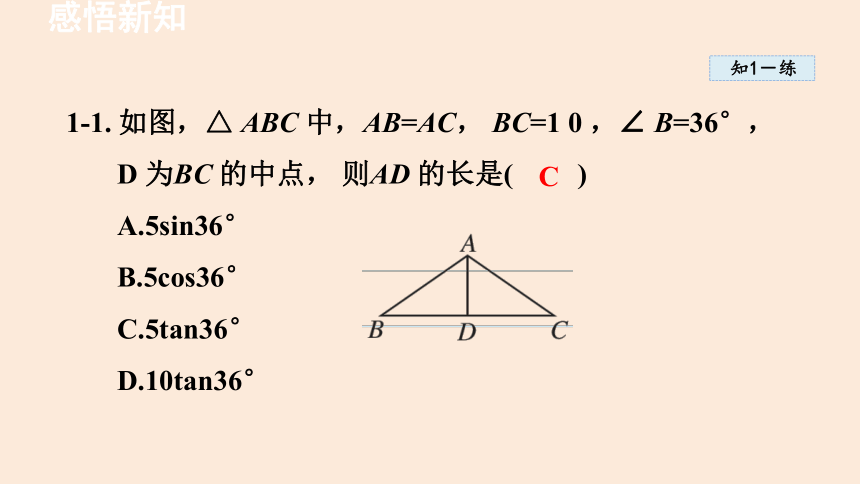
1-1. 如图,△ ABC 中,AB=AC, BC=1 0 ,∠ B=36°,D 为BC 的中点, 则AD 的长是( )
A.5sin36°
B.5cos36°
C.5tan36°
D.10tan36°
C
知识点
直角三角形中的边角关系
知2-讲
感悟新知
2
1. 直角三角形中的边角关系:在直角三角形ABC 中,∠ C 为直角,∠ A,∠ B,∠ C 所对的边分别为a,b,c,那么除直角∠ C外的五个元素之间有如下关系:
(1)三边之间的关系:a2+b2=c2(勾股定理).
(2)两锐角之间的关系:∠ A + ∠ B=90°
知2-讲
感悟新知
(3)边角之间的关系:
知2-讲
感悟新知
2. 运用关系式解直角三角形时,常常要用到以下变形:
(1)两锐角之间的关系:∠ A=90°-∠ B,∠ B=90° -∠ A;
(2)三边之间的关系:
(3)边角之间的关系:a=csin A,a=ccos B,a=btan A,b=csin B,b=ccos A,b=atan B.
知2-讲
感悟新知
活学巧记
口诀记忆法
有斜求对乘正弦,
有斜求邻乘余弦,
无斜求对乘正切.
知2-讲
感悟新知
“有斜求对乘正弦”的意思是:在一个直角三角形中,对一个锐角而言,如果已知斜边长,要求该锐角的对边,那么就用斜边长乘该锐角的正弦,其他的意思可类推.
感悟新知
知2-练
根据下列条件,解直角三角形:
(1)在Rt △ ABC 中,∠ C=90°,a=20,c=20 ;
(2)在Rt △ ABC 中,∠ C=90°,a=2 ,b=2.
例2
解题秘方:紧扣直角三角形的边角关系求解.
知2-讲
感悟新知
解:(1)在Rt △ ABC 中,∠ C=90°,
则sin A=
∴∠ A=45°,∴∠ B=90°-∠ A=45°,∴ b=a=20.
(2)在Rt △ ABC 中,∠ C=90°,
∵ a=2 ,b=2,∴ c=
∵ tan A= ∴∠ A=60°,
∴∠ B=90°-∠ A=90°-60°=30°.
感悟新知
知2-练
2-1. 如图, 在Rt △ABC 中, ∠ C=90 °,AC=2 ,BC=6, 解这个直角三角形.
感悟新知
知2-练
感悟新知
知2-练
根据下列条件,解直角三角形:
(1)在Rt △ ABC 中,∠ C=90°,∠ A=30°,b=12;
解题秘方:紧扣以下两种思路去求解
求边时,一般用未知边比已知边(或已知边比未知边),去找已知角的某一个锐角三角函数.
例 3
感悟新知
知2-练
解法提醒:
解直角三角形选择关系式常遵循的原则:
当已知或求解中有斜边时,优先考虑用正弦或余弦,无斜边时,就用正切;当所求的元素既可以用乘法又可以用除法求解时,优先考虑用乘法;在解题过程中,既可以用原始数据又可以用解题过程中得到的数据时,优先考虑用原始数据.
感悟新知
知2-练
解:在Rt △ ABC 中,∠ C=90°,∠ A=30°,
∴∠ B=90°-∠ A=60°.
感悟新知
知2-练
(2)在Rt △ ABC 中,∠ C=90°,∠ A=60°,c=6.
解题秘方:求角时,一般用已知边比已知边,去找未知角的某一个锐角三角函数.
感悟新知
知2-练
解法提醒:
解直角三角形选择关系式常遵循的原则:
当已知或求解中有斜边时,优先考虑用正弦或余弦,无斜边时,就用正切;当所求的元素既可以用乘法又可以用除法求解时,优先考虑用乘法;在解题过程中,既可以用原始数据又可以用解题过程中得到的数据时,优先考虑用原始数据.
感悟新知
知2-练
解:在Rt △ ABC 中,∠ C=90°,∠ A=60°,
∴∠ B=90°-∠ A=30°.
感悟新知
知2-练
3-1. 在Rt △ ABC 中,∠ C=90°,根据下列条件解直角三角形:
(1)c=30,b=20;
感悟新知
知2-练
(2)∠ B=72°,c=14;
感悟新知
知2-练
(3)∠ B=30°,a= .
感悟新知
知2-练
如图28.2-1,在△ ABC 中,AB=1,AC= ,sin B=
,求BC 的长.
例4
解题秘方:紧扣“化斜为直法”,通过作高把斜三角形转化为两个直角三角形求解.
知2-讲
感悟新知
教你一招:构造直角三角形解非直角三角形问题的方法
通过作垂线(高),将斜三角形分割成两个直角三角形,然后利用解直角三角形求边或角. 在作垂线时,要充分利用已知条件, 一般在等腰三角形中作底边上的高,或过特殊角的一边上的点作这个角的另一边的垂线,从而构造含特殊角的直角三角形,再利用解直角三角形的相关知识求解.
知2-讲
感悟新知
解:如图28.2-1 所示,过点A 作AE ⊥ BC,垂足为点E.
在Rt △ ABE 中,∵ sin B= ,AB=1,
∴ AE= ,∴ EB=
在Rt △ ACE 中,AC=
∴ CE= .
∴ BC=BE+CE=
感悟新知
知2-练
4-1. 在△ ABC 中,∠ B=45°,∠ C=60°,BC 边上的高AD=3,则BC 的长为( )
A.3+3
B.3+
C.2+
D. 3 +
B
感悟新知
知2-练
4-2. 如图,在△ ABC中,∠ A=30°,∠ B=45°,AC=6,则△ ABC 的周长为______________ .
课堂小结
解直角三角形
三边关系
边角关系
解直
角三
角形
定义
条件
两锐角关系
依据
28.2 解直角三角形及其应用
第28章 锐角三角函数
28.2.1 解直角三角形
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
解直角三角形的定义
直角三角形中的边角关系
知识点
解直角三角形的定义
知1-讲
感悟新知
1
定义:一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
知1-讲
感悟新知
特别提醒:(1)在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的三个未知元素(知二求三).
(2)一个直角三角形可解,则其面积可求. 但在一个解直角三角形的题中,如无特别说明,则不包括求面积.
深度理解
●已知两个角不能解直角三角形,因为只有角的条件,三角形边的大小不唯一,即有无数个三角形符合条件.
●已知一角一边时,角必须为锐角,因为若已知直角,则不能求解.
感悟新知
知1-练
根据下列所给条件解直角三角形,不能求解的是( )
①已知一直角边及其对角;②已知两锐角;③已知两直角边;
④已知斜边和一锐角;⑤已知一直角边和斜边.
A. ②③ B. ②④ C. 只有② D. ②④⑤
例 1
C
感悟新知
知1-练
解:①③④⑤能够求解;②不能求解.
解题秘方:紧扣解直角三角形中“知二求三”的特征进行解答.
特别提醒:解直角三角形时,求某些未知量的方法往往不唯一,选择关系式通常遵循以下原则:1. 尽量选择可以直接应用原始数据的关系式;2. 尽量选择便于计算的关系式;3. 能用乘法计算的要避免使用除法计算.
感悟新知
知1-练
1-1. 如图,△ ABC 中,AB=AC, BC=1 0 ,∠ B=36°,D 为BC 的中点, 则AD 的长是( )
A.5sin36°
B.5cos36°
C.5tan36°
D.10tan36°
C
知识点
直角三角形中的边角关系
知2-讲
感悟新知
2
1. 直角三角形中的边角关系:在直角三角形ABC 中,∠ C 为直角,∠ A,∠ B,∠ C 所对的边分别为a,b,c,那么除直角∠ C外的五个元素之间有如下关系:
(1)三边之间的关系:a2+b2=c2(勾股定理).
(2)两锐角之间的关系:∠ A + ∠ B=90°
知2-讲
感悟新知
(3)边角之间的关系:
知2-讲
感悟新知
2. 运用关系式解直角三角形时,常常要用到以下变形:
(1)两锐角之间的关系:∠ A=90°-∠ B,∠ B=90° -∠ A;
(2)三边之间的关系:
(3)边角之间的关系:a=csin A,a=ccos B,a=btan A,b=csin B,b=ccos A,b=atan B.
知2-讲
感悟新知
活学巧记
口诀记忆法
有斜求对乘正弦,
有斜求邻乘余弦,
无斜求对乘正切.
知2-讲
感悟新知
“有斜求对乘正弦”的意思是:在一个直角三角形中,对一个锐角而言,如果已知斜边长,要求该锐角的对边,那么就用斜边长乘该锐角的正弦,其他的意思可类推.
感悟新知
知2-练
根据下列条件,解直角三角形:
(1)在Rt △ ABC 中,∠ C=90°,a=20,c=20 ;
(2)在Rt △ ABC 中,∠ C=90°,a=2 ,b=2.
例2
解题秘方:紧扣直角三角形的边角关系求解.
知2-讲
感悟新知
解:(1)在Rt △ ABC 中,∠ C=90°,
则sin A=
∴∠ A=45°,∴∠ B=90°-∠ A=45°,∴ b=a=20.
(2)在Rt △ ABC 中,∠ C=90°,
∵ a=2 ,b=2,∴ c=
∵ tan A= ∴∠ A=60°,
∴∠ B=90°-∠ A=90°-60°=30°.
感悟新知
知2-练
2-1. 如图, 在Rt △ABC 中, ∠ C=90 °,AC=2 ,BC=6, 解这个直角三角形.
感悟新知
知2-练
感悟新知
知2-练
根据下列条件,解直角三角形:
(1)在Rt △ ABC 中,∠ C=90°,∠ A=30°,b=12;
解题秘方:紧扣以下两种思路去求解
求边时,一般用未知边比已知边(或已知边比未知边),去找已知角的某一个锐角三角函数.
例 3
感悟新知
知2-练
解法提醒:
解直角三角形选择关系式常遵循的原则:
当已知或求解中有斜边时,优先考虑用正弦或余弦,无斜边时,就用正切;当所求的元素既可以用乘法又可以用除法求解时,优先考虑用乘法;在解题过程中,既可以用原始数据又可以用解题过程中得到的数据时,优先考虑用原始数据.
感悟新知
知2-练
解:在Rt △ ABC 中,∠ C=90°,∠ A=30°,
∴∠ B=90°-∠ A=60°.
感悟新知
知2-练
(2)在Rt △ ABC 中,∠ C=90°,∠ A=60°,c=6.
解题秘方:求角时,一般用已知边比已知边,去找未知角的某一个锐角三角函数.
感悟新知
知2-练
解法提醒:
解直角三角形选择关系式常遵循的原则:
当已知或求解中有斜边时,优先考虑用正弦或余弦,无斜边时,就用正切;当所求的元素既可以用乘法又可以用除法求解时,优先考虑用乘法;在解题过程中,既可以用原始数据又可以用解题过程中得到的数据时,优先考虑用原始数据.
感悟新知
知2-练
解:在Rt △ ABC 中,∠ C=90°,∠ A=60°,
∴∠ B=90°-∠ A=30°.
感悟新知
知2-练
3-1. 在Rt △ ABC 中,∠ C=90°,根据下列条件解直角三角形:
(1)c=30,b=20;
感悟新知
知2-练
(2)∠ B=72°,c=14;
感悟新知
知2-练
(3)∠ B=30°,a= .
感悟新知
知2-练
如图28.2-1,在△ ABC 中,AB=1,AC= ,sin B=
,求BC 的长.
例4
解题秘方:紧扣“化斜为直法”,通过作高把斜三角形转化为两个直角三角形求解.
知2-讲
感悟新知
教你一招:构造直角三角形解非直角三角形问题的方法
通过作垂线(高),将斜三角形分割成两个直角三角形,然后利用解直角三角形求边或角. 在作垂线时,要充分利用已知条件, 一般在等腰三角形中作底边上的高,或过特殊角的一边上的点作这个角的另一边的垂线,从而构造含特殊角的直角三角形,再利用解直角三角形的相关知识求解.
知2-讲
感悟新知
解:如图28.2-1 所示,过点A 作AE ⊥ BC,垂足为点E.
在Rt △ ABE 中,∵ sin B= ,AB=1,
∴ AE= ,∴ EB=
在Rt △ ACE 中,AC=
∴ CE= .
∴ BC=BE+CE=
感悟新知
知2-练
4-1. 在△ ABC 中,∠ B=45°,∠ C=60°,BC 边上的高AD=3,则BC 的长为( )
A.3+3
B.3+
C.2+
D. 3 +
B
感悟新知
知2-练
4-2. 如图,在△ ABC中,∠ A=30°,∠ B=45°,AC=6,则△ ABC 的周长为______________ .
课堂小结
解直角三角形
三边关系
边角关系
解直
角三
角形
定义
条件
两锐角关系
依据
