人教版数学九下28.2.2应用举例 课件(共46张PPT)
文档属性
| 名称 | 人教版数学九下28.2.2应用举例 课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:41:39 | ||
图片预览









文档简介
(共46张PPT)
28.2 解直角三角形及其应用
第28章 锐角三角函数
28.2.2 应用举例
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
解直角三角形在实际中的应用
解直角三角形在解仰角和俯角中的应用
解直角三角形在解方向角中的应用
解直角三角形解坡角、坡度的应用
知识点
解直角三角形在实际中的应用
知1-讲
感悟新知
1
1. 利用解直角三角形解决实际问题的一般步骤
(1)画出平面图形,将实际问题抽象为数学问题,转化为解直角三角形的问题;
(2)根据已知条件的特点,灵活选用锐角三角函数等知识解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知1-讲
感悟新知
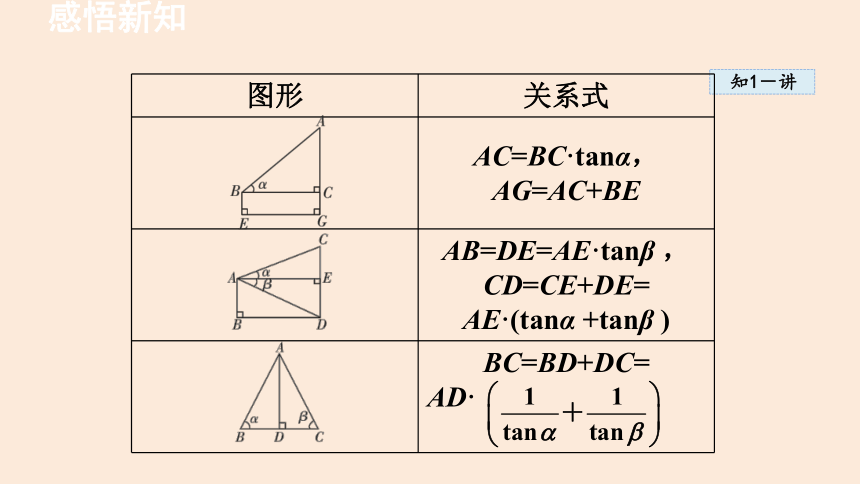
2. 解决实际问题时,常见的基本图形及相应的关系式如下表所示:
知1-讲
感悟新知
图形 关系式
AC=BC·tanα,
AG=AC+BE
AB=DE=AE·tanβ ,
CD=CE+DE=
AE·(tanα +tanβ )
BC=BD+DC=
AD·
知1-讲
感悟新知
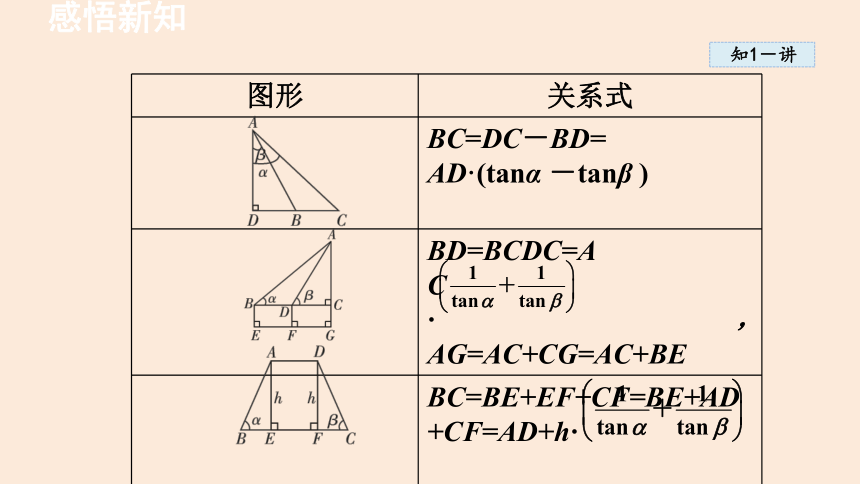
图形 关系式
BC=DC-BD=
AD·(tanα -tanβ )
BD=BCDC=AC· ,AG=AC+CG=AC+BE
BC=BE+EF+CF=BE+AD+CF=AD+h·
知1-讲
感悟新知
特别提醒
1. 当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
2. 在解直角三角形时,若相关的角不是直角三角形的内角,应利用平行线的性质或互余、互补的角的性质将其转化为直角三角形的内角,再利用解直角三角形的知识求解.
知1-讲
感悟新知
3. 问题中有两个或两个以上的直角三角形,当其中一个直角三角形不能求解时,可考虑分别由两个直角三角形找出含有相同未知元素的关系式,运用方程求解.
感悟新知
知1-练
如图28.2-12 所示,某居民楼Ⅰ高20 m,窗户朝南,该楼内一楼住户的窗台离地面的距离CM 为2 m,窗户CD 高1.8 m. 现计划在楼Ⅰ的正南方距楼Ⅰ 30 m 处新建一居民楼Ⅱ . 当正午时刻太阳光线
与地面成30°角时,要使楼Ⅱ的影
子不影响楼Ⅰ所有住户的采光,新
建楼Ⅱ最高只能建多少米?
例 1
感悟新知
知1-练
解题秘方:将实际应用问题建模成解直角三角形问题.
解:设正午时刻,太阳光线正好照在楼Ⅰ一楼的窗台处,此时新建居民楼Ⅱ高EG=x m,如图28.2-12 所示,
感悟新知
知1-练
过点C 作CF ⊥ EG 于点F,则FG=CM=2 m.
在Rt△ ECF中,EF = (x-2) m , FC = 30m ,
∠ ECF=30°,
∴ tan 30°= ,∴ x=10 +2.
答:新建楼Ⅱ最高只能建(10 +2)m.
感悟新知
知1-练
1-1. [中考· 十堰]如图, 小明利用一个锐角是30 ° 的三角尺测量操场旗杆的高度,已知他与旗杆之间的水平距离BC 为15 m,AB 为1.5 m( 即小明的眼睛与地面的距离),那么旗杆的高度是( )
D
感悟新知
知1-练
某工程队承包了一段铁路的施工,该铁路要经过某一隧道,如图28.2-13,已知隧道口分别为D,E. 为了如期完工,需测量出DE 的长度,为此,该工程队在山的一侧选取适当的点C,测得BC=200 m,∠ABC=105°,∠ C=45°,AD=18 m,BE=32 m,且A,D,E,
B 在同一条直线上,已知该工程限定时
间为10 天,该工程队平均每天至少需要
施工多少米?
例2
感悟新知
知1-练
解题秘方:在建立的非直角三角形模型中,用“化斜为直法”解含公共直角边的直角三角形问题.
解:如图28.2-13 所示,过点B 作BF ⊥ AC 于点F.
∵∠ ABC=105°,∠ C=45°,
∴∠ A=30°,△ BFC 为等腰直角三角形.
感悟新知
知1-练
在Rt △ BFC 中,∵ cos C= ,
∴ BF=FC=BC·cos C=200× =100 (m).
在Rt △ AFB 中,∵∠ A=30°,∴ AB=2BF=200 m.
又∵ AD=18 m,BE=32 m,
∴ DE=AB-AD-BE=200 -18 -32 =150 (m).
∵ 150 ÷10=15 (m),
∴该工程队平均每天至少需要施工15 m.
感悟新知
知1-练
2-1. 如图,要测量小河两岸相对的两点P,A 的距离, 可以在小河边取PA 的垂线PB 上的一点C, 测得PC=100 米,∠ PCA=35°,则小河宽PA 等于( )
A.100sin35°米
B.100sin55°米
C.100tan35°米
D.100tan55°米
C
知识点
解直角三角形在解仰角和俯角中的应用
知2-讲
感悟新知
2
1. 仰角和俯角的定义:
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.
特别提醒
●仰角和俯角是视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”.
●当实际问题中遇到仰角或俯角时,要放在直角三角形中或转化到直角三角形中,注意确定水平线.
知2-讲
感悟新知
2. 示图(如图28.2-14):
感悟新知
知2-练
如图28.2-15,在数学活动课中,小敏为了测量校园
内旗杆CD 的高度,先在教学楼的底端A 处,
观测到旗杆顶端C 的仰角∠ CAD=60°,
然后爬到教学楼上的B 处,观测到旗
杆底端D 的俯角是30°,已知教学
楼AB 高4 米.
例 3
感悟新知
知2-练
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD 的高度.
解题秘方:将实际问题转化为解直角三角形问题求解.
知2-讲
感悟新知
解:(1)∵在教学楼上的B 处观测旗杆底端D 的俯角是30°,∴∠ ADB=30° .
在Rt △ ABD 中,
∵∠ BAD=90°,∠ ADB=30°,AB=4 米,
∴教学楼与旗杆的水平距离AD 是4 米.
知2-讲
感悟新知
(2)在Rt △ ACD 中,
∵∠ ADC=90°,∠ CAD=60°,AD=4 米,
∴ CD=AD·tan60° =4 × =12(米).
∴旗杆CD 的高度是12 米.
感悟新知
知2-练
3-1. [中考.宿迁]某学习小组在教学楼AB的顶部观测信号塔CD底部的俯角为30°,信号塔顶部的仰角为45°.
已知教学楼AB的高度为20 m,求信号
塔的高度(计算结 果保留根号) .
感悟新知
知2-练
解:如图,过点A作AE⊥CD ,垂足为E,
由题意得AB= DE=20 m,
在Rt△ADE中,∠EAD=30,
∴
感悟新知
知2-练
在Rt△AEC中, ∠CAE=45°,
CE=AE · tan 45°=20 ×1 =20 (m),
∴CD=CE+DE= (20 +20 )m,
即信号塔的高度为(20 +20 )m.
知识点
解直角三角形在解方向角中的应用
知3-讲
感悟新知
3
1. 方向角的定义:
指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.
特别警示:方向角和方位角不同,方位角是指从某点的指北方向线起,按顺时针方向到目标方向线之间的水平夹角,变化范围为0°~360°,而方向角的变化范围是0°~90° .
知3-讲
感悟新知
2. 示图:
如图28.2-16 所示, 目标方向线OA,OB,OC 的方向角分别可以表示为北偏东30°、南偏东45°、北偏西30°,其中南偏东45°习惯上又叫做东南方向,北偏东45°习惯上又叫做东北方向,北偏西45°习惯上又叫做西北方向,南偏西45°习惯上又叫做西南方向.
知3-讲
感悟新知
特别提醒
1. 解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.
2. 观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助此性质进行角度转换.
感悟新知
知3-练
为了维护海洋权益,国家海洋局加大了在南海的巡逻
力度,一天,我国两艘海警船刚好在我国某岛东西海岸线上的A,B 两处巡逻,同时发现一艘不明国籍的船只停在C 处海域,如图28.2-17 所示,AB=60( + )海里,在B 处测得C 在北偏东45°的方向上,在A 处测得C
在北偏西30°的方向上,在海岸线AB 上
有一灯塔D,测得AD=120( – )海里.
例4
感悟新知
知3-练
(1)分别求出A 与C 及B 与C 的距离;(结果保留根号)
(2)已知在灯塔D 周围100 海里范围内有暗礁群,在A 处的海警船沿AC 前往C 处盘查,途中有无触礁的危险?(参考数据: ≈ 1.41, ≈ 1.73, ≈ 2.45)
解题秘方:建立数学模型后,用“化斜为直法”,将斜三角形问题转化为直角三角形问题求解.
感悟新知
知3-练
解:(1)如图28.2-17,过点C 作CE ⊥ AB 于点E,可得
∠ ACE=30°,∠ BCE=45°,设AE=x 海里,
在Rt △ ACE 中,CE= x 海里,AC=2x 海里,
在Rt △ BCE 中,BE=CE= x 海里,BC= x 海里.
∵ AB=AE+BE,∴ x+ 3 x=60( + ),
解得x=60 . ∴ AC=120 海里,BC=120 海里.
感悟新知
知3-练
(2)如图28.2-17, 过点D 作DF ⊥ AC 于点F, 可得
∠ DAF=60° .
在Rt △ AFD 中,∵ DF=DA·sin60° = DA,
∴DF= ×120( - )=60(3 - )≈ 106.8(海
里)>100 海里.
∴途中无触礁的危险.
感悟新知
知3-练
4-1.[中考.安徽]如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°
方向上.求A,B两点间的距离.(参考
数据:sin37°≈0.60, cos37°≈0.80,
tan37°≈0.75)
感悟新知
知3-练
解:如图,∵CE∥AD,
∴∠A=∠ECA=37°,
∴∠CBD=∠A+∠ADB=
37°+53°=90°,
∴∠CBD°=90°,
感悟新知
知3-练
在Rt△BCD中,∠BDC=90°-53°=37°,
CD=90米,cos∠BDC= ,
∴BD=CD·cos37°≈90×0.80=72(米),
在Rt△ABD中,∠A=37°,BD ≈72(米),
答:A、B两点间的距离约为96米.
知识点
解直角三角形解坡角、坡度的应用
知4-讲
感悟新知
4
1. 坡角与坡度(坡比)的定义:
特别提醒
1. 坡度是两条线段的比值,不是度数.
2. 表示坡度时,通常把比的前项取作1,后项可以是小数.
知4-讲
感悟新知
(1)坡角:坡面与水平面所成的夹角,如图28.2-18 中的α .
(2)坡度(坡比):我们通常把坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)(如图28.2-18 所示),坡度(坡比)也可写成i = h∶l的形式,在实际应用中常表示成1∶x的形式.
知4-讲
感悟新知
2. 坡度与坡角的关系:
=tanα ,即坡度是坡角的正切值,坡角越大,坡度也就越大.
感悟新知
知4-练
如图28.2-19,李明在大楼30 m 高(即PH=30 m)的窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60° . 已知该山坡的坡度i 为1 ∶ ,点P,H,B,C,A 在同一个平面内,
点H,B,C 在同一条直线上,
且PH ⊥ HC.
例 5
感悟新知
知4-练
(1)山坡坡角的度数等于 ______°;
(2)求A,B 两点间的距离(结果精确到0.1 m,参考数据:
≈ 1.732).
解题秘方:将分散的条件集中到△ ABP 中求解.
30
∵山坡坡角为∠ ABC,
坡度i=1 ∶ ,
∴ tan ∠ ABC=
∴∠ ABC=30° .
感悟新知
知4-练
解:由题意,得∠ PBH=60°,
∠ APB=60° -15° =45° .
∵∠ ABC=30°,∴∠ ABP=90° .
∴∠ BAP=45°,∴ PB=AB.
在Rt △ PHB 中,
∴ AB=PB=20 ≈ 34.6m.
∴ A,B 两点间的距离约为34.6 m.
感悟新知
知4-练
5-1. [中考· 益阳]沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD, 高DH=12 米,斜坡CD 的坡度i=1 ∶ 1. 此处大堤的正上方有高压电线穿过,PD 表示高压线上的点与堤面AD 的最近距离(P,D,H 在同一直线上),在点C 处测得∠ DCP=26° .
感悟新知
知4-练
(1)求斜坡CD 的坡角α ;
感悟新知
知4-练
(2)电力部门要求此处高压线离堤面AD 的安全距离不低于18 米,请问此次改造是否符合电力部门的安全要求?(参考数据:sin 26°≈0.44,tan 26°≈ 0.49,sin 71 ° ≈ 0.95,tan71°≈ 2.90)
感悟新知
知4-练
课堂小结
应用举例
仰角和俯角问题
坡角和坡度问题
解直角三角形的应用类型
方向角问题
一般步骤
一般测量问题
28.2 解直角三角形及其应用
第28章 锐角三角函数
28.2.2 应用举例
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
解直角三角形在实际中的应用
解直角三角形在解仰角和俯角中的应用
解直角三角形在解方向角中的应用
解直角三角形解坡角、坡度的应用
知识点
解直角三角形在实际中的应用
知1-讲
感悟新知
1
1. 利用解直角三角形解决实际问题的一般步骤
(1)画出平面图形,将实际问题抽象为数学问题,转化为解直角三角形的问题;
(2)根据已知条件的特点,灵活选用锐角三角函数等知识解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
知1-讲
感悟新知
2. 解决实际问题时,常见的基本图形及相应的关系式如下表所示:
知1-讲
感悟新知
图形 关系式
AC=BC·tanα,
AG=AC+BE
AB=DE=AE·tanβ ,
CD=CE+DE=
AE·(tanα +tanβ )
BC=BD+DC=
AD·
知1-讲
感悟新知
图形 关系式
BC=DC-BD=
AD·(tanα -tanβ )
BD=BCDC=AC· ,AG=AC+CG=AC+BE
BC=BE+EF+CF=BE+AD+CF=AD+h·
知1-讲
感悟新知
特别提醒
1. 当实际问题中涉及的图形可以直接转化为直角三角形时,可利用解直角三角形的知识直接求解.
2. 在解直角三角形时,若相关的角不是直角三角形的内角,应利用平行线的性质或互余、互补的角的性质将其转化为直角三角形的内角,再利用解直角三角形的知识求解.
知1-讲
感悟新知
3. 问题中有两个或两个以上的直角三角形,当其中一个直角三角形不能求解时,可考虑分别由两个直角三角形找出含有相同未知元素的关系式,运用方程求解.
感悟新知
知1-练
如图28.2-12 所示,某居民楼Ⅰ高20 m,窗户朝南,该楼内一楼住户的窗台离地面的距离CM 为2 m,窗户CD 高1.8 m. 现计划在楼Ⅰ的正南方距楼Ⅰ 30 m 处新建一居民楼Ⅱ . 当正午时刻太阳光线
与地面成30°角时,要使楼Ⅱ的影
子不影响楼Ⅰ所有住户的采光,新
建楼Ⅱ最高只能建多少米?
例 1
感悟新知
知1-练
解题秘方:将实际应用问题建模成解直角三角形问题.
解:设正午时刻,太阳光线正好照在楼Ⅰ一楼的窗台处,此时新建居民楼Ⅱ高EG=x m,如图28.2-12 所示,
感悟新知
知1-练
过点C 作CF ⊥ EG 于点F,则FG=CM=2 m.
在Rt△ ECF中,EF = (x-2) m , FC = 30m ,
∠ ECF=30°,
∴ tan 30°= ,∴ x=10 +2.
答:新建楼Ⅱ最高只能建(10 +2)m.
感悟新知
知1-练
1-1. [中考· 十堰]如图, 小明利用一个锐角是30 ° 的三角尺测量操场旗杆的高度,已知他与旗杆之间的水平距离BC 为15 m,AB 为1.5 m( 即小明的眼睛与地面的距离),那么旗杆的高度是( )
D
感悟新知
知1-练
某工程队承包了一段铁路的施工,该铁路要经过某一隧道,如图28.2-13,已知隧道口分别为D,E. 为了如期完工,需测量出DE 的长度,为此,该工程队在山的一侧选取适当的点C,测得BC=200 m,∠ABC=105°,∠ C=45°,AD=18 m,BE=32 m,且A,D,E,
B 在同一条直线上,已知该工程限定时
间为10 天,该工程队平均每天至少需要
施工多少米?
例2
感悟新知
知1-练
解题秘方:在建立的非直角三角形模型中,用“化斜为直法”解含公共直角边的直角三角形问题.
解:如图28.2-13 所示,过点B 作BF ⊥ AC 于点F.
∵∠ ABC=105°,∠ C=45°,
∴∠ A=30°,△ BFC 为等腰直角三角形.
感悟新知
知1-练
在Rt △ BFC 中,∵ cos C= ,
∴ BF=FC=BC·cos C=200× =100 (m).
在Rt △ AFB 中,∵∠ A=30°,∴ AB=2BF=200 m.
又∵ AD=18 m,BE=32 m,
∴ DE=AB-AD-BE=200 -18 -32 =150 (m).
∵ 150 ÷10=15 (m),
∴该工程队平均每天至少需要施工15 m.
感悟新知
知1-练
2-1. 如图,要测量小河两岸相对的两点P,A 的距离, 可以在小河边取PA 的垂线PB 上的一点C, 测得PC=100 米,∠ PCA=35°,则小河宽PA 等于( )
A.100sin35°米
B.100sin55°米
C.100tan35°米
D.100tan55°米
C
知识点
解直角三角形在解仰角和俯角中的应用
知2-讲
感悟新知
2
1. 仰角和俯角的定义:
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.
特别提醒
●仰角和俯角是视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”.
●当实际问题中遇到仰角或俯角时,要放在直角三角形中或转化到直角三角形中,注意确定水平线.
知2-讲
感悟新知
2. 示图(如图28.2-14):
感悟新知
知2-练
如图28.2-15,在数学活动课中,小敏为了测量校园
内旗杆CD 的高度,先在教学楼的底端A 处,
观测到旗杆顶端C 的仰角∠ CAD=60°,
然后爬到教学楼上的B 处,观测到旗
杆底端D 的俯角是30°,已知教学
楼AB 高4 米.
例 3
感悟新知
知2-练
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD 的高度.
解题秘方:将实际问题转化为解直角三角形问题求解.
知2-讲
感悟新知
解:(1)∵在教学楼上的B 处观测旗杆底端D 的俯角是30°,∴∠ ADB=30° .
在Rt △ ABD 中,
∵∠ BAD=90°,∠ ADB=30°,AB=4 米,
∴教学楼与旗杆的水平距离AD 是4 米.
知2-讲
感悟新知
(2)在Rt △ ACD 中,
∵∠ ADC=90°,∠ CAD=60°,AD=4 米,
∴ CD=AD·tan60° =4 × =12(米).
∴旗杆CD 的高度是12 米.
感悟新知
知2-练
3-1. [中考.宿迁]某学习小组在教学楼AB的顶部观测信号塔CD底部的俯角为30°,信号塔顶部的仰角为45°.
已知教学楼AB的高度为20 m,求信号
塔的高度(计算结 果保留根号) .
感悟新知
知2-练
解:如图,过点A作AE⊥CD ,垂足为E,
由题意得AB= DE=20 m,
在Rt△ADE中,∠EAD=30,
∴
感悟新知
知2-练
在Rt△AEC中, ∠CAE=45°,
CE=AE · tan 45°=20 ×1 =20 (m),
∴CD=CE+DE= (20 +20 )m,
即信号塔的高度为(20 +20 )m.
知识点
解直角三角形在解方向角中的应用
知3-讲
感悟新知
3
1. 方向角的定义:
指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.
特别警示:方向角和方位角不同,方位角是指从某点的指北方向线起,按顺时针方向到目标方向线之间的水平夹角,变化范围为0°~360°,而方向角的变化范围是0°~90° .
知3-讲
感悟新知
2. 示图:
如图28.2-16 所示, 目标方向线OA,OB,OC 的方向角分别可以表示为北偏东30°、南偏东45°、北偏西30°,其中南偏东45°习惯上又叫做东南方向,北偏东45°习惯上又叫做东北方向,北偏西45°习惯上又叫做西北方向,南偏西45°习惯上又叫做西南方向.
知3-讲
感悟新知
特别提醒
1. 解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.
2. 观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助此性质进行角度转换.
感悟新知
知3-练
为了维护海洋权益,国家海洋局加大了在南海的巡逻
力度,一天,我国两艘海警船刚好在我国某岛东西海岸线上的A,B 两处巡逻,同时发现一艘不明国籍的船只停在C 处海域,如图28.2-17 所示,AB=60( + )海里,在B 处测得C 在北偏东45°的方向上,在A 处测得C
在北偏西30°的方向上,在海岸线AB 上
有一灯塔D,测得AD=120( – )海里.
例4
感悟新知
知3-练
(1)分别求出A 与C 及B 与C 的距离;(结果保留根号)
(2)已知在灯塔D 周围100 海里范围内有暗礁群,在A 处的海警船沿AC 前往C 处盘查,途中有无触礁的危险?(参考数据: ≈ 1.41, ≈ 1.73, ≈ 2.45)
解题秘方:建立数学模型后,用“化斜为直法”,将斜三角形问题转化为直角三角形问题求解.
感悟新知
知3-练
解:(1)如图28.2-17,过点C 作CE ⊥ AB 于点E,可得
∠ ACE=30°,∠ BCE=45°,设AE=x 海里,
在Rt △ ACE 中,CE= x 海里,AC=2x 海里,
在Rt △ BCE 中,BE=CE= x 海里,BC= x 海里.
∵ AB=AE+BE,∴ x+ 3 x=60( + ),
解得x=60 . ∴ AC=120 海里,BC=120 海里.
感悟新知
知3-练
(2)如图28.2-17, 过点D 作DF ⊥ AC 于点F, 可得
∠ DAF=60° .
在Rt △ AFD 中,∵ DF=DA·sin60° = DA,
∴DF= ×120( - )=60(3 - )≈ 106.8(海
里)>100 海里.
∴途中无触礁的危险.
感悟新知
知3-练
4-1.[中考.安徽]如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°
方向上.求A,B两点间的距离.(参考
数据:sin37°≈0.60, cos37°≈0.80,
tan37°≈0.75)
感悟新知
知3-练
解:如图,∵CE∥AD,
∴∠A=∠ECA=37°,
∴∠CBD=∠A+∠ADB=
37°+53°=90°,
∴∠CBD°=90°,
感悟新知
知3-练
在Rt△BCD中,∠BDC=90°-53°=37°,
CD=90米,cos∠BDC= ,
∴BD=CD·cos37°≈90×0.80=72(米),
在Rt△ABD中,∠A=37°,BD ≈72(米),
答:A、B两点间的距离约为96米.
知识点
解直角三角形解坡角、坡度的应用
知4-讲
感悟新知
4
1. 坡角与坡度(坡比)的定义:
特别提醒
1. 坡度是两条线段的比值,不是度数.
2. 表示坡度时,通常把比的前项取作1,后项可以是小数.
知4-讲
感悟新知
(1)坡角:坡面与水平面所成的夹角,如图28.2-18 中的α .
(2)坡度(坡比):我们通常把坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)(如图28.2-18 所示),坡度(坡比)也可写成i = h∶l的形式,在实际应用中常表示成1∶x的形式.
知4-讲
感悟新知
2. 坡度与坡角的关系:
=tanα ,即坡度是坡角的正切值,坡角越大,坡度也就越大.
感悟新知
知4-练
如图28.2-19,李明在大楼30 m 高(即PH=30 m)的窗口P 处进行观测,测得山坡上A 处的俯角为15°,山脚B 处的俯角为60° . 已知该山坡的坡度i 为1 ∶ ,点P,H,B,C,A 在同一个平面内,
点H,B,C 在同一条直线上,
且PH ⊥ HC.
例 5
感悟新知
知4-练
(1)山坡坡角的度数等于 ______°;
(2)求A,B 两点间的距离(结果精确到0.1 m,参考数据:
≈ 1.732).
解题秘方:将分散的条件集中到△ ABP 中求解.
30
∵山坡坡角为∠ ABC,
坡度i=1 ∶ ,
∴ tan ∠ ABC=
∴∠ ABC=30° .
感悟新知
知4-练
解:由题意,得∠ PBH=60°,
∠ APB=60° -15° =45° .
∵∠ ABC=30°,∴∠ ABP=90° .
∴∠ BAP=45°,∴ PB=AB.
在Rt △ PHB 中,
∴ AB=PB=20 ≈ 34.6m.
∴ A,B 两点间的距离约为34.6 m.
感悟新知
知4-练
5-1. [中考· 益阳]沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD, 高DH=12 米,斜坡CD 的坡度i=1 ∶ 1. 此处大堤的正上方有高压电线穿过,PD 表示高压线上的点与堤面AD 的最近距离(P,D,H 在同一直线上),在点C 处测得∠ DCP=26° .
感悟新知
知4-练
(1)求斜坡CD 的坡角α ;
感悟新知
知4-练
(2)电力部门要求此处高压线离堤面AD 的安全距离不低于18 米,请问此次改造是否符合电力部门的安全要求?(参考数据:sin 26°≈0.44,tan 26°≈ 0.49,sin 71 ° ≈ 0.95,tan71°≈ 2.90)
感悟新知
知4-练
课堂小结
应用举例
仰角和俯角问题
坡角和坡度问题
解直角三角形的应用类型
方向角问题
一般步骤
一般测量问题
