人教版九年级下册28.1锐角三角函数 课件(共59张PPT)
文档属性
| 名称 | 人教版九年级下册28.1锐角三角函数 课件(共59张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 11:42:46 | ||
图片预览







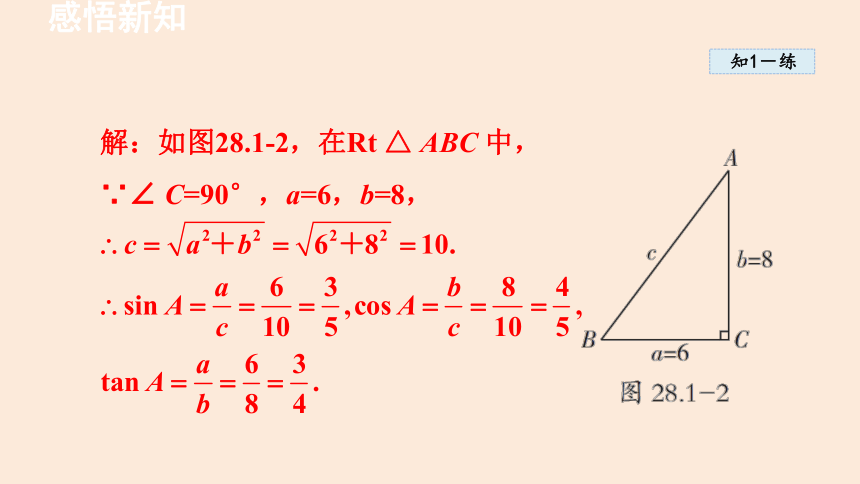


文档简介
(共59张PPT)
28.1 锐角三角函数
第28章 锐角三角函数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
锐角三角函数的定义
锐角三角函数之间的关系
特殊角的三角函数值
任一锐角的三角函数值
知识点
锐角三角函数的定义
知1-讲
感悟新知
1
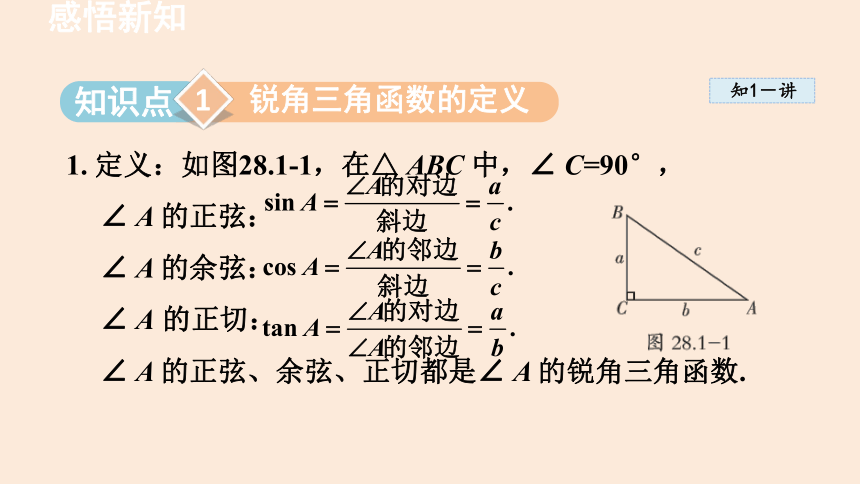
1. 定义:如图28.1-1,在△ ABC 中,∠ C=90°,
∠ A 的正弦:
∠ A 的余弦:
∠ A 的正切:
∠ A 的正弦、余弦、正切都是∠ A 的锐角三角函数.
知1-讲
感悟新知
2. 表示法:
(1)在sin A,cos A,tan A 中,三角函数的符号一定要小写,不能大写.
(2)当锐角是用一个大写英文字母或一个小写希腊字母表示时,它的三角函数习惯上省略角的符号,如sin A,
cos α ,tan B 等;当锐角是用三个大写英文字母或数字表示时,它的三角函数不能省略角的符号,如sin ∠ ABC,sin ∠ 1 等.
知1-讲
感悟新知
(3)“sin A”“cos A”“tan A”是整体符号,不能理解为“sin·A”“cos ·A”“tan·A”.
(4)sin2A 表示sin A·sin A=(sin A)2,不能写成sin A2;cos2A 表示cos A·cos A=(cos A)2,不能写成cos A2;tan2A 表示tan A·tan A=(tan A)2,不能写成tan A2.
知1-讲
感悟新知
特别提醒
1. 正弦、余弦、正切都是一个比值,是没有单位的数值,它们只与锐角的大小有关,而与三角形的边的长短无关.
2. 由于直角三角形的斜边大于直角边,且各边的长均为正实数,所以锐角三角函数值都是正实数, 且00.
知1-讲
感悟新知
3. 正弦、余弦、正切符号后面可以直接写锐角的度数,如sin28°,cos8°,tan18°等.
4. sin x,cos x 和tan x都是以x 为自变量的函数,一旦x 的度数确定,它们的值就唯一确定,即锐角三角函数值角度的变化而变化 .
感悟新知
知1-练
在Rt △ ABC 中,∠ C=90°,∠ A,∠ B,∠ C 的对边分别为a,b,c. 已知a=6,b=8,求出∠ A 的三角函数值.
例 1
解题秘方:紧扣“锐角三角函数的定义”求解.
感悟新知
知1-练
方法点拨:已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想, 首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求锐角的三角函数值.
感悟新知
知1-练
解:如图28.1-2,在Rt △ ABC 中,
∵∠ C=90°,a=6,b=8,
感悟新知
知1-练
1-1. 如图,在矩形纸片ABCD 中,AB=9,BC=12, 把△ BCD沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于点G,则sin ∠ ABG 的值为( )
D
感悟新知
知1-练
在△ ABC 中,∠ C=90°,sin A= ,则tan B=( )
解题秘方:当三角形出现边与边的比时,可引入参数,用这个参数表示出三角形的三边长,再用定义求解.
例2
B
感悟新知
知1-练
技巧点拨:在直角三角形中,给出某一锐角的三角函数值,求另一个锐角的三角函数值时,可以用设辅助元即引入“参数”的方法来解决,注意在最后计算时约去辅助元.
感悟新知
知1-练
解:由sin A= ,可设BC=4k(k>0),
则AB=5k,根据勾股定理,得AC=3k,
∴ tan B=
感悟新知
知1-练
2-1. 已知sinα = ,α 为锐角,求cosα 和tanα 的值.
感悟新知
知1-练
感悟新知
知1-练
如图28.1-3,在等腰三角形ABC 中,AB=AC,如果
2AB=3BC,求∠ B 的三个三角函数值.
例 3
解题秘方:紧扣“锐角三角函数的定义的前提是在直角三角形中”这一特征,用“构造直角三角形法”求解.
感悟新知
知1-练
解:过点A 作AD ⊥ BC 于点D,如图28.1-3,
∵ AB=AC,∴ BD=DC.
又∵ 2AB=3BC,∴
设AB=AC=3k(k>0),则BC=2k. ∴ BD=CD=k,
感悟新知
知1-练
3-1. 将一副三角尺(Rt△ ABC 与Rt△BDC)按如图所示的方式摆放在一起,连接AD, 试求∠ ADB 的正切值.
感悟新知
知1-练
感悟新知
知1-练
如图28.1-4, 在△ ABC 中, ∠ ACB=90 °,AC=BC=4,将△ ABC 折叠,使点A 落在BC 边上的点D 处,EF 是折痕,若AE=3,则sin ∠ BFD 的值为( )
例4
A
感悟新知
知1-练
解题秘方:紧扣“角相等则其三角函数值也相等”这一特征,用“等角转换法”将所要求的角的三角函数值转化为求直角三角形中与该角相等的角的三角函数值.
感悟新知
知1-练
解:∵在△ ABC 中,∠ ACB=90°,
AC=BC=4,∴∠ A = ∠ B.
由折叠得到DE=AE=3,∠ EDF = ∠ A,∴∠ EDF = ∠ B.
∵ ∠ CDF = ∠ CDE + ∠ EDF = ∠ B + ∠ BFD,
∴∠ CDE = ∠ BFD.
在Rt △ CDE 中,∵ CE=AC-AE=1,
∴ sin ∠ CDE= ,∴ sin ∠ BFD 的值为 .
感悟新知
知1-练
4-1. 如图,CD 是Rt △ ABC 斜边上的高,AC=4,BC=3,求cos ∠ BCD 的值.
感悟新知
知1-练
知识点
锐角三角函数之间的关系
知2-讲
感悟新知
2
1. 同一锐角的三角函数之间的关系:
(1)平方关系:sin2A+cos2A=1.
(2)商除关系: =tan A.
2. 互余两角的三角函数之间的关系:
sin A= cos(90°-∠ A).
cos A=sin(90 °-∠ A).
知2-讲
感悟新知
深度理解
1. 锐角三角函数之间的关系都可用定义推理得出.
2. 锐角三角函数定义速记口诀:
正弦等于对比斜,
余弦等于邻比斜,
正切等于对比邻,
函数特点要牢记.
感悟新知
知2-练
已知α 为锐角且sinα= ,求cosα,tanα 的值.
解题秘方:紧扣“同一锐角三角函数间的关系”求解.
解:∵ sin2α+cos2α=1,∴ cos2α=1-sin2α=1-
又α 为锐角,∴ 0 < cosα < 1,∴ cosα =
∴ tanα =
例 5
感悟新知
知2-练
5-1. 在Rt △ ABC 中,∠C=90°,sinA= ,求cosA,tanA 的值.
感悟新知
知2-练
计算:sin21°+sin22°+…+sin288°+sin289°.
解题秘方:紧扣sin α =cos(90°-α )将原式变形,再根据sin2α +cos2α =1 求解.
例6
解法提醒:灵活运用关系式sin2α +cos2α =1 与sinα =cos(90°-α )(0° <α <90°)是解答本题的关键. 当∠ A 为锐角时,关系式sin2A+cos2A=1,可变形为sin A= cos A=
知2-讲
感悟新知
解:原式=sin21°+sin22°+…+sin244°+sin245°+cos244°+…+cos22°+cos21°
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+sin245°
=44+ =44
感悟新知
知2-练
6-1. 在△ ABC 中,已知∠C=90°,sinA+sinB= ,求sin A-sin B的值.
感悟新知
知2-练
知识点
特殊角的三角函数值
知3-讲
感悟新知
3
1.30°,45°,60°角的三角函数值:
α 三角函数 30° 45° 60°
sin α
cos α
tan α 1
知3-讲
感悟新知
2. 30°,45°,60°角的三角函数值的记忆法:
巧记特殊角的三角函数值:
三十、四十五、六十度,三角函数要记住,
分母弦二切是三,分子要把根号添,
一二三来三二一,切值三、九、二十七,
正弦正切递增值,余弦递减恰相反.
知3-讲
感悟新知
特别提醒
1. 由左表可以计算特殊锐角的三角函数值,也可由特殊角的三角函数值求出相应的锐角.
2. 2sin60°表示sin60°的2倍,书写时省略2 与sin60°之间的乘号,且应将数字2放在前面,不要写成sin60°·2,以免误以为是sin120° .
3. 对于含有三角函数的计算题,应先把相应的三角函数值代入,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
感悟新知
知3-练
(1)已知α=45°,求2sin2α-2 sinα·tanα+tan2α;
(2)计算
例 7
解题秘方:用“代入法”求值.
感悟新知
知3-练
感悟新知
知3-练
感悟新知
知3-练
7-1. 求下列各式的值.
(1)sin30 °-2cos60°+tan45°.
(2)
(3)(1- )0-|1-sin30° |+
感悟新知
知3-练
感悟新知
知3-练
在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B
满足 =0,试判断△ ABC 的形状,并说明理由.
解题秘方:先根据特殊角的三角函数值求出两个内角的度数,再判断三角形的形状.
例8
感悟新知
知3-练
方法点拨:已知三角函数值求角度,关键要注意两点:一要说明角是锐角;二要注意三角函数值与锐角之间是一一对应的关系.
感悟新知
知3-练
解:△ ABC 是直角三角形,理由如下:
感悟新知
知3-练
又∵∠ A,∠ B 均为锐角,
∴∠ A=60°,∠ B=30°.
∴∠ A + ∠ B=60°+30°=90°.
∴△ ABC 是直角三角形.
感悟新知
知3-练
8-1. 在锐角三角形ABC中, 若|sinA- |+(1-tanB)2=0,则∠ C的度数是( )
A.45° B.60°
C.75° D.105°
C
感悟新知
知3-练
8-2. 在Rt △ ABC 中,∠ C=90°,AB=2 ,AC= , 则∠ B 的度数为_________.
60°
知识点
任一锐角的三角函数值
知4-讲
感悟新知
4
1. 利用计算器求锐角三角函数值的方法:(1)当锐角的大小以度为单位时,可先按 (或 、 )键,然后输入角度值(可以是整数,也可以是小数),最后按 键,就可以在显示屏上显示出结果;(2)当锐角的大小以度、分、秒为单位时,要借助 键计算,按键顺序是:
(或 、 )、度数、 、分数、 、秒数、 、 .
知4-讲
感悟新知
2. 已知锐角三角函数值求锐角的度数的方法:如果是特殊角的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数. 求角的度数要先按 键,将 键、 键、 键转化成它们的第二功能键;当三角函数值为分数时,可先化成小 数.
知4-讲
感悟新知
特别提醒
●不同计算器的按键顺序不同,大体分两种情形:先按三角函数键,再按数字键;或先输入数字,再按三角函数键.
●用科学计算器进行运算时,输入的数字符号的顺序与书写时的顺序不一定相同,比如sin213° 15′,输入时应为(sin 13° 15′ )2.
感悟新知
知4-练
用计算器求sin 16°,cos 42°,tan 85°,sin 72°38′25″的值.
解题秘方:按计算器的使用说明求值.
例 9
感悟新知
知4-练
解:如下表:
按键顺序 显示结果
sin 16° 0.275 637 355
cos 42° 0.743 144 825
tan 85° 11. 430 052 3
sin72°38′25″ 0.954 450 312
感悟新知
知4-练
9-1. 用计算器求下列各式的值(结果精确到0.000 1).
(1)sin23°5′+cos66° 55′ .
(2)cos14°28′-tan42° 57′ .
(3)sin27.8°-cos65°37′+tan49°56′.
感悟新知
知4-练
解:(1)原式=sin23°5′+sin23°5′=2sin23°5′≈
2×0.392 07≈0.784 1.
(2)原式≈0.968 29-0.930 88≈0.037 4.
(3)原式≈0.135 722-0.412 84+1.188 94≈0.018 42-0.412 84+1.188 94≈0.794 5.
感悟新知
知4-练
已知下列锐角三角函数值,用计算器求其相应的锐角
的度数.
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″).
解题秘方:按计算器的使用说明依次按键.
例10
感悟新知
知4-练
解法提醒:计算器直接计算出的角度的单位是度,而不是度、分、秒,因此, 若要得到用度、分、秒表示的角度,可以借助 和 键.
感悟新知
知4-练
解:(1)依次按键: ,
显示结果为31.117 845 56,
即∠ A ≈ 31.12°
(2)依次按键: ,
显示结果为47°31′21.18″,
即∠ A ≈ 47°31′21″
感悟新知
知4-练
10-1. 为了方便行人推车过某天桥,市政府在10m 高的天桥一侧修建了一条40 m 长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角∠ A 的度数,具体按键顺序是( )
A.
B.
C.
D.
A
课堂小结
锐角三角函数
特殊角的三角函数值
锐角的三角函数值
锐角
三角
函数
计算
锐角的度数
定义
正弦
余弦
正切
28.1 锐角三角函数
第28章 锐角三角函数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
锐角三角函数的定义
锐角三角函数之间的关系
特殊角的三角函数值
任一锐角的三角函数值
知识点
锐角三角函数的定义
知1-讲
感悟新知
1
1. 定义:如图28.1-1,在△ ABC 中,∠ C=90°,
∠ A 的正弦:
∠ A 的余弦:
∠ A 的正切:
∠ A 的正弦、余弦、正切都是∠ A 的锐角三角函数.
知1-讲
感悟新知
2. 表示法:
(1)在sin A,cos A,tan A 中,三角函数的符号一定要小写,不能大写.
(2)当锐角是用一个大写英文字母或一个小写希腊字母表示时,它的三角函数习惯上省略角的符号,如sin A,
cos α ,tan B 等;当锐角是用三个大写英文字母或数字表示时,它的三角函数不能省略角的符号,如sin ∠ ABC,sin ∠ 1 等.
知1-讲
感悟新知
(3)“sin A”“cos A”“tan A”是整体符号,不能理解为“sin·A”“cos ·A”“tan·A”.
(4)sin2A 表示sin A·sin A=(sin A)2,不能写成sin A2;cos2A 表示cos A·cos A=(cos A)2,不能写成cos A2;tan2A 表示tan A·tan A=(tan A)2,不能写成tan A2.
知1-讲
感悟新知
特别提醒
1. 正弦、余弦、正切都是一个比值,是没有单位的数值,它们只与锐角的大小有关,而与三角形的边的长短无关.
2. 由于直角三角形的斜边大于直角边,且各边的长均为正实数,所以锐角三角函数值都是正实数, 且0
知1-讲
感悟新知
3. 正弦、余弦、正切符号后面可以直接写锐角的度数,如sin28°,cos8°,tan18°等.
4. sin x,cos x 和tan x都是以x 为自变量的函数,一旦x 的度数确定,它们的值就唯一确定,即锐角三角函数值角度的变化而变化 .
感悟新知
知1-练
在Rt △ ABC 中,∠ C=90°,∠ A,∠ B,∠ C 的对边分别为a,b,c. 已知a=6,b=8,求出∠ A 的三角函数值.
例 1
解题秘方:紧扣“锐角三角函数的定义”求解.
感悟新知
知1-练
方法点拨:已知直角三角形的任意两边长求某个锐角的三角函数值时,运用数形结合思想, 首先画出符合题意的直角三角形,然后根据勾股定理求出未知边长,最后结合锐角三角函数的定义求锐角的三角函数值.
感悟新知
知1-练
解:如图28.1-2,在Rt △ ABC 中,
∵∠ C=90°,a=6,b=8,
感悟新知
知1-练
1-1. 如图,在矩形纸片ABCD 中,AB=9,BC=12, 把△ BCD沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于点G,则sin ∠ ABG 的值为( )
D
感悟新知
知1-练
在△ ABC 中,∠ C=90°,sin A= ,则tan B=( )
解题秘方:当三角形出现边与边的比时,可引入参数,用这个参数表示出三角形的三边长,再用定义求解.
例2
B
感悟新知
知1-练
技巧点拨:在直角三角形中,给出某一锐角的三角函数值,求另一个锐角的三角函数值时,可以用设辅助元即引入“参数”的方法来解决,注意在最后计算时约去辅助元.
感悟新知
知1-练
解:由sin A= ,可设BC=4k(k>0),
则AB=5k,根据勾股定理,得AC=3k,
∴ tan B=
感悟新知
知1-练
2-1. 已知sinα = ,α 为锐角,求cosα 和tanα 的值.
感悟新知
知1-练
感悟新知
知1-练
如图28.1-3,在等腰三角形ABC 中,AB=AC,如果
2AB=3BC,求∠ B 的三个三角函数值.
例 3
解题秘方:紧扣“锐角三角函数的定义的前提是在直角三角形中”这一特征,用“构造直角三角形法”求解.
感悟新知
知1-练
解:过点A 作AD ⊥ BC 于点D,如图28.1-3,
∵ AB=AC,∴ BD=DC.
又∵ 2AB=3BC,∴
设AB=AC=3k(k>0),则BC=2k. ∴ BD=CD=k,
感悟新知
知1-练
3-1. 将一副三角尺(Rt△ ABC 与Rt△BDC)按如图所示的方式摆放在一起,连接AD, 试求∠ ADB 的正切值.
感悟新知
知1-练
感悟新知
知1-练
如图28.1-4, 在△ ABC 中, ∠ ACB=90 °,AC=BC=4,将△ ABC 折叠,使点A 落在BC 边上的点D 处,EF 是折痕,若AE=3,则sin ∠ BFD 的值为( )
例4
A
感悟新知
知1-练
解题秘方:紧扣“角相等则其三角函数值也相等”这一特征,用“等角转换法”将所要求的角的三角函数值转化为求直角三角形中与该角相等的角的三角函数值.
感悟新知
知1-练
解:∵在△ ABC 中,∠ ACB=90°,
AC=BC=4,∴∠ A = ∠ B.
由折叠得到DE=AE=3,∠ EDF = ∠ A,∴∠ EDF = ∠ B.
∵ ∠ CDF = ∠ CDE + ∠ EDF = ∠ B + ∠ BFD,
∴∠ CDE = ∠ BFD.
在Rt △ CDE 中,∵ CE=AC-AE=1,
∴ sin ∠ CDE= ,∴ sin ∠ BFD 的值为 .
感悟新知
知1-练
4-1. 如图,CD 是Rt △ ABC 斜边上的高,AC=4,BC=3,求cos ∠ BCD 的值.
感悟新知
知1-练
知识点
锐角三角函数之间的关系
知2-讲
感悟新知
2
1. 同一锐角的三角函数之间的关系:
(1)平方关系:sin2A+cos2A=1.
(2)商除关系: =tan A.
2. 互余两角的三角函数之间的关系:
sin A= cos(90°-∠ A).
cos A=sin(90 °-∠ A).
知2-讲
感悟新知
深度理解
1. 锐角三角函数之间的关系都可用定义推理得出.
2. 锐角三角函数定义速记口诀:
正弦等于对比斜,
余弦等于邻比斜,
正切等于对比邻,
函数特点要牢记.
感悟新知
知2-练
已知α 为锐角且sinα= ,求cosα,tanα 的值.
解题秘方:紧扣“同一锐角三角函数间的关系”求解.
解:∵ sin2α+cos2α=1,∴ cos2α=1-sin2α=1-
又α 为锐角,∴ 0 < cosα < 1,∴ cosα =
∴ tanα =
例 5
感悟新知
知2-练
5-1. 在Rt △ ABC 中,∠C=90°,sinA= ,求cosA,tanA 的值.
感悟新知
知2-练
计算:sin21°+sin22°+…+sin288°+sin289°.
解题秘方:紧扣sin α =cos(90°-α )将原式变形,再根据sin2α +cos2α =1 求解.
例6
解法提醒:灵活运用关系式sin2α +cos2α =1 与sinα =cos(90°-α )(0° <α <90°)是解答本题的关键. 当∠ A 为锐角时,关系式sin2A+cos2A=1,可变形为sin A= cos A=
知2-讲
感悟新知
解:原式=sin21°+sin22°+…+sin244°+sin245°+cos244°+…+cos22°+cos21°
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+sin245°
=44+ =44
感悟新知
知2-练
6-1. 在△ ABC 中,已知∠C=90°,sinA+sinB= ,求sin A-sin B的值.
感悟新知
知2-练
知识点
特殊角的三角函数值
知3-讲
感悟新知
3
1.30°,45°,60°角的三角函数值:
α 三角函数 30° 45° 60°
sin α
cos α
tan α 1
知3-讲
感悟新知
2. 30°,45°,60°角的三角函数值的记忆法:
巧记特殊角的三角函数值:
三十、四十五、六十度,三角函数要记住,
分母弦二切是三,分子要把根号添,
一二三来三二一,切值三、九、二十七,
正弦正切递增值,余弦递减恰相反.
知3-讲
感悟新知
特别提醒
1. 由左表可以计算特殊锐角的三角函数值,也可由特殊角的三角函数值求出相应的锐角.
2. 2sin60°表示sin60°的2倍,书写时省略2 与sin60°之间的乘号,且应将数字2放在前面,不要写成sin60°·2,以免误以为是sin120° .
3. 对于含有三角函数的计算题,应先把相应的三角函数值代入,将运算转化为实数的混合运算,然后根据实数的运算法则计算.
感悟新知
知3-练
(1)已知α=45°,求2sin2α-2 sinα·tanα+tan2α;
(2)计算
例 7
解题秘方:用“代入法”求值.
感悟新知
知3-练
感悟新知
知3-练
感悟新知
知3-练
7-1. 求下列各式的值.
(1)sin30 °-2cos60°+tan45°.
(2)
(3)(1- )0-|1-sin30° |+
感悟新知
知3-练
感悟新知
知3-练
在△ ABC 中,∠ A,∠ B 均为锐角,且∠ A,∠ B
满足 =0,试判断△ ABC 的形状,并说明理由.
解题秘方:先根据特殊角的三角函数值求出两个内角的度数,再判断三角形的形状.
例8
感悟新知
知3-练
方法点拨:已知三角函数值求角度,关键要注意两点:一要说明角是锐角;二要注意三角函数值与锐角之间是一一对应的关系.
感悟新知
知3-练
解:△ ABC 是直角三角形,理由如下:
感悟新知
知3-练
又∵∠ A,∠ B 均为锐角,
∴∠ A=60°,∠ B=30°.
∴∠ A + ∠ B=60°+30°=90°.
∴△ ABC 是直角三角形.
感悟新知
知3-练
8-1. 在锐角三角形ABC中, 若|sinA- |+(1-tanB)2=0,则∠ C的度数是( )
A.45° B.60°
C.75° D.105°
C
感悟新知
知3-练
8-2. 在Rt △ ABC 中,∠ C=90°,AB=2 ,AC= , 则∠ B 的度数为_________.
60°
知识点
任一锐角的三角函数值
知4-讲
感悟新知
4
1. 利用计算器求锐角三角函数值的方法:(1)当锐角的大小以度为单位时,可先按 (或 、 )键,然后输入角度值(可以是整数,也可以是小数),最后按 键,就可以在显示屏上显示出结果;(2)当锐角的大小以度、分、秒为单位时,要借助 键计算,按键顺序是:
(或 、 )、度数、 、分数、 、秒数、 、 .
知4-讲
感悟新知
2. 已知锐角三角函数值求锐角的度数的方法:如果是特殊角的三角函数值,可直接写出其相应的角的度数;若不是特殊角的三角函数值,应利用计算器求角的度数. 求角的度数要先按 键,将 键、 键、 键转化成它们的第二功能键;当三角函数值为分数时,可先化成小 数.
知4-讲
感悟新知
特别提醒
●不同计算器的按键顺序不同,大体分两种情形:先按三角函数键,再按数字键;或先输入数字,再按三角函数键.
●用科学计算器进行运算时,输入的数字符号的顺序与书写时的顺序不一定相同,比如sin213° 15′,输入时应为(sin 13° 15′ )2.
感悟新知
知4-练
用计算器求sin 16°,cos 42°,tan 85°,sin 72°38′25″的值.
解题秘方:按计算器的使用说明求值.
例 9
感悟新知
知4-练
解:如下表:
按键顺序 显示结果
sin 16° 0.275 637 355
cos 42° 0.743 144 825
tan 85° 11. 430 052 3
sin72°38′25″ 0.954 450 312
感悟新知
知4-练
9-1. 用计算器求下列各式的值(结果精确到0.000 1).
(1)sin23°5′+cos66° 55′ .
(2)cos14°28′-tan42° 57′ .
(3)sin27.8°-cos65°37′+tan49°56′.
感悟新知
知4-练
解:(1)原式=sin23°5′+sin23°5′=2sin23°5′≈
2×0.392 07≈0.784 1.
(2)原式≈0.968 29-0.930 88≈0.037 4.
(3)原式≈0.135 722-0.412 84+1.188 94≈0.018 42-0.412 84+1.188 94≈0.794 5.
感悟新知
知4-练
已知下列锐角三角函数值,用计算器求其相应的锐角
的度数.
(1)sin A=0.516 8(结果精确到0.01°);
(2)cos A=0.675 3(结果精确到1″).
解题秘方:按计算器的使用说明依次按键.
例10
感悟新知
知4-练
解法提醒:计算器直接计算出的角度的单位是度,而不是度、分、秒,因此, 若要得到用度、分、秒表示的角度,可以借助 和 键.
感悟新知
知4-练
解:(1)依次按键: ,
显示结果为31.117 845 56,
即∠ A ≈ 31.12°
(2)依次按键: ,
显示结果为47°31′21.18″,
即∠ A ≈ 47°31′21″
感悟新知
知4-练
10-1. 为了方便行人推车过某天桥,市政府在10m 高的天桥一侧修建了一条40 m 长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角∠ A 的度数,具体按键顺序是( )
A.
B.
C.
D.
A
课堂小结
锐角三角函数
特殊角的三角函数值
锐角的三角函数值
锐角
三角
函数
计算
锐角的度数
定义
正弦
余弦
正切
