人教版数学九下29.2 三视图29.3 课题学习 制作立体模型 课件(共34张PPT)
文档属性
| 名称 | 人教版数学九下29.2 三视图29.3 课题学习 制作立体模型 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:43:28 | ||
图片预览








文档简介
(共34张PPT)
29.2 三视图
29.3 课题学习 制作立体模型
第29章 投影与视图
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
视图及相关概念
由几何体画三视图
由三视图确定几何体
由三视图制作立体模型
知识点
视图及相关概念
知1-讲
感悟新知
1
1. 视图: 用正投影的方法绘制的物体在投影面上的图形,称为物体的视图.
2. 三视图: 我们把从正面得到的视图叫做主视图,从左面得到的视图叫做左视图,从上面得到的视图叫做俯视图.
知1-讲
感悟新知
3. 三视图与正投影的关系: 某些物体的三视图实际上是该物体在一定条件下所形成的正投影,某些物体的主视图、左视图、俯视图可以看成一束平行光线分别从物体的正面、左面、上面照射,在垂直于这一光线方向的平面上所形成的正投影.
知1-讲
感悟新知
速记口诀
视图来源正投影,
三个方向实物成,
从前向后主视图,
从上向下俯视图,
从左向右左视图,
统称物体三视图.
感悟新知
知1-练
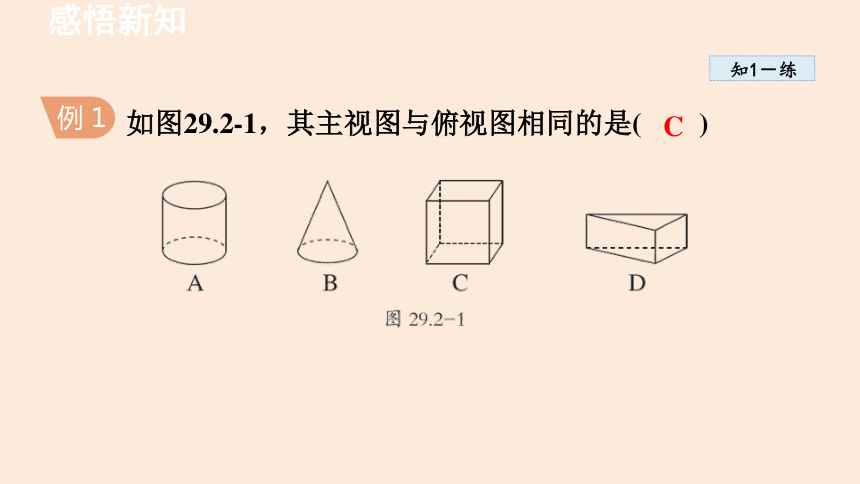
如图29.2-1,其主视图与俯视图相同的是( )
例 1
C
感悟新知
知1-练
解:A 中主视图是矩形,俯视图是圆,故不符合题意;B中主视图是三角形,俯视图是带圆心的圆,故不符合题意;C中主视图和俯视图都是正方形,故符合题意;D 中主视图的外轮廓线是矩形,俯视图是三角形,故不符合题意.
解题秘方:紧扣“三视图的定义”,想象几何体正面、上面的正投影的几何形状进行解答.
感悟新知
知1-练
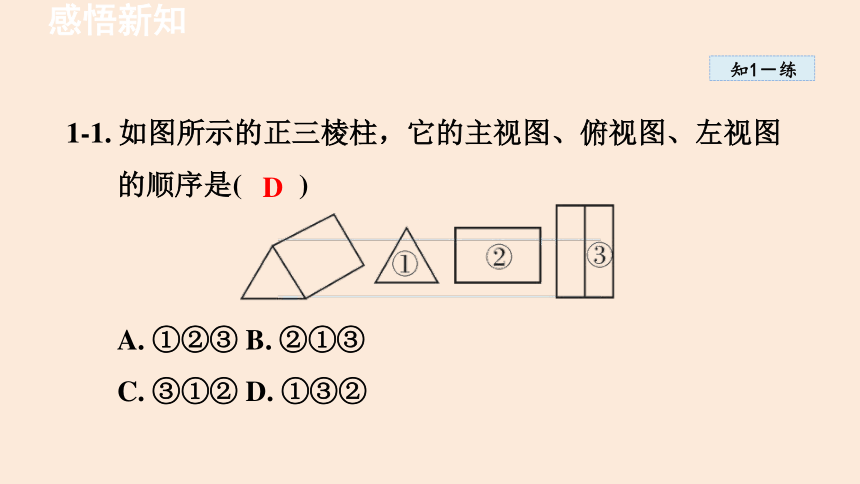
1-1. 如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是( )
A. ①②③ B. ②①③
C. ③①② D. ①③②
D
知识点
由几何体画三视图
知2-讲
感悟新知
2
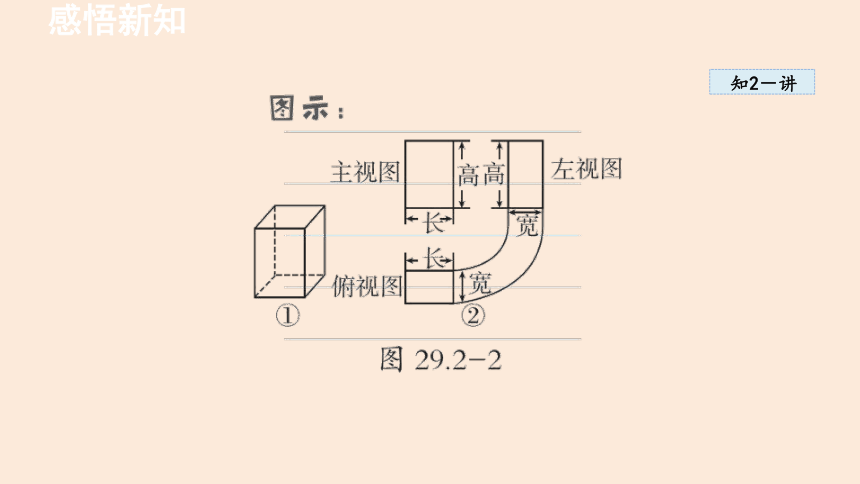
1. 三种视图之间的关系:
(1)位置关系:主视图在左上边,主视图的正下方是俯视图,左视图在主视图的右边,主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
(2)大小关系:三视图之间的大小是相互联系的,主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
知2-讲
感悟新知
速记口诀
视图位置要摆明,
画图规则要记清.
主俯视图长对正,
左俯视图宽相等.
主左视图高平齐,
实线虚线应分清.
知2-讲
感悟新知
2. 三视图的画法:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,并且主视图与俯视图长对正;
(3)在主视图的正右方画出左视图,与主视图高平齐,与俯视图宽相等.
知2-讲
感悟新知
感悟新知
知2-练
画出图29.2-3 中几何体的三视图.
例2
解题秘方:紧扣“三视图的画法”画出几何体的三视图.
知2-讲
感悟新知
画法提醒:画几何体的三视图时,要仔细观察几何体,从要看的方向将几何体压缩到面上,使几何体在这一方向上没有厚度,同时要特别注意三视图之间应遵循:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
知2-讲
感悟新知
解:该几何体由一个长方体和一个三棱柱组合而成,依据三视图的定义,可得该几何体的三视图如图29.2-4.
感悟新知
知2-练
2-1. [中考 台州] 用三个相同的正方体搭成如图所示的几何体,则该几何体的主视图是( )
D
感悟新知
知2-练
一种机器上有一个零件叫燕尾槽(如图29.2-5),请
画出它的三视图.
解题秘方:紧扣三视图的画法步骤,关键是分清实线和虚线.
例 3
知2-讲
感悟新知
解:这个燕尾槽的三视图如图29.2-6.
感悟新知
知2-练
3-1. 如图,圆柱中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
D
知识点
由三视图确定几何体
知3-讲
感悟新知
3
1. 由三视图描述几何体的方法:由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面,然后综合起来考虑整体形状.
知3-讲
感悟新知
2. 常见几何体的三视图:
知3-讲
感悟新知
几何体、三视图和展开图之间的关系:
1. 几何体的三视图和展开图是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2. 一个几何体的三视图是唯一的,但从三视图反过来考虑几何体时,它有多种可能性.
感悟新知
知3-练
某几何体的三视图如图29.2-7,则该几何体是( )
A. 三棱柱
B. 长方体
C. 圆柱
D. 圆锥
例4
D
感悟新知
知3-练
解题秘方:紧扣“几何体的三视图”进行识别.
解:用排除法:由俯视图的外轮廓线是圆,排除A 和B;由主视图是三角形,排除C.
感悟新知
知3-练
4-1. 一个几何体的三视图如图所示,则这个立体图形是( )
D
知识点
由三视图制作立体模型
知4-讲
感悟新知
4
1. 由三视图制作立体模型的一般方法:
观察三视图,理解各视图表达的含义,想象各视图表示的物体的形状,将平面图形制作成立体模型.
2. 制作工具:
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
知4-讲
感悟新知
特别说明
根据三视图制作立体模型时,一般以硬纸板作为主要材料.
感悟新知
知4-练
如图29.2-8 所示(单位:cm)是某校升旗台的三视图.
(1)用萝卜做出升旗台的立体模型;
(2)计算出升旗台的体积.
例 5
解题秘方:根据三视图确定物体的形状,并结合三视图中的数据确定物体的数据进行模型的制作及计算.
感悟新知
知4-练
解:(1)立体模型如图29.2-9 所示.
感悟新知
知4-练
(2)升旗台的体积为
150×(40×20+40×40+40×60)=150×4 800=
720 000(cm3).
感悟新知
知4-练
5-1. 如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的最
确切的名称是_________.
直三棱柱
感悟新知
知4-练
(2)如图②是根据a,h的取值画出的该几何体的主视图和俯视图[ 图中的粗实线表示正方形(中间一条虚线)和三角形],请在网格中画出该几何体的左视图.
感悟新知
知4-练
解:左视图如图所示.
课堂小结
三视图
课题学习 制作立体模型
画法
应用
三视图
主视图
左视图
俯视图
29.2 三视图
29.3 课题学习 制作立体模型
第29章 投影与视图
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
视图及相关概念
由几何体画三视图
由三视图确定几何体
由三视图制作立体模型
知识点
视图及相关概念
知1-讲
感悟新知
1
1. 视图: 用正投影的方法绘制的物体在投影面上的图形,称为物体的视图.
2. 三视图: 我们把从正面得到的视图叫做主视图,从左面得到的视图叫做左视图,从上面得到的视图叫做俯视图.
知1-讲
感悟新知
3. 三视图与正投影的关系: 某些物体的三视图实际上是该物体在一定条件下所形成的正投影,某些物体的主视图、左视图、俯视图可以看成一束平行光线分别从物体的正面、左面、上面照射,在垂直于这一光线方向的平面上所形成的正投影.
知1-讲
感悟新知
速记口诀
视图来源正投影,
三个方向实物成,
从前向后主视图,
从上向下俯视图,
从左向右左视图,
统称物体三视图.
感悟新知
知1-练
如图29.2-1,其主视图与俯视图相同的是( )
例 1
C
感悟新知
知1-练
解:A 中主视图是矩形,俯视图是圆,故不符合题意;B中主视图是三角形,俯视图是带圆心的圆,故不符合题意;C中主视图和俯视图都是正方形,故符合题意;D 中主视图的外轮廓线是矩形,俯视图是三角形,故不符合题意.
解题秘方:紧扣“三视图的定义”,想象几何体正面、上面的正投影的几何形状进行解答.
感悟新知
知1-练
1-1. 如图所示的正三棱柱,它的主视图、俯视图、左视图的顺序是( )
A. ①②③ B. ②①③
C. ③①② D. ①③②
D
知识点
由几何体画三视图
知2-讲
感悟新知
2
1. 三种视图之间的关系:
(1)位置关系:主视图在左上边,主视图的正下方是俯视图,左视图在主视图的右边,主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
(2)大小关系:三视图之间的大小是相互联系的,主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
知2-讲
感悟新知
速记口诀
视图位置要摆明,
画图规则要记清.
主俯视图长对正,
左俯视图宽相等.
主左视图高平齐,
实线虚线应分清.
知2-讲
感悟新知
2. 三视图的画法:
(1)确定主视图的位置,画出主视图;
(2)在主视图的正下方画出俯视图,并且主视图与俯视图长对正;
(3)在主视图的正右方画出左视图,与主视图高平齐,与俯视图宽相等.
知2-讲
感悟新知
感悟新知
知2-练
画出图29.2-3 中几何体的三视图.
例2
解题秘方:紧扣“三视图的画法”画出几何体的三视图.
知2-讲
感悟新知
画法提醒:画几何体的三视图时,要仔细观察几何体,从要看的方向将几何体压缩到面上,使几何体在这一方向上没有厚度,同时要特别注意三视图之间应遵循:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
知2-讲
感悟新知
解:该几何体由一个长方体和一个三棱柱组合而成,依据三视图的定义,可得该几何体的三视图如图29.2-4.
感悟新知
知2-练
2-1. [中考 台州] 用三个相同的正方体搭成如图所示的几何体,则该几何体的主视图是( )
D
感悟新知
知2-练
一种机器上有一个零件叫燕尾槽(如图29.2-5),请
画出它的三视图.
解题秘方:紧扣三视图的画法步骤,关键是分清实线和虚线.
例 3
知2-讲
感悟新知
解:这个燕尾槽的三视图如图29.2-6.
感悟新知
知2-练
3-1. 如图,圆柱中挖去一个小圆柱,那么这个几何体的主视图和俯视图分别为( )
D
知识点
由三视图确定几何体
知3-讲
感悟新知
3
1. 由三视图描述几何体的方法:由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的正面、上面和左面,然后综合起来考虑整体形状.
知3-讲
感悟新知
2. 常见几何体的三视图:
知3-讲
感悟新知
几何体、三视图和展开图之间的关系:
1. 几何体的三视图和展开图是平面图形,几何体、三视图和展开图中,三者知其一,就能确定另外两种图形, 即三者之间可以互相转化.
2. 一个几何体的三视图是唯一的,但从三视图反过来考虑几何体时,它有多种可能性.
感悟新知
知3-练
某几何体的三视图如图29.2-7,则该几何体是( )
A. 三棱柱
B. 长方体
C. 圆柱
D. 圆锥
例4
D
感悟新知
知3-练
解题秘方:紧扣“几何体的三视图”进行识别.
解:用排除法:由俯视图的外轮廓线是圆,排除A 和B;由主视图是三角形,排除C.
感悟新知
知3-练
4-1. 一个几何体的三视图如图所示,则这个立体图形是( )
D
知识点
由三视图制作立体模型
知4-讲
感悟新知
4
1. 由三视图制作立体模型的一般方法:
观察三视图,理解各视图表达的含义,想象各视图表示的物体的形状,将平面图形制作成立体模型.
2. 制作工具:
刻度尺、剪刀、小刀、胶水、硬纸板、马铃薯(或萝卜)等.
知4-讲
感悟新知
特别说明
根据三视图制作立体模型时,一般以硬纸板作为主要材料.
感悟新知
知4-练
如图29.2-8 所示(单位:cm)是某校升旗台的三视图.
(1)用萝卜做出升旗台的立体模型;
(2)计算出升旗台的体积.
例 5
解题秘方:根据三视图确定物体的形状,并结合三视图中的数据确定物体的数据进行模型的制作及计算.
感悟新知
知4-练
解:(1)立体模型如图29.2-9 所示.
感悟新知
知4-练
(2)升旗台的体积为
150×(40×20+40×40+40×60)=150×4 800=
720 000(cm3).
感悟新知
知4-练
5-1. 如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)这个几何体模型的最
确切的名称是_________.
直三棱柱
感悟新知
知4-练
(2)如图②是根据a,h的取值画出的该几何体的主视图和俯视图[ 图中的粗实线表示正方形(中间一条虚线)和三角形],请在网格中画出该几何体的左视图.
感悟新知
知4-练
解:左视图如图所示.
课堂小结
三视图
课题学习 制作立体模型
画法
应用
三视图
主视图
左视图
俯视图
