人教版数学九下26.2 实际问题与反比例函数 课件(共46张PPT)
文档属性
| 名称 | 人教版数学九下26.2 实际问题与反比例函数 课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:44:09 | ||
图片预览










文档简介
(共46张PPT)
26.2 实际问题与反比例函数
第26章 反比例函数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
建立反比例函数模型解实际问题
知识点
建立反比例函数模型解实际问题
知1-讲
感悟新知
1
1. 在生活与生产中,如果某些问题的两个量成反比例关系,那么可以根据这种关系建立反比例函数模型,再利用反比例函数的有关知识解决实际问题.
特别提醒
利用反比例函数解决实际问题时应注意:
1.要理清题目中的常量与变量及其基本数量关系;
2.结合问题的实际意义,确定自变量的取值范围;
3.要熟练掌握反比例函数的意义、图象和性质.
知1-讲
感悟新知
运用反比例函数解决实际问题时常用的两种思路:
(1)通过问题提供的信息,明确变量之间的函数关系,设出相应的函数解析式,再根据题目条件确定函数解析式中的待定系数的值;
(2)已知反比例函数模型的解析式,运用反比例函数的图象及性质解决问题.
知1-讲
感悟新知
2. 用反比例函数解决实际问题的一般步骤
(1)审(2)设(3)列(4)写(5)解
感悟新知
知1-练
某地区上一年度每度电价格为0.8 元,年用电量为1亿度,本年度计划将电价调到0.55元~0.75元(不包括端点值).经测算,若电价调至x 元,则本年度新增用电量y(亿度)与(x-0.4)(元)成反比例,且当x=0.65 时,y=0.8.
例 1
感悟新知
知1-练
解题秘方:紧扣反比例关系用待定系数法设函数解析式求解.
(1)求y 与x 之间的函数解析式.
(2)若每度电的成本价为0.3 元,当电价调至0.72 元时,本年度电力部门的收益是多少元?
感悟新知
知1-练
解:(1)设y 与x 之间的函数解析式为y= (k ≠ 0).
∵当x=0.65 时,y=0.8,
∴ k=(x-0.4)y=(0.65-0.4)×0.8=0.2.
∴ y= ,
即y= (0.55 < x < 0.75).
感悟新知
知1-练
解:(2)当电价调至0.72 元时,新增用电量为
= 0.625(亿度),
则本年度用电量为1+0.625=1.625(亿度),
1.625 亿度=1.625×108 度.
∴(0.72-0.3)×1.625×108=6.825×107(元).
∴ 当电价调至0.72 元时, 本年度电力部门的收益是
6.825×107 元.
感悟新知
知1-练
1-1. 某户家庭用购电卡购买了2 000 度电, 若此户家庭平均每天的用电量为x(单位:度),这2 000 度电能够使用的天数为y(单位:天),则y 与x 的函数解析式为y= ____________(不要求写出自变量的取值范围).
感悟新知
知1-练
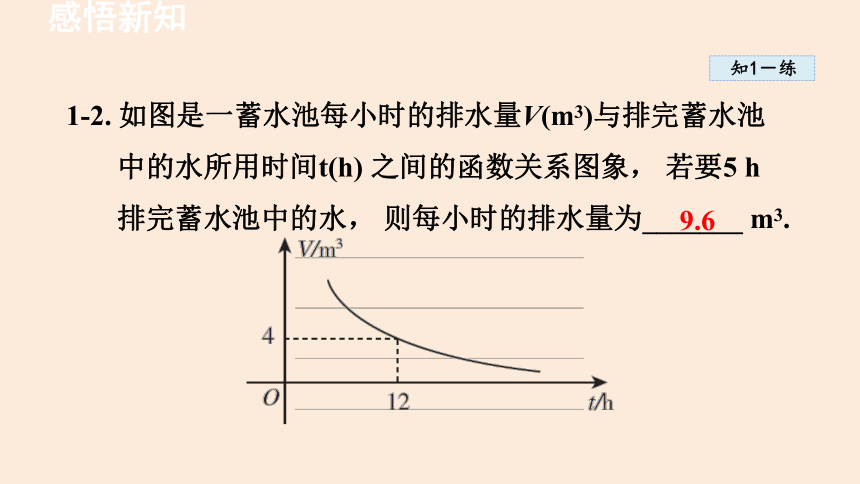
1-2. 如图是一蓄水池每小时的排水量V(m3)与排完蓄水池中的水所用时间t(h) 之间的函数关系图象, 若要5 h 排完蓄水池中的水, 则每小时的排水量为_______ m3.
9.6
感悟新知
知1-练
某机床加工一批机器零件,如果每小时加工30 个,
那么12 小时可以完成.
(1)设每小时加工x 个零件,所需时间为y 小时,写出y关于x 的函数解析式;
(2)若要在一个工作日(8 小时)内完成,每小时要比原来多加工几个零件?
例2
感悟新知
知1-练
解题秘方:紧扣工程问题中“工作总量、工作时间与工作效率”间的关系列式,变形即可求出函数解析式.
感悟新知
知1-练
解:(1)由题意得xy=30×12=360,
所以y 关于x 的函数解析式为y= (x > 0 且x 为整数).
(2)将y=8 代入y= 中,得8= , 解得x=45.
所以每小时要加工45 个. 45-30=15(个),
所以每小时要比原来多加工15 个零件.
感悟新知
知1-练
2-1. 某工厂生产化肥的总任务一定,平均每天的化肥产量y(吨)与完成总任务所需要的时间x(天)成反比例关系,如果平均每天生产化肥125 吨,那么完成总任务需要7 天.
感悟新知
知1-练
(1)求y 关于x 的函数解析式,并指出比例系数.
感悟新知
知1-练
(2)若要5 天完成总任务,则平均每天的化肥产量应达到多少?
感悟新知
知1-练
[中考·杭州] 方方驾驶小汽车匀速地从A 地行驶到B
地,行驶里程为480 km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120 km/h.
例 3
感悟新知
知1-练
解题秘方:紧扣行程问题中路程一定时,速度与时间之间的关系,利用反比例函数的性质解决问题.
(1)求v 关于t 的函数解析式.
(2)方方上午8 点驾驶小汽车从A 地出发.
①方方需在当天12 点48 分至14 点(含12 点48 分和14 点)间到达B 地,求小汽车行驶速度v 的范围.
②方方能否在当天11 点30 分前到达B 地 说明理由.
感悟新知
知1-练
解:(1)∵ vt=480,且v ≤ 120,
∴ v 关于t 的函数解析式为v= (t ≥ 4).
感悟新知
知1-练
(2)① 8 点至12 点48 分的时间长为 h,8 点至14 点
的时间长为6 h,∴ ≤ t ≤ 6.
将t=6 代入v= 中,得v=80;将t= 代入v= 中,
得v=100. ∴小汽车行驶速度v 的范围为80 ≤ v ≤ 100.
感悟新知
知1-练
②方方不能在当天11 点30 分前到达B 地. 理由如下:
8 点至11 点30 分的时间长为 h,将t= 代入v= ,
得v= >120,超速.
故方方不能在当天11 点30 分前到达B 地.
感悟新知
知1-练
3-1. 小芳为响应“ 绿色出行, 低碳生活”,每天从家骑自行车去学校, 所需时间v(min)与骑车速度x(m/min)之间的反比例函数关系如图.
感悟新知
知1-练
(1)写出y 关于x 的函数解析式.
感悟新知
知1-练
(2)学校要求学生每天最晚7 时20 分到校,为了安全起见, 小芳的骑车速度最快不超过300 m/min,则她每天最晚什么时候出发?
解:当x=300时,y=8. 20-8=12(min).
∴ 她每天最晚7时12分出发.
感悟新知
知1-练
某闭合电路中,其电压恒定,电流I(A)与电阻R(Ω)成反比例函数关系,其图象如图26.2-1,根据图象回答下列问题.
例4
感悟新知
知1-练
(1)写出电流I 与电阻R 之间的函数解析式.
(2)如果一个用电器的电阻为5 Ω,其允许通过的最大电流是1 A,那么这个用电器接在这个闭合电路中,会不会被烧毁?请说明理由.
(3)若允许通过的电流不超过4 A,那么电阻的取值应该控制在什么范围?
感悟新知
知1-练
解题秘方:紧扣“电压恒定,电流与电阻成反比例函数关系”,用待定系数法求反比例函数解析式,再结合函数解析式求解其他问题.
感悟新知
知1-练
解:(1)设I= (k ≠ 0),由图象过点(3,2),得2= , 解得k=6.
所以电流I 与电阻R 之间的函数解析式为I= .
感悟新知
知1-练
(2)会被烧毁. 理由:由(1)知,闭合电路的电压恒为6 V,该用电器接在这个闭合电路中,通过的电流为 =1.2(A),大于此用电器允许通过的最大电流1 A,所以该用电器接在这个闭合电路中,会被烧毁.
感悟新知
知1-练
(3)由I= ,可知当I=4 时,R=1.5.
所以电阻应大于或等于1.5 Ω.
也可由 ≤4,即4R ≥ 6,解得
R≥1.5,所以电阻应大于或等于1.5 Ω.
感悟新知
知1-练
4-1. 一人站在平放在湿地上的木板上,当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对湿地的压强p(Pa) 与木板的面积S(m2)成反比例函数关系,如果人和木板对湿地的压力为600 N,回答下列问题:
感悟新知
知1-练
(1)写出p 与S 之间的函数解析式.
感悟新知
知1-练
(2)当木板面积为0.2 m2时,人和木板对湿地的压强是多少?
感悟新知
知1-练
(3)如果要求压强不超过6 000 Pa,木板面积至少要多大?
感悟新知
知1-练
(4)画出相应的函数图象.
解:函数图象如图所示.
感悟新知
知1-练
某商场出售一批进价为2 元的贺卡,在市场销售中发
现,此贺卡的日销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
例 5
日销售单价x/元 3 4 5 6
日销售量y/张 20 15 12 10
感悟新知
知1-练
解题秘方:紧扣“两个变量的对应值的乘积为同一常数,则这两个变量成反比例”求函数解析式;
(1)确定y 与x 之间的函数解析式;
感悟新知
知1-练
解:根据每组数据之积均为60,猜测y 与x 成反比例函数关系. 设y= (k ≠ 0),把x=3,y=20 代入y= 中,
得k=60,∴ y= (x ≥ 2).
把x=4,y=15;x=5,y=12;x=6,y=10 代入上式均成立.
∴ y 与x 之间的函数解析式为y= (x ≥ 2).
感悟新知
知1-练
解题秘方:紧扣“被除数一定,除数越大、商越小及被减数一定,减数越小、差越大”进行解答.
(2)设销售此贺卡的日销售利润为w 元,试求w 与x 之间的函数解析式. 若物价局规定该贺卡售价每张最高不超过10 元,请你求出日销售单价定为多少时,才能获得最大日销售利润.
感悟新知
知1-练
解:w=(x-2)y=(x-2)· =60- (2 ≤ x ≤ 10).
当x=10 时,w 有最大值.
即当日销售单价定为10 元时,才能获得最大日销售利润.
感悟新知
知1-练
5-1. 新能源汽车节能、环保,越来越受消费者喜爱,某汽车销售商推出分期付款购车促销活动,支付首付款后,余款要在30个月内结清, 不计算利息. 王先生在活动期间购买了价格为12 万元的汽车,
交了首付款后平均每个月付款y 万
元,x 个月结清. y 与x 的函数图象
如图所示,根据图象回答下列问题.
感悟新知
知1-练
(1)确定y 与x 的函数解析式,并求出首付款的数目.
感悟新知
知1-练
(2)王先生若用20 个月结清,平均每个月应付多少万元?
感悟新知
知1-练
(3)如果打算每个月付款不超过4 000 元,王先生至少要几个月才能结清余款?
课堂小结
实际问题与反比例函数
实际问题与反比例函数
步骤:审、设、列、写、解
常见类型
生活问题
工程问题
行程问题
跨学科问题
销售问题
26.2 实际问题与反比例函数
第26章 反比例函数
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
建立反比例函数模型解实际问题
知识点
建立反比例函数模型解实际问题
知1-讲
感悟新知
1
1. 在生活与生产中,如果某些问题的两个量成反比例关系,那么可以根据这种关系建立反比例函数模型,再利用反比例函数的有关知识解决实际问题.
特别提醒
利用反比例函数解决实际问题时应注意:
1.要理清题目中的常量与变量及其基本数量关系;
2.结合问题的实际意义,确定自变量的取值范围;
3.要熟练掌握反比例函数的意义、图象和性质.
知1-讲
感悟新知
运用反比例函数解决实际问题时常用的两种思路:
(1)通过问题提供的信息,明确变量之间的函数关系,设出相应的函数解析式,再根据题目条件确定函数解析式中的待定系数的值;
(2)已知反比例函数模型的解析式,运用反比例函数的图象及性质解决问题.
知1-讲
感悟新知
2. 用反比例函数解决实际问题的一般步骤
(1)审(2)设(3)列(4)写(5)解
感悟新知
知1-练
某地区上一年度每度电价格为0.8 元,年用电量为1亿度,本年度计划将电价调到0.55元~0.75元(不包括端点值).经测算,若电价调至x 元,则本年度新增用电量y(亿度)与(x-0.4)(元)成反比例,且当x=0.65 时,y=0.8.
例 1
感悟新知
知1-练
解题秘方:紧扣反比例关系用待定系数法设函数解析式求解.
(1)求y 与x 之间的函数解析式.
(2)若每度电的成本价为0.3 元,当电价调至0.72 元时,本年度电力部门的收益是多少元?
感悟新知
知1-练
解:(1)设y 与x 之间的函数解析式为y= (k ≠ 0).
∵当x=0.65 时,y=0.8,
∴ k=(x-0.4)y=(0.65-0.4)×0.8=0.2.
∴ y= ,
即y= (0.55 < x < 0.75).
感悟新知
知1-练
解:(2)当电价调至0.72 元时,新增用电量为
= 0.625(亿度),
则本年度用电量为1+0.625=1.625(亿度),
1.625 亿度=1.625×108 度.
∴(0.72-0.3)×1.625×108=6.825×107(元).
∴ 当电价调至0.72 元时, 本年度电力部门的收益是
6.825×107 元.
感悟新知
知1-练
1-1. 某户家庭用购电卡购买了2 000 度电, 若此户家庭平均每天的用电量为x(单位:度),这2 000 度电能够使用的天数为y(单位:天),则y 与x 的函数解析式为y= ____________(不要求写出自变量的取值范围).
感悟新知
知1-练
1-2. 如图是一蓄水池每小时的排水量V(m3)与排完蓄水池中的水所用时间t(h) 之间的函数关系图象, 若要5 h 排完蓄水池中的水, 则每小时的排水量为_______ m3.
9.6
感悟新知
知1-练
某机床加工一批机器零件,如果每小时加工30 个,
那么12 小时可以完成.
(1)设每小时加工x 个零件,所需时间为y 小时,写出y关于x 的函数解析式;
(2)若要在一个工作日(8 小时)内完成,每小时要比原来多加工几个零件?
例2
感悟新知
知1-练
解题秘方:紧扣工程问题中“工作总量、工作时间与工作效率”间的关系列式,变形即可求出函数解析式.
感悟新知
知1-练
解:(1)由题意得xy=30×12=360,
所以y 关于x 的函数解析式为y= (x > 0 且x 为整数).
(2)将y=8 代入y= 中,得8= , 解得x=45.
所以每小时要加工45 个. 45-30=15(个),
所以每小时要比原来多加工15 个零件.
感悟新知
知1-练
2-1. 某工厂生产化肥的总任务一定,平均每天的化肥产量y(吨)与完成总任务所需要的时间x(天)成反比例关系,如果平均每天生产化肥125 吨,那么完成总任务需要7 天.
感悟新知
知1-练
(1)求y 关于x 的函数解析式,并指出比例系数.
感悟新知
知1-练
(2)若要5 天完成总任务,则平均每天的化肥产量应达到多少?
感悟新知
知1-练
[中考·杭州] 方方驾驶小汽车匀速地从A 地行驶到B
地,行驶里程为480 km,设小汽车的行驶时间为t(单位:h),行驶速度为v(单位:km/h),且全程速度限定为不超过120 km/h.
例 3
感悟新知
知1-练
解题秘方:紧扣行程问题中路程一定时,速度与时间之间的关系,利用反比例函数的性质解决问题.
(1)求v 关于t 的函数解析式.
(2)方方上午8 点驾驶小汽车从A 地出发.
①方方需在当天12 点48 分至14 点(含12 点48 分和14 点)间到达B 地,求小汽车行驶速度v 的范围.
②方方能否在当天11 点30 分前到达B 地 说明理由.
感悟新知
知1-练
解:(1)∵ vt=480,且v ≤ 120,
∴ v 关于t 的函数解析式为v= (t ≥ 4).
感悟新知
知1-练
(2)① 8 点至12 点48 分的时间长为 h,8 点至14 点
的时间长为6 h,∴ ≤ t ≤ 6.
将t=6 代入v= 中,得v=80;将t= 代入v= 中,
得v=100. ∴小汽车行驶速度v 的范围为80 ≤ v ≤ 100.
感悟新知
知1-练
②方方不能在当天11 点30 分前到达B 地. 理由如下:
8 点至11 点30 分的时间长为 h,将t= 代入v= ,
得v= >120,超速.
故方方不能在当天11 点30 分前到达B 地.
感悟新知
知1-练
3-1. 小芳为响应“ 绿色出行, 低碳生活”,每天从家骑自行车去学校, 所需时间v(min)与骑车速度x(m/min)之间的反比例函数关系如图.
感悟新知
知1-练
(1)写出y 关于x 的函数解析式.
感悟新知
知1-练
(2)学校要求学生每天最晚7 时20 分到校,为了安全起见, 小芳的骑车速度最快不超过300 m/min,则她每天最晚什么时候出发?
解:当x=300时,y=8. 20-8=12(min).
∴ 她每天最晚7时12分出发.
感悟新知
知1-练
某闭合电路中,其电压恒定,电流I(A)与电阻R(Ω)成反比例函数关系,其图象如图26.2-1,根据图象回答下列问题.
例4
感悟新知
知1-练
(1)写出电流I 与电阻R 之间的函数解析式.
(2)如果一个用电器的电阻为5 Ω,其允许通过的最大电流是1 A,那么这个用电器接在这个闭合电路中,会不会被烧毁?请说明理由.
(3)若允许通过的电流不超过4 A,那么电阻的取值应该控制在什么范围?
感悟新知
知1-练
解题秘方:紧扣“电压恒定,电流与电阻成反比例函数关系”,用待定系数法求反比例函数解析式,再结合函数解析式求解其他问题.
感悟新知
知1-练
解:(1)设I= (k ≠ 0),由图象过点(3,2),得2= , 解得k=6.
所以电流I 与电阻R 之间的函数解析式为I= .
感悟新知
知1-练
(2)会被烧毁. 理由:由(1)知,闭合电路的电压恒为6 V,该用电器接在这个闭合电路中,通过的电流为 =1.2(A),大于此用电器允许通过的最大电流1 A,所以该用电器接在这个闭合电路中,会被烧毁.
感悟新知
知1-练
(3)由I= ,可知当I=4 时,R=1.5.
所以电阻应大于或等于1.5 Ω.
也可由 ≤4,即4R ≥ 6,解得
R≥1.5,所以电阻应大于或等于1.5 Ω.
感悟新知
知1-练
4-1. 一人站在平放在湿地上的木板上,当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对湿地的压强p(Pa) 与木板的面积S(m2)成反比例函数关系,如果人和木板对湿地的压力为600 N,回答下列问题:
感悟新知
知1-练
(1)写出p 与S 之间的函数解析式.
感悟新知
知1-练
(2)当木板面积为0.2 m2时,人和木板对湿地的压强是多少?
感悟新知
知1-练
(3)如果要求压强不超过6 000 Pa,木板面积至少要多大?
感悟新知
知1-练
(4)画出相应的函数图象.
解:函数图象如图所示.
感悟新知
知1-练
某商场出售一批进价为2 元的贺卡,在市场销售中发
现,此贺卡的日销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
例 5
日销售单价x/元 3 4 5 6
日销售量y/张 20 15 12 10
感悟新知
知1-练
解题秘方:紧扣“两个变量的对应值的乘积为同一常数,则这两个变量成反比例”求函数解析式;
(1)确定y 与x 之间的函数解析式;
感悟新知
知1-练
解:根据每组数据之积均为60,猜测y 与x 成反比例函数关系. 设y= (k ≠ 0),把x=3,y=20 代入y= 中,
得k=60,∴ y= (x ≥ 2).
把x=4,y=15;x=5,y=12;x=6,y=10 代入上式均成立.
∴ y 与x 之间的函数解析式为y= (x ≥ 2).
感悟新知
知1-练
解题秘方:紧扣“被除数一定,除数越大、商越小及被减数一定,减数越小、差越大”进行解答.
(2)设销售此贺卡的日销售利润为w 元,试求w 与x 之间的函数解析式. 若物价局规定该贺卡售价每张最高不超过10 元,请你求出日销售单价定为多少时,才能获得最大日销售利润.
感悟新知
知1-练
解:w=(x-2)y=(x-2)· =60- (2 ≤ x ≤ 10).
当x=10 时,w 有最大值.
即当日销售单价定为10 元时,才能获得最大日销售利润.
感悟新知
知1-练
5-1. 新能源汽车节能、环保,越来越受消费者喜爱,某汽车销售商推出分期付款购车促销活动,支付首付款后,余款要在30个月内结清, 不计算利息. 王先生在活动期间购买了价格为12 万元的汽车,
交了首付款后平均每个月付款y 万
元,x 个月结清. y 与x 的函数图象
如图所示,根据图象回答下列问题.
感悟新知
知1-练
(1)确定y 与x 的函数解析式,并求出首付款的数目.
感悟新知
知1-练
(2)王先生若用20 个月结清,平均每个月应付多少万元?
感悟新知
知1-练
(3)如果打算每个月付款不超过4 000 元,王先生至少要几个月才能结清余款?
课堂小结
实际问题与反比例函数
实际问题与反比例函数
步骤:审、设、列、写、解
常见类型
生活问题
工程问题
行程问题
跨学科问题
销售问题
