2022-2023学年人教版数学九年级上册24.1.4 圆周角 导学案(无答案)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册24.1.4 圆周角 导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 208.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:33:08 | ||
图片预览


文档简介
24.1.4圆周角
【第一课时】
【学习目标】
1.了解圆周角的概念,理解圆周角的定理,理解圆周角定理的推论。
2.熟练掌握圆周角的定理及其推理的灵活运用。
【学习重难点】
圆周角的定理、圆周角定理的推导及运用它们解题;证明圆周角的定理。
【学习过程】
一、合作探究。
1.归纳得出结论,顶点在 ,并且两边 的角叫做圆周角。
2.强调条件:① ,② 。
3.如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC所对的圆心角、圆周角,求出图(1)(2)(3)中∠BAC的度数。
通过计算发现:∠BAC=_____∠BOC
即,
。
通过上述讨论发现: 即圆周角的定理。
定理的推理1:(1)在同圆或等圆中,同弧或等弧所对的 相等,都等于这条弧所对的 ,表达式: 。
(2)在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定 。
表达式: 。
学习小结。
圆周角的性质:①一条弧所对的圆周角等于该弧所对的圆心角的 。②在同一个圆中,同弧或等弧所对的圆周角 ,都等于这条弧所对的圆心角的 ;在同圆或等圆中,相等的圆周角所对的弧相等。
【第二课时】
【学习目标】
1.掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径。
2.经历圆周角性质的过程,培养学生分析问题和解决问题的能力。
3.激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活。
【学习重难点】
掌握圆周角的性质,圆周角性质的应用。
【学习过程】
一、预习导学。
如图,点A、B、C、D在⊙O上,若∠BAC=40°,则∠BOC= °,理由是 。
二、自主学习。
归纳自己总结的结论:
(1) 。
(2) 。
注意:
(1)这里所对的角、90°的角必须是圆周角;
(2)直径所对的圆周角是直角,在圆的有关问题中经常遇到,同学们要高度重视。
三、学习总结。
1.两条性质: 。
2.直径所对的圆周角是直角是圆中常见辅助线。
【第三课时】
【学习目标】
1.了解圆内接四边形的概念。
2.理解圆内接四边形的性质,并会运用其性质分析解决有关问题。
【学习重难点】
圆内接四边形的性质和其应用,圆内接四边形的性质探究。
【学习过程】
一、复习旧知。
1.在在同圆或等圆中,同弧或等弧所对圆周角 。反过来,相等的圆周角所对的弧 ,同弧或等弧所对圆周角是其所对的圆心角的 。
2.半圆或直径所对的圆周角都是 °,90°的圆周角所对的弦是圆是 。
二、合作探究。
1.合作学习.
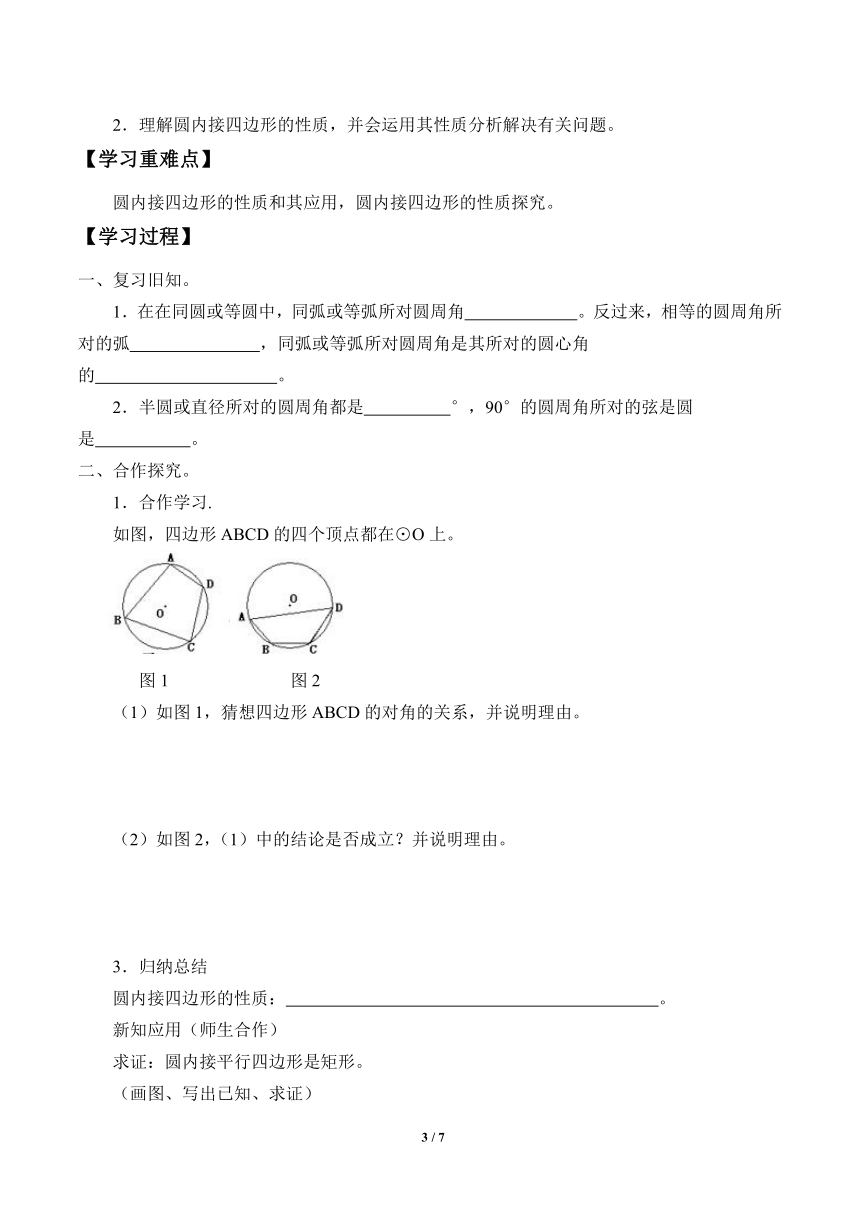
如图,四边形ABCD的四个顶点都在⊙O上。
图1 图2
(1)如图1,猜想四边形ABCD的对角的关系,并说明理由。
(2)如图2,(1)中的结论是否成立?并说明理由。
3.归纳总结
圆内接四边形的性质: 。
新知应用(师生合作)
求证:圆内接平行四边形是矩形。
(画图、写出已知、求证)
巩固练习
一、单选题
1.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
A.25° B.35° C.45° D.65°
2.如图,AB是的直径,点C,D,E是上的点,其中点C,D在AB下方,点E在AB上方.则的度数为( )
A.60° B.45° C.30° D.90°
3.如图,点在上,,则( )
A. B. C. D.
4.若四边形ABCD是⊙O的内接四边形,∠A:∠C=1:2,则∠C=( )
A.120° B.130° C.140° D.150°
5.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于,两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A.1.0厘米/分 B.0.8厘米/分 C.12厘米/分 D.1.4厘米/分
二、填空题
6.如图,是的外接圆,,是上的一点,则等于________.
7.如图,,,是上的三个点,四边形是平行四边形,连接,,若,则_____.
8.如图,已知的半径为2,内接于,,则__________.
三、解答题
9.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连接AC,OC,BC.
(1)求证:∠1=∠2;
(2)若,求⊙O的半径的长.
10.如图,两个圆都以点O为圆心,大圆的弦交小圆于两点.求证:.
11.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
1 / 5
【第一课时】
【学习目标】
1.了解圆周角的概念,理解圆周角的定理,理解圆周角定理的推论。
2.熟练掌握圆周角的定理及其推理的灵活运用。
【学习重难点】
圆周角的定理、圆周角定理的推导及运用它们解题;证明圆周角的定理。
【学习过程】
一、合作探究。
1.归纳得出结论,顶点在 ,并且两边 的角叫做圆周角。
2.强调条件:① ,② 。
3.如图,AB为⊙O的直径,∠BOC、∠BAC分别是BC所对的圆心角、圆周角,求出图(1)(2)(3)中∠BAC的度数。
通过计算发现:∠BAC=_____∠BOC
即,
。
通过上述讨论发现: 即圆周角的定理。
定理的推理1:(1)在同圆或等圆中,同弧或等弧所对的 相等,都等于这条弧所对的 ,表达式: 。
(2)在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定 。
表达式: 。
学习小结。
圆周角的性质:①一条弧所对的圆周角等于该弧所对的圆心角的 。②在同一个圆中,同弧或等弧所对的圆周角 ,都等于这条弧所对的圆心角的 ;在同圆或等圆中,相等的圆周角所对的弧相等。
【第二课时】
【学习目标】
1.掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径。
2.经历圆周角性质的过程,培养学生分析问题和解决问题的能力。
3.激发学生探索新知的兴趣,培养刻苦学习的精神,进一步体会数学源于生活并用于生活。
【学习重难点】
掌握圆周角的性质,圆周角性质的应用。
【学习过程】
一、预习导学。
如图,点A、B、C、D在⊙O上,若∠BAC=40°,则∠BOC= °,理由是 。
二、自主学习。
归纳自己总结的结论:
(1) 。
(2) 。
注意:
(1)这里所对的角、90°的角必须是圆周角;
(2)直径所对的圆周角是直角,在圆的有关问题中经常遇到,同学们要高度重视。
三、学习总结。
1.两条性质: 。
2.直径所对的圆周角是直角是圆中常见辅助线。
【第三课时】
【学习目标】
1.了解圆内接四边形的概念。
2.理解圆内接四边形的性质,并会运用其性质分析解决有关问题。
【学习重难点】
圆内接四边形的性质和其应用,圆内接四边形的性质探究。
【学习过程】
一、复习旧知。
1.在在同圆或等圆中,同弧或等弧所对圆周角 。反过来,相等的圆周角所对的弧 ,同弧或等弧所对圆周角是其所对的圆心角的 。
2.半圆或直径所对的圆周角都是 °,90°的圆周角所对的弦是圆是 。
二、合作探究。
1.合作学习.
如图,四边形ABCD的四个顶点都在⊙O上。
图1 图2
(1)如图1,猜想四边形ABCD的对角的关系,并说明理由。
(2)如图2,(1)中的结论是否成立?并说明理由。
3.归纳总结
圆内接四边形的性质: 。
新知应用(师生合作)
求证:圆内接平行四边形是矩形。
(画图、写出已知、求证)
巩固练习
一、单选题
1.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CAB=65°,则∠ADC的度数为( )
A.25° B.35° C.45° D.65°
2.如图,AB是的直径,点C,D,E是上的点,其中点C,D在AB下方,点E在AB上方.则的度数为( )
A.60° B.45° C.30° D.90°
3.如图,点在上,,则( )
A. B. C. D.
4.若四边形ABCD是⊙O的内接四边形,∠A:∠C=1:2,则∠C=( )
A.120° B.130° C.140° D.150°
5.如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于,两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A.1.0厘米/分 B.0.8厘米/分 C.12厘米/分 D.1.4厘米/分
二、填空题
6.如图,是的外接圆,,是上的一点,则等于________.
7.如图,,,是上的三个点,四边形是平行四边形,连接,,若,则_____.
8.如图,已知的半径为2,内接于,,则__________.
三、解答题
9.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,连接AC,OC,BC.
(1)求证:∠1=∠2;
(2)若,求⊙O的半径的长.
10.如图,两个圆都以点O为圆心,大圆的弦交小圆于两点.求证:.
11.如图,△ABC内接于⊙O,∠A = 30°,过圆心O作OD⊥BC,垂足为D.若⊙O的半径为6,求OD的长.
1 / 5
同课章节目录
