探索勾股定理[上学期]

课件20张PPT。第二课时探索勾股定理第一课时翠园初中倪旋探索勾股定理1 勾股定理有着悠久的历史，古巴比伦和古代中国人看出了这个关系；古希腊的毕达哥拉斯学派首先证明了这个关系。很多具有古老文化的民族和国家都会说：我们首先认识的数学定理是
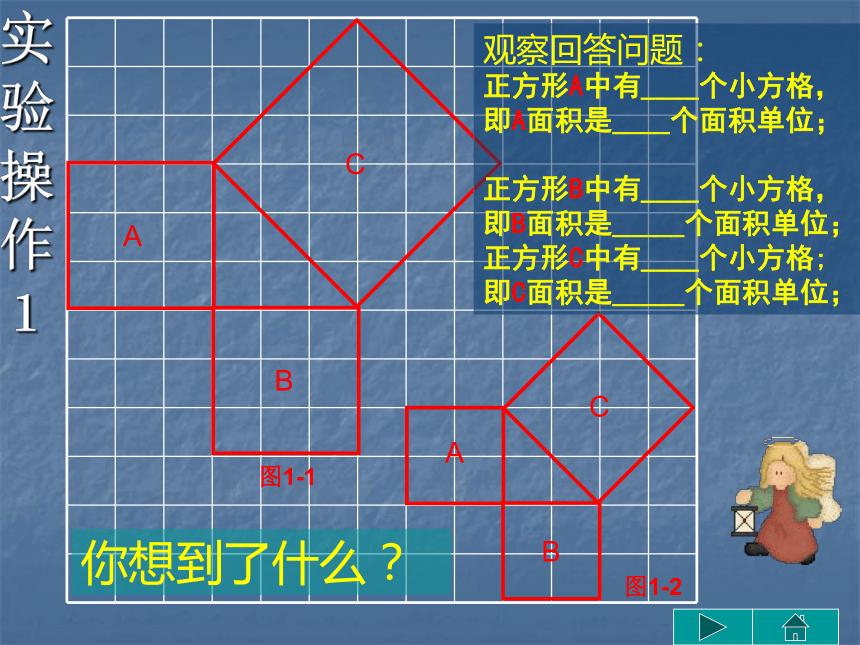
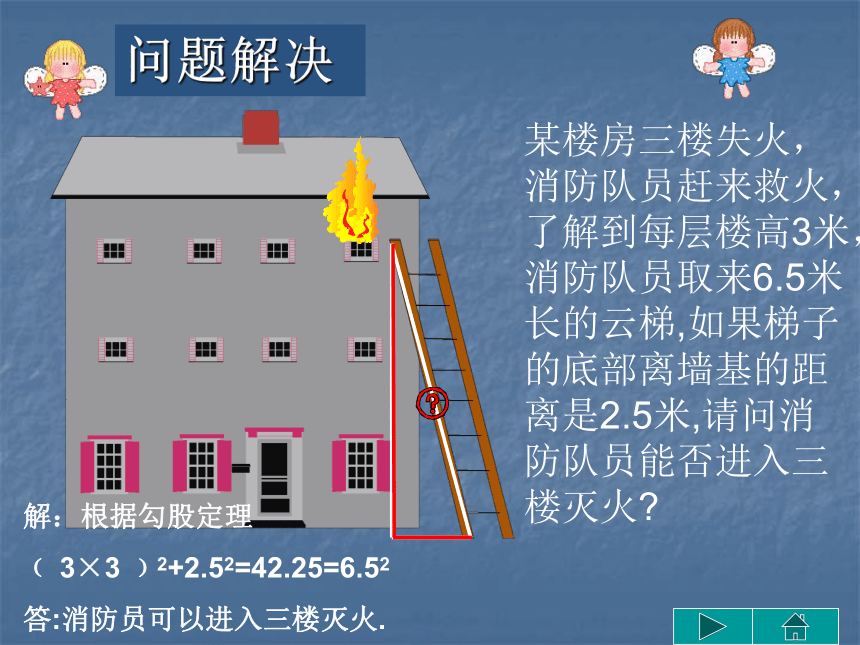
勾股定理。提出问题实验操作归纳验证实际运用解决问题小 结返回首页某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 提出问题AACBBC图1-1 图1-2 实验操作１观察回答问题：
正方形A中有____个小方格，
即A面积是____个面积单位；
正方形B中有____个小方格，
即B面积是_____个面积单位；
正方形C中有____个小方格;
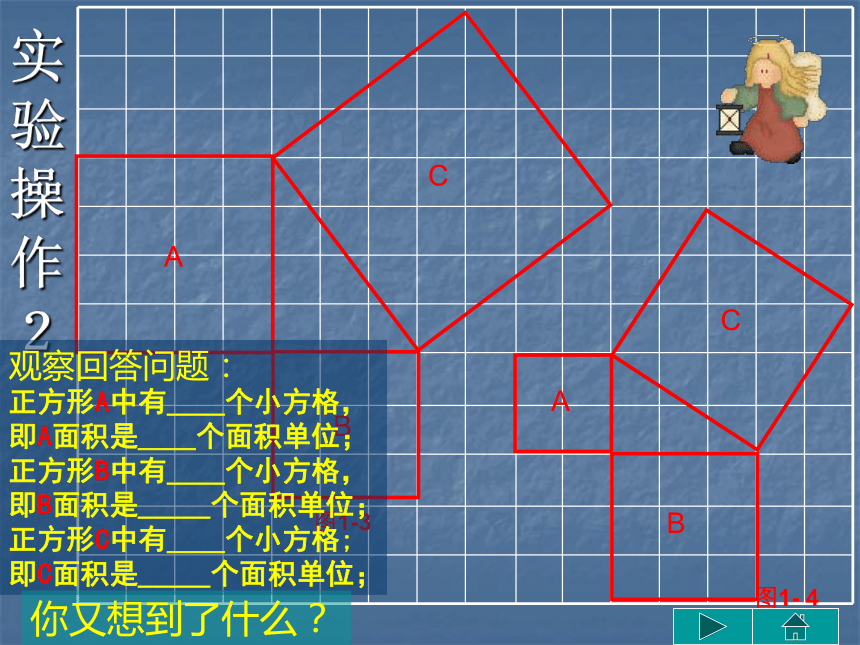
即C面积是_____个面积单位；你想到了什么？AACBBC图1-3 图1- 4 实验操作２观察回答问题：
正方形A中有____个小方格，
即A面积是____个面积单位；
正方形B中有____个小方格，
即B面积是_____个面积单位；
正方形C中有____个小方格;
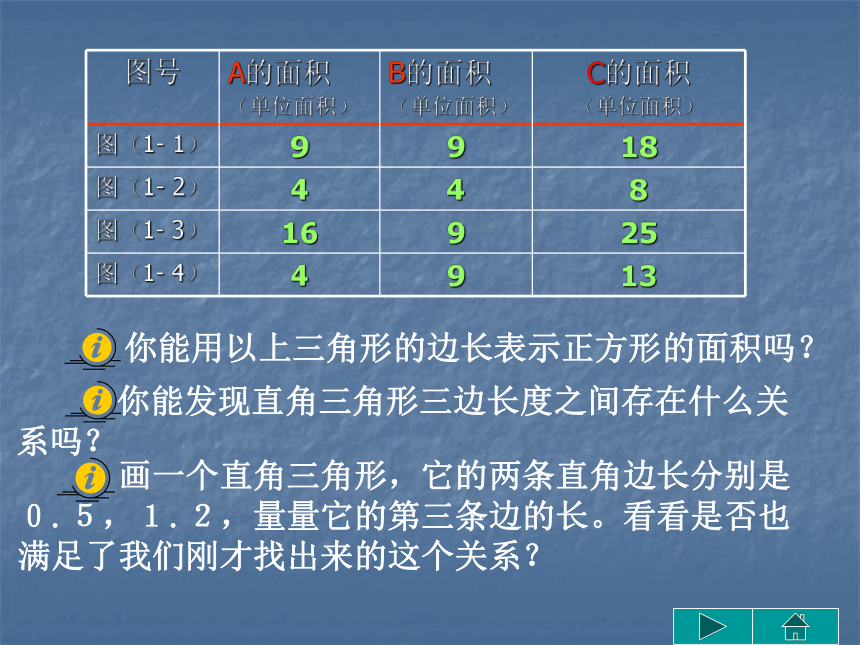
即C面积是_____个面积单位；你又想到了什么？　　　画一个直角三角形，它的两条直角边长分别是０.５，１.２，量量它的第三条边的长。看看是否也满足了我们刚才找出来的这个关系？　　　你能用以上三角形的边长表示正方形的面积吗？　　　你能发现直角三角形三边长度之间存在什么关系吗？勾股定理:如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2。勾股弦 我国古代把
直角三角形
中较短的直
角边称为勾， 较长的直角
边称为股，斜边称为弦。即直角三角形两直角边的平方和等于斜边的平方。问题解决某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队员能否进入三楼灭火? 解：根据勾股定理
﹙ 3×3 ﹚2+2.52=42.25=6.52
答:消防员可以进入三楼灭火.小明妈妈买了一部 29 英寸(74厘米)的电视机,小明量了屏幕
的长是 58 厘米宽是 46 厘米,他觉得一定哪里搞错了?你能帮
助小明解释这是为什么吗?
想一想582=3364 462=2116(1英寸=2.54厘米)课堂小结回忆本节课所学内容，谈谈学习感想。布置作业 课本P6习题1.1 1，2，3，4
补充题：在下图中尽量多地找出线段之间的关系。ADBC探索勾股定理2 验证定理实践出真知议一议巩固知识返回首页小 结问题一 ：
（1）在一张纸上画4个如图的直角三角形，并把它们剪下来。
（2）用这4个直角三角形摆一摆，看看能否得到一个含有以斜边C为边长的正方形，并利用它说明勾股定理。
（3）若利用这4个直角三角形拼出了如图，你能利用两种方法表示大正方形的面积吗？c问题二：除了上面的拼法外，还可以怎样拼可以得到一个含有以斜边c为边长的正方形？大正方形的面积可以表示为__________,又可以表示为___________.对比两种表示方法，你能从中得到勾股定理吗？（a+b)22ab+c2实践出真知飞机在天空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方
4000米处,过了20秒,飞机距离这个男孩头顶5000米,飞机每时飞行
多少千米?
20秒4000米5000米 议
一
议用数格子的方法
判断图中三角形
的三边长是否满
足 a2+b2=c2.cab 议
一
议cab用数格子的方法
判断图中三角形
的三边长是否满
足 a2+b2=c2.练习1：已知如图，等腰三角形ABC的底边为30cm，腰为25cm.
(1)求高AD的长。
(2)求S△ABC注：等腰三角形三线合一巩固知识练习2：判断下列解题过程是否正确。
在直角三角形ABC中，∠B=900 a=3,b=4,求c.解：由勾股定理得：
a2+b2=c2
∴ c2=32+42=25
c=5 作业: 1课本第9页习题 1.2 1，2
2收集有关勾股定理的证明的资料，与同伴分享 通过这节课的学习，你有什么收获呢？小结：返回首页谢谢返回首页