2022-2023学年 北师大版八年级数学上册4.4 一次函数的应用 同步练习 (word版 含答案)
文档属性
| 名称 | 2022-2023学年 北师大版八年级数学上册4.4 一次函数的应用 同步练习 (word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览




文档简介
北师大版八上 4.4 一次函数的应用
一、选择题(共11小题)
1. 已知 ,当函数值为 时,自变量 为
A. B. C. D.
2. 下列各点,在一次函数 的图象上的是
A. B. C. D.
3. 梅凯种子公司以一定价格销售“黄金 1 号”玉米种子,如果一次购买 千克以上(不含 千克)的种子,超过 千克的那部分种子的价格将打折,并依此得到付款金额 (单位:元)与一次购买种子数量 (单位:千克)之间的函数关系如图所示,下列四种说法:
① 一次购买种子数量不超过 千克时,销售价格为 元/千克;
② 一次购买 千克种子时,付款金额为 元;
③ 一次购买 千克以上种子时,超过 千克的那部分种子的价格打五折;
④ 一次购买 千克种子比分两次购买且每次购买 千克种子少花 元钱.
其中正确的个数是
A. 个 B. 个 C. 个 D. 个
4. 已知直线 : 与直线 : 在第三象限交于点 ,若直线 与 轴的交点为 ,则 的取值范围是
A. B. C. D.
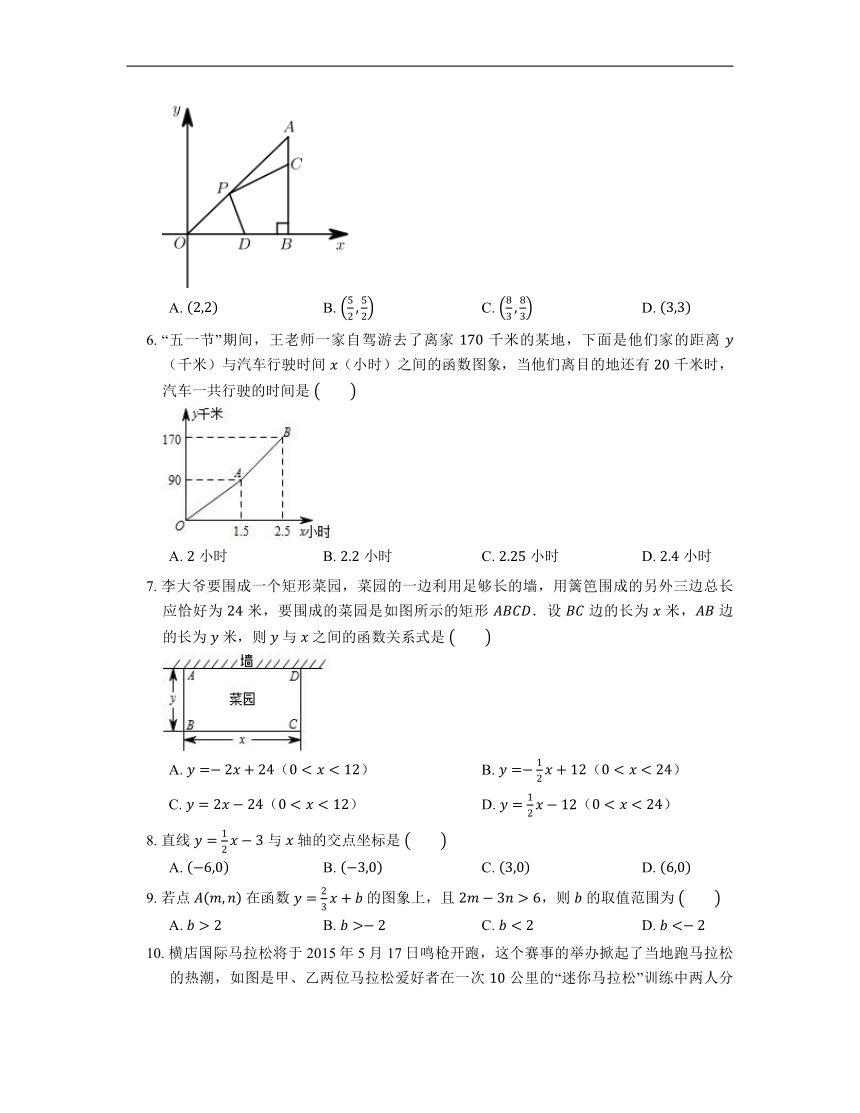
5. 如图,在 中,,,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为
A. B. C. D.
6. “五一节”期间,王老师一家自驾游去了离家 千米的某地,下面是他们家的距离 (千米)与汽车行驶时间 (小时)之间的函数图象,当他们离目的地还有 千米时,汽车一共行驶的时间是
A. 小时 B. 小时 C. 小时 D. 小时
7. 李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为 米,要围成的菜园是如图所示的矩形 .设 边的长为 米, 边的长为 米,则 与 之间的函数关系式是
A. () B. ()
C. () D. ()
8. 直线 与 轴的交点坐标是
A. B. C. D.
9. 若点 在函数 的图象上,且 ,则 的取值范围为
A. B. C. D.
10. 横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次 公里的“迷你马拉松”训练中两人分别跑的路程 (公里)与时间 (分钟)的函数关系图象,他们同时出发,乙在 分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是 公里/分;(2)乙在冲刺阶段的速度 公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距 公里的次数是 次.以上说法正确的个数是
A. B. C. D.
11. 如图,正方形 的边长为 ,点 为正方形边上一动点,若点 从点 出发沿 匀速运动一周.设点 走过的路程为 , 的面积为 ,则下列图象能大致反映 与 的函数关系的是
A. B.
C. D.
二、填空题(共6小题)
12. 直线 与 轴的交点坐标为 .
13. 如图是某工程队在“村村通”工程中,修筑的公路长度 (米)与时间 (天)之间的关系图象.根据图象提供的信息,可知该公路的长度是 米.
14. 已知一次函数 ,当 时,,则一次函数的表达式为 .
15. 若一个函数图象经过点 ,,则关于此函数的说法:
①该函数可能是一次函数;
②点 , 不可能同时在该函数图象上;
③函数值 一定随自变量 的增大而减小;
④可能存在自变量 的某个取值范围,在这个范围内函数值 随自变量 增大而增大.
所有正确结论的序号是 .
16. 已知直线 与 轴的交点在 和 之间(包括 , 两点),直线 与 轴交于点 ,则 的取值范围为 .
17. 已知直线 :( 是不为零的自然数).当 时,直线 : 与 轴和 轴分别交于点 和 ,设 ,(其中 是平面直角坐标系的原点)的面积为 ;当 时,直线 : 与 轴和 轴分别交于点 和 ,设 的面积为 ;…依此类推,直线 与 轴和 轴分别交于点 和 ,设 的面积为 .则 的面积 等于 ; 的值是 .
三、解答题(共6小题)
18. 根据下列条件,确定直线的表达式:
(1)直线经过 , 两点
(2)直线经过点 ,它与 轴的交点的横坐标为 .
19. 分别画出下列函数的图象:
(1).
(2).
(3).
(4).
20. 已知一次函数 的自变量的取值范围是 ,相应的函数值的取值范围是 ,求这个一次函数的解析式.
21. 库尔勒某乡 , 两村盛产香梨, 村有香梨 吨, 村有香梨 吨,现将这些香梨运到 , 两个冷藏仓库.已知 仓库可储存 吨, 仓库可储存 吨,从 村运往 , 两处的费用分别为每吨 元和 元;从 村运往 , 两处的费用分别为每吨 元和 元,设从 村运往 仓库的香梨为 吨,, 两村运送香梨往两仓库的运输费用分别为 元、 元.
(1)请填写下表,并求出 , 与 之间的函数表达式;
(2)当 为何值时, 村的运费较少
(3)请问怎样调运,才能使两村的运费之和最小 求出最小值.
22. 已知直线 : 和直线 : ,求两条直线 和 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
23. 在某旧城区改造中,有一部分楼盘要对外销售,某楼盘共三十层,销售价格如下:第六层楼房的售价为 元/ ,从第六层起,每下降一层,每平方米售价下降 元,每上升一层,每平方米售价提高 元,直到第二十六层,从第二十七层起,每上升一层降价 元出售.假设每套楼房的面积均为 ,若购买者一次性付清所有房款,则开发商有两种优惠方案:
方案一:降价 ,另外每套楼房赠送 元装修基金;
方案二:降价 ,没有其他赠送.
(1)写出售价 (元/ )与楼层 ( 且 为整数)之间的函数关系式;
(2)某人想一次性付清一套二十层住房的房款,请你帮忙算一算哪种方案更优惠.
答案
1. B
2. D
3. D
【解析】由图象可知,当 时,销售单价为 (元/千克),故 ① 正确;
当 时,超过 千克的单价是 (元/千克),故相对之前的价格打了五折,故 ③ 正确;
当一次购买 千克种子时应付款 (元),故 ② 正确;
一次购买 千克种子时应付款 (元),而分两次购买每次购买 千克种子应付款 (元),比一次购买 千克种子贵了 元,故 ④ 正确,所以正确的个数有 个.
4. D 【解析】 直线 与 轴的交点为 ,
,
,
直线 : 与 轴的交点坐标为 ,
若直线 与 轴的交点为 ,
则 与 轴交点 在原点和点 之间,
即:,
解得:.
5. C
【解析】 在 中,,,
,,
,点 为 的中点,
,,
,,
作 关于直线 的对称点 ,连接 交 于 ,
则此时,四边形 周长最小,,
直线 的解析式为 ,
设直线 的解析式为 ,
解得:
直线 的解析式为 ,
解 得
.
6. C
【解析】过 的直线解析式为 .当他们离目的地还有 千米时,即 ,此时 .
7. B
【解析】由题意得 ,即 ,
与 之间的函数解析式为 .
又 ,
,
,
与 之间的函数解析式为 ().
8. D
9. D
10. D
【解析】甲前半程的速度是:(公里/分),故(1)正确;
乙在冲刺阶段的速度为:(公里/分),故(2)正确;
根据函数图象可知,在前半程甲的函数图象在乙的函数图象上方,所以在前半程甲一直领先于乙,故(3)正确;
当 时,,
当 时,,
当 时,,
当 时,,
甲与乙刚好相距 公里时,即,
,解得:,
,解得:,
,解得:,
,解得:,
甲与乙刚好相距 公里的次数是 次,
故(4)正确;
11. D
【解析】由题意可知:当 在 上时,这时构不成三角形,此时 ,
当 在 上时, 的面积在增大, 与 重合时最大为 ,此时 ;
当 在 上时, 的面积不变等于 ,此时 ;
当 在 上时, 的面积在减小,此时 .
12.
13.
【解析】设 时,函数解析式为 ,
,,
解得 ,,
,
当 时,.
14. 或
【解析】当 时, 随 的增大而增大,
直线过点 ,,则 解得
一次函数的表达式为 ;
当 时, 随 的增大而减小,
直线过点 ,,
则
解得
一次函数的表达式为 .
故一次函数的表达式为 或 .
15. ①②④
【解析】①因为一次函数的图象是一条直线,由两点确定一条直线,故该函数可能是一次函数,故正确;
②由函数的定义:在一个变化过程中,有两个变量 ,,对于 的每一个取值, 都有唯一确定的值与之对应,则 是 的函数, 叫自变量,所以点 , 不可能同时在该函数图象上,故正确;
③因为函数关系不确定,所以函数值 不一定一直随自变量 的增大而减小,故错误;
④可能存在自变量 的某个取值范围,在这个范围内函数值 随自变量 增大而增大,故正确.
16.
【解析】 与 轴的交点坐标为 ,
由题知 ,
与 轴的交点为 ,
易知 ,
,
,
.
17. ,
【解析】: 与 轴和 轴分别交于点 和 ,,
: 与 轴和 轴分别交于点 ,,,
与 轴和 轴分别交于点 ,,,
与 轴和 轴分别交于点 ,,,
: 与 轴和 轴分别交于点 ,,.
18. (1) .
(2) .
19. (1)
(2)
(3)
(4)
20. 分两种情况:
①当 时,把 ,;, 分别代入一次函数的解析式 中,
得 解得
则这个函数的解析式是 .
②当 时,把 ,;, 分别代入一次函数的解析式 中,
得 解得
则这个函数的解析式是 .
故这个函数的解析式是 或 .
21. (1) 填表如下:
由题意,得 ;.
(2) 对于 ,
,
随 的增大而减小.
当 吨时, 最小,其最小值为 (元).
(3) 设两村的运费之和为 ,
则 .
,
随着 的增大而增大.
当 时, 有最小值, 最小值为 元.
按该方案调运,两村的运费之和最小,最小值为 元.
22. 解:由题意得,
解得,
∴ 直线 和直线 的交点坐标是
交点 落在平面直角坐标系的第四象限上.
23. (1) 当 ( 为整数)时,;
当 ( 为整数)时,;
当 ( 为整数)时,.
(2) 当 时,,
总价为 元,
方案一需付费 元.
方案二需付费 元.
当 时,;
当 时,;
当 时,.
答:当装修基金为 元时,两种方案均可;
当装修基金小于 元时,选择方案二;
当装修基金大于 元时,选择方案一.
一、选择题(共11小题)
1. 已知 ,当函数值为 时,自变量 为
A. B. C. D.
2. 下列各点,在一次函数 的图象上的是
A. B. C. D.
3. 梅凯种子公司以一定价格销售“黄金 1 号”玉米种子,如果一次购买 千克以上(不含 千克)的种子,超过 千克的那部分种子的价格将打折,并依此得到付款金额 (单位:元)与一次购买种子数量 (单位:千克)之间的函数关系如图所示,下列四种说法:
① 一次购买种子数量不超过 千克时,销售价格为 元/千克;
② 一次购买 千克种子时,付款金额为 元;
③ 一次购买 千克以上种子时,超过 千克的那部分种子的价格打五折;
④ 一次购买 千克种子比分两次购买且每次购买 千克种子少花 元钱.
其中正确的个数是
A. 个 B. 个 C. 个 D. 个
4. 已知直线 : 与直线 : 在第三象限交于点 ,若直线 与 轴的交点为 ,则 的取值范围是
A. B. C. D.
5. 如图,在 中,,,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为
A. B. C. D.
6. “五一节”期间,王老师一家自驾游去了离家 千米的某地,下面是他们家的距离 (千米)与汽车行驶时间 (小时)之间的函数图象,当他们离目的地还有 千米时,汽车一共行驶的时间是
A. 小时 B. 小时 C. 小时 D. 小时
7. 李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为 米,要围成的菜园是如图所示的矩形 .设 边的长为 米, 边的长为 米,则 与 之间的函数关系式是
A. () B. ()
C. () D. ()
8. 直线 与 轴的交点坐标是
A. B. C. D.
9. 若点 在函数 的图象上,且 ,则 的取值范围为
A. B. C. D.
10. 横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次 公里的“迷你马拉松”训练中两人分别跑的路程 (公里)与时间 (分钟)的函数关系图象,他们同时出发,乙在 分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是 公里/分;(2)乙在冲刺阶段的速度 公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距 公里的次数是 次.以上说法正确的个数是
A. B. C. D.
11. 如图,正方形 的边长为 ,点 为正方形边上一动点,若点 从点 出发沿 匀速运动一周.设点 走过的路程为 , 的面积为 ,则下列图象能大致反映 与 的函数关系的是
A. B.
C. D.
二、填空题(共6小题)
12. 直线 与 轴的交点坐标为 .
13. 如图是某工程队在“村村通”工程中,修筑的公路长度 (米)与时间 (天)之间的关系图象.根据图象提供的信息,可知该公路的长度是 米.
14. 已知一次函数 ,当 时,,则一次函数的表达式为 .
15. 若一个函数图象经过点 ,,则关于此函数的说法:
①该函数可能是一次函数;
②点 , 不可能同时在该函数图象上;
③函数值 一定随自变量 的增大而减小;
④可能存在自变量 的某个取值范围,在这个范围内函数值 随自变量 增大而增大.
所有正确结论的序号是 .
16. 已知直线 与 轴的交点在 和 之间(包括 , 两点),直线 与 轴交于点 ,则 的取值范围为 .
17. 已知直线 :( 是不为零的自然数).当 时,直线 : 与 轴和 轴分别交于点 和 ,设 ,(其中 是平面直角坐标系的原点)的面积为 ;当 时,直线 : 与 轴和 轴分别交于点 和 ,设 的面积为 ;…依此类推,直线 与 轴和 轴分别交于点 和 ,设 的面积为 .则 的面积 等于 ; 的值是 .
三、解答题(共6小题)
18. 根据下列条件,确定直线的表达式:
(1)直线经过 , 两点
(2)直线经过点 ,它与 轴的交点的横坐标为 .
19. 分别画出下列函数的图象:
(1).
(2).
(3).
(4).
20. 已知一次函数 的自变量的取值范围是 ,相应的函数值的取值范围是 ,求这个一次函数的解析式.
21. 库尔勒某乡 , 两村盛产香梨, 村有香梨 吨, 村有香梨 吨,现将这些香梨运到 , 两个冷藏仓库.已知 仓库可储存 吨, 仓库可储存 吨,从 村运往 , 两处的费用分别为每吨 元和 元;从 村运往 , 两处的费用分别为每吨 元和 元,设从 村运往 仓库的香梨为 吨,, 两村运送香梨往两仓库的运输费用分别为 元、 元.
(1)请填写下表,并求出 , 与 之间的函数表达式;
(2)当 为何值时, 村的运费较少
(3)请问怎样调运,才能使两村的运费之和最小 求出最小值.
22. 已知直线 : 和直线 : ,求两条直线 和 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
23. 在某旧城区改造中,有一部分楼盘要对外销售,某楼盘共三十层,销售价格如下:第六层楼房的售价为 元/ ,从第六层起,每下降一层,每平方米售价下降 元,每上升一层,每平方米售价提高 元,直到第二十六层,从第二十七层起,每上升一层降价 元出售.假设每套楼房的面积均为 ,若购买者一次性付清所有房款,则开发商有两种优惠方案:
方案一:降价 ,另外每套楼房赠送 元装修基金;
方案二:降价 ,没有其他赠送.
(1)写出售价 (元/ )与楼层 ( 且 为整数)之间的函数关系式;
(2)某人想一次性付清一套二十层住房的房款,请你帮忙算一算哪种方案更优惠.
答案
1. B
2. D
3. D
【解析】由图象可知,当 时,销售单价为 (元/千克),故 ① 正确;
当 时,超过 千克的单价是 (元/千克),故相对之前的价格打了五折,故 ③ 正确;
当一次购买 千克种子时应付款 (元),故 ② 正确;
一次购买 千克种子时应付款 (元),而分两次购买每次购买 千克种子应付款 (元),比一次购买 千克种子贵了 元,故 ④ 正确,所以正确的个数有 个.
4. D 【解析】 直线 与 轴的交点为 ,
,
,
直线 : 与 轴的交点坐标为 ,
若直线 与 轴的交点为 ,
则 与 轴交点 在原点和点 之间,
即:,
解得:.
5. C
【解析】 在 中,,,
,,
,点 为 的中点,
,,
,,
作 关于直线 的对称点 ,连接 交 于 ,
则此时,四边形 周长最小,,
直线 的解析式为 ,
设直线 的解析式为 ,
解得:
直线 的解析式为 ,
解 得
.
6. C
【解析】过 的直线解析式为 .当他们离目的地还有 千米时,即 ,此时 .
7. B
【解析】由题意得 ,即 ,
与 之间的函数解析式为 .
又 ,
,
,
与 之间的函数解析式为 ().
8. D
9. D
10. D
【解析】甲前半程的速度是:(公里/分),故(1)正确;
乙在冲刺阶段的速度为:(公里/分),故(2)正确;
根据函数图象可知,在前半程甲的函数图象在乙的函数图象上方,所以在前半程甲一直领先于乙,故(3)正确;
当 时,,
当 时,,
当 时,,
当 时,,
甲与乙刚好相距 公里时,即,
,解得:,
,解得:,
,解得:,
,解得:,
甲与乙刚好相距 公里的次数是 次,
故(4)正确;
11. D
【解析】由题意可知:当 在 上时,这时构不成三角形,此时 ,
当 在 上时, 的面积在增大, 与 重合时最大为 ,此时 ;
当 在 上时, 的面积不变等于 ,此时 ;
当 在 上时, 的面积在减小,此时 .
12.
13.
【解析】设 时,函数解析式为 ,
,,
解得 ,,
,
当 时,.
14. 或
【解析】当 时, 随 的增大而增大,
直线过点 ,,则 解得
一次函数的表达式为 ;
当 时, 随 的增大而减小,
直线过点 ,,
则
解得
一次函数的表达式为 .
故一次函数的表达式为 或 .
15. ①②④
【解析】①因为一次函数的图象是一条直线,由两点确定一条直线,故该函数可能是一次函数,故正确;
②由函数的定义:在一个变化过程中,有两个变量 ,,对于 的每一个取值, 都有唯一确定的值与之对应,则 是 的函数, 叫自变量,所以点 , 不可能同时在该函数图象上,故正确;
③因为函数关系不确定,所以函数值 不一定一直随自变量 的增大而减小,故错误;
④可能存在自变量 的某个取值范围,在这个范围内函数值 随自变量 增大而增大,故正确.
16.
【解析】 与 轴的交点坐标为 ,
由题知 ,
与 轴的交点为 ,
易知 ,
,
,
.
17. ,
【解析】: 与 轴和 轴分别交于点 和 ,,
: 与 轴和 轴分别交于点 ,,,
与 轴和 轴分别交于点 ,,,
与 轴和 轴分别交于点 ,,,
: 与 轴和 轴分别交于点 ,,.
18. (1) .
(2) .
19. (1)
(2)
(3)
(4)
20. 分两种情况:
①当 时,把 ,;, 分别代入一次函数的解析式 中,
得 解得
则这个函数的解析式是 .
②当 时,把 ,;, 分别代入一次函数的解析式 中,
得 解得
则这个函数的解析式是 .
故这个函数的解析式是 或 .
21. (1) 填表如下:
由题意,得 ;.
(2) 对于 ,
,
随 的增大而减小.
当 吨时, 最小,其最小值为 (元).
(3) 设两村的运费之和为 ,
则 .
,
随着 的增大而增大.
当 时, 有最小值, 最小值为 元.
按该方案调运,两村的运费之和最小,最小值为 元.
22. 解:由题意得,
解得,
∴ 直线 和直线 的交点坐标是
交点 落在平面直角坐标系的第四象限上.
23. (1) 当 ( 为整数)时,;
当 ( 为整数)时,;
当 ( 为整数)时,.
(2) 当 时,,
总价为 元,
方案一需付费 元.
方案二需付费 元.
当 时,;
当 时,;
当 时,.
答:当装修基金为 元时,两种方案均可;
当装修基金小于 元时,选择方案二;
当装修基金大于 元时,选择方案一.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
