2022-2023学年北师大版数学八年级下册6.2 平行四边形的判定 同步练习(word版 含解析)
文档属性
| 名称 | 2022-2023学年北师大版数学八年级下册6.2 平行四边形的判定 同步练习(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 515.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 13:52:23 | ||
图片预览


文档简介
北师大版八下 6.2 平行四边形的判定
一、选择题(共12小题)
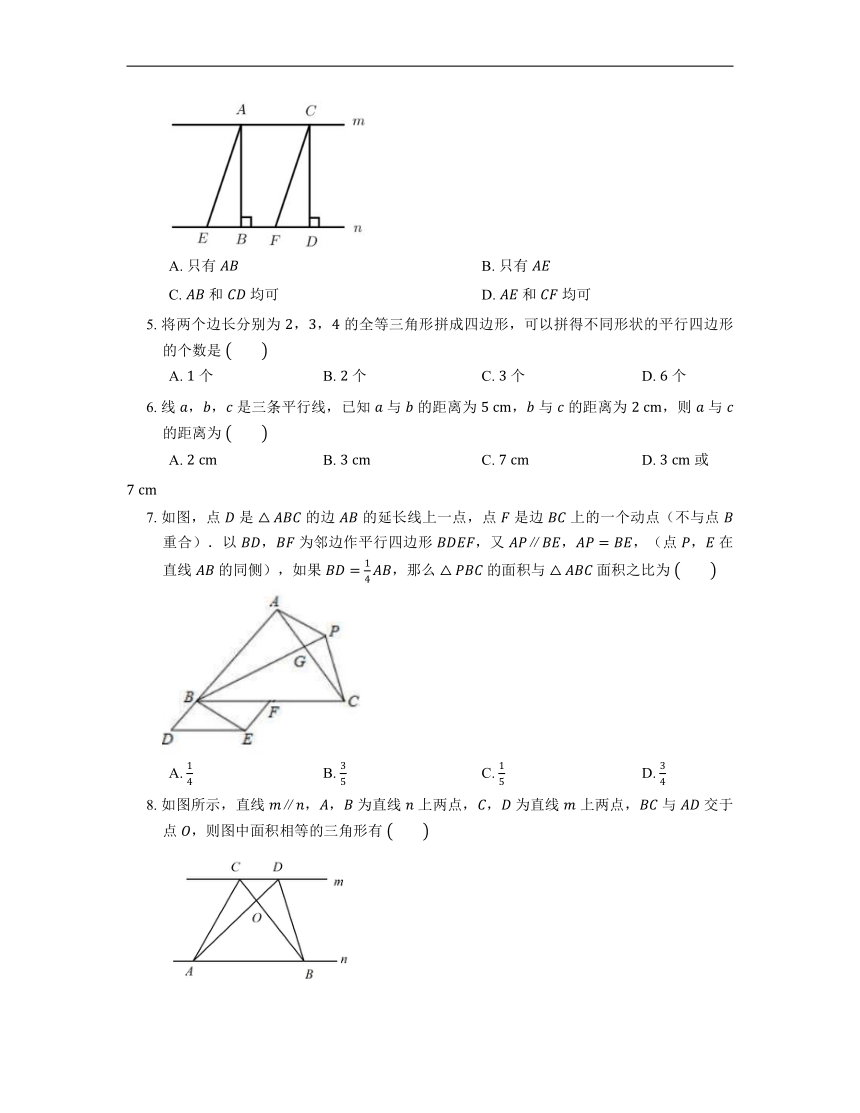
1. 根据图中所给的边长及角度,下列四边形中,为平行四边形的是
A. B.
C. D.
2. 如图,直线 , 是 上的动点,当点 的位置变化时,三角形 的面积将
A. 变大
B. 变小
C. 不变
D. 变大变小要看点 向左还是向右移动
3. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是
A. ①② B. ①④ C. ③④ D. ②③
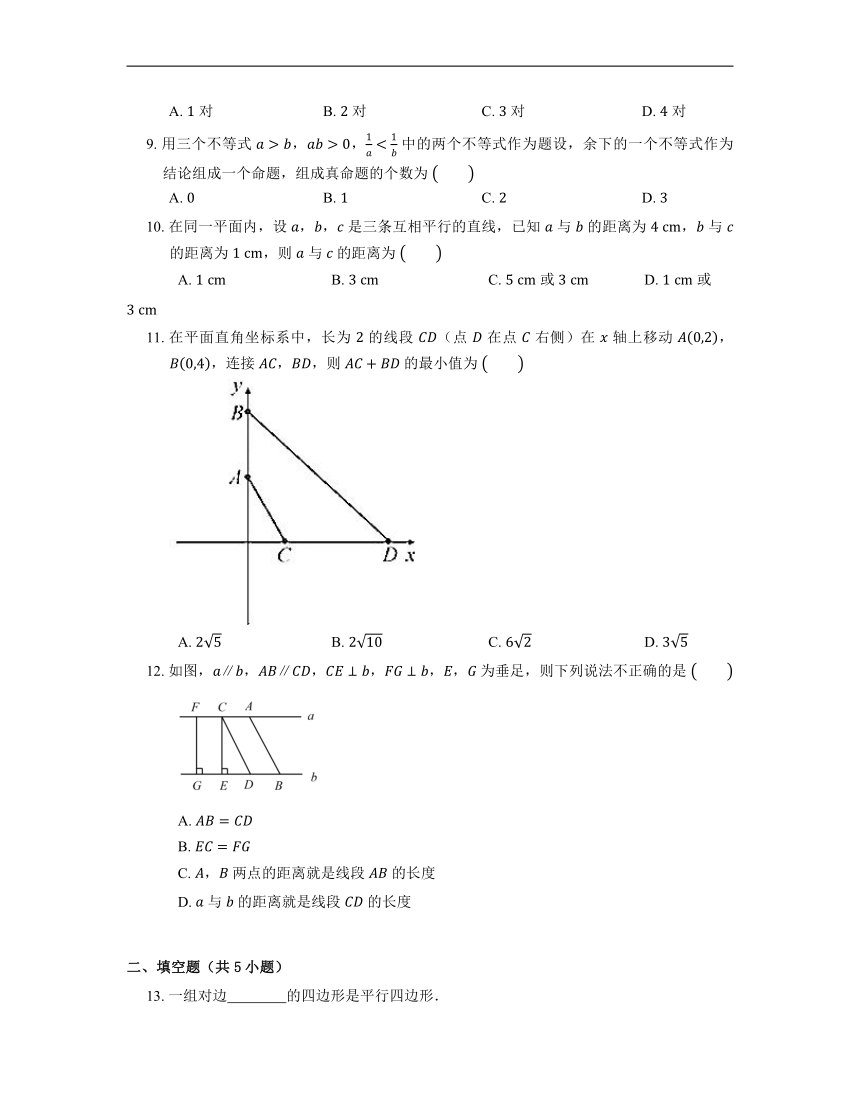
4. 已知直线 ,如图,下列哪条线段的长可以表示直线 与 之间的距离
A. 只有 B. 只有
C. 和 均可 D. 和 均可
5. 将两个边长分别为 ,, 的全等三角形拼成四边形,可以拼得不同形状的平行四边形的个数是
A. 个 B. 个 C. 个 D. 个
6. 线 ,, 是三条平行线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. D. 或
7. 如图,点 是 的边 的延长线上一点,点 是边 上的一个动点(不与点 重合).以 , 为邻边作平行四边形 ,又 ,,(点 , 在直线 的同侧),如果 ,那么 的面积与 面积之比为
A. B. C. D.
8. 如图所示,直线 ,, 为直线 上两点,, 为直线 上两点, 与 交于点 ,则图中面积相等的三角形有
A. 对 B. 对 C. 对 D. 对
9. 用三个不等式 ,, 中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为
A. B. C. D.
10. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
11. 在平面直角坐标系中,长为 的线段 (点 在点 右侧)在 轴上移动 ,,连接 ,,则 的最小值为
A. B. C. D.
12. 如图,,,,,, 为垂足,则下列说法不正确的是
A.
B.
C. , 两点的距离就是线段 的长度
D. 与 的距离就是线段 的长度
二、填空题(共5小题)
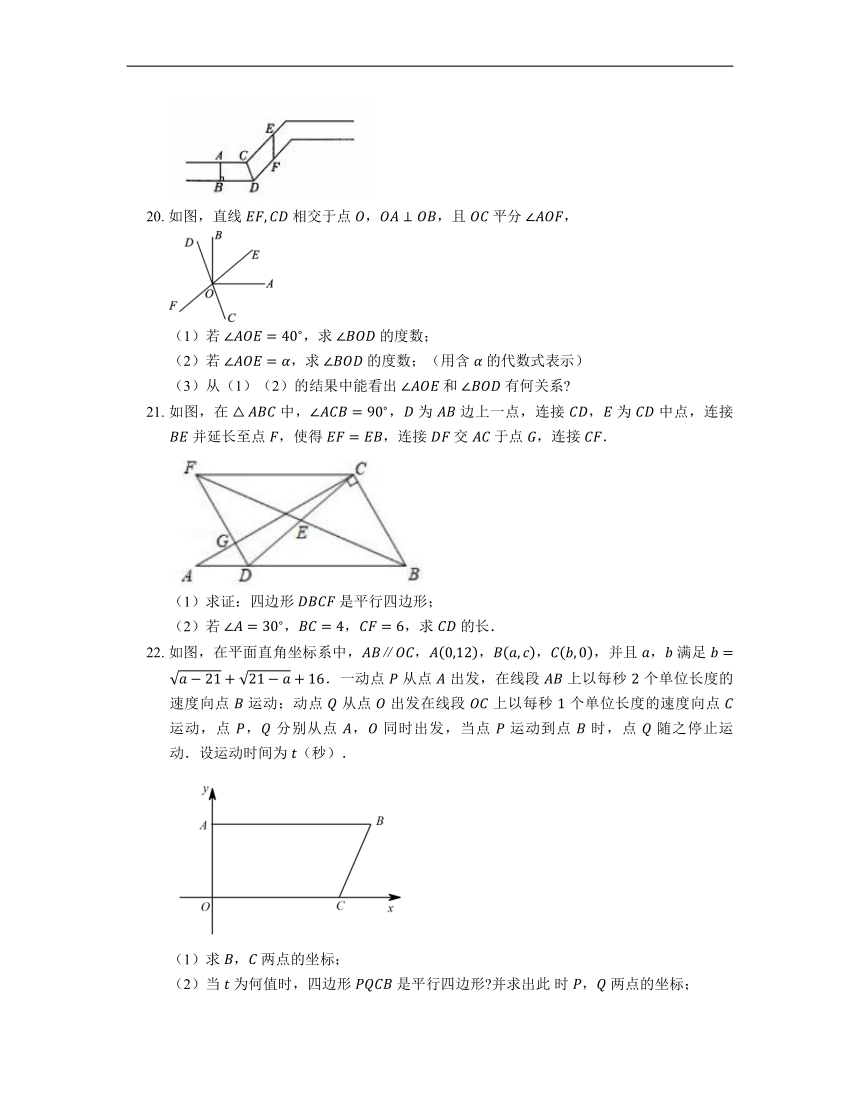
13. 一组对边 的四边形是平行四边形.
14. 如图,在四边形 中,若 ,则添加一个条件 ,能得到平行四边形 .(不添加辅助线,任意添加一个符合题意的条件即可)
15. 如图所示,,,四边形 的面积相等,并有 ,.由此可知, .
16. 如图所示,直线 ,点 在 上,若 ,, 的面积为 ,则 的面积为 .
17. 一个四边形四条边顺次是 ,,,,且 ,则这个四边形是 .
三、解答题(共5小题)
18. 已知:如图所示, 为线段 上一点,,,.求证:.
19. 一条公路的一段如图所示,图中哪条线段的长度能比较确切地描述这一段公路的宽度 请说明理由.
20. 如图,直线 相交于点 ,,且 平分 ,
(1)若 ,求 的度数;
(2)若 ,求 的度数;(用含 的代数式表示)
(3)从(1)(2)的结果中能看出 和 有何关系
21. 如图,在 中,, 为 边上一点,连接 , 为 中点,连接 并延长至点 ,使得 ,连接 交 于点 ,连接 .
(1)求证:四边形 是平行四边形;
(2)若 ,,,求 的长.
22. 如图,在平面直角坐标系中,,,,,并且 , 满足 .一动点 从点 出发,在线段 上以每秒 个单位长度的速度向点 运动;动点 从点 出发在线段 上以每秒 个单位长度的速度向点 运动,点 , 分别从点 , 同时出发,当点 运动到点 时,点 随之停止运动.设运动时间为 (秒).
(1)求 , 两点的坐标;
(2)当 为何值时,四边形 是平行四边形 并求出此 时 , 两点的坐标;
(3)当 为何值时, 是以 为腰的等腰三角形 并求出 , 两点的坐标.
答案
1. B
2. C
3. D
【解析】因为只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点,
所以带②③两块碎玻璃,就可以确定平行四边形的大小.
4. C
【解析】,
在同一平面内,垂直于 的线段,也垂直于 ,且该线段可表示 , 的最短距离.
故 , 可表示 , 的距离.
5. C
6. D
【解析】因为直线 的位置不明确,所以分①直线 在 , 外,②直线 在 , 之间两种情况讨论求解.
7. D
【解析】过点 作 交 于 ,连接 ,,
,.
四边形 是平行四边形,
,,
四边形 是平行四边形,
,,
即 ,
,, 共线,
设 ,
,
,
则 ,
,
,
,
四边形 是平行四边形,
,
,
.
8. C
9. D
【解析】命题①,如果 ,,那么 .
,.
整理得 .
命题①是真命题.
命题②,如果 ,,那么 .
,.
.
,,.
命题②是真命题.
命题③,如果 ,,那么 .
,.
,
,,.
命题③为真命题.综上,真命题的个数为 .
10. C
【解析】当直线 在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离 ;
当直线 不在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离 .
综上所述, 与 的距离为 或 .
11. B 【解析】作 关于 轴的对称点 ,
过 作 轴且 ,故 ,
连接 交 轴与 点,
过 作 交 轴于点 ,
所以四边形 为平行四边形,
此时 最短等于 的长,
即 .
12. D
13. 平行且相等
14. (答案不唯一)
15.
16.
17. 平行四边形
18. ,
,
在 和 中,
,
(全等三角形的对应角相等).
19. 线段 的长度能比较确切地描述这一段公路的宽度.线段 和 不与两平行线垂直,不是两条平行线间的距离.
20. (1) 因为 ,,
所以 .
又 平分 ,
所以 .
所以 .
(2) 因为 ,,
所以 .
又因为 平分 ,
所以 .
所以 .
(3) 从(1)(2)的结果中能看出 .
21. (1) 点 为 中点,
.
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,.
,.
在 中,,
,,
,
.
在 中,.
22. (1) 因为 ,
所以 ,,
故 ,.
(2) 根据题意得:,,
则:,,
因为当 时,四边形 是平行四边形,
所以 ,
计算得出:,
所以 ,.
(3) 当 时,过 作 ,如图所示,
根据题意得:,
计算得出:,
故 ,,
当 时,过 作 轴,如图所示,
根据题意得:,,
则 ,
计算得出:,,
故 ,.
一、选择题(共12小题)
1. 根据图中所给的边长及角度,下列四边形中,为平行四边形的是
A. B.
C. D.
2. 如图,直线 , 是 上的动点,当点 的位置变化时,三角形 的面积将
A. 变大
B. 变小
C. 不变
D. 变大变小要看点 向左还是向右移动
3. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是
A. ①② B. ①④ C. ③④ D. ②③
4. 已知直线 ,如图,下列哪条线段的长可以表示直线 与 之间的距离
A. 只有 B. 只有
C. 和 均可 D. 和 均可
5. 将两个边长分别为 ,, 的全等三角形拼成四边形,可以拼得不同形状的平行四边形的个数是
A. 个 B. 个 C. 个 D. 个
6. 线 ,, 是三条平行线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. D. 或
7. 如图,点 是 的边 的延长线上一点,点 是边 上的一个动点(不与点 重合).以 , 为邻边作平行四边形 ,又 ,,(点 , 在直线 的同侧),如果 ,那么 的面积与 面积之比为
A. B. C. D.
8. 如图所示,直线 ,, 为直线 上两点,, 为直线 上两点, 与 交于点 ,则图中面积相等的三角形有
A. 对 B. 对 C. 对 D. 对
9. 用三个不等式 ,, 中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为
A. B. C. D.
10. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
11. 在平面直角坐标系中,长为 的线段 (点 在点 右侧)在 轴上移动 ,,连接 ,,则 的最小值为
A. B. C. D.
12. 如图,,,,,, 为垂足,则下列说法不正确的是
A.
B.
C. , 两点的距离就是线段 的长度
D. 与 的距离就是线段 的长度
二、填空题(共5小题)
13. 一组对边 的四边形是平行四边形.
14. 如图,在四边形 中,若 ,则添加一个条件 ,能得到平行四边形 .(不添加辅助线,任意添加一个符合题意的条件即可)
15. 如图所示,,,四边形 的面积相等,并有 ,.由此可知, .
16. 如图所示,直线 ,点 在 上,若 ,, 的面积为 ,则 的面积为 .
17. 一个四边形四条边顺次是 ,,,,且 ,则这个四边形是 .
三、解答题(共5小题)
18. 已知:如图所示, 为线段 上一点,,,.求证:.
19. 一条公路的一段如图所示,图中哪条线段的长度能比较确切地描述这一段公路的宽度 请说明理由.
20. 如图,直线 相交于点 ,,且 平分 ,
(1)若 ,求 的度数;
(2)若 ,求 的度数;(用含 的代数式表示)
(3)从(1)(2)的结果中能看出 和 有何关系
21. 如图,在 中,, 为 边上一点,连接 , 为 中点,连接 并延长至点 ,使得 ,连接 交 于点 ,连接 .
(1)求证:四边形 是平行四边形;
(2)若 ,,,求 的长.
22. 如图,在平面直角坐标系中,,,,,并且 , 满足 .一动点 从点 出发,在线段 上以每秒 个单位长度的速度向点 运动;动点 从点 出发在线段 上以每秒 个单位长度的速度向点 运动,点 , 分别从点 , 同时出发,当点 运动到点 时,点 随之停止运动.设运动时间为 (秒).
(1)求 , 两点的坐标;
(2)当 为何值时,四边形 是平行四边形 并求出此 时 , 两点的坐标;
(3)当 为何值时, 是以 为腰的等腰三角形 并求出 , 两点的坐标.
答案
1. B
2. C
3. D
【解析】因为只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点,
所以带②③两块碎玻璃,就可以确定平行四边形的大小.
4. C
【解析】,
在同一平面内,垂直于 的线段,也垂直于 ,且该线段可表示 , 的最短距离.
故 , 可表示 , 的距离.
5. C
6. D
【解析】因为直线 的位置不明确,所以分①直线 在 , 外,②直线 在 , 之间两种情况讨论求解.
7. D
【解析】过点 作 交 于 ,连接 ,,
,.
四边形 是平行四边形,
,,
四边形 是平行四边形,
,,
即 ,
,, 共线,
设 ,
,
,
则 ,
,
,
,
四边形 是平行四边形,
,
,
.
8. C
9. D
【解析】命题①,如果 ,,那么 .
,.
整理得 .
命题①是真命题.
命题②,如果 ,,那么 .
,.
.
,,.
命题②是真命题.
命题③,如果 ,,那么 .
,.
,
,,.
命题③为真命题.综上,真命题的个数为 .
10. C
【解析】当直线 在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离 ;
当直线 不在 , 之间时,
因为 ,, 是三条互相平行的直线, 与 的距离为 , 与 的距离为 ,
所以 与 的距离 .
综上所述, 与 的距离为 或 .
11. B 【解析】作 关于 轴的对称点 ,
过 作 轴且 ,故 ,
连接 交 轴与 点,
过 作 交 轴于点 ,
所以四边形 为平行四边形,
此时 最短等于 的长,
即 .
12. D
13. 平行且相等
14. (答案不唯一)
15.
16.
17. 平行四边形
18. ,
,
在 和 中,
,
(全等三角形的对应角相等).
19. 线段 的长度能比较确切地描述这一段公路的宽度.线段 和 不与两平行线垂直,不是两条平行线间的距离.
20. (1) 因为 ,,
所以 .
又 平分 ,
所以 .
所以 .
(2) 因为 ,,
所以 .
又因为 平分 ,
所以 .
所以 .
(3) 从(1)(2)的结果中能看出 .
21. (1) 点 为 中点,
.
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,.
,.
在 中,,
,,
,
.
在 中,.
22. (1) 因为 ,
所以 ,,
故 ,.
(2) 根据题意得:,,
则:,,
因为当 时,四边形 是平行四边形,
所以 ,
计算得出:,
所以 ,.
(3) 当 时,过 作 ,如图所示,
根据题意得:,
计算得出:,
故 ,,
当 时,过 作 轴,如图所示,
根据题意得:,,
则 ,
计算得出:,,
故 ,.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
