2022-2023学年沪科版九年级数学上册22.2.3用边角的关系判定三角形相似 同步精练(word版 含答案)
文档属性
| 名称 | 2022-2023学年沪科版九年级数学上册22.2.3用边角的关系判定三角形相似 同步精练(word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 327.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 00:00:00 | ||
图片预览



文档简介
用边角的关系判定三角形相似
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,点D,E分别在△ABC的边AB,AC上,且DE与BC不平行.下列条件中,能判定△ADE与△ACB相似的是( )
A.= B.=
C.= D.=
2. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则必须具备的条件可以是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
3. 如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
A.∠DAC=∠ABC B.CA是∠BCD的平分线
C.AC2=BC·CD D.=
4. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.= B.=
C.= D.=
5. 如图,在等边三角形ABC中,点D,E分别在AC,AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
6. 如图,在△ABC中,点P在AB上,下列三个条件:①AP∶AC=AC∶AB;②AP∶BC=PC∶AB;③AB∶CP=AP∶CB.其中能判定△APC和△ACB相似的条件有( )
A.1个 B.2个 C.3个 D.0个
7. 如图,点A,B,C,D,E,F,G,H,K都是8×7的方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的( )
A.点F B.点G C.点H D.点K
8. 在图①、②所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开(裁剪办法已在图上标注),对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
A.只有①中的与△ABC相似
B.只有②中的与△ABC相似
C.都与△ABC相似
D.都与△ABC不相似
9. 如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长为( )
A. B.4 C. D.
10. 如图27-2-31,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长为( )
A. B. C. D.
二.填空题(共6小题,每小题4分,共24分)
11. 如图,在△ABC中,点D,E分别为边AB,AC上的点,试添加一个条件:_______________,使得△ADE与△ABC相似(任意写出一个满足条件的即可).
12. 如图,BC与AD相交于点O,OB∶OC=3∶1,OA=12 cm,OD=4 cm,AB=30 cm,则CD=________.
13. 在△ABC和△DEF中,∠A=40°,∠D=60°,∠E=80°,=,那么∠B的度数是________.
14. 如图,在等边三角形ABC中,D为AC的中点,=,则和△AED(不包含△AED)相似的三角形有_______个.
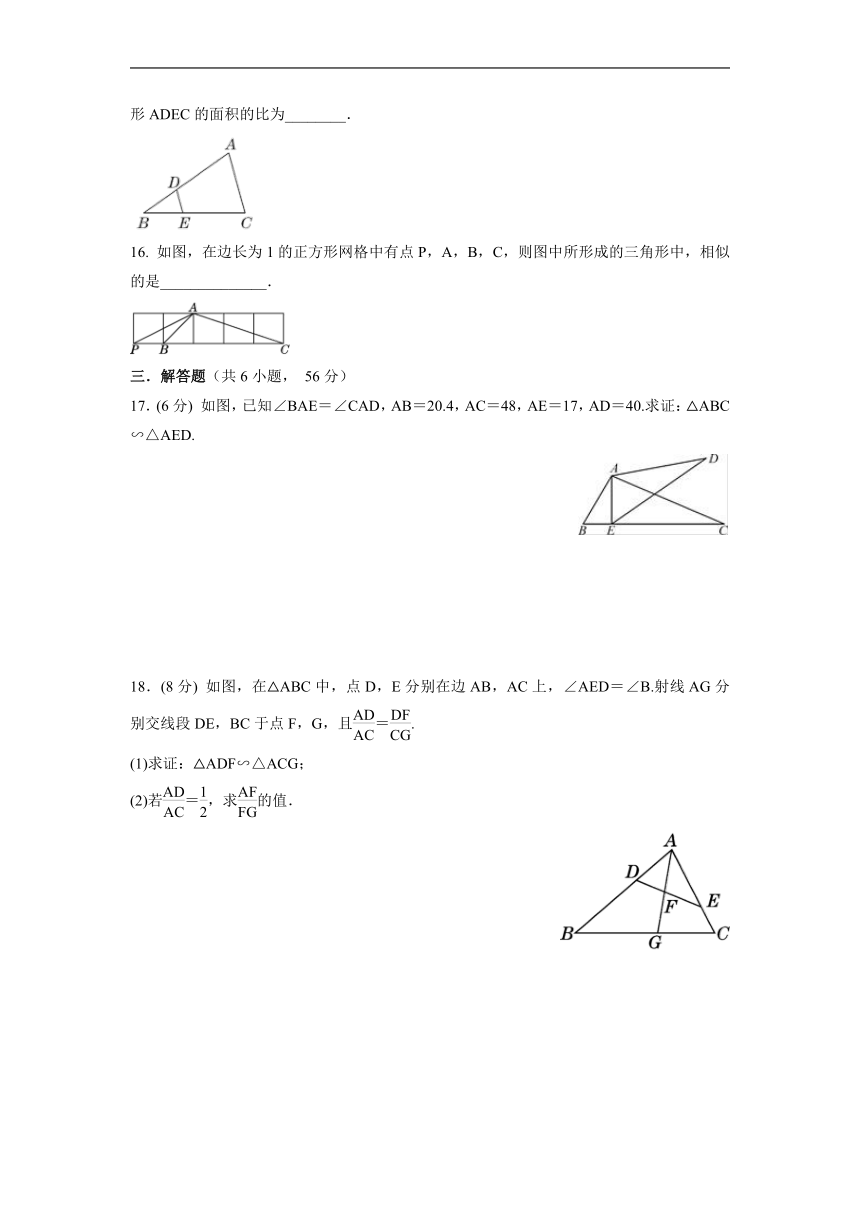
15. 如图,在△ABC中,点D,E分别在边BA,BC上,且==,则△DBE与四边形ADEC的面积的比为________.
16. 如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的是______________.
三.解答题(共6小题, 56分)
17.(6分) 如图,已知∠BAE=∠CAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
18.(8分) 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B.射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
19.(8分) 如图,在△ABC中,CD是边AB上的高,且CD2=AD·BD.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的度数.
20.(10分) 如图,在锐角△ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求的值.
21.(12分) 已知:如图,在△ABC中,点D,G分别在边AB,BC上,∠ACD=∠B,AG与CD相交于点F.
(1)求证:AC2=AD·AB;
(2)若=,求证:CG2=DF·BG.
22.(12分) 如图,在四边形ABCD中,AC平分∠DAB,AC2=AB·AD,∠ADC=90°,E为AB的中点.
(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求的值.
参考答案
1-5ADCCB 6-10ACBAA
11.=(答案不唯一)
12.10 cm
13.60°
14.3
15.
16.△APB∽△CPA
17. 证明:∵AB=20.4,AC=48,AE=17,AD=40,∴==1.2,==1.2,∴=.又∵∠BAE=∠CAD,∴∠BAC=∠EAD,∴△ABC∽△AED
18. 解:(1)∵∠AED=∠B,∠DAE=∠CAB,∴∠ADF=∠C. 又∵=,∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,∴=.又∵=,∴=.∴=1.
19. 解:(1)∵CD是边AB上的高,∴∠ADC=∠CDB=90°.又CD2=AD·BD,∴=,∴△ACD∽△CBD
(2)∵△ACD∽△CBD,∴∠A=∠BCD,在△ACD中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°
20. 解:(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°,∵∠EAF=∠GAC,∴∠AED=∠ACB,又∵∠EAD=∠CAB,∴△ADE∽△ABC
(2)由(1)可知,△ADE∽△ABC,∠AFE=∠AGC=90°,∴==,又∠EAF=∠GAC,∴△EAF∽△CAG,∴=,∴=
21. 证明:(1)∵∠ACD=∠B,∠CAD=∠BAC,∴△ACD∽△ABC.∴AC∶AB=AD∶AC.∴AC2=AD·AB.
(2)∵△ACD∽△ABC,∴∠ADF=∠ACG.又∵=,∴△ADF∽△ACG.∴∠DAF=∠CAF,即∠BAG=∠CAG.过点B作BE∥AC,交AG的延长线于点E,∴∠CAG=∠BEG,△ACG∽△EBG.∴=.又∵∠BAG=∠CAG,∴∠BAG=∠BEG.∴BA=BE.∴=.又∵=,=,∴=.∴CG2=DF·BG.
22. 解:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB.又∵AC2=AB·AD,∴AD∶AC=AC∶AB,∴△ADC∽△ACB
(2)CE∥AD,理由:∵△ADC∽△ACB,∴∠ACB=∠ADC=90°.又∵E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA.又∵∠DAC=∠CAE,∴∠DAC=∠ECA,∴CE∥AD
(3)∵AD=4,AB=6,CE=AB=AE=3,又∵CE∥AD,∴△CEF∽△ADF,∴==,∴=
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,点D,E分别在△ABC的边AB,AC上,且DE与BC不平行.下列条件中,能判定△ADE与△ACB相似的是( )
A.= B.=
C.= D.=
2. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则必须具备的条件可以是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
3. 如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
A.∠DAC=∠ABC B.CA是∠BCD的平分线
C.AC2=BC·CD D.=
4. 如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.= B.=
C.= D.=
5. 如图,在等边三角形ABC中,点D,E分别在AC,AB上,且AD∶AC=1∶3,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
6. 如图,在△ABC中,点P在AB上,下列三个条件:①AP∶AC=AC∶AB;②AP∶BC=PC∶AB;③AB∶CP=AP∶CB.其中能判定△APC和△ACB相似的条件有( )
A.1个 B.2个 C.3个 D.0个
7. 如图,点A,B,C,D,E,F,G,H,K都是8×7的方格纸中的格点,为使△DEM∽△ABC,则点M应是F,G,H,K四点中的( )
A.点F B.点G C.点H D.点K
8. 在图①、②所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开(裁剪办法已在图上标注),对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
A.只有①中的与△ABC相似
B.只有②中的与△ABC相似
C.都与△ABC相似
D.都与△ABC不相似
9. 如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长为( )
A. B.4 C. D.
10. 如图27-2-31,在△ABC中,AE交BC于点D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则DC的长为( )
A. B. C. D.
二.填空题(共6小题,每小题4分,共24分)
11. 如图,在△ABC中,点D,E分别为边AB,AC上的点,试添加一个条件:_______________,使得△ADE与△ABC相似(任意写出一个满足条件的即可).
12. 如图,BC与AD相交于点O,OB∶OC=3∶1,OA=12 cm,OD=4 cm,AB=30 cm,则CD=________.
13. 在△ABC和△DEF中,∠A=40°,∠D=60°,∠E=80°,=,那么∠B的度数是________.
14. 如图,在等边三角形ABC中,D为AC的中点,=,则和△AED(不包含△AED)相似的三角形有_______个.
15. 如图,在△ABC中,点D,E分别在边BA,BC上,且==,则△DBE与四边形ADEC的面积的比为________.
16. 如图,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的是______________.
三.解答题(共6小题, 56分)
17.(6分) 如图,已知∠BAE=∠CAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
18.(8分) 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B.射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
19.(8分) 如图,在△ABC中,CD是边AB上的高,且CD2=AD·BD.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的度数.
20.(10分) 如图,在锐角△ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求的值.
21.(12分) 已知:如图,在△ABC中,点D,G分别在边AB,BC上,∠ACD=∠B,AG与CD相交于点F.
(1)求证:AC2=AD·AB;
(2)若=,求证:CG2=DF·BG.
22.(12分) 如图,在四边形ABCD中,AC平分∠DAB,AC2=AB·AD,∠ADC=90°,E为AB的中点.
(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求的值.
参考答案
1-5ADCCB 6-10ACBAA
11.=(答案不唯一)
12.10 cm
13.60°
14.3
15.
16.△APB∽△CPA
17. 证明:∵AB=20.4,AC=48,AE=17,AD=40,∴==1.2,==1.2,∴=.又∵∠BAE=∠CAD,∴∠BAC=∠EAD,∴△ABC∽△AED
18. 解:(1)∵∠AED=∠B,∠DAE=∠CAB,∴∠ADF=∠C. 又∵=,∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,∴=.又∵=,∴=.∴=1.
19. 解:(1)∵CD是边AB上的高,∴∠ADC=∠CDB=90°.又CD2=AD·BD,∴=,∴△ACD∽△CBD
(2)∵△ACD∽△CBD,∴∠A=∠BCD,在△ACD中,∠ADC=90°,∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°
20. 解:(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°,∵∠EAF=∠GAC,∴∠AED=∠ACB,又∵∠EAD=∠CAB,∴△ADE∽△ABC
(2)由(1)可知,△ADE∽△ABC,∠AFE=∠AGC=90°,∴==,又∠EAF=∠GAC,∴△EAF∽△CAG,∴=,∴=
21. 证明:(1)∵∠ACD=∠B,∠CAD=∠BAC,∴△ACD∽△ABC.∴AC∶AB=AD∶AC.∴AC2=AD·AB.
(2)∵△ACD∽△ABC,∴∠ADF=∠ACG.又∵=,∴△ADF∽△ACG.∴∠DAF=∠CAF,即∠BAG=∠CAG.过点B作BE∥AC,交AG的延长线于点E,∴∠CAG=∠BEG,△ACG∽△EBG.∴=.又∵∠BAG=∠CAG,∴∠BAG=∠BEG.∴BA=BE.∴=.又∵=,=,∴=.∴CG2=DF·BG.
22. 解:(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB.又∵AC2=AB·AD,∴AD∶AC=AC∶AB,∴△ADC∽△ACB
(2)CE∥AD,理由:∵△ADC∽△ACB,∴∠ACB=∠ADC=90°.又∵E为AB的中点,∴CE=AB=AE,∴∠EAC=∠ECA.又∵∠DAC=∠CAE,∴∠DAC=∠ECA,∴CE∥AD
(3)∵AD=4,AB=6,CE=AB=AE=3,又∵CE∥AD,∴△CEF∽△ADF,∴==,∴=
