2022-2023学年北师大版八年级数学上册1.3 勾股定理的应用 同步练习 (word版 含解析)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册1.3 勾股定理的应用 同步练习 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 700.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:22:43 | ||
图片预览

文档简介
北师大版八上 1.3 勾股定理的应用
一、选择题
1. 如图,有一张直角三角形纸片,两直角边 ,,将 折叠,使点 与点 重合,折痕为 ,则 等于
A. B. C. D.
2. 如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为 ,在容器内壁离容器底部 的点 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿 的点 处,若蚂蚁吃到蜂蜜需爬行的最短路径为 ,则该圆柱底面周长为
A. B. C. D.
3. 小强量得家里新购置的彩电荧光屏的长为 ,宽为 ,则这台电视机的尺寸(屏幕的对角线长度为电视机的尺寸)最有可能是
A. 英寸 B. 英寸
C. 英寸 D. 英寸
4. 如图是一个四级台阶,它的每一级的长、宽、高分别为 ,,, 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
5. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多 ,当他把绳子下端拉开 后,发现下端刚好接触地面,则旗杆高度为
A. B. C. D.
6. 如图 所示,矩形纸片 中,,,现将其沿EF对折,使得点 与点 重合,则 的长为
A. B. C. D.
7. 2015年是国际“光”年,某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点 到顶点 镶有一圈金属丝,已知此三棱镜的高为 ,底面边长为 ,则这圈金属丝的长度至少为
A. B. C. D.
8. 迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会.小刘搬来一架高 米长的木梯架到墙上,木梯最顶端距地面高 米,则梯脚与墙角距离应为
A. 米 B. 米 C. 米 D. 米
9. 折叠长方形 的一边 ,使点 落在边 的点 处,若 ,,求 的长为
A. B. C. D.
10. 如图,小明(视为小黑点)站在一个高为 米的高台 上,利用旗杆 顶部的绳索,划过 到达与高台 水平距离为 米,高为 米的矮台 .那么小明在荡绳索的过程中离地面的最低点的高度 是
A. 米 B. 米 C. 米 D. 米
二、填空题
11. 如图,在 中,,,将 折叠,使得点 与 边的中点 重合,折痕为 ,则线段 的长为 .
12. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从点 开始经过 个侧面爬行一圈到达点 ,则蚂蚁爬行的最短路径长为 .
13. 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”(如图中的实线).其实他们仅仅少走了 ,却踩伤了花草.
14. 如图,圆柱形容器高 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的 处,则蚂蚁从外壁 处到达内壁 处的最短距离为 .
15. 如图,在矩形 中,,,点 在线段 上运动,现将纸片折叠,使点 与点 重合,得折痕 (点 、 为折痕与矩形边的交点),设 ,当点 落在线段 上,点 落在线段 上时, 的取值范围是 .
16. 如图,在离水面高度为 米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为 米,此人以 米每秒的速度收绳, 秒后船移动到点 的位置,问船向岸边移动 米.(假设绳子是直的)
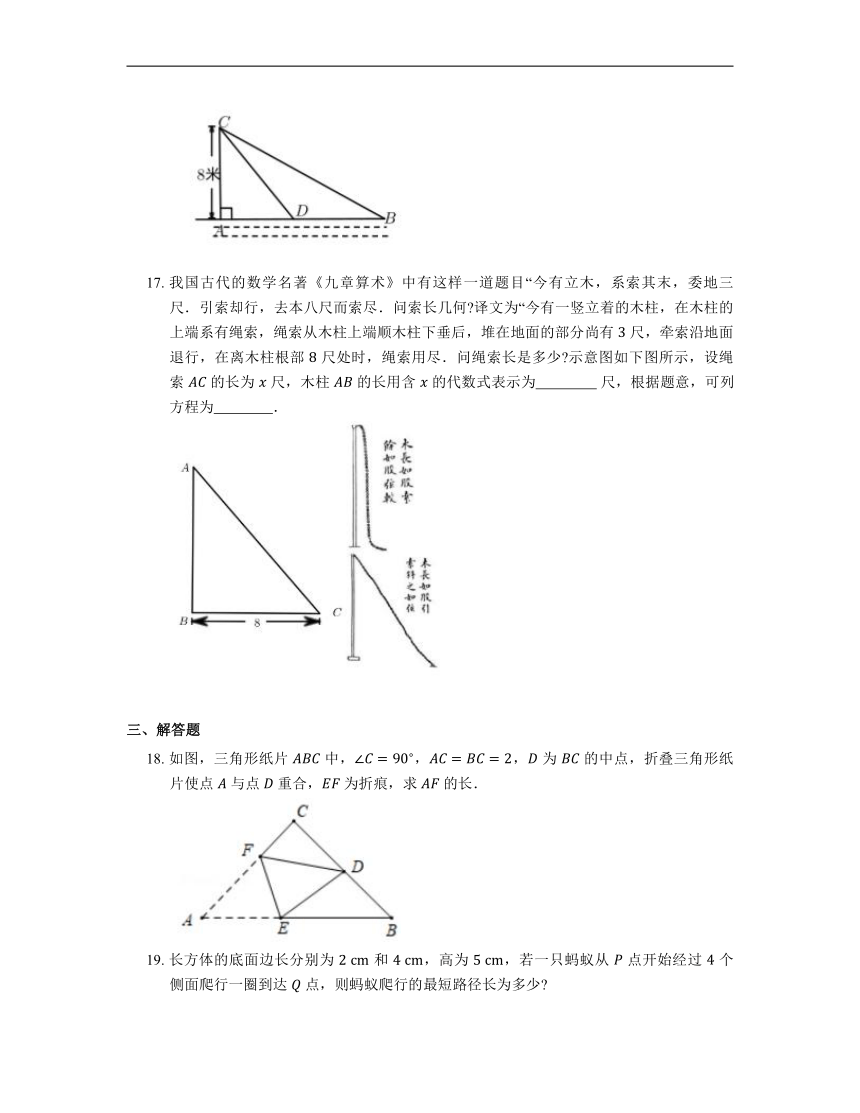
17. 我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何 译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有 尺,牵索沿地面退行,在离木柱根部 尺处时,绳索用尽.问绳索长是多少 示意图如下图所示,设绳索 的长为 尺,木柱 的长用含 的代数式表示为 尺,根据题意,可列方程为 .
三、解答题
18. 如图,三角形纸片 中,,, 为 的中点,折叠三角形纸片使点 与点 重合, 为折痕,求 的长.
19. 长方体的底面边长分别为 和 ,高为 ,若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为多少
20. 如图,某地方政府决定在相距 的 , 两站之间的公路旁 点修建一个土特产加工基地,且使 , 两村到 点的距离相等,已知 于 , 于 ,,,那么基地 应建在离 站多少千米的地方
21. 如图,在四边形 中,,,.将四边形 沿直线 折叠,使点 落在 边上的点 处.
(1)求 的长.
(2)求 的长.
22. 下面的两个图形通过折叠,能围成什么几何体
23. 某公司举行开业一周年庆典,准备在一个长 ,高 的台阶上铺设地毯(如图所示),已知台阶的宽为 .
(1)请你算一算共需购买多大面积的地毯;
(2)若地毯的价格为 ,则购买地毯需花费多少元
24. 如图,将长方形纸片 的一边 向下折叠,点 落在 边上的点 处.已知 ,,求 的长.
答案
1. C
2. D
3. C
4. C
5. C
6. B
【解析】设 ,则 .
矩形纸片 中,,,现将其沿 对折,使得点 与点 重合,
.
在 中,
,
.
解得 .
7. B
8. A
9. A 【解析】设 的长为 ,
.
折叠后的图形是 ,
,,.
,
.
又 ,
在 中,
根据勾股定理,得 ,
,
.
.
在 中,根据勾股定理,得:,
,,
即 ,
化简,得 .
.
故 的长为 .
10. A
【解析】作 于 , 于 ,如图所示:
则 ,
因为 ,
所以 .
在 和 中,
所以 ,
所以 ,,
所以 (米),
因为 (米),
因为 米,
所以 (米),
所以 米, 米,
所以 (米),
(米),
由勾股定理得:(米),
所以 (米).
11.
【解析】, 是 的中点,
,
由折叠知 ,
设 ,则 ,
在 中,,
,
解得:,
即 .
12.
13.
14.
15.
【解析】①当 、 重合时, 的值最小;
根据折叠的性质知:;
在 中,,,由勾股定理的,得 .
②当 、 重合时, 的值最大;
由折叠的性质可得 ,即 的最大值为 .
16.
【解析】在 中:
, 米, 米,
(米),
此人以 米每秒的速度收绳, 秒后船移动到点 的位置,
(米),
(米),
(米),
答:船向岸边移动了 米.
17. ,
【解析】;
由题意可知 ,
由勾股定理可得 .
18. , 为 的中点,
,
由折叠的性质得:,
,
,
在 中,由勾股定理得:,
即 ,
解得:.
19. 该长方体的侧面展开图为
,,
即蚂蚁爬行的最短路径长为 .
20. 设基地 应建在离 站 的地方,
则 .
在 中,根据勾股定理得 ,
.
在 中,根据勾股定理得 ,
.
又 两村到 点的距离相等,
,
,
,解得 ,
基地 应建在离 站 的地方.
21. (1) 是 折叠得到的,
,
在 中,
.
(2) 是 折叠得到的,
.
设 ,则 ,
在 中,,,
,即 ,
解得:,
的长度为 .
22. 长方体盒子.
23. (1) 依题意,图中直角三角形一直角边长为 米,斜边长为 米,
根据勾股定理另一直角边长为 (米),
则需购买红地毯的长为 (米),
红地毯的宽则是台阶的宽,为 米,
所以面积是 (平方米).
(2) (元),
答:则购买地毯需花费 元.
24. 根据题意,得 ,
,,
.
在 中,根据勾股定理,
得 ,
.
设 ,则 .
在 中,根据勾股定理,
得 ,
即 .
解这个方程,得 ,
即 的长为 .
一、选择题
1. 如图,有一张直角三角形纸片,两直角边 ,,将 折叠,使点 与点 重合,折痕为 ,则 等于
A. B. C. D.
2. 如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为 ,在容器内壁离容器底部 的点 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿 的点 处,若蚂蚁吃到蜂蜜需爬行的最短路径为 ,则该圆柱底面周长为
A. B. C. D.
3. 小强量得家里新购置的彩电荧光屏的长为 ,宽为 ,则这台电视机的尺寸(屏幕的对角线长度为电视机的尺寸)最有可能是
A. 英寸 B. 英寸
C. 英寸 D. 英寸
4. 如图是一个四级台阶,它的每一级的长、宽、高分别为 ,,, 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
5. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多 ,当他把绳子下端拉开 后,发现下端刚好接触地面,则旗杆高度为
A. B. C. D.
6. 如图 所示,矩形纸片 中,,,现将其沿EF对折,使得点 与点 重合,则 的长为
A. B. C. D.
7. 2015年是国际“光”年,某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点 到顶点 镶有一圈金属丝,已知此三棱镜的高为 ,底面边长为 ,则这圈金属丝的长度至少为
A. B. C. D.
8. 迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会.小刘搬来一架高 米长的木梯架到墙上,木梯最顶端距地面高 米,则梯脚与墙角距离应为
A. 米 B. 米 C. 米 D. 米
9. 折叠长方形 的一边 ,使点 落在边 的点 处,若 ,,求 的长为
A. B. C. D.
10. 如图,小明(视为小黑点)站在一个高为 米的高台 上,利用旗杆 顶部的绳索,划过 到达与高台 水平距离为 米,高为 米的矮台 .那么小明在荡绳索的过程中离地面的最低点的高度 是
A. 米 B. 米 C. 米 D. 米
二、填空题
11. 如图,在 中,,,将 折叠,使得点 与 边的中点 重合,折痕为 ,则线段 的长为 .
12. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从点 开始经过 个侧面爬行一圈到达点 ,则蚂蚁爬行的最短路径长为 .
13. 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”(如图中的实线).其实他们仅仅少走了 ,却踩伤了花草.
14. 如图,圆柱形容器高 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时已知蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的 处,则蚂蚁从外壁 处到达内壁 处的最短距离为 .
15. 如图,在矩形 中,,,点 在线段 上运动,现将纸片折叠,使点 与点 重合,得折痕 (点 、 为折痕与矩形边的交点),设 ,当点 落在线段 上,点 落在线段 上时, 的取值范围是 .
16. 如图,在离水面高度为 米的岸上,有人用绳子拉船靠岸,开始时绳子 的长为 米,此人以 米每秒的速度收绳, 秒后船移动到点 的位置,问船向岸边移动 米.(假设绳子是直的)
17. 我国古代的数学名著《九章算术》中有这样一道题目“今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何 译文为“今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有 尺,牵索沿地面退行,在离木柱根部 尺处时,绳索用尽.问绳索长是多少 示意图如下图所示,设绳索 的长为 尺,木柱 的长用含 的代数式表示为 尺,根据题意,可列方程为 .
三、解答题
18. 如图,三角形纸片 中,,, 为 的中点,折叠三角形纸片使点 与点 重合, 为折痕,求 的长.
19. 长方体的底面边长分别为 和 ,高为 ,若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为多少
20. 如图,某地方政府决定在相距 的 , 两站之间的公路旁 点修建一个土特产加工基地,且使 , 两村到 点的距离相等,已知 于 , 于 ,,,那么基地 应建在离 站多少千米的地方
21. 如图,在四边形 中,,,.将四边形 沿直线 折叠,使点 落在 边上的点 处.
(1)求 的长.
(2)求 的长.
22. 下面的两个图形通过折叠,能围成什么几何体
23. 某公司举行开业一周年庆典,准备在一个长 ,高 的台阶上铺设地毯(如图所示),已知台阶的宽为 .
(1)请你算一算共需购买多大面积的地毯;
(2)若地毯的价格为 ,则购买地毯需花费多少元
24. 如图,将长方形纸片 的一边 向下折叠,点 落在 边上的点 处.已知 ,,求 的长.
答案
1. C
2. D
3. C
4. C
5. C
6. B
【解析】设 ,则 .
矩形纸片 中,,,现将其沿 对折,使得点 与点 重合,
.
在 中,
,
.
解得 .
7. B
8. A
9. A 【解析】设 的长为 ,
.
折叠后的图形是 ,
,,.
,
.
又 ,
在 中,
根据勾股定理,得 ,
,
.
.
在 中,根据勾股定理,得:,
,,
即 ,
化简,得 .
.
故 的长为 .
10. A
【解析】作 于 , 于 ,如图所示:
则 ,
因为 ,
所以 .
在 和 中,
所以 ,
所以 ,,
所以 (米),
因为 (米),
因为 米,
所以 (米),
所以 米, 米,
所以 (米),
(米),
由勾股定理得:(米),
所以 (米).
11.
【解析】, 是 的中点,
,
由折叠知 ,
设 ,则 ,
在 中,,
,
解得:,
即 .
12.
13.
14.
15.
【解析】①当 、 重合时, 的值最小;
根据折叠的性质知:;
在 中,,,由勾股定理的,得 .
②当 、 重合时, 的值最大;
由折叠的性质可得 ,即 的最大值为 .
16.
【解析】在 中:
, 米, 米,
(米),
此人以 米每秒的速度收绳, 秒后船移动到点 的位置,
(米),
(米),
(米),
答:船向岸边移动了 米.
17. ,
【解析】;
由题意可知 ,
由勾股定理可得 .
18. , 为 的中点,
,
由折叠的性质得:,
,
,
在 中,由勾股定理得:,
即 ,
解得:.
19. 该长方体的侧面展开图为
,,
即蚂蚁爬行的最短路径长为 .
20. 设基地 应建在离 站 的地方,
则 .
在 中,根据勾股定理得 ,
.
在 中,根据勾股定理得 ,
.
又 两村到 点的距离相等,
,
,
,解得 ,
基地 应建在离 站 的地方.
21. (1) 是 折叠得到的,
,
在 中,
.
(2) 是 折叠得到的,
.
设 ,则 ,
在 中,,,
,即 ,
解得:,
的长度为 .
22. 长方体盒子.
23. (1) 依题意,图中直角三角形一直角边长为 米,斜边长为 米,
根据勾股定理另一直角边长为 (米),
则需购买红地毯的长为 (米),
红地毯的宽则是台阶的宽,为 米,
所以面积是 (平方米).
(2) (元),
答:则购买地毯需花费 元.
24. 根据题意,得 ,
,,
.
在 中,根据勾股定理,
得 ,
.
设 ,则 .
在 中,根据勾股定理,
得 ,
即 .
解这个方程,得 ,
即 的长为 .
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
