2.3图形的位似(1)

课件17张PPT。§2.图形的位似(1)九年级数学(上)第二章：图形与变换认真阅读课本第64、65页，回答以下问题：1、什么叫相似图形？2、什么叫位似图形？位似中心？位似比？3、位似图形有什么性质？4、如何作位似图形？本节教学目标1.理解位似图形的概念，知道利用位似可以将一个图形放大或缩小。
2.会判定两个图形是否是位似图形。
3.掌握位似图形的性质，回作出与已知简单图形位似的图形。 前面我们已经学习了图形的哪些变换？平移
旋转（包括中心对称）
轴对称以上几种图形的变换：
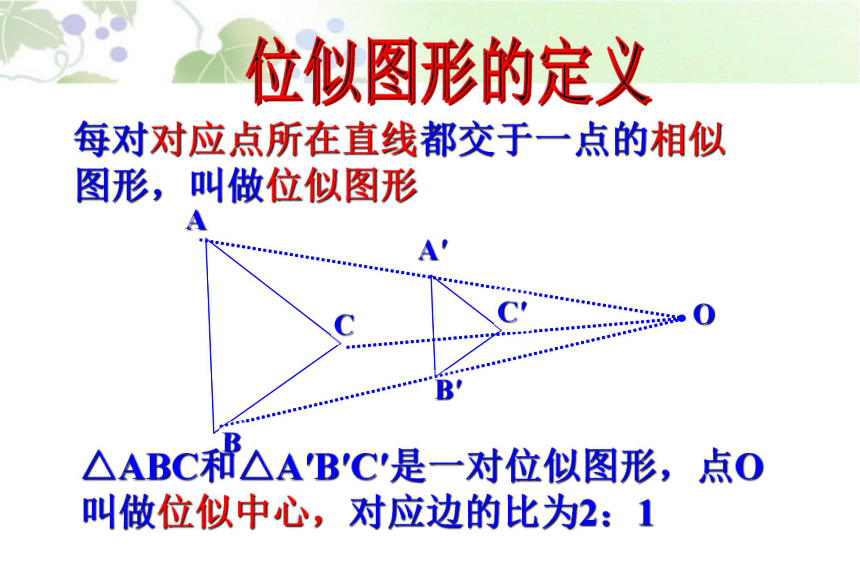
只改变图形的位置，不改变图形的形状和大小。下面请欣赏如下图形的变换位似图形的定义每对对应点所在直线都交于一点的相似图形，叫做位似图形ABCA′B′C′O△ABC和△A′B′C′是一对位似图形，点O叫做位似中心，对应边的比为2：1思考：是否相似图形一定是位似图形？
ABCDA′B′C′D′O 位似中心是：O对应边的比：AB：A′B′位似中心是：点OO对应边的比：AB：A′B′A B C D A′ B′ C′ D′ A B C D (A′) B′ C′ D′ 位似中心是：点A 位似图形的性质：如果两个多边形是位似图形，且对应边平行或在同一直线上，那么图形上任意一对对应点到位似中心的距离之比都等于对应边的比。C′B′A′A′B′C′通过上例，我们知道：利用位似，我们可以将一个图形放大或缩小。O.ABCA'C’B’.　　如图，已知△ABC和点O.以O为位似中心，求作△ABC的位似图形，并把△ABC的边长扩大到原来的两倍. OA:OA’ =OB:OB’ =OC:OC’= 1:2利用位似可以将一个图形放大或缩小思考：还有没其他作法？O.ABA'C’B’C思考：位似中心还可以在哪呢？回味无穷位似图形的概念：
相似图形 每对对应顶点所在直线交于一点
位似图形的性质：
1.对应边平行或在同一直线上。
2.位似图形上的任意一对对应点到位似中心的距离之比等于位似比。
应用：利用位似将一个图形放大或缩小
注意：位似中心可以在两个位似图形的内部，外部也可以在边上或公共顶点处。
其中，每种情况又分为对应点在位似中心 的同侧和异测两种类型。
O 互动 57页
1. 2