1.1探索勾股定理（1）[上学期]

1.1 探索勾股定理(1)
教学目标 知识与技能目标:掌握勾股定理;了解利用拼图验证勾股定理的方法;能运用勾股定理解决一些实际问题.过程与方法目标:经历探索勾股定理及验证勾股定理的过程;鼓励用多种方法验证勾股定理.情感与态度目标:学会用勾股定理解决实际问题,体会数学的应用价值;提倡多渠道查阅有关勾股定理的资料,体现数学的文化价值.
教学难点 利用拼图验证勾股定理的方法; 能运用勾股定理解决一些实际问题.
知识重点 掌握勾股定理;了解利用拼图验证勾股定理的方法; 运用勾股定理解决一些实际问题.
教学用具 课件, 四个直角三角形纸片.
第一课时教学过程 师生活动 自我
引入 师：勾股定理有着悠久的历史。古巴比伦人和古代中国人看出了这个关系；古希腊的毕达哥拉斯学派首先证明了这个关系。很多具有古老文化的民族和国家都会说：我们首先认识的数学定理是勾股定理。正因为如此，当科学家们想要弄清楚其他星球上是否存在着“人”并试图与“他们”取得联系时，数学家们就曾提出建议用勾股定理的图案来作为与“外星人”联系的信号（提出此建议者是我国的数学家华罗庚）。那么勾股定理到底是怎样的呢？下面，我们就来探索一下。[板书] 1.1探索勾股定理
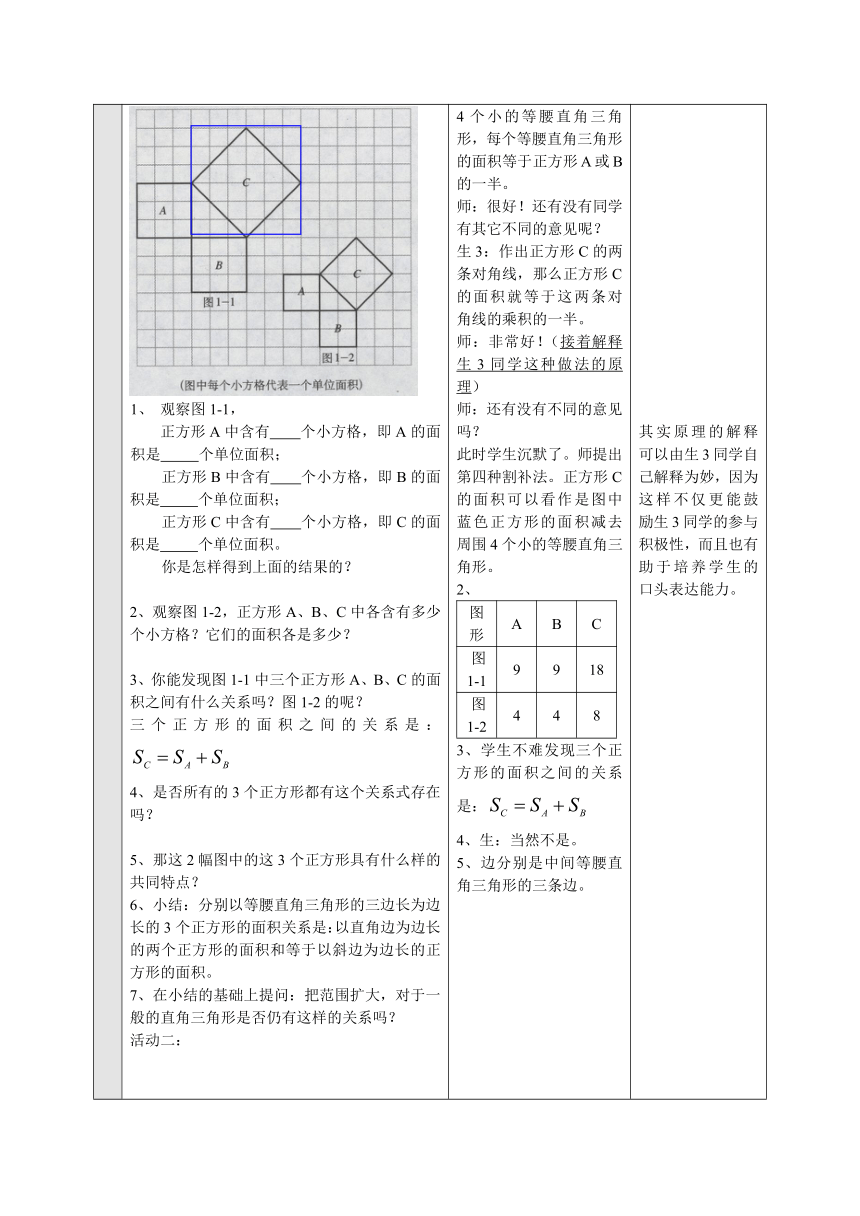
概念分析 活动一：探索以等腰直角三角形（要由学生自己观察得出）的三边为边长的3个正方形的面积关系？观察图1-1，正方形A中含有 个小方格，即A的面积是 个单位面积；正方形B中含有 个小方格，即B的面积是 个单位面积；正方形C中含有 个小方格，即C的面积是 个单位面积。你是怎样得到上面的结果的？2、观察图1-2，正方形A、B、C中各含有多少个小方格？它们的面积各是多少？3、你能发现图1-1中三个正方形A、B、C的面积之间有什么关系吗？图1-2的呢？三个正方形的面积之间的关系是：4、是否所有的3个正方形都有这个关系式存在吗？5、那这2幅图中的这3个正方形具有什么样的共同特点？6、小结：分别以等腰直角三角形的三边长为边长的3个正方形的面积关系是：以直角边为边长的两个正方形的面积和等于以斜边为边长的正方形的面积。7、在小结的基础上提问：把范围扩大，对于一般的直角三角形是否仍有这样的关系吗？活动二：1、观察图1-3，图1-4，并填写下表：图形ABC图1-316925图1-44913你是怎样得到上面的结果的？2、三个正方形A、B、C的面积之间有什么关系？3、小结：分别以直角三角形的三边为边长的3个正方形的面积之间有如下关系——以直角边为边长的两个正方形的面积和等于以斜边为边长的正方形的面积。活动三：议一议你能用三角形的边长表示正方形的面积吗？你能发现直角三角形的三边长度之间存在什么关系吗？请用文字语言描述一下这条等式：直角三角形两直角边的平方和等于斜边的平方。请分别以5cm，12cm为直角边作出一个直角三角形，并测量斜边的长度。然后，验证是否对这个三角形成立。归纳勾股定理如果直角三角形两直角边分别为a、b，斜边为c，那么。即直角三角形两直角边的平方和等于斜边的平方。名词解释“勾股定理”：我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦。提出问题：锐角三角形和钝角三角形的三边长是否满足？小结：勾股定理反映的是直角三角形的三边关系。 9，9；9，9；18，18学生交流：数出来的。师：正方形A、B好数，那么正方形C，你们是怎么数出来的呢？生1：旁边两个小的直角三角形的面积之和等于一个正方形的面积。师：有没有不同意见呢？生2：把正方形C分割成4个小的等腰直角三角形，每个等腰直角三角形的面积等于正方形A或B的一半。师：很好！还有没有同学有其它不同的意见呢？生3：作出正方形C的两条对角线，那么正方形C的面积就等于这两条对角线的乘积的一半。师：非常好！（接着解释生3同学这种做法的原理）师：还有没有不同的意见吗？此时学生沉默了。师提出第四种割补法。正方形C的面积可以看作是图中蓝色正方形的面积减去周围4个小的等腰直角三角形。2、图形ABC图1-19918图1-24483、学生不难发现三个正方形的面积之间的关系是：4、生：当然不是。5、边分别是中间等腰直角三角形的三条边。1、思路同活动一。2、学生想不到用字母表示直角三角形的边长。经过教师提示才明白。，，学生在这一环做得不好，他们不懂得验证的意思——作出这个直角三角形后，不测量斜边的长度，而是通过计算出斜边的长度。当我要求他们测量一下看看结果是否跟计算所得数据一致时，他们马上说一致的，由勾股定理可得。6、通过数格子发现对锐角三角形有，而对钝角三角形则有 其实原理的解释可以由生3同学自己解释为妙，因为这样不仅更能鼓励生3同学的参与积极性，而且也有助于培养学生的口头表达能力。这里，教师的提示太露骨，不够自然。可以表述为：对，当直角三角形的边长已知时，我们就可以分别求出这三个正方形的面积。可是，直角三角形很多很多个，那每个直角三角形都要测量不就不太可能了呢？有没有办法用一条式子表示一般情况呢？对此，我只能告诉他们不能用本身来证明自己是对的，就像不能用小偷的话来说明小偷是无辜的一样。
课堂练习 P6——1、2、3、4要求记忆11至19的平方结果。P5——读一读
小结与作业
课堂小结 本堂课你学习了什么？有哪些收获和体会？分别以直角三角形的三边为边长的3个正方形的面积之间有如下关系——以直角边为边长的两个正方形的面积和等于以斜边为边长的正方形的面积。勾股定理：如果直角三角形两直角边分别为a、b，斜边为c，那么。即直角三角形两直角边的平方和等于斜边的平方。
本课作业 数学作业本查阅书籍、上网寻找相关勾股定理的资料，并制成一份小报。这个任务可以独立完成，也可以和几个同学合作。2周后交。做4个全等的直角三角形纸片，明天上课用。
本课教育评注（课堂设计理念，实际教学效果及改进设想）
本课设计思路根据的是新课程改革中所倡导的探究学习过程而设计的。在实际教学过程中，学生的参与积极性也是挺高的，对勾股定理的掌握也不错。但此课的教学过程，也充分暴露出教师对课堂教学新理念的掌握还很不够——在启发学生时，有时语言不够自然，有时还会越俎代庖，没能充分发挥学生的主体地位。另外，部分学生的逻辑思维比较混乱，教师需要在平时对其多加引导和锻炼。还有，大部分学生的预习不仅没能帮助他们更好地学习新课，反而还阻碍了他们对新知识的探究过程。这是今后要注意引导的地方。
勾
股
弦