2022-2023学年高中数学选择性必修2教学课件 3.2.1.1直线的倾斜角与斜率(共34张PPT)
文档属性
| 名称 | 2022-2023学年高中数学选择性必修2教学课件 3.2.1.1直线的倾斜角与斜率(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 11:05:58 | ||
图片预览





文档简介
(共34张PPT)
2022-2023学年高中数学选择性必修2教学课件
知识回顾:
我们学过:y=x+1,它表示什么?
如何在平面直角坐标系内确定它的位置
y
1
x
o
-1
对于平面直角坐标系内的一条直线 l ,它的位置由哪些条件确定?
x
y
O
l
问题引入
我们知道,两点确定一条直线.一点能确定一条直线的位置吗?已知直线 l 经过点P,直线 l 的位置能够确定吗?
问题引入
x
y
O
l
l’
l’’
P
过一点P可以作无数条直线l 1, l 2 , l 3 ,…它们都经过点P (组成一个直线束),这些直线区别在哪里呢?
问题引入
x
y
O
l
l’
l’’
P
容易看出,它们的倾斜程度不同.怎样描述直线的倾斜程度呢?
问题引入
x
y
O
l
l’
l’’
P
x
y
o
l
α
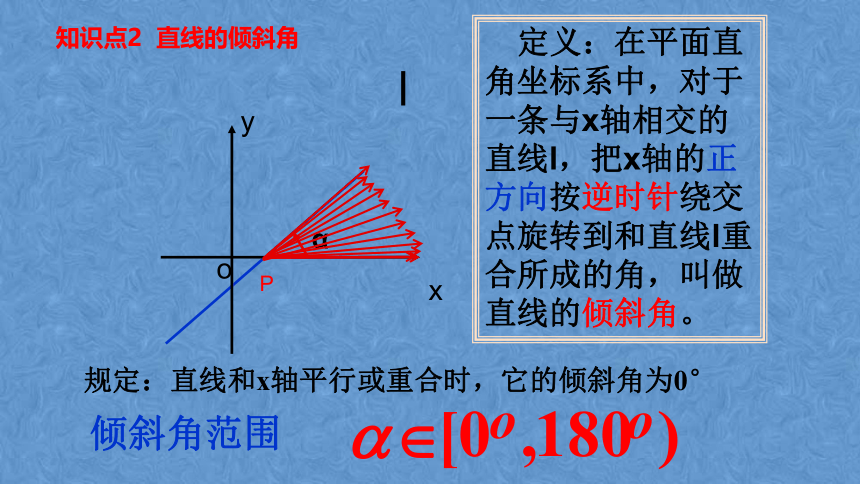
定义:在平面直角坐标系中,对于一条与x轴相交的直线l,把x轴的正方向按逆时针绕交点旋转到和直线l重合所成的角,叫做直线的倾斜角。
规定:直线和x轴平行或重合时,它的倾斜角为0°
)
180
,
0
[
o
o
a
倾斜角范围
P
知识点2 直线的倾斜角
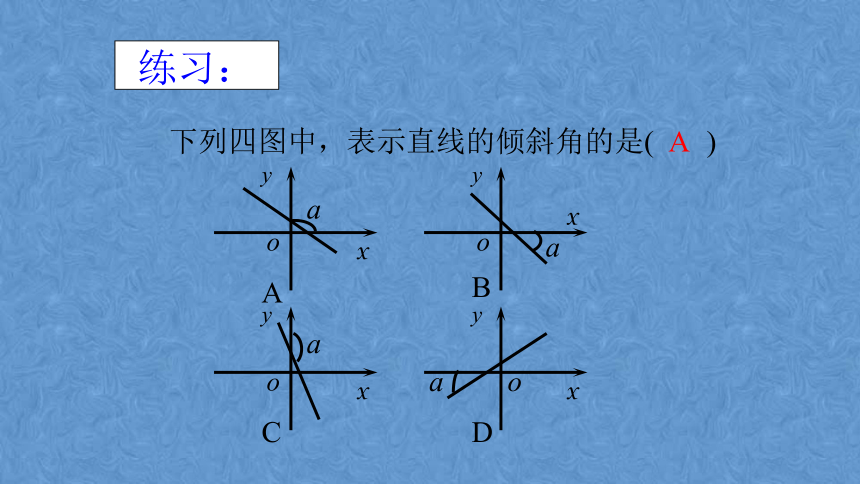
下列四图中,表示直线的倾斜角的是( )
练习:
A
B
C
D
A
特别地,当直线和x轴平行或重合时,
它的倾斜角为0°。
直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。
坐标平面上任何一条直都有唯一的倾斜角。
倾斜角的取值范围是:
)
180
,
0
[
o
o
a
思考: 日常生活中,还有没有刻画倾斜程度的量?
如图,日常生活中,我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即
升高量
前进量
A
B
C
D
可理解为:在水平方向移动1km,在铅直方向上升或下降的数值(km),这个比值表示了坡度的大小。刻画了道路等的倾斜程度。
知识点2 斜率
【探究2】我们知道:两点确定一条直线,进而它的倾斜角也就确定了,那么任给直线l上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),直线l的倾斜角α与P1,P2两点的坐标有什么样的内在联系呢?请用向量法探究下列问题:
(1)已知直线l经过O(0,0),P(1,1),α与O,P的坐标有什么关系?
(2)类似地,如果直线l经过P1(1,0),P2(-1,2),α与P1,P2的坐标有什么关系?
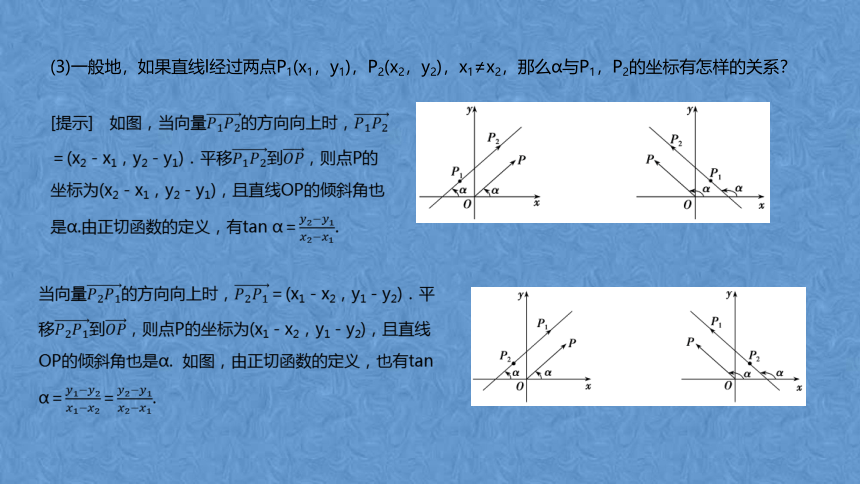
(3)一般地,如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,那么α与P1,P2的坐标有怎样的关系?
(二)倾斜角与斜率
◆(1)直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2),x1≠x2 的坐标有如下关系:tan α= .
(2)我们把一条直线的倾斜角α的 叫做这条直线的斜率.常用小写字母k表示,即k= .
(3)倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度,它们的对应关系:
所有的直线都有倾斜角;
不是所有的直线都存在斜率。
正切值
tanα
定义:我们把一条直线的的倾斜角的正切值叫做
这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
倾斜角是90 °的直线没有斜率。
我们也可以用斜率表示直线的倾斜程度。
即x每增加一个单位,y增加k个单位。
倾斜角
斜率
如何描述这二者的关系呢?
60o
135o
-1
30o
150o
a
k
O
a
tan
=
k
斜率单调递增
斜率单调递增
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
判断正误:
③任一条直线都有倾斜角,所以任一条直线都有
斜率. ( )
①直线的倾斜角为α,则直线的斜率为 ( )
④直线的倾斜角越大,则直线的斜率越大 ( )
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 ( )
②直线的斜率的范围是 ( )
√
思考1:
C
练习:判断三条直线斜率的大小关系
①
②
③
A.k1C.k3当倾斜角a∈[0°,90°)时,斜率为零和正数,角度越大,斜率越大。
当倾斜角a∈[0°,90°)时,斜率为负数,角度越大,斜率越大。
A
想一想
我们知道,两点也可以唯一确定一条直线。
问题:
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?
如图,当α为锐角时,
锐角
探究新知:由两点确定的直线的斜率
能不能构造一个直角三角形去求?
如图,当α为钝角时,
钝角
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢
想一想
3、直线的斜率公式:
综上所述,我们得到经过两点
的直线斜率公式:
1、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,K=0
对公式的
深入理解
2、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:斜率不存在, 因为分母为0。
对公式的
深入理解
如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、BC、CA的斜率,并判断这 些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
直线AB的斜率
直线BC的斜率
直线CA的斜率
∵
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角。
解:
∵
∴直线AB的倾斜角为零度角。
∵
例1
例2:
2、已知三点A(a,2),B(5,1),C(-4,2a)在同一直线上,求a的值
1、 求证:A(-2,8) B(3,-2) C(1,2)三点
在同一直线上.
例3:
2、 已知两点A(2,3)、B(3,0),过点P(-1,0)的直线与线段AB有公共点.求直线的斜率k的取值范围.
若B(-3,1), B(3,-1),则k的取值范围为?
例4:
N(-8,3)
M(2,2)
因为入射角等于反射角
)
0
,
2
(
P
-
\
反射点
(
)
的坐标
求反射点
后过点
轴反射
经过
射出一条光线
从
P
,
)
3
,
8
(
N
x
,
2
,
2
M
-
思考交流
O
x
y
2
2
-2
P
或利用光线性质:
N(-8,3),P(x,0),M1(2,-2)三点共线。
注意:体会分式可能具有几何性质:斜率
糖水加糖糖水变甜了
真分数性质
2022-2023学年高中数学选择性必修2教学课件
知识回顾:
我们学过:y=x+1,它表示什么?
如何在平面直角坐标系内确定它的位置
y
1
x
o
-1
对于平面直角坐标系内的一条直线 l ,它的位置由哪些条件确定?
x
y
O
l
问题引入
我们知道,两点确定一条直线.一点能确定一条直线的位置吗?已知直线 l 经过点P,直线 l 的位置能够确定吗?
问题引入
x
y
O
l
l’
l’’
P
过一点P可以作无数条直线l 1, l 2 , l 3 ,…它们都经过点P (组成一个直线束),这些直线区别在哪里呢?
问题引入
x
y
O
l
l’
l’’
P
容易看出,它们的倾斜程度不同.怎样描述直线的倾斜程度呢?
问题引入
x
y
O
l
l’
l’’
P
x
y
o
l
α
定义:在平面直角坐标系中,对于一条与x轴相交的直线l,把x轴的正方向按逆时针绕交点旋转到和直线l重合所成的角,叫做直线的倾斜角。
规定:直线和x轴平行或重合时,它的倾斜角为0°
)
180
,
0
[
o
o
a
倾斜角范围
P
知识点2 直线的倾斜角
下列四图中,表示直线的倾斜角的是( )
练习:
A
B
C
D
A
特别地,当直线和x轴平行或重合时,
它的倾斜角为0°。
直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。
坐标平面上任何一条直都有唯一的倾斜角。
倾斜角的取值范围是:
)
180
,
0
[
o
o
a
思考: 日常生活中,还有没有刻画倾斜程度的量?
如图,日常生活中,我们经常用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即
升高量
前进量
A
B
C
D
可理解为:在水平方向移动1km,在铅直方向上升或下降的数值(km),这个比值表示了坡度的大小。刻画了道路等的倾斜程度。
知识点2 斜率
【探究2】我们知道:两点确定一条直线,进而它的倾斜角也就确定了,那么任给直线l上两点P1(x1,y1),P2(x2,y2)(其中x1≠x2),直线l的倾斜角α与P1,P2两点的坐标有什么样的内在联系呢?请用向量法探究下列问题:
(1)已知直线l经过O(0,0),P(1,1),α与O,P的坐标有什么关系?
(2)类似地,如果直线l经过P1(1,0),P2(-1,2),α与P1,P2的坐标有什么关系?
(3)一般地,如果直线l经过两点P1(x1,y1),P2(x2,y2),x1≠x2,那么α与P1,P2的坐标有怎样的关系?
(二)倾斜角与斜率
◆(1)直线l的倾斜角α与直线l上的两点P1(x1,y1),P2(x2,y2),x1≠x2 的坐标有如下关系:tan α= .
(2)我们把一条直线的倾斜角α的 叫做这条直线的斜率.常用小写字母k表示,即k= .
(3)倾斜角和斜率分别从形和数两个角度刻画了直线相对于x轴的倾斜程度,它们的对应关系:
所有的直线都有倾斜角;
不是所有的直线都存在斜率。
正切值
tanα
定义:我们把一条直线的的倾斜角的正切值叫做
这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
倾斜角是90 °的直线没有斜率。
我们也可以用斜率表示直线的倾斜程度。
即x每增加一个单位,y增加k个单位。
倾斜角
斜率
如何描述这二者的关系呢?
60o
135o
-1
30o
150o
a
k
O
a
tan
=
k
斜率单调递增
斜率单调递增
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
判断正误:
③任一条直线都有倾斜角,所以任一条直线都有
斜率. ( )
①直线的倾斜角为α,则直线的斜率为 ( )
④直线的倾斜角越大,则直线的斜率越大 ( )
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 ( )
②直线的斜率的范围是 ( )
√
思考1:
C
练习:判断三条直线斜率的大小关系
①
②
③
A.k1
当倾斜角a∈[0°,90°)时,斜率为负数,角度越大,斜率越大。
A
想一想
我们知道,两点也可以唯一确定一条直线。
问题:
如果知道直线上的两点,怎么样来求直线的斜率(倾斜角)呢?
如图,当α为锐角时,
锐角
探究新知:由两点确定的直线的斜率
能不能构造一个直角三角形去求?
如图,当α为钝角时,
钝角
x
y
o
(3)
y
o
x
(4)
当 的位置对调时, 值又如何呢
想一想
3、直线的斜率公式:
综上所述,我们得到经过两点
的直线斜率公式:
1、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?
答:成立,因为分子为0,分母不为0,K=0
对公式的
深入理解
2、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
答:斜率不存在, 因为分母为0。
对公式的
深入理解
如图,已知A(4,2)、B(-8,2)、C(0,-2),求直线AB、BC、CA的斜率,并判断这 些直线的倾斜角是什么角?
y
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
直线AB的斜率
直线BC的斜率
直线CA的斜率
∵
∴直线CA的倾斜角为锐角
∴直线BC的倾斜角为钝角。
解:
∵
∴直线AB的倾斜角为零度角。
∵
例1
例2:
2、已知三点A(a,2),B(5,1),C(-4,2a)在同一直线上,求a的值
1、 求证:A(-2,8) B(3,-2) C(1,2)三点
在同一直线上.
例3:
2、 已知两点A(2,3)、B(3,0),过点P(-1,0)的直线与线段AB有公共点.求直线的斜率k的取值范围.
若B(-3,1), B(3,-1),则k的取值范围为?
例4:
N(-8,3)
M(2,2)
因为入射角等于反射角
)
0
,
2
(
P
-
\
反射点
(
)
的坐标
求反射点
后过点
轴反射
经过
射出一条光线
从
P
,
)
3
,
8
(
N
x
,
2
,
2
M
-
思考交流
O
x
y
2
2
-2
P
或利用光线性质:
N(-8,3),P(x,0),M1(2,-2)三点共线。
注意:体会分式可能具有几何性质:斜率
糖水加糖糖水变甜了
真分数性质
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
