2022—2023学年人教版数学九年级上册22.1.2二次函数y=ax2的图象和性质 同步练习 (word版、含答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册22.1.2二次函数y=ax2的图象和性质 同步练习 (word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 15:42:04 | ||
图片预览



文档简介
2022-2023学年度人教版九年级数学章节培优训练试卷
班级 姓名
22.1 二次函数的图象和性质
22.1.2 二次函数y=ax2的图象和性质
一、选择题
1. 若二次函数y=mx2(m≠0)的图象经过点(2,-5),则它也经过点( )
A.(-2,-5) B.(-2,5) C.(2,5) D.(-5,2)
2. 关于抛物线y=3x2,下列说法正确的是( )
A.开口向下 B.顶点坐标为(0,3)
C.对称轴为y轴 D.当x<0时,y随x的增大而增大
3. 当ab>0时,关于x的二次函数y=ax2与一次函数y=ax+b的图象大致是( )
A B C D
已知点A(-2,y1),B(1,y2),C(3,y3)在二次函数y=-2x2的图象上,则y1,y2,y3的大小关系是( )
A.y15.已知二次函数y=(a-1)x2,当x>0时,y随x增大而增大,则实数a的取值范围是( )
A.a>0 B.a>1 C.a≠1 D.a<1
6.已知点A(x1,y1),B(x2,y2),C(x3,y3)都在二次函数y=ax2(a<0)的图象上,且x1A.y1C.y17.二次函数y=x2,当1≤y≤9时,自变量x的取值范围是( )
A.1≤x≤3 B.-3≤x≤3
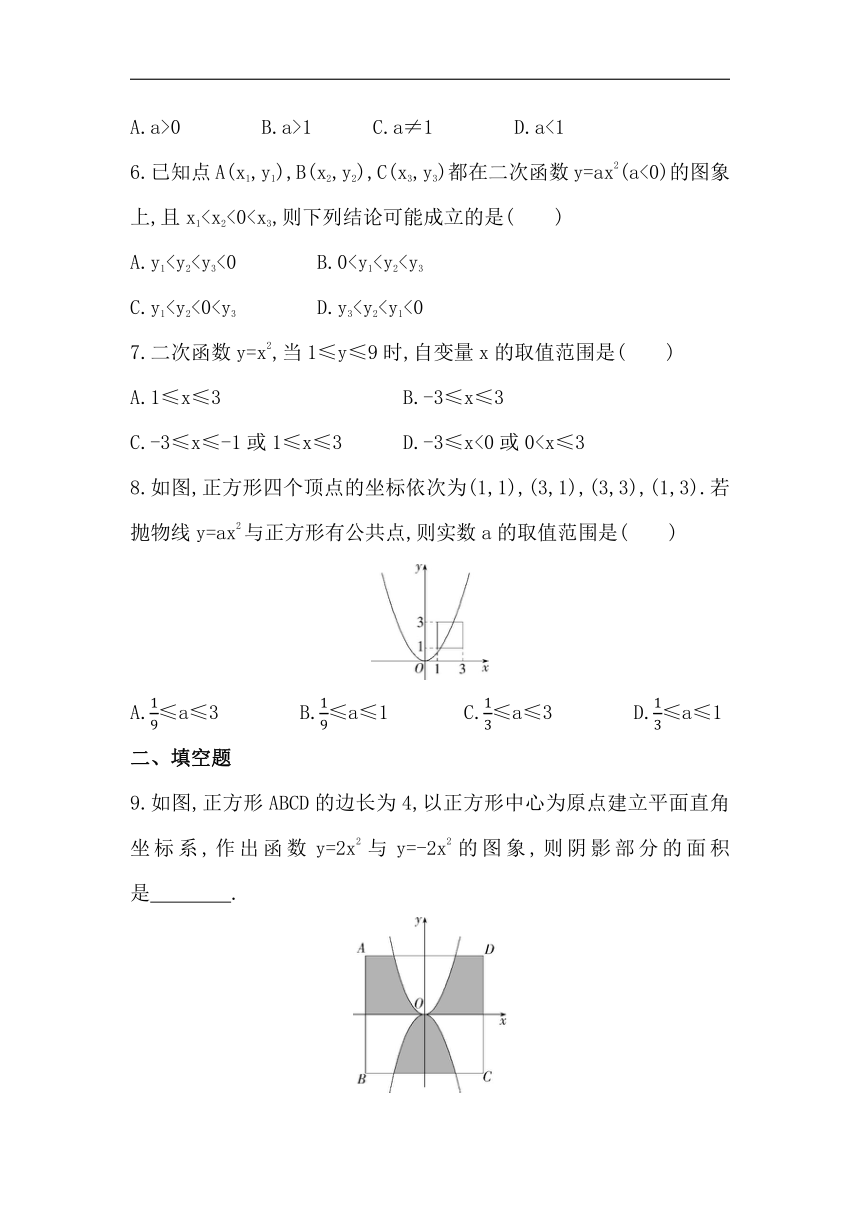
C.-3≤x≤-1或1≤x≤3 D.-3≤x<0或08.如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A.≤a≤3 B.≤a≤1 C.≤a≤3 D.≤a≤1
二、填空题
9.如图,正方形ABCD的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 .
10如图所示的四个二次函数的图象,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为 .
11如图,正方形OABC的顶点B恰好在函数y=ax2(a>0)的图象上,若正方形OABC的边长为,且边OA与x轴的正半轴的夹角为15°,则a的值为 .
三、解答题
12.已知二次函数y=ax2的图象经过点(-1,1).
(1)求这个二次函数的解析式;
(2)求当x=2时,y的值.
13.根据下列条件求m的取值范围.
(1)函数y=(m+3)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大;
(2)函数y=(2m-1)x2有最小值.
14.已知y=(k+2)是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求函数图象的顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减小.
答案全解全析
一、选择题
1.答案 A ∵y=mx2,∴抛物线的对称轴为y轴,∵图象经过点(2,-5),∴图象也经过点(-2,-5).故选A.
2.答案 C ∵y=3x2,∴抛物线开口向上,对称轴为y轴,顶点坐标是(0,0),∴选项A、B都错误,选项C正确;∵a=3>0,对称轴为直线x=0,∴当x<0时,y随x的增大而减小,∴选项D错误.故选C.
3.答案 D ∵ab>0,∴a、b同号,当a>0时,b>0,抛物线y=ax2开口向上,过原点,直线y=ax+b过第一、二、三象限,没有选项符合;当a<0时,b<0,抛物线y=ax2开口向下,过原点,直线y=ax+b过第二、三、四象限,此时D选项符合.故选D.
4.答案 D ∵二次函数y=-2x2的图象的对称轴是y轴,图象开口向下,∴当x>0时,y随x的增大而减小,又∵点A(-2,y1)关于y轴的对称点为(2,y1),0<1<2<3,∴y35. 答案 B ∵二次函数y=(a-1)x2,当x>0时,y随x增大而增大,∴a-1>0,∴a>1.
6. 答案 A ∵二次函数y=ax2图象的对称轴为y轴,开口向下,∴当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.∵x17. 答案 C ∵y=x2,∴该函数图象开口向上,对称轴为y轴,当x>0时,y随x的增大而增大,当x<0时,y随x的增大而减小.∵当y=1时,x=±1;当y=9时,x=±3,∴当1≤y≤9时,自变量x的取值范围是-3≤x≤-1或1≤x≤3.
8. 答案 A 当抛物线经过(1,3)时,a=3;当抛物线经过(3,1)时,a=.若抛物线y=ax2与正方形有公共点,则≤a≤3,故选A.
二、填空题
9.答案 8
解析 ∵函数y=2x2与y=-2x2的图象关于x轴对称,∴题图中阴影部分的面积是边长为4的正方形面积的一半,∴题图中阴影部分的面积是×42=8.
10.答案 a>b>d>c(或c解析 如图,作直线x=1与四条抛物线相交,可知直线x=1与四条抛物线的交点从上到下依次为(1,a),(1,b),(1,d),(1,c),所以a>b>d>c(或c11.
解析 如图,连接OB,过B作BD⊥x轴于D,则∠BOA=45°,∠BOD=60°,已知正方形的边长为,则OB=2.Rt△OBD中,OB=2,∠BOD=60°,则∠OBD=30°,∴OD=OB=1,∴BD=,故B(1,),将B(1,)代入y=ax2中,得a=.
三、解答题
12.解析 (1)把(-1,1)代入y=ax2,得a·(-1)2=1,解得a=1,
所以这个二次函数的解析式为y=x2.
(2)当x=2时,y=x2=4.
13.解析 (1)∵函数y=(m+3)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大,
∴m+3<0,
解得m<-3.
(2)∵函数y=(2m-1)x2有最小值,
∴2m-1>0,
解得m>.
14.解析 (1)∵y=(k+2)是二次函数,
∴k2+k-4=2且k+2≠0,
∴k=-3或k=2,
∵函数图象有最高点,∴函数图象的开口向下,
∴k+2<0,解得k<-2,
∴k=-3.
(2)当k=-3时,y=-x2,∴函数图象的顶点坐标为(0,0),对称轴为y轴,
∴当x>0时,y随x的增大而减小.
班级 姓名
22.1 二次函数的图象和性质
22.1.2 二次函数y=ax2的图象和性质
一、选择题
1. 若二次函数y=mx2(m≠0)的图象经过点(2,-5),则它也经过点( )
A.(-2,-5) B.(-2,5) C.(2,5) D.(-5,2)
2. 关于抛物线y=3x2,下列说法正确的是( )
A.开口向下 B.顶点坐标为(0,3)
C.对称轴为y轴 D.当x<0时,y随x的增大而增大
3. 当ab>0时,关于x的二次函数y=ax2与一次函数y=ax+b的图象大致是( )
A B C D
已知点A(-2,y1),B(1,y2),C(3,y3)在二次函数y=-2x2的图象上,则y1,y2,y3的大小关系是( )
A.y1
A.a>0 B.a>1 C.a≠1 D.a<1
6.已知点A(x1,y1),B(x2,y2),C(x3,y3)都在二次函数y=ax2(a<0)的图象上,且x1
A.1≤x≤3 B.-3≤x≤3
C.-3≤x≤-1或1≤x≤3 D.-3≤x<0或0
A.≤a≤3 B.≤a≤1 C.≤a≤3 D.≤a≤1
二、填空题
9.如图,正方形ABCD的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=-2x2的图象,则阴影部分的面积是 .
10如图所示的四个二次函数的图象,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为 .
11如图,正方形OABC的顶点B恰好在函数y=ax2(a>0)的图象上,若正方形OABC的边长为,且边OA与x轴的正半轴的夹角为15°,则a的值为 .
三、解答题
12.已知二次函数y=ax2的图象经过点(-1,1).
(1)求这个二次函数的解析式;
(2)求当x=2时,y的值.
13.根据下列条件求m的取值范围.
(1)函数y=(m+3)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大;
(2)函数y=(2m-1)x2有最小值.
14.已知y=(k+2)是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求函数图象的顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减小.
答案全解全析
一、选择题
1.答案 A ∵y=mx2,∴抛物线的对称轴为y轴,∵图象经过点(2,-5),∴图象也经过点(-2,-5).故选A.
2.答案 C ∵y=3x2,∴抛物线开口向上,对称轴为y轴,顶点坐标是(0,0),∴选项A、B都错误,选项C正确;∵a=3>0,对称轴为直线x=0,∴当x<0时,y随x的增大而减小,∴选项D错误.故选C.
3.答案 D ∵ab>0,∴a、b同号,当a>0时,b>0,抛物线y=ax2开口向上,过原点,直线y=ax+b过第一、二、三象限,没有选项符合;当a<0时,b<0,抛物线y=ax2开口向下,过原点,直线y=ax+b过第二、三、四象限,此时D选项符合.故选D.
4.答案 D ∵二次函数y=-2x2的图象的对称轴是y轴,图象开口向下,∴当x>0时,y随x的增大而减小,又∵点A(-2,y1)关于y轴的对称点为(2,y1),0<1<2<3,∴y3
6. 答案 A ∵二次函数y=ax2图象的对称轴为y轴,开口向下,∴当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.∵x1
8. 答案 A 当抛物线经过(1,3)时,a=3;当抛物线经过(3,1)时,a=.若抛物线y=ax2与正方形有公共点,则≤a≤3,故选A.
二、填空题
9.答案 8
解析 ∵函数y=2x2与y=-2x2的图象关于x轴对称,∴题图中阴影部分的面积是边长为4的正方形面积的一半,∴题图中阴影部分的面积是×42=8.
10.答案 a>b>d>c(或c
解析 如图,连接OB,过B作BD⊥x轴于D,则∠BOA=45°,∠BOD=60°,已知正方形的边长为,则OB=2.Rt△OBD中,OB=2,∠BOD=60°,则∠OBD=30°,∴OD=OB=1,∴BD=,故B(1,),将B(1,)代入y=ax2中,得a=.
三、解答题
12.解析 (1)把(-1,1)代入y=ax2,得a·(-1)2=1,解得a=1,
所以这个二次函数的解析式为y=x2.
(2)当x=2时,y=x2=4.
13.解析 (1)∵函数y=(m+3)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大,
∴m+3<0,
解得m<-3.
(2)∵函数y=(2m-1)x2有最小值,
∴2m-1>0,
解得m>.
14.解析 (1)∵y=(k+2)是二次函数,
∴k2+k-4=2且k+2≠0,
∴k=-3或k=2,
∵函数图象有最高点,∴函数图象的开口向下,
∴k+2<0,解得k<-2,
∴k=-3.
(2)当k=-3时,y=-x2,∴函数图象的顶点坐标为(0,0),对称轴为y轴,
∴当x>0时,y随x的增大而减小.
同课章节目录
