苏科版七年级上册 第2章 有理数 课件(28张)
文档属性
| 名称 | 苏科版七年级上册 第2章 有理数 课件(28张) |  | |
| 格式 | ppt | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 16:33:20 | ||
图片预览








文档简介
(共28张PPT)
有理数
本章总结提升
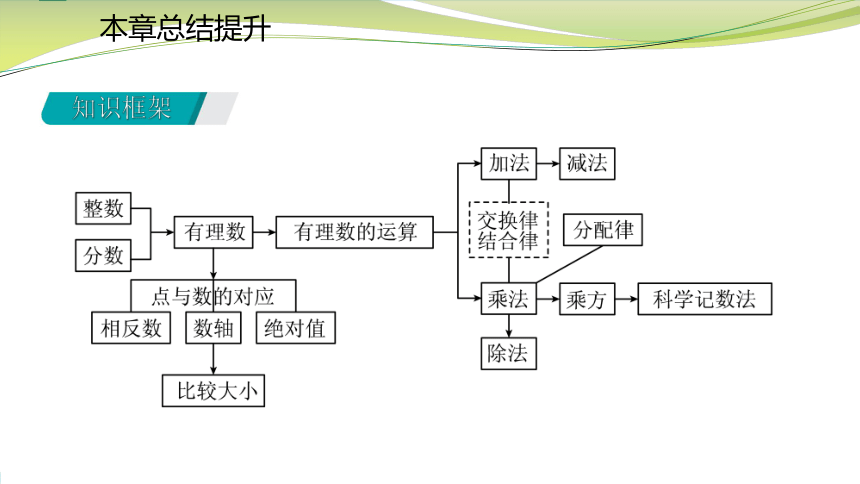
知识框架
整合提升
问题1 有理数的概念及分类
本章总结提升
引入负数后,数的范围扩大到了有理数,你能用图表示有理数的分类吗?在分类时应该注意什么?
本章总结提升
本章总结提升
【归纳总结】有理数的分类方法有两种:
一是逐个考察给出的数,看它是什么数,即是否属于某一集合,如属于,就可以填入相应的大括号内;二是从给出的数中找出属于这个集合的数,逐个填入相应的大括号内,如在填负整数集合时,只要从给出的数中找出所有的负整数,并填入相应的大括号内即可.
问题2 利用数轴理解相反数、绝对值
本章总结提升
怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样利用数轴解释一个数的绝对值和相反数?
本章总结提升
C
例2 如图2-T-1,数轴上有A,B,C,D四个点,其中到原点距
离相等的两个点是( )
A.点B与点D B.点A与点C
C.点A与点D D.点B与点C
图2-T-1
[解析] 由数轴可得:点A表示的数为-2,点D表示的数为2,
根据数轴上表示数a的点与表示数-a的点到原点的距离相等,
∴点A与点D到原点的距离相等.故选C.
本章总结提升
【归纳总结】有理数可以用数轴上的点来表示,数轴是有原点、正方向和单位长度的直线.一个数的绝对值是数轴上表示该数的点到原点的距离;表示互为相反数的两点在原点两侧,且到原点的距离相等.利用数形结合思想可以使所要研究的问题化难为易,化繁为简.
问题3 有理数的大小比较
本章总结提升
有理数的大小比较方法有几种?数轴上的两个有理数,哪个大?对于绝对值不相等的两个负数,哪个小?
本章总结提升
例3 已知a>0,b<0,且|b|>|a|,则a,-a,b,-b按从小到大的顺序排列为( )
A.-b<a<-a<b B.b<-a<a<-b
C.a<-a<-b<b D.-a<a<b<-b
B
本章总结提升
[解析] 方法一:根据有理数比较大小的法则进行比较即可.
∵a>0,b<0,且|b|>|a|,∴-b>a>0,b<-a<0,∴b<-a<a<-b.故选B.
方法二:利用数轴比较大小.
由a>0,b<0可知a为正数,b为负数,a,b所对应的点分别在数轴上原点的右边和左边,而|b|>|a|,所以表示数a的点到原点的距离比表示数b的点到原点的距离近,再根据相反数的意义可在数轴上表示a,-a,b,-b为:
故a,-a,b,-b按从小到大的顺序排列为b<-a<a<-b.故选B.
本章总结提升
【归纳总结】有理数的大小比较有两种方法:
一是利用有理数比较大小的法则比较;二是借助数轴把这些数对应的点表示出来,按从左到右的顺序确定后,就能知道这些数的大小关系.本例题还可以通过特殊值法进行比较,同学们请试一试.
问题4 有理数的混合运算
本章总结提升
引入负数后,减法中哪些原来不能进行的运算可以进行了?有理数的加法与减法,乘法与除法各有什么关系?有理数的混合运算都能转化为加法与乘法运算吗?有理数有哪些运算律?结合例子说明运算律在有理数运算中的作用.
本章总结提升
[解析] (1)本题直接算括号内的比较麻烦,注意到乘数36是被乘数各分母的公倍数,运用乘法分配律可以去掉所有的分母.
本章总结提升
本章总结提升
【归纳总结】有理数混合运算的四种运算技巧:
(1)转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算;
(2)凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合求解;
本章总结提升
(3)分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算;
(4)巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
本章总结提升
例5 王先生到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,王先生从1楼出发,电梯上下楼层依次记录如下(单位:层):+6,-3,+10,-8,+12,-7,-10.
(1)请你通过计算说明王先生最后是否回到出发点1楼;
(2)该中心大楼每层高3 m,电梯每向上或下1 m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯共耗电多少度.
本章总结提升
解:(1)(+6)+(-3)+(+10)+(-8)+(+12)+(-7)+(-10)
=6-3+10-8+12-7-10
=28-28
=0,
∴王先生最后回到出发点1楼.
(2)3×(|+6|+|-3|+|+10|+|-8|+|+12|+|-7|+|-10|)
=3×(6+3+10+8+12+7+10)
=3×56
=168(m),
∴他办事时电梯共耗电168×0.1=16.8(度).
问题5 科学记数法
本章总结提升
把一个大于10的数写成a×10n的形式,a可以大于10吗?当原数大于等于10时,如何确定n
本章总结提升
例6 (1)[2017·山西]2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计,仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为( )
A.186×108吨 B.18.6×109吨
C.1.86×1010吨 D.0.186×1011吨
C
本章总结提升
(2)[2017·达州]达州市莲花湖湿地公园占地面积用科学记数法表示为7.92×106平方米,则原数为__________平方米.
7920000
本章总结提升
【归纳总结】科学记数法的表示形式为a×10n,其中1≤|a|<10,n为正整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.用科学记数法表示的数,原数是多少,只看10的指数n是几,小数点向右移动几位即可.
解:
本章总结提升
解:
解:设S= 5+8+11++14+17+·····+32
反过来写S=32+29+26+······+5
2S=(5+32)+(8+29)+·······(32+5)
=37X10
=370
所以S=185
例9:5+8+11++14+17+·····+32
分析:可利用“倒写相加”的方法来计算上式的和
分析:
证明:
设“ ”是一种运算符号,对任意两数x、y,有:
其中a是一个不等于0的常数。
(1)验证:
(2)
的值。
有理数
本章总结提升
知识框架
整合提升
问题1 有理数的概念及分类
本章总结提升
引入负数后,数的范围扩大到了有理数,你能用图表示有理数的分类吗?在分类时应该注意什么?
本章总结提升
本章总结提升
【归纳总结】有理数的分类方法有两种:
一是逐个考察给出的数,看它是什么数,即是否属于某一集合,如属于,就可以填入相应的大括号内;二是从给出的数中找出属于这个集合的数,逐个填入相应的大括号内,如在填负整数集合时,只要从给出的数中找出所有的负整数,并填入相应的大括号内即可.
问题2 利用数轴理解相反数、绝对值
本章总结提升
怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样利用数轴解释一个数的绝对值和相反数?
本章总结提升
C
例2 如图2-T-1,数轴上有A,B,C,D四个点,其中到原点距
离相等的两个点是( )
A.点B与点D B.点A与点C
C.点A与点D D.点B与点C
图2-T-1
[解析] 由数轴可得:点A表示的数为-2,点D表示的数为2,
根据数轴上表示数a的点与表示数-a的点到原点的距离相等,
∴点A与点D到原点的距离相等.故选C.
本章总结提升
【归纳总结】有理数可以用数轴上的点来表示,数轴是有原点、正方向和单位长度的直线.一个数的绝对值是数轴上表示该数的点到原点的距离;表示互为相反数的两点在原点两侧,且到原点的距离相等.利用数形结合思想可以使所要研究的问题化难为易,化繁为简.
问题3 有理数的大小比较
本章总结提升
有理数的大小比较方法有几种?数轴上的两个有理数,哪个大?对于绝对值不相等的两个负数,哪个小?
本章总结提升
例3 已知a>0,b<0,且|b|>|a|,则a,-a,b,-b按从小到大的顺序排列为( )
A.-b<a<-a<b B.b<-a<a<-b
C.a<-a<-b<b D.-a<a<b<-b
B
本章总结提升
[解析] 方法一:根据有理数比较大小的法则进行比较即可.
∵a>0,b<0,且|b|>|a|,∴-b>a>0,b<-a<0,∴b<-a<a<-b.故选B.
方法二:利用数轴比较大小.
由a>0,b<0可知a为正数,b为负数,a,b所对应的点分别在数轴上原点的右边和左边,而|b|>|a|,所以表示数a的点到原点的距离比表示数b的点到原点的距离近,再根据相反数的意义可在数轴上表示a,-a,b,-b为:
故a,-a,b,-b按从小到大的顺序排列为b<-a<a<-b.故选B.
本章总结提升
【归纳总结】有理数的大小比较有两种方法:
一是利用有理数比较大小的法则比较;二是借助数轴把这些数对应的点表示出来,按从左到右的顺序确定后,就能知道这些数的大小关系.本例题还可以通过特殊值法进行比较,同学们请试一试.
问题4 有理数的混合运算
本章总结提升
引入负数后,减法中哪些原来不能进行的运算可以进行了?有理数的加法与减法,乘法与除法各有什么关系?有理数的混合运算都能转化为加法与乘法运算吗?有理数有哪些运算律?结合例子说明运算律在有理数运算中的作用.
本章总结提升
[解析] (1)本题直接算括号内的比较麻烦,注意到乘数36是被乘数各分母的公倍数,运用乘法分配律可以去掉所有的分母.
本章总结提升
本章总结提升
【归纳总结】有理数混合运算的四种运算技巧:
(1)转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算;
(2)凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合求解;
本章总结提升
(3)分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算;
(4)巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.
本章总结提升
例5 王先生到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,王先生从1楼出发,电梯上下楼层依次记录如下(单位:层):+6,-3,+10,-8,+12,-7,-10.
(1)请你通过计算说明王先生最后是否回到出发点1楼;
(2)该中心大楼每层高3 m,电梯每向上或下1 m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯共耗电多少度.
本章总结提升
解:(1)(+6)+(-3)+(+10)+(-8)+(+12)+(-7)+(-10)
=6-3+10-8+12-7-10
=28-28
=0,
∴王先生最后回到出发点1楼.
(2)3×(|+6|+|-3|+|+10|+|-8|+|+12|+|-7|+|-10|)
=3×(6+3+10+8+12+7+10)
=3×56
=168(m),
∴他办事时电梯共耗电168×0.1=16.8(度).
问题5 科学记数法
本章总结提升
把一个大于10的数写成a×10n的形式,a可以大于10吗?当原数大于等于10时,如何确定n
本章总结提升
例6 (1)[2017·山西]2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计,仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为( )
A.186×108吨 B.18.6×109吨
C.1.86×1010吨 D.0.186×1011吨
C
本章总结提升
(2)[2017·达州]达州市莲花湖湿地公园占地面积用科学记数法表示为7.92×106平方米,则原数为__________平方米.
7920000
本章总结提升
【归纳总结】科学记数法的表示形式为a×10n,其中1≤|a|<10,n为正整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.用科学记数法表示的数,原数是多少,只看10的指数n是几,小数点向右移动几位即可.
解:
本章总结提升
解:
解:设S= 5+8+11++14+17+·····+32
反过来写S=32+29+26+······+5
2S=(5+32)+(8+29)+·······(32+5)
=37X10
=370
所以S=185
例9:5+8+11++14+17+·····+32
分析:可利用“倒写相加”的方法来计算上式的和
分析:
证明:
设“ ”是一种运算符号,对任意两数x、y,有:
其中a是一个不等于0的常数。
(1)验证:
(2)
的值。
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
