苏科版七年级数学上册第3章代数式复习课件(共37张PPT)
文档属性
| 名称 | 苏科版七年级数学上册第3章代数式复习课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 803.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 16:45:53 | ||
图片预览










文档简介
(共37张PPT)
代数式
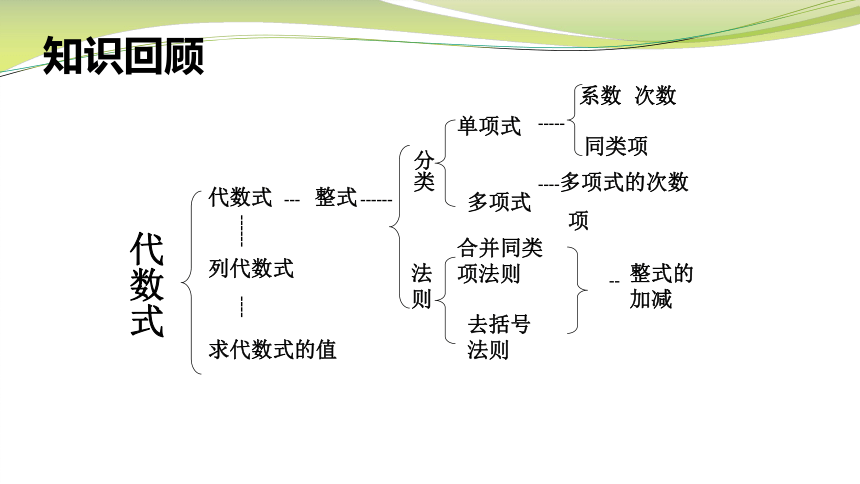
知识回顾
代数式
代数式
------
列代数式
----
求代数式的值
---
整式
------
法则
分类
单项式
多项式
合并同类项法则
去括号法则
--
整式的加减
-----
系数 次数
同类项
----多项式的次数
项
知识点 :
1. 代数式:用基本运算符号把数和字母连接而成的式子。
2. 单项式: 表示数与字母的积的代数式叫单项式。
单独一个数或一个字母也是单项式。
其中的数字因数叫单项式的系数, 所有的字母的指数的和叫单项式的次数。
3. 多项式:几个单项式的和叫做多项式,
次数最高项的次数叫做这个多项式的次数。
单项式和多项式统称为整式。
(2)数字与字母相乘,数字通常写在字母前面;
(1) a×b 通常写作 a·b 或 ab ;
如1÷a 通常写作 ;
如:a×3通常写作3a
(3)带分数因数一般写成假分数.
如: ×a 通常写作 a
代数式的规范写法:
{
(4)数字与数字相乘,一般仍用“×”号,即“×”号不能省略
(5)除法运算写成分数形式。
(6)相同的字母写成乘方的形式
如aaa写作a3
一、填空,
(1)正方体的边长为a ㎝,则它的表面积是____c㎡,体积是______ ;
(2)温度由t ℃上升5 ℃后是_____℃;
6a2
a3
(t+5)
(3)小民今年a 岁,前年他_____岁;
(4)如果n 表示任意一个整数,则奇数可表示为_____,偶数可表______
(a-2)
2n+1
2n
(5)苹果 每千克a 元,香蕉 每千克b 元,买5 斤苹果,8 斤香蕉,一共需付______ 元;
(6)一件衬衣打八折后售价为m 元,
则此上衣原价为______元;
(5a+8b)
(7)一个边长为a 的正方形与一个长为b 的长方形,它们的面积相等,则这个
长方形的宽为_____;
(8)如果x是一个两位数,现在把8 放在它的右边,得到一个三位数是_____。
10x+8
单项式 a -xy
系数
二、填表
1
-1
注意:系数包括前面的符号。
二、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
三、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
单项式 a -xy
系数
二、填表
1
-1
注意:系数包括前面的符号。
二、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
三、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
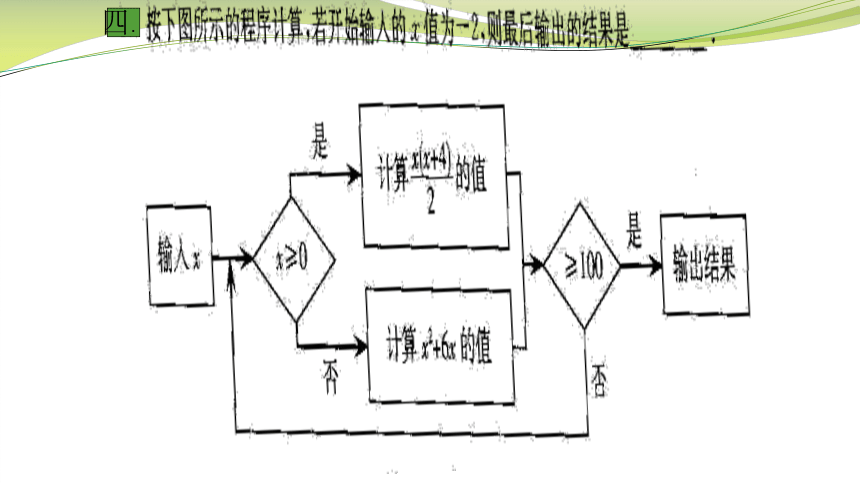
四.
在下列计算程序中填写适当的数 或转换 步骤.
输入-2
( )2
-5
输出
(1)
输入 x
输出
( )2
×3
-5
(2)
输入
输出11
+2
-5
-1
( )2
2或-6
(3)
注:给出程序,只需顺向计算, 先写的先算.
编写程序,必须逆向分析,先算的先写.
(1)已知 =3,求 - 的值.
(2)当 时,求代数式
的值.
整体代入
9.求代数式的值:
2x2y-3xy+x2-2x2y-1+5xy- x2,
其中x=2,y =-1
10.先化简再求值
-(8xy-3y2)+5xy-2(3xy-2x2)
其中x=-2,y =1
求代数式的值。
(1)当a=2,b=-3时,
求代数式 的值。
(2)当a=2,b=-3, 时,
求代数式 的值。
(1)所含的字母相同
(2)相同字母的指数也相同
(3)所有的常数项都是同类项
3.同类项的定义
填填看。
(1)、如果 是同类项,那么 。
(2)、如果 是同类项,那么 , 。
2
4
3
思 考
4.合并同类项的法则
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
合并同类项法则:把同类项的系数相加,所得的结果作
为系数,字母和字母的指数保持不变.
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
=5x2
=4x2
3x与2y不是同类项,不能合并。
问题
5.去括号的法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不改变.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变.
去括号法则
1、括号前面有“+”号,把括号和它前面的“+”号去掉,括号里各项的符号不改变;
2、括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。
填填看,你是用什么方法填
问题
(1) +(3X-2Y)=
(2) -(2X-1)=
(3) -3(2a-b)=
(4) 6x -4y=2( )
(5) –3x+3Y=-3( )
3X-2Y
3x-2Y
-6a+3b
-2X+1
X-Y
注意:①去括号时,考虑符号是否改变, ②不要漏乘括号里的项.
某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式:第一种:买一支毛笔附赠一本书法练习本;第二种:按购买金额打九折付款。八年级(5)班的小明想为本班书法兴趣小组购买这种毛笔10支,书法练习本 x(x≥10)本。
(1)用代数式分别表示两种购买方式应支付的金额.
(2)若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱?
解(1)第一种:10×25+5(x-10)=5x+200
第二种: (25×10+5x) ×90%=4.5x+225
(2)解:把X=30分别代入两个代数式: 5x+200=350
4.5x+225=360所以选择第一种优惠方式
填填选选
(1)2(3x-2y)= .
(2)-(a+b-c)= .
(3)-2a+1的相反数是 .
练一练
6x-4y
-a-b+c
2a-1
(1)下列各组代数式中,属于同类项的是( )
A、2x2y与2xy2 B、xy与-xy
C、2x与2xy D、2x2与2y2
(2)下列各式中,合并同类项正确的是( )
A、-a+3a=2 B、x2-2x2=-x
C、2x+x=3x D、3a+2b=5ab
(3)下列去括号,正确的是( )
A、-(a+b)=-a+b B、-(3x-2)=-3x-2
C、a2-(2a-1)=a2-2a+1 D、x-2(y-z)=x-2y+z
B
C
C
练一练
(1) 5a-(2a-4b)
(2) 2x2+3(2x-x2)
(3)(a2+2a)-2(a2+4a)
感觉怎么样
解:原式=5a-2a+4b=3a+4b
解 :原式=2x2+6x-3x2= -x2+6x
解原式=a2+2a-2a2-8a= -a2-6a
练一练
(1)先化简再求值2(a2-ab)-3(a2-ab)其中a= -2,b=3
(2)已知m-n=3,求4(m-n)-3m+3n+5的值
比较这二题有什么异同
解 :原式=2a2-2ab-3a2+3ab=-a2+ab
当a= -2,b=3时
-a2+ab =-(-2)2+(-2)×3=-4-6= -10
解:原式=4(m-n)-3(m-n)+5=(m-n)+5=3+5=8
直接代入
整体代入
练一练
生活中处处用得着数学
我国出租车收费标准因地而异,A市为:起步价10元,3千米后每千米价为1.2元;B市为:起步价8元,3千米后每千米价为1.4元。
试问(1)小王在A市、小李在B市都乘坐出租车8千米的费用相差多少元?
(2)小王在A市、小李在B市都乘坐出租车x千米(x>3)费用的和为多少元?
(3)小王在A市、小李在B市都乘坐出租车多少千米路程时,两人的车费一样多
探究题
练一练
1.化简
1. 4x-3(1-1.5x)+4(2-0.25x)
2. 9a3-[-6a2+2(a3- a2)]
2.若2xmy4与ax3y2n可以合并为一个
单项式,结果为-3x3y4,求a,m,n的值。
变式训练
3.小明在计算一个多项式减去 2x2y-3xy2-2y+1的2倍时,误
将减号看成了加号,结果等于4x2y+5xy2+3x-2y+5,
(1)求这个多项式.
(2)正确结果应该是什么
4.已知代数式
a,b取什么值时,此代数式的值与字母x取值无关?(不含X项)
6.已知:a2+ab=2,ab+b2=3, 求下列代数式的值: (1)a2+2ab+b2; (2)a2-b2.
解:(1) 原式=(a2 +ab)+(ab+b2)
=2+3
=5.
( 2 ) 原式=(a2+ab) -(ab+b2)
=2-3
=-1.
7.已知:a+b=5,a-c=4,
求代数式(b+c)2+2(b+c) -1的值.
解:(a+b) -(a-c)=5-4,
b+c=1;
当b+c=1时,
原式=12+2×1-1
=2.
8.已知一个多项式与a2-2a+1的和是a2 +a-1,求这个多项式。
9.已知A=2x2+y2+2z,B=x2-y2 +z ,求2A-B
10.若多项式mx3+3nxy2-2x3-xy2+y中不含三次项,求2m+3n的值.
11.若代数式a2+2kab+2b2-8ab-9
不含ab项,则k取何值?
代数式
知识回顾
代数式
代数式
------
列代数式
----
求代数式的值
---
整式
------
法则
分类
单项式
多项式
合并同类项法则
去括号法则
--
整式的加减
-----
系数 次数
同类项
----多项式的次数
项
知识点 :
1. 代数式:用基本运算符号把数和字母连接而成的式子。
2. 单项式: 表示数与字母的积的代数式叫单项式。
单独一个数或一个字母也是单项式。
其中的数字因数叫单项式的系数, 所有的字母的指数的和叫单项式的次数。
3. 多项式:几个单项式的和叫做多项式,
次数最高项的次数叫做这个多项式的次数。
单项式和多项式统称为整式。
(2)数字与字母相乘,数字通常写在字母前面;
(1) a×b 通常写作 a·b 或 ab ;
如1÷a 通常写作 ;
如:a×3通常写作3a
(3)带分数因数一般写成假分数.
如: ×a 通常写作 a
代数式的规范写法:
{
(4)数字与数字相乘,一般仍用“×”号,即“×”号不能省略
(5)除法运算写成分数形式。
(6)相同的字母写成乘方的形式
如aaa写作a3
一、填空,
(1)正方体的边长为a ㎝,则它的表面积是____c㎡,体积是______ ;
(2)温度由t ℃上升5 ℃后是_____℃;
6a2
a3
(t+5)
(3)小民今年a 岁,前年他_____岁;
(4)如果n 表示任意一个整数,则奇数可表示为_____,偶数可表______
(a-2)
2n+1
2n
(5)苹果 每千克a 元,香蕉 每千克b 元,买5 斤苹果,8 斤香蕉,一共需付______ 元;
(6)一件衬衣打八折后售价为m 元,
则此上衣原价为______元;
(5a+8b)
(7)一个边长为a 的正方形与一个长为b 的长方形,它们的面积相等,则这个
长方形的宽为_____;
(8)如果x是一个两位数,现在把8 放在它的右边,得到一个三位数是_____。
10x+8
单项式 a -xy
系数
二、填表
1
-1
注意:系数包括前面的符号。
二、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
三、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
单项式 a -xy
系数
二、填表
1
-1
注意:系数包括前面的符号。
二、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
三、下列式子哪些是单项式 哪些是多项式
(1)-1 (2)a=1 (3)3xy (4)-2a+4b
四.
在下列计算程序中填写适当的数 或转换 步骤.
输入-2
( )2
-5
输出
(1)
输入 x
输出
( )2
×3
-5
(2)
输入
输出11
+2
-5
-1
( )2
2或-6
(3)
注:给出程序,只需顺向计算, 先写的先算.
编写程序,必须逆向分析,先算的先写.
(1)已知 =3,求 - 的值.
(2)当 时,求代数式
的值.
整体代入
9.求代数式的值:
2x2y-3xy+x2-2x2y-1+5xy- x2,
其中x=2,y =-1
10.先化简再求值
-(8xy-3y2)+5xy-2(3xy-2x2)
其中x=-2,y =1
求代数式的值。
(1)当a=2,b=-3时,
求代数式 的值。
(2)当a=2,b=-3, 时,
求代数式 的值。
(1)所含的字母相同
(2)相同字母的指数也相同
(3)所有的常数项都是同类项
3.同类项的定义
填填看。
(1)、如果 是同类项,那么 。
(2)、如果 是同类项,那么 , 。
2
4
3
思 考
4.合并同类项的法则
同类项的系数相加,所得的结果作为系数,字母和字母的指数不变.
合并同类项法则:把同类项的系数相加,所得的结果作
为系数,字母和字母的指数保持不变.
下列各题合并同类项的结果对不对?若不对,请改正。
(1)、
(2)、
(3)、
(4)、
=5x2
=4x2
3x与2y不是同类项,不能合并。
问题
5.去括号的法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不改变.
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变.
去括号法则
1、括号前面有“+”号,把括号和它前面的“+”号去掉,括号里各项的符号不改变;
2、括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。
填填看,你是用什么方法填
问题
(1) +(3X-2Y)=
(2) -(2X-1)=
(3) -3(2a-b)=
(4) 6x -4y=2( )
(5) –3x+3Y=-3( )
3X-2Y
3x-2Y
-6a+3b
-2X+1
X-Y
注意:①去括号时,考虑符号是否改变, ②不要漏乘括号里的项.
某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式:第一种:买一支毛笔附赠一本书法练习本;第二种:按购买金额打九折付款。八年级(5)班的小明想为本班书法兴趣小组购买这种毛笔10支,书法练习本 x(x≥10)本。
(1)用代数式分别表示两种购买方式应支付的金额.
(2)若小明想为本班书法兴趣小组购买书法练习本30 本,试问小明应该选择哪一种优惠方式才更省钱?
解(1)第一种:10×25+5(x-10)=5x+200
第二种: (25×10+5x) ×90%=4.5x+225
(2)解:把X=30分别代入两个代数式: 5x+200=350
4.5x+225=360所以选择第一种优惠方式
填填选选
(1)2(3x-2y)= .
(2)-(a+b-c)= .
(3)-2a+1的相反数是 .
练一练
6x-4y
-a-b+c
2a-1
(1)下列各组代数式中,属于同类项的是( )
A、2x2y与2xy2 B、xy与-xy
C、2x与2xy D、2x2与2y2
(2)下列各式中,合并同类项正确的是( )
A、-a+3a=2 B、x2-2x2=-x
C、2x+x=3x D、3a+2b=5ab
(3)下列去括号,正确的是( )
A、-(a+b)=-a+b B、-(3x-2)=-3x-2
C、a2-(2a-1)=a2-2a+1 D、x-2(y-z)=x-2y+z
B
C
C
练一练
(1) 5a-(2a-4b)
(2) 2x2+3(2x-x2)
(3)(a2+2a)-2(a2+4a)
感觉怎么样
解:原式=5a-2a+4b=3a+4b
解 :原式=2x2+6x-3x2= -x2+6x
解原式=a2+2a-2a2-8a= -a2-6a
练一练
(1)先化简再求值2(a2-ab)-3(a2-ab)其中a= -2,b=3
(2)已知m-n=3,求4(m-n)-3m+3n+5的值
比较这二题有什么异同
解 :原式=2a2-2ab-3a2+3ab=-a2+ab
当a= -2,b=3时
-a2+ab =-(-2)2+(-2)×3=-4-6= -10
解:原式=4(m-n)-3(m-n)+5=(m-n)+5=3+5=8
直接代入
整体代入
练一练
生活中处处用得着数学
我国出租车收费标准因地而异,A市为:起步价10元,3千米后每千米价为1.2元;B市为:起步价8元,3千米后每千米价为1.4元。
试问(1)小王在A市、小李在B市都乘坐出租车8千米的费用相差多少元?
(2)小王在A市、小李在B市都乘坐出租车x千米(x>3)费用的和为多少元?
(3)小王在A市、小李在B市都乘坐出租车多少千米路程时,两人的车费一样多
探究题
练一练
1.化简
1. 4x-3(1-1.5x)+4(2-0.25x)
2. 9a3-[-6a2+2(a3- a2)]
2.若2xmy4与ax3y2n可以合并为一个
单项式,结果为-3x3y4,求a,m,n的值。
变式训练
3.小明在计算一个多项式减去 2x2y-3xy2-2y+1的2倍时,误
将减号看成了加号,结果等于4x2y+5xy2+3x-2y+5,
(1)求这个多项式.
(2)正确结果应该是什么
4.已知代数式
a,b取什么值时,此代数式的值与字母x取值无关?(不含X项)
6.已知:a2+ab=2,ab+b2=3, 求下列代数式的值: (1)a2+2ab+b2; (2)a2-b2.
解:(1) 原式=(a2 +ab)+(ab+b2)
=2+3
=5.
( 2 ) 原式=(a2+ab) -(ab+b2)
=2-3
=-1.
7.已知:a+b=5,a-c=4,
求代数式(b+c)2+2(b+c) -1的值.
解:(a+b) -(a-c)=5-4,
b+c=1;
当b+c=1时,
原式=12+2×1-1
=2.
8.已知一个多项式与a2-2a+1的和是a2 +a-1,求这个多项式。
9.已知A=2x2+y2+2z,B=x2-y2 +z ,求2A-B
10.若多项式mx3+3nxy2-2x3-xy2+y中不含三次项,求2m+3n的值.
11.若代数式a2+2kab+2b2-8ab-9
不含ab项,则k取何值?
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
