初中数学苏科版八年级上册 第一章 全等三角形 第1课时 复习课件(共22张)
文档属性
| 名称 | 初中数学苏科版八年级上册 第一章 全等三角形 第1课时 复习课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 613.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 19:19:29 | ||
图片预览





文档简介
(共22张PPT)
《全等三角形(1)》
基础梳理
性质
判定方法
一般三角形的判定
直角三角形的判定
已知两边对应相等
已知一边和一
角对应相等
已知两角对应相等
判定思路
全等三角形
性质
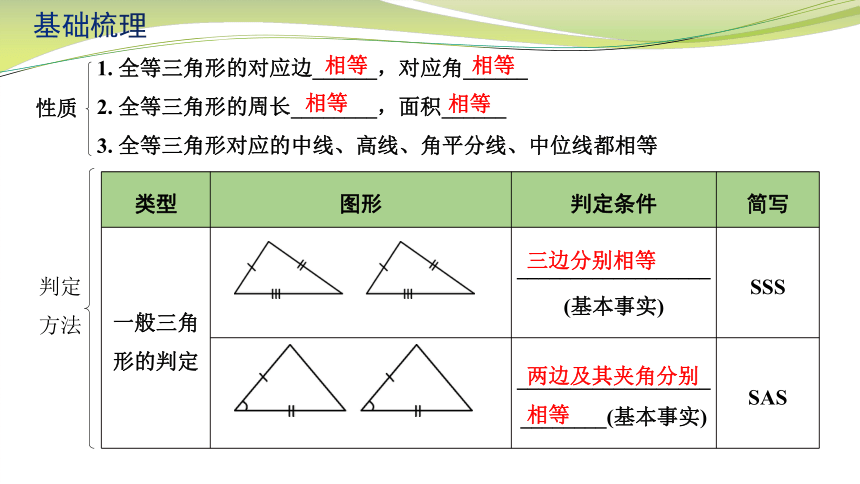
1. 全等三角形的对应边______,对应角______
2. 全等三角形的周长________,面积______
3. 全等三角形对应的中线、高线、角平分线、中位线都相等
判定方法
类型 图形 判定条件 简写
一般三角形的判定 __________________(基本事实) SSS
__________________________(基本事实) SAS
相等
相等
相等
相等
三边分别相等
两边及其夹角分别
相等
基础梳理
判定方法
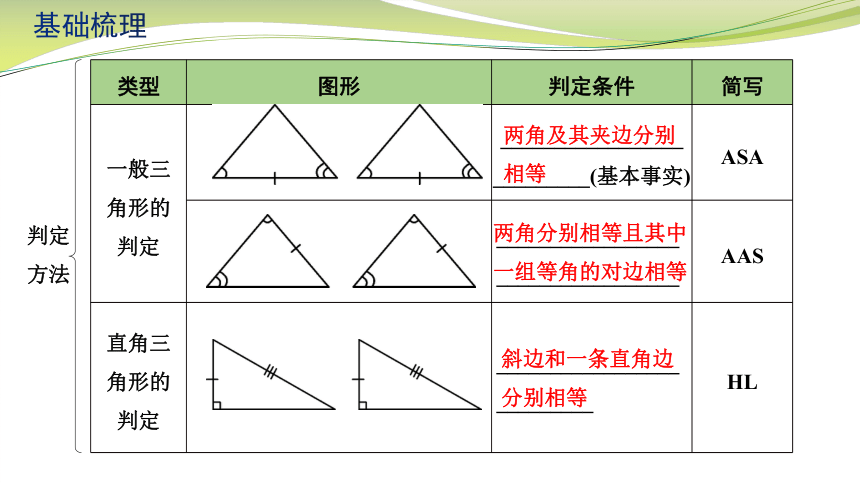
类型 图形 判定条件 简写
一般三角形的判定 __________________________(基本事实) ASA
__________________________________ AAS
直角三角形的判定 __________________________ HL
两角及其夹边分别
相等
斜边和一条直角边
分别相等
两角分别相等且其中一组等角的对边相等
基础梳理
判定思路
已知两边对应相等
找夹角→SAS
找第三边→SSS
已知一边和一
角对应相等
边为角的对边→找另一角→AAS
边为角的一边
找夹角的另一边→SAS
找夹边的另一角→ASA
找边的对角→AAS
已知两角
对应相等
找夹边→ASA
找一角的对边→AAS
基础梳理
经典例题:
例1.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=9,BC=5时,线段 AE的长为 ,
(2)已知∠D=35°,∠C=60°,求∠AFD的度数.
4
解:∵△ABC≌△DEB,∠C=60°(已知)
∴∠C=∠DBE=60°,∠A=∠D=35°(全等三角形对应角相等)
∵∠D+∠DBE+∠BED=180°(三角形内角和定理)
∠D=35°(已知)
∴∠ BED=180°-60°-35°=85°(等式性质)
∵ ∠BED+∠AEF=180° (平角定义)
∴ ∠AEF=95°(等式性质)
∴∠AFD=∠AEF+∠A=95°+35°=130°
(三角形一个外角等于与它不相邻的两个内角和)
策略总结:
已知:全等
对应元素:角
边
周长、面积
对应中线、
高线、
角平分线
中位线
……
全等三角形性质
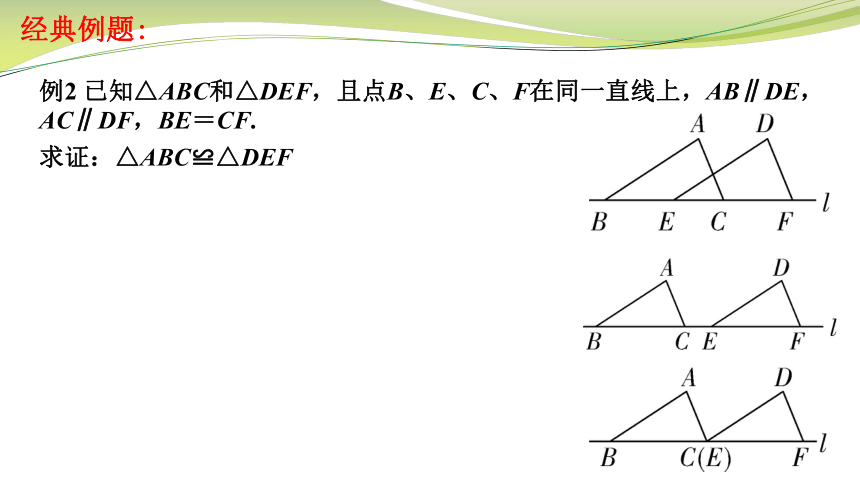
例2 已知△ABC和△DEF,且点B、E、C、F在同一直线上,AB∥DE,AC∥DF,BE=CF.
经典例题:
求证:△ABC≌△DEF
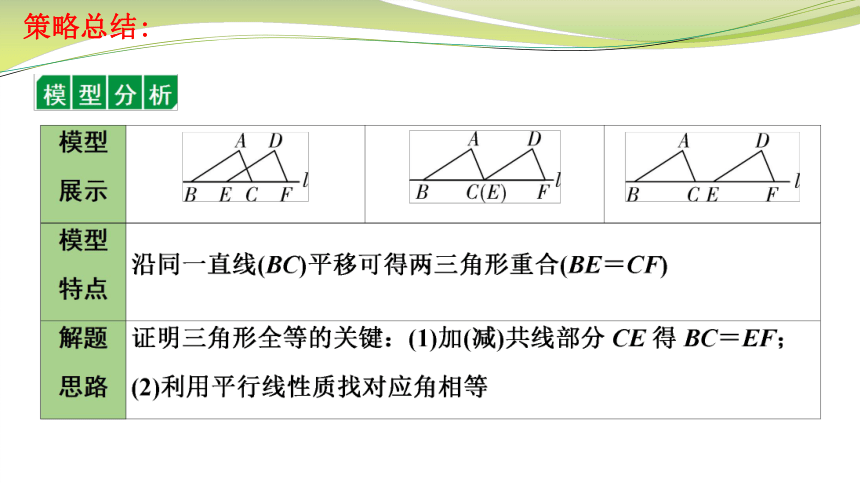
策略总结:
例3 已知:如图,AC、DB相交于点O,AB=DC,∠ABO=∠DCO.
经典例题:
求证:(1)△ABO≌△DCO;
策略总结:
策略总结:
例4 如图,在四边形ABCD中,AD∥BC,AD=BC,过点A作AE⊥AD交BD于点E,过点C作CF⊥BC交BD于点F,求证:△AED≌△CFB.
经典例题:
△AEB≌△CFD;
策略总结:
策略总结:
全等
对应元素:角
边
全等三角形判定
图形变换:平移、旋转、
轴对称
(全等变换)
课堂小练:
第1题图
课堂小练:
第2题图
3.如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
链接中考:
(2019苏州24题8分)
《全等三角形(1)》
基础梳理
性质
判定方法
一般三角形的判定
直角三角形的判定
已知两边对应相等
已知一边和一
角对应相等
已知两角对应相等
判定思路
全等三角形
性质
1. 全等三角形的对应边______,对应角______
2. 全等三角形的周长________,面积______
3. 全等三角形对应的中线、高线、角平分线、中位线都相等
判定方法
类型 图形 判定条件 简写
一般三角形的判定 __________________(基本事实) SSS
__________________________(基本事实) SAS
相等
相等
相等
相等
三边分别相等
两边及其夹角分别
相等
基础梳理
判定方法
类型 图形 判定条件 简写
一般三角形的判定 __________________________(基本事实) ASA
__________________________________ AAS
直角三角形的判定 __________________________ HL
两角及其夹边分别
相等
斜边和一条直角边
分别相等
两角分别相等且其中一组等角的对边相等
基础梳理
判定思路
已知两边对应相等
找夹角→SAS
找第三边→SSS
已知一边和一
角对应相等
边为角的对边→找另一角→AAS
边为角的一边
找夹角的另一边→SAS
找夹边的另一角→ASA
找边的对角→AAS
已知两角
对应相等
找夹边→ASA
找一角的对边→AAS
基础梳理
经典例题:
例1.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=9,BC=5时,线段 AE的长为 ,
(2)已知∠D=35°,∠C=60°,求∠AFD的度数.
4
解:∵△ABC≌△DEB,∠C=60°(已知)
∴∠C=∠DBE=60°,∠A=∠D=35°(全等三角形对应角相等)
∵∠D+∠DBE+∠BED=180°(三角形内角和定理)
∠D=35°(已知)
∴∠ BED=180°-60°-35°=85°(等式性质)
∵ ∠BED+∠AEF=180° (平角定义)
∴ ∠AEF=95°(等式性质)
∴∠AFD=∠AEF+∠A=95°+35°=130°
(三角形一个外角等于与它不相邻的两个内角和)
策略总结:
已知:全等
对应元素:角
边
周长、面积
对应中线、
高线、
角平分线
中位线
……
全等三角形性质
例2 已知△ABC和△DEF,且点B、E、C、F在同一直线上,AB∥DE,AC∥DF,BE=CF.
经典例题:
求证:△ABC≌△DEF
策略总结:
例3 已知:如图,AC、DB相交于点O,AB=DC,∠ABO=∠DCO.
经典例题:
求证:(1)△ABO≌△DCO;
策略总结:
策略总结:
例4 如图,在四边形ABCD中,AD∥BC,AD=BC,过点A作AE⊥AD交BD于点E,过点C作CF⊥BC交BD于点F,求证:△AED≌△CFB.
经典例题:
△AEB≌△CFD;
策略总结:
策略总结:
全等
对应元素:角
边
全等三角形判定
图形变换:平移、旋转、
轴对称
(全等变换)
课堂小练:
第1题图
课堂小练:
第2题图
3.如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
链接中考:
(2019苏州24题8分)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
