河北省元氏县第四中学2022学年-2023学年高二上学期开学考试数学试卷(Word版含答案)
文档属性
| 名称 | 河北省元氏县第四中学2022学年-2023学年高二上学期开学考试数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 10:25:24 | ||
图片预览



文档简介
2022-2023学年度第一学期9月份开学摸底考试
高二数学
一.选择题(共8小题)
1.设i是虚数单位,复数,,则z1 z2在复平面上对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.三棱锥P﹣ABC,PA⊥平面ABC,AB=AC=1,PA=2,∠BAC=120°,则三棱锥P﹣ABC的外接球的半径为( )
A. B. C. D.
3.我国古代数学名著《九章算术》中有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百人,问北乡人数几何?”其意思为:“今有某地北面若干人,西面有7488人,南面有6912人,这三面要征调300人,而北面共征调100人(用分层抽样的方法),则北面共有( )人.”
A.7200 B.8100 C.2496 D.2304
4.已知样本数据2,4,6,a的平均数为4,则该样本的标准差是( )
A. B. C.2 D.
5.已知甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数、众数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的方差变为3.8
C.这五位同学年龄的众数变为19 D.这五位同学年龄的中位数变为19
6.甲投篮球3次,首次投篮命中率为,在投篮过程中,若球被投中,则下次投篮的命中率为,若球未投中,则下次投篮命中率为,则在3次投篮中,恰好投中1次的概率为( )
A. B. C. D.
7.三棱柱ABC﹣DEF中,G为棱AD的中点,若,,,
则=( )
A. B. C. D.
8.若空间四点M、A、B、C共面且,则k的值为( )
A.1 B.2 C.3 D.6
二.多选题(共4小题)
9.已知向量=(2,1),=(﹣3,1),则( )
A. B.与向量共线的单位向量是(,)
C. D.向量在向量上的投影向量是
10.如图,在正方体ABCD﹣A1B1C1D1中,以下四个选项
正确的是( )
A.D1C∥平面A1ABB1 B.A1D1与平面BCD1相交
C.AD⊥平面D1DB D.平面BCD1⊥平面A1ABB1
11.已知甲、乙两个水果店在“十一黄金周”七天的水果销售量统计如图所示.则下列说法正确的是( )
A.甲组数据的极差大于乙组数据的极差
B.甲组数据的平均数大于乙组数据的平均数
C.甲组数据的方差大于乙组数据的方差
D.甲组数据的中位数大于乙组数据的中位数
12.随机地排列数字1,5,6得到一个三位数,则( )
A.可以排成9个不同的三位数 B.所得的三位数是奇数的概率为
C.所得的三位数是偶数的概率为 D.所得的三位数大于400的概率为
三.填空题(共4小题)
13.设复数z=,则下列命题中正确的是 .(填序号)
①|z|=; ②=1﹣i; ③在复平面上对应的点在第一象限;④虚部为2.
14.如图所示,电路原件R1,R2,R3正常工作的概率
分别为,,,则电路能正常工作的概率为 .
15.已知长方体ABCD﹣A1B1C1D1的顶点都在球O的表面上,且AC=AA1=2,则球O的表面积为 .
16.如图,在△ABC中,是BN的中点,
若,则实数m的值是 .
四.解答题(共6小题)
17.已知复数z=(m2﹣m)+(m+3)i,m∈R(i为虚数单位).
(1)当m=2时,求复数z的值;
(2)若复数z在复平面内对应的点位于第二象限,求m的取值范围.
18.在△ABC中,角A,B,C所对的边分别是a,b,c,已知(a+c)(a﹣c)=b(b+c).
(1)求角A的大小;
(2)在下列三个条件中任选一个,补充在下面问题中的横线上,并解答.若b=3,c=4,点D是BC边上的一点,且 ,求线段AD的长.
①AD是△ABC的中线;
②AD是△ABC的角平分线;
③BD=2CD.
19.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,
PA⊥平面ABCD,PA=AD=1,E,F分别是PB,AC
的中点.
(1)证明:EF∥平面PCD;
(2)求三棱锥E﹣ABF的体积.
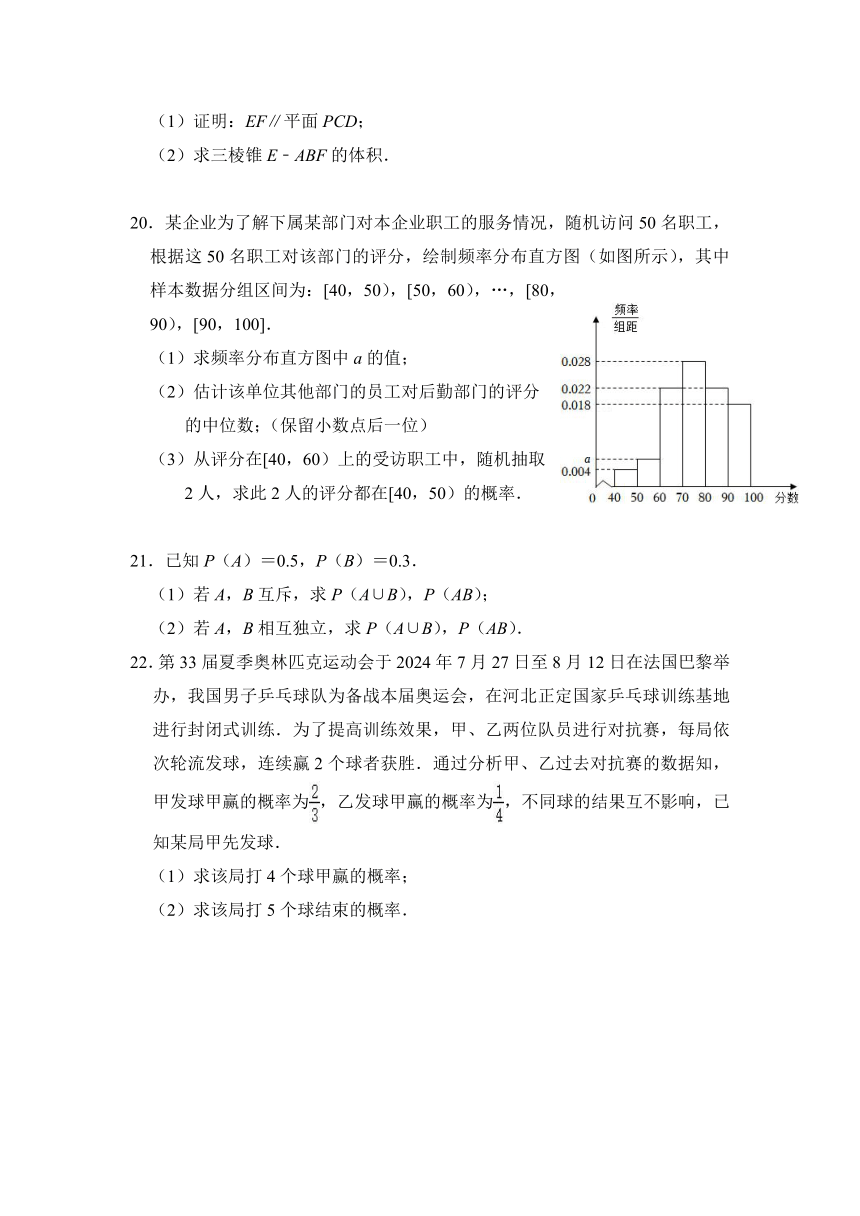
20.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:[40,50),[50,60),…,[80,90),[90,100].
(1)求频率分布直方图中a的值;
(2)估计该单位其他部门的员工对后勤部门的评分
的中位数;(保留小数点后一位)
(3)从评分在[40,60)上的受访职工中,随机抽取
2人,求此2人的评分都在[40,50)的概率.
21.已知P(A)=0.5,P(B)=0.3.
(1)若A,B互斥,求P(A∪B),P(AB);
(2)若A,B相互独立,求P(A∪B),P(AB).
22.第33届夏季奥林匹克运动会于2024年7月27日至8月12日在法国巴黎举办,我国男子乒乓球队为备战本届奥运会,在河北正定国家乒乓球训练基地进行封闭式训练.为了提高训练效果,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢2个球者获胜.通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
(1)求该局打4个球甲赢的概率;
(2)求该局打5个球结束的概率.
参考答案
一.选择题(共8小题)
1. B.
2. A.
3. A.
4. B.
5.B.
6.D.
7.B.
8.D.
二.多选题(共4小题)
(多选)9. AC.
(多选)10.AD.
11.BD.
(多选)12. BD.
三.填空题(共4小题)
13.
故答案为:①②③.
14.
故答案为:.
15.
故答案为:8π.
16.
故答案为:
四.解答题(共6小题)
17.
解:(1)由(a+c)(a﹣c)=b(b+c),得b2+c2﹣a2=﹣bc,
由余弦定理知,,
因为0<A<π,所以.
(2)选①,因为AD是△ABC的中线,
所以=(+),
所以||2=||2+||2+ =,
所以.
选②,因为S△ABC=S△ABD+S△ADC,
所以,
即,
解得.
选③,因为BD=2CD,
所以,
所以
=,
故.
18.
解:(1)当m=2时,z=2+5i,
故.
(2)若复数z在复平面内对应的点位于第二象限,
则,解得0<m<1,
故m的取值范围为(0,1).
19.
解:(1)证明:∵底面ABCD为正方形,F是AC的中点,
∴连接BD,则BD与AC交点即为F点,
∴F也为BD的中点,又E是PB的中点.
∴EF∥PD,又EF 平面PCD,PD 平面PCD,
∴EF∥平面PCD;
(2)∵E,F分别是PB,AC的中点,
∴
=
=,
故三棱锥E﹣ABF的体积为.
20.
解:(1)由题意知,(0.004+a+0.022+0.028+0.022+0.018)×10=1,
解得a=0.006.
(2)由于(0.004+0.006+0.022)×10=0.32,所以中位数为.
(3)由(1)知:50名职工中[40,50)、[50,60)分别有2人、3人,
若[40,50)为职工A、B,[50,60)为职工1、2、3,
所以随机抽取2人的可能组合有{A,B}、{A,1}、{A,2}、{A,3}、{B,1}、{B,2}、{B,3}、{1,2}、{1,3}、{2,3}共10种,
其中2人的评分都在[40,50)有{A,B},即1种,
所以2人的评分都在[40,50)的概率为.
21.
解:(1)P(A)=0.5,P(B)=0.3,
若A,B互斥,P(A∪B)=P(A)+P(B)=0.5+0.3=0.8,
P(AB)=0;
(2)若A,B相互独立,P(A∪B)=P(A)+P(B)﹣P(AB)=0.5+0.3﹣0.5×0.3=0.65,
P(AB)=P(A)P(B)=0.5×0.3=0.15.
22.
解:(1)设甲发球甲赢为事件A,乙发球甲赢为事件B,该局打4个球甲赢为事件C,
由题知,,∴,
∴,
∴该局打4个球甲赢的概率为;
(2)设该局打5个球结束时甲赢为事件D,乙赢为事件E,打5个球结束为事件F,易知D,E为互斥事件,
,
∴
=,
=,
∴,
∴该局打5个球结束的概率为.
高二数学
一.选择题(共8小题)
1.设i是虚数单位,复数,,则z1 z2在复平面上对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.三棱锥P﹣ABC,PA⊥平面ABC,AB=AC=1,PA=2,∠BAC=120°,则三棱锥P﹣ABC的外接球的半径为( )
A. B. C. D.
3.我国古代数学名著《九章算术》中有一抽样问题:“今有北乡若干人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百人,问北乡人数几何?”其意思为:“今有某地北面若干人,西面有7488人,南面有6912人,这三面要征调300人,而北面共征调100人(用分层抽样的方法),则北面共有( )人.”
A.7200 B.8100 C.2496 D.2304
4.已知样本数据2,4,6,a的平均数为4,则该样本的标准差是( )
A. B. C.2 D.
5.已知甲、乙、丙、丁、戊五位同学高一入学时年龄的平均数、中位数、众数均为16,方差为0.8,则三年后,下列判断错误的是( )
A.这五位同学年龄的平均数变为19 B.这五位同学年龄的方差变为3.8
C.这五位同学年龄的众数变为19 D.这五位同学年龄的中位数变为19
6.甲投篮球3次,首次投篮命中率为,在投篮过程中,若球被投中,则下次投篮的命中率为,若球未投中,则下次投篮命中率为,则在3次投篮中,恰好投中1次的概率为( )
A. B. C. D.
7.三棱柱ABC﹣DEF中,G为棱AD的中点,若,,,
则=( )
A. B. C. D.
8.若空间四点M、A、B、C共面且,则k的值为( )
A.1 B.2 C.3 D.6
二.多选题(共4小题)
9.已知向量=(2,1),=(﹣3,1),则( )
A. B.与向量共线的单位向量是(,)
C. D.向量在向量上的投影向量是
10.如图,在正方体ABCD﹣A1B1C1D1中,以下四个选项
正确的是( )
A.D1C∥平面A1ABB1 B.A1D1与平面BCD1相交
C.AD⊥平面D1DB D.平面BCD1⊥平面A1ABB1
11.已知甲、乙两个水果店在“十一黄金周”七天的水果销售量统计如图所示.则下列说法正确的是( )
A.甲组数据的极差大于乙组数据的极差
B.甲组数据的平均数大于乙组数据的平均数
C.甲组数据的方差大于乙组数据的方差
D.甲组数据的中位数大于乙组数据的中位数
12.随机地排列数字1,5,6得到一个三位数,则( )
A.可以排成9个不同的三位数 B.所得的三位数是奇数的概率为
C.所得的三位数是偶数的概率为 D.所得的三位数大于400的概率为
三.填空题(共4小题)
13.设复数z=,则下列命题中正确的是 .(填序号)
①|z|=; ②=1﹣i; ③在复平面上对应的点在第一象限;④虚部为2.
14.如图所示,电路原件R1,R2,R3正常工作的概率
分别为,,,则电路能正常工作的概率为 .
15.已知长方体ABCD﹣A1B1C1D1的顶点都在球O的表面上,且AC=AA1=2,则球O的表面积为 .
16.如图,在△ABC中,是BN的中点,
若,则实数m的值是 .
四.解答题(共6小题)
17.已知复数z=(m2﹣m)+(m+3)i,m∈R(i为虚数单位).
(1)当m=2时,求复数z的值;
(2)若复数z在复平面内对应的点位于第二象限,求m的取值范围.
18.在△ABC中,角A,B,C所对的边分别是a,b,c,已知(a+c)(a﹣c)=b(b+c).
(1)求角A的大小;
(2)在下列三个条件中任选一个,补充在下面问题中的横线上,并解答.若b=3,c=4,点D是BC边上的一点,且 ,求线段AD的长.
①AD是△ABC的中线;
②AD是△ABC的角平分线;
③BD=2CD.
19.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,
PA⊥平面ABCD,PA=AD=1,E,F分别是PB,AC
的中点.
(1)证明:EF∥平面PCD;
(2)求三棱锥E﹣ABF的体积.
20.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:[40,50),[50,60),…,[80,90),[90,100].
(1)求频率分布直方图中a的值;
(2)估计该单位其他部门的员工对后勤部门的评分
的中位数;(保留小数点后一位)
(3)从评分在[40,60)上的受访职工中,随机抽取
2人,求此2人的评分都在[40,50)的概率.
21.已知P(A)=0.5,P(B)=0.3.
(1)若A,B互斥,求P(A∪B),P(AB);
(2)若A,B相互独立,求P(A∪B),P(AB).
22.第33届夏季奥林匹克运动会于2024年7月27日至8月12日在法国巴黎举办,我国男子乒乓球队为备战本届奥运会,在河北正定国家乒乓球训练基地进行封闭式训练.为了提高训练效果,甲、乙两位队员进行对抗赛,每局依次轮流发球,连续赢2个球者获胜.通过分析甲、乙过去对抗赛的数据知,甲发球甲赢的概率为,乙发球甲赢的概率为,不同球的结果互不影响,已知某局甲先发球.
(1)求该局打4个球甲赢的概率;
(2)求该局打5个球结束的概率.
参考答案
一.选择题(共8小题)
1. B.
2. A.
3. A.
4. B.
5.B.
6.D.
7.B.
8.D.
二.多选题(共4小题)
(多选)9. AC.
(多选)10.AD.
11.BD.
(多选)12. BD.
三.填空题(共4小题)
13.
故答案为:①②③.
14.
故答案为:.
15.
故答案为:8π.
16.
故答案为:
四.解答题(共6小题)
17.
解:(1)由(a+c)(a﹣c)=b(b+c),得b2+c2﹣a2=﹣bc,
由余弦定理知,,
因为0<A<π,所以.
(2)选①,因为AD是△ABC的中线,
所以=(+),
所以||2=||2+||2+ =,
所以.
选②,因为S△ABC=S△ABD+S△ADC,
所以,
即,
解得.
选③,因为BD=2CD,
所以,
所以
=,
故.
18.
解:(1)当m=2时,z=2+5i,
故.
(2)若复数z在复平面内对应的点位于第二象限,
则,解得0<m<1,
故m的取值范围为(0,1).
19.
解:(1)证明:∵底面ABCD为正方形,F是AC的中点,
∴连接BD,则BD与AC交点即为F点,
∴F也为BD的中点,又E是PB的中点.
∴EF∥PD,又EF 平面PCD,PD 平面PCD,
∴EF∥平面PCD;
(2)∵E,F分别是PB,AC的中点,
∴
=
=,
故三棱锥E﹣ABF的体积为.
20.
解:(1)由题意知,(0.004+a+0.022+0.028+0.022+0.018)×10=1,
解得a=0.006.
(2)由于(0.004+0.006+0.022)×10=0.32,所以中位数为.
(3)由(1)知:50名职工中[40,50)、[50,60)分别有2人、3人,
若[40,50)为职工A、B,[50,60)为职工1、2、3,
所以随机抽取2人的可能组合有{A,B}、{A,1}、{A,2}、{A,3}、{B,1}、{B,2}、{B,3}、{1,2}、{1,3}、{2,3}共10种,
其中2人的评分都在[40,50)有{A,B},即1种,
所以2人的评分都在[40,50)的概率为.
21.
解:(1)P(A)=0.5,P(B)=0.3,
若A,B互斥,P(A∪B)=P(A)+P(B)=0.5+0.3=0.8,
P(AB)=0;
(2)若A,B相互独立,P(A∪B)=P(A)+P(B)﹣P(AB)=0.5+0.3﹣0.5×0.3=0.65,
P(AB)=P(A)P(B)=0.5×0.3=0.15.
22.
解:(1)设甲发球甲赢为事件A,乙发球甲赢为事件B,该局打4个球甲赢为事件C,
由题知,,∴,
∴,
∴该局打4个球甲赢的概率为;
(2)设该局打5个球结束时甲赢为事件D,乙赢为事件E,打5个球结束为事件F,易知D,E为互斥事件,
,
∴
=,
=,
∴,
∴该局打5个球结束的概率为.
同课章节目录
