11.1.2 三角形的高、中线与角平分线 课件(38页PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线 课件(38页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 21:45:17 | ||
图片预览




文档简介
(共40张PPT)
11.1.2三角形的高、中线
与角平分线
人教版八年级上册
第十一章 三角形
教学目标
1.三角形的高、中线与角平分线的概念。
2.三角形的高、中线与角平分线的画法。
新知导入
课前回顾
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
把一条线段分成两条相等的线段的点。
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
新知导入
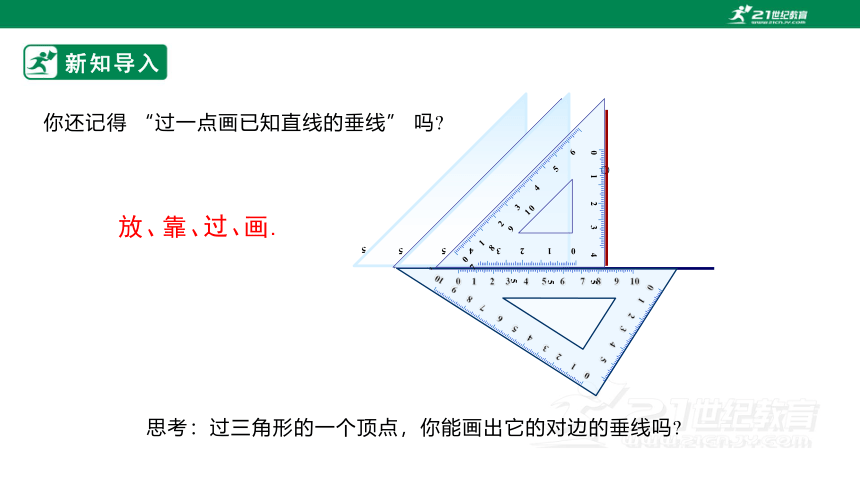
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
新知讲解
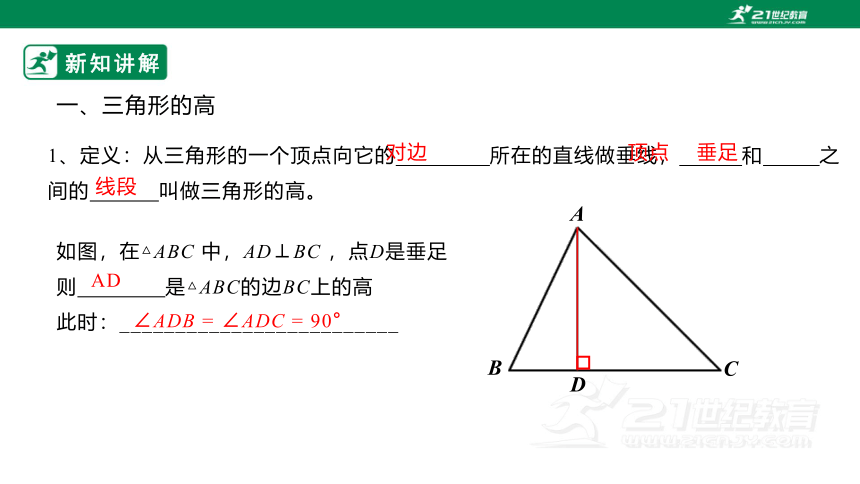
一、三角形的高
1、定义:从三角形的一个顶点向它的 所在的直线做垂线, 和 之
间的 叫做三角形的高。
如图,在△ABC 中,AD⊥BC ,点D是垂足
则 是△ABC的边BC上的高
此时:_________________________
A
B
C
D
对边
顶点
垂足
线段
AD
∠ADB = ∠ADC = 90°
新知讲解
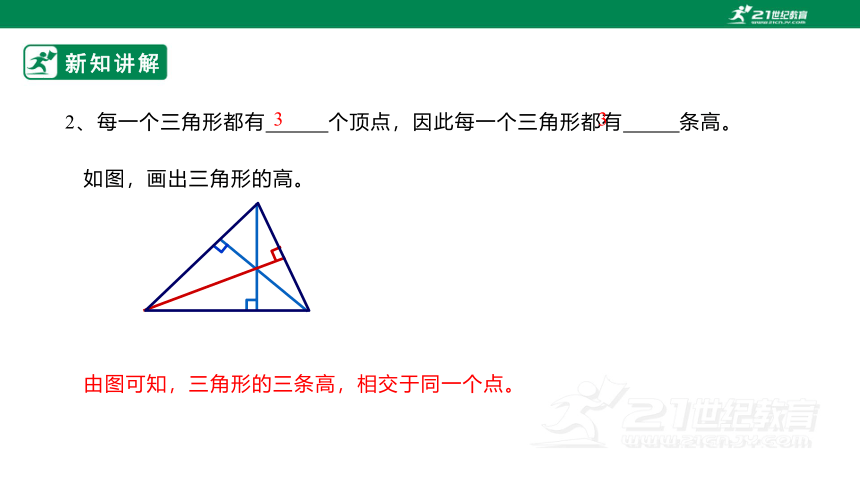
2、每一个三角形都有 个顶点,因此每一个三角形都有 条高。
如图,画出三角形的高。
由图可知,三角形的三条高,相交于同一个点。
3
3
新知讲解
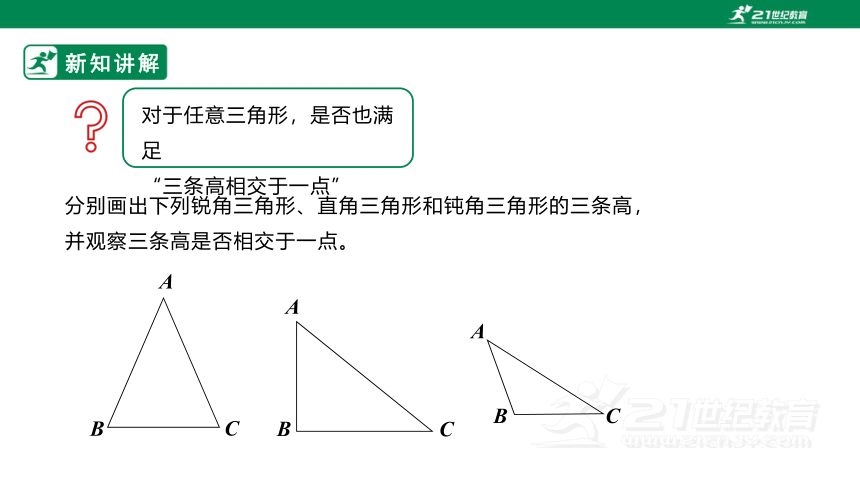
对于任意三角形,是否也满足
“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点。
A
C
B
A
C
B
A
C
B
新知讲解
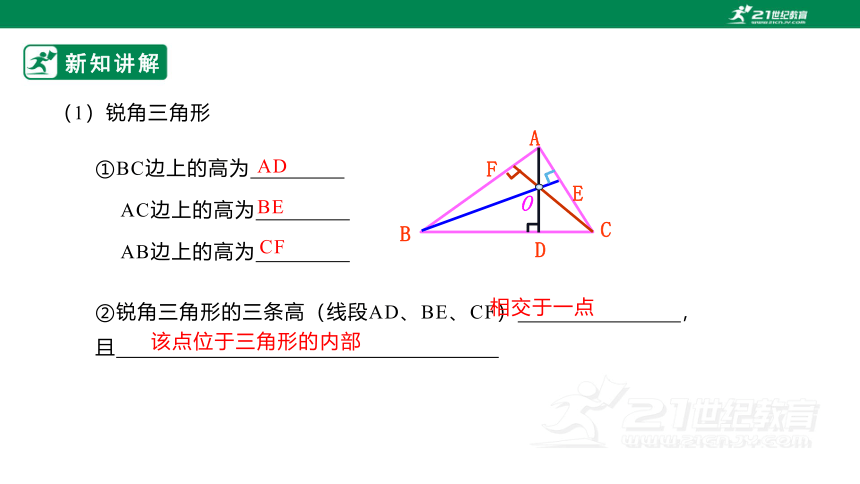
(1)锐角三角形
O
A
B
C
D
E
F
①BC边上的高为
AC边上的高为
AB边上的高为
AD
BE
CF
②锐角三角形的三条高(线段AD、BE、CF) ,
且
相交于一点
该点位于三角形的内部
新知讲解
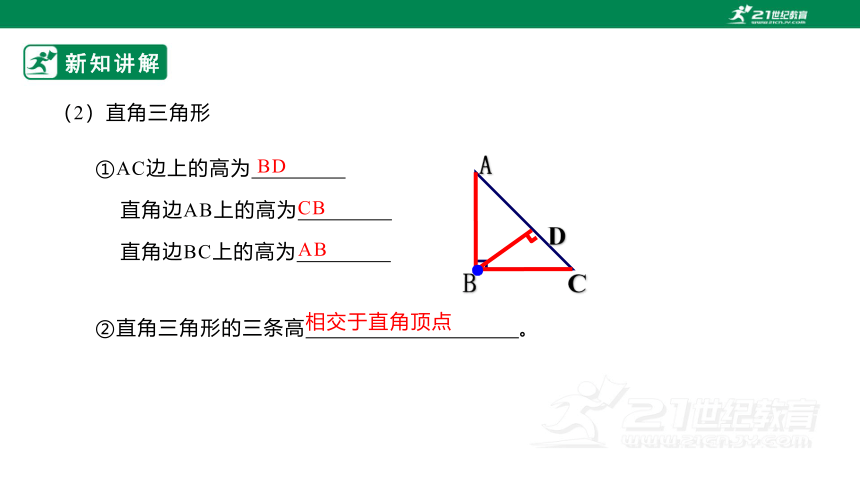
(2)直角三角形
A
B
C
D
●
①AC边上的高为
直角边AB上的高为
直角边BC上的高为
BD
CB
AB
②直角三角形的三条高 。
相交于直角顶点
新知讲解
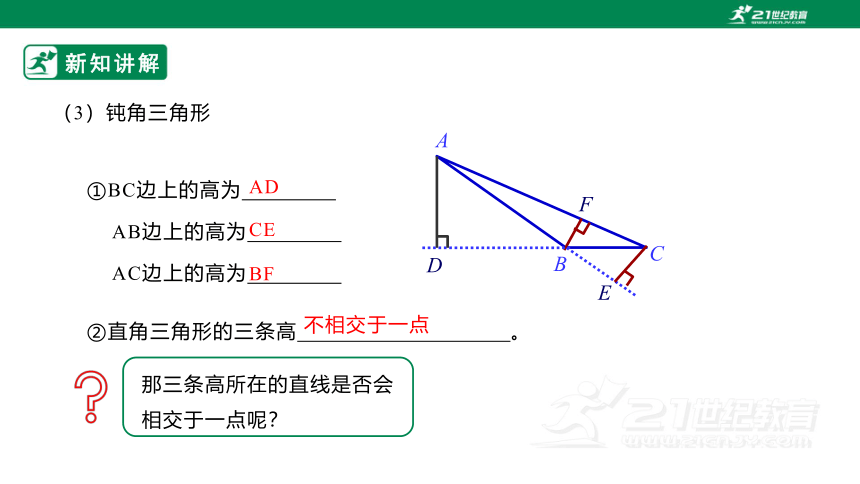
(3)钝角三角形
A
B
C
D
E
F
①BC边上的高为
AB边上的高为
AC边上的高为
AD
CE
BF
②直角三角形的三条高 。
不相交于一点
那三条高所在的直线是否会相交于一点呢?
新知讲解
A
B
C
D
F
O
E
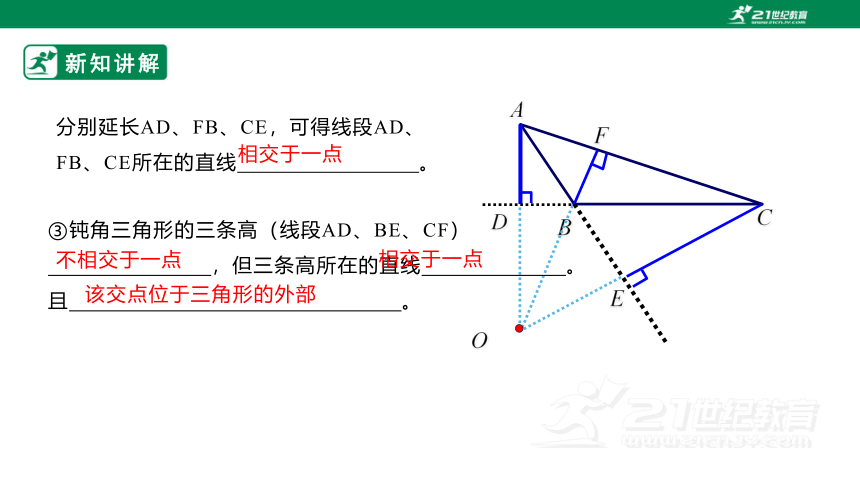
分别延长AD、FB、CE,可得线段AD、
FB、CE所在的直线 。
相交于一点
③钝角三角形的三条高(线段AD、BE、CF)
,但三条高所在的直线 。
且 。
不相交于一点
相交于一点
该交点位于三角形的外部
新知讲解
教 师 点 拨
(1)每一个三角形中都含有 条高,且三条高所在的直线 。
(2)锐角三角形的三条高线相交于三角形的 。
(3)直角三角形的三条高线相交于三角形的 。
(4)钝角三角形的三条高线相交于三角形的 。
3
相交于一点
内部
直角顶点
外部
新知讲解
二、三角形的中线
1、定义:在三角形中,连接一个 与它 的 线段,叫做这个三角形的中线。
顶点
对边中点
如图,在△ABC 中,E是BC的中点
则 是BC边上的中线,
此时:______________________
B
A
C
A
E
AE
BE=CE
如图,在△ABC 中,AE是BC边上的中线
则E是BC的 ,
此时:______________________
中点
BE=CE
新知讲解
2、每一个三角形都有 个顶点,因此每一个三角形都有 条中线。
3
3
如图,画出三角形的中线
由图可知,三角形的三条中线,相交于同一个点。
新知讲解
对于任意三角形,是否也满足
“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点。
A
C
B
A
C
B
A
C
B
新知讲解
教师总结
三角形的三条中线 ,且 。
相交于一点
该交点位于三角形内部
三角形三条中线的交点,叫做三角形的的 。
重心
新知讲解
三、三角形的角平分线
1、定义:在三角形中,一个内角的 与它的 相交,这个角的
与 之间的线段,叫做三角形的角平分线。
平分线
对边
顶点
交点
如图,在△ABC 中,∠1=∠2
则 是∠A的角平分线
1
2
A
B
C
D
AD
如图,在△ABC 中,AD是∠A的角平分线
则___________
∠1=∠2
新知讲解
2、每一个三角形都有 个内角,因此每一个三角形都有 条角平分线。
3
3
如图,画出下列三角形的中线
新知讲解
教师总结
三角形的三条角平分线 ,且 。
相交于一点
该交点位于三角形内部
三角形的角平分线是一条 。
线段
课堂练习
1、(2022春 泗县期中)如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
A.AD是△ABE的角平分线
B.BE是△ABD边AD上的中线
C.CH为△ACD边AD上的高
D.AH为△ABC的角平分线
【解析】A、根据三角形的角平分线的概念,知AG是△ABE的角平分线,故本选项错误;
B、根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故本选项错误;
C、根据三角形的高的概念,知CH为△ACD的边AD上的高,故本选项正确;
D、根据三角形的角平分线的概念,知AD是△ABC的角平分线,故本选项错误.
C
课堂练习
2、(2022春 亭湖区校级期中)如图,CM是△ABC的中线,AB=10cm,则BM的长为( )
A.7cm B.6cm
C.5cm D.4cm
【解析】∵CM是△ABC的中线,AB=10cm
∴BM= AB=5cm
故答案选C
C
课堂练习
3、(2021秋 富裕县期末)如图,在△ABC中,AC边上的高是( )
A.线段AD
B.线段BE
C.线段BF
D.线段CF
【解析】∵点B到AC边的垂线段是BE
∴AC边上的高是BE
故答案选B
B
课堂练习
4、(2021秋 高青县期末)如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;
②∠AFG=∠AGF;
③∠FAG=2∠ACF;
④AF=FB.
A.①②③④ B.①②④ C.①②③ D.③④
课堂练习
【解析】∵BE是△ABC的中线,
∴AE=CE,
∴△ABE的面积等于△BCE的面积,故①正确;
∵AD是△ABC的高线,
∴∠ADC=90°,
∴∠ABC+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABC=∠CAD,
∵CF为△ABC的角平分线,
∴∠ACF=∠BCF= ∠ACB,
∵∠AFC=∠ABC+∠BCF,∠AGF=∠ACF+∠CAD,
∴∠AFC=∠AGF=∠AFG,
故②正确;
∵∠BAD+∠CAD=∠ACB+∠CAD=90°,
∴∠BAD=∠ACD,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件无法证明AF=FB,故④错误
综上,故答案选C。
课堂练习
5、(2021春 嵩县期末)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 。
【解析】∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差
=(AB+BD+AD)-(BC+BD+CD)
=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2
2
课堂练习
6、(2020秋 虹口区校级月考)如图,在△ABC中,AB>AC,BC边上的高AD和中线AE及∠BAC的平分线AF将∠BAC四等分,则∠EAD= 。
【解析】∵AD⊥BC
∴∠ADC=∠ADF=90°
又∠FAD=∠CAD,AD=AD
∴△ADC≌△ADF(ASA)
∴AF=AC,FD=DC
∵∠BAE=∠FAE
∴
∵AF平分∠BAC
∴
∴
∴
∴ =
∴
∴FC2=2EF2
又FC=2FD
∴EF2=2FD2
即
∵∠EAF=∠ DAF
∴
∴
在Rt△AFD中
DE2=AE2﹣AD2=2AD2﹣AD2=AD2
∵DE=AD
∴△ADF是等腰直角三角形
∴∠EAD=45°
45°
课堂练习
7、(2021秋 无棣县期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 。
【解析】如图
∵BD=3,CD=1
∴BC=BD﹣CD=2
又∵AD是BC边上的高,AD=2
∴△ABC的面积= BC AD= ×2×2=2
2
课堂练习
8、如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长。
【解析】如图,过点A作BC边上的高线AE,交CB延长线于点E
∵ BC AE= AC BD,AC=8,BC=4,高BD=3
∴ ×4AE= ×8×3
解得 AE=6
∴AE的长为6
课堂练习
9、如图,AD为△ABC的中线,AB=12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC<AB)。
【解析】∵AD为△ABC的中线
∴BD=CD
∵△ABD和△ADC的周长差是4cm
∴AB+AD+BD﹣(AC+AD+CD)
=AB+AD+BD﹣AC﹣AD﹣BD
=AB﹣AC
=4cm
∵AB=12cm
∴AC=AB﹣4cm=8cm
∴△ABC的边AC的长为8cm
课堂总结
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
作业布置
1、(2021秋 江油市期末)有两条高在三角形外部的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
【解析】有两条高在三角形外部的是钝角三角形,故答案选C。
C
作业布置
2、(2020春 奉贤区期末)如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,有下列说法:
①点A与点B的距离是线段AB的长; ②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高; ④线段CD是△BCD边BD上的高。
上述说法中,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【解析】①、根据两点间的距离的定义得出:点A与点B的距离是线段AB的长,∴①正确;
②、点A到直线CD的距离是线段AD的长,∴②正确;
③、根据三角形的高的定义,△ABC边AB上的高是线段CD,∴③正确;
④、根据三角形的高的定义,△DBC边BD上的高是线段CD,∴④正确。
综上所述,正确的是①②③④共4个,故答案选D。
D
作业布置
3、(2021秋 越秀区校级期中)如图,在△ABC中,AD是边BC上的中线,△ABD的周长比△ADC的周长多3,AB与AC的和为13,则AB的长为 。
【解析】∵AD是BC边上的中线
∴BD=CD
∴△ABD的周长﹣△ADC的周长
=(AB+AD+BD)﹣(AC+AD+CD)
=AB﹣AC
=3
即AB﹣AC=3①
又AB+AC=13②
①+②得2AB=16
解得 AB=8
8
作业布置
4、(2020秋 仓山区期中)如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则 =_______。
【解析】∵△ABC中,AD为中线
∴BD=DC
∴S△ABD=S△ADC
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=4
∴ AB ED= AC DF
∴ ×6×ED= ×4×DF
∴
作业布置
5、(2020春 海淀区校级期末)已知BD是△ABC的中线,AB=7,BC=3,且△ABD的周长为15,则△BCD的周长为 。
【解析】∵BD是△ABC的中线
∴AD=CD
∵△ABD的周长为15,AB=7,BC=3
∴△BCD的周长是15﹣(7﹣3)=11
11
作业布置
6、(2021秋 河口县期末)如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长。
【解析】∵DB为△ABC的中线
∴AD=CD
设AD=CD=x,则AB=2x
当x+2x=12,解得x=4
BC+x=15,解得BC=11
此时△ABC的三边长为:AB=AC=8,BC=11
当x+2x=15,BC+x=12,解得x=5,BC=7
此时△ABC的三边长为:AB=AC=10,BC=7
作业布置
7、(2020秋 饶平县校级期末)如图,△ABC中,AD是高,
AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,
求∠DAE和∠BOA的度数。
【解析】∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°
又∵AD是高
∴∠ADC=90°
∴∠DAC=180°﹣90°﹣∠C=30°
∵AE、BF是角平分线
∴∠CBF=∠ABF=35°,∠EAF=25°
∴∠DAE=∠DAC﹣∠EAF=5°
∠AFB=∠C+∠CBF=60°+35°=95°
∴∠BOA=∠EAF+∠AFB=25°+95°=120°
∴∠DAC=30°,∠BOA=120°
∴∠DAE=5°,∠BOA=120°
作业布置
8、(2020秋 乐陵市期中)如图,在△ABC中∠B=30°,∠ACB=110°,AD是BC边上高线,AE平分∠BAC,求∠DAE的度数。
【解析】∵∠B=30°,∠ACB=110°
∴∠BAC=180°﹣30°﹣110°=40°
∵AE平分∠BAC
∴∠BAE= ∠BAC= ×40°=20°
∵∠B=30°,AD是BC边上高线
∴∠BAD=90°﹣30°=60°
∴∠DAE=∠BAD﹣∠BAE=60°﹣20°=40°
∴∠DAE的度数为40°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.1.2三角形的高、中线
与角平分线
人教版八年级上册
第十一章 三角形
教学目标
1.三角形的高、中线与角平分线的概念。
2.三角形的高、中线与角平分线的画法。
新知导入
课前回顾
垂线
线段中点
角平分线
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
把一条线段分成两条相等的线段的点。
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
新知导入
你还记得 “过一点画已知直线的垂线” 吗
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
思考:过三角形的一个顶点,你能画出它的对边的垂线吗
新知讲解
一、三角形的高
1、定义:从三角形的一个顶点向它的 所在的直线做垂线, 和 之
间的 叫做三角形的高。
如图,在△ABC 中,AD⊥BC ,点D是垂足
则 是△ABC的边BC上的高
此时:_________________________
A
B
C
D
对边
顶点
垂足
线段
AD
∠ADB = ∠ADC = 90°
新知讲解
2、每一个三角形都有 个顶点,因此每一个三角形都有 条高。
如图,画出三角形的高。
由图可知,三角形的三条高,相交于同一个点。
3
3
新知讲解
对于任意三角形,是否也满足
“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点。
A
C
B
A
C
B
A
C
B
新知讲解
(1)锐角三角形
O
A
B
C
D
E
F
①BC边上的高为
AC边上的高为
AB边上的高为
AD
BE
CF
②锐角三角形的三条高(线段AD、BE、CF) ,
且
相交于一点
该点位于三角形的内部
新知讲解
(2)直角三角形
A
B
C
D
●
①AC边上的高为
直角边AB上的高为
直角边BC上的高为
BD
CB
AB
②直角三角形的三条高 。
相交于直角顶点
新知讲解
(3)钝角三角形
A
B
C
D
E
F
①BC边上的高为
AB边上的高为
AC边上的高为
AD
CE
BF
②直角三角形的三条高 。
不相交于一点
那三条高所在的直线是否会相交于一点呢?
新知讲解
A
B
C
D
F
O
E
分别延长AD、FB、CE,可得线段AD、
FB、CE所在的直线 。
相交于一点
③钝角三角形的三条高(线段AD、BE、CF)
,但三条高所在的直线 。
且 。
不相交于一点
相交于一点
该交点位于三角形的外部
新知讲解
教 师 点 拨
(1)每一个三角形中都含有 条高,且三条高所在的直线 。
(2)锐角三角形的三条高线相交于三角形的 。
(3)直角三角形的三条高线相交于三角形的 。
(4)钝角三角形的三条高线相交于三角形的 。
3
相交于一点
内部
直角顶点
外部
新知讲解
二、三角形的中线
1、定义:在三角形中,连接一个 与它 的 线段,叫做这个三角形的中线。
顶点
对边中点
如图,在△ABC 中,E是BC的中点
则 是BC边上的中线,
此时:______________________
B
A
C
A
E
AE
BE=CE
如图,在△ABC 中,AE是BC边上的中线
则E是BC的 ,
此时:______________________
中点
BE=CE
新知讲解
2、每一个三角形都有 个顶点,因此每一个三角形都有 条中线。
3
3
如图,画出三角形的中线
由图可知,三角形的三条中线,相交于同一个点。
新知讲解
对于任意三角形,是否也满足
“三条高相交于一点”
分别画出下列锐角三角形、直角三角形和钝角三角形的三条高,
并观察三条高是否相交于一点。
A
C
B
A
C
B
A
C
B
新知讲解
教师总结
三角形的三条中线 ,且 。
相交于一点
该交点位于三角形内部
三角形三条中线的交点,叫做三角形的的 。
重心
新知讲解
三、三角形的角平分线
1、定义:在三角形中,一个内角的 与它的 相交,这个角的
与 之间的线段,叫做三角形的角平分线。
平分线
对边
顶点
交点
如图,在△ABC 中,∠1=∠2
则 是∠A的角平分线
1
2
A
B
C
D
AD
如图,在△ABC 中,AD是∠A的角平分线
则___________
∠1=∠2
新知讲解
2、每一个三角形都有 个内角,因此每一个三角形都有 条角平分线。
3
3
如图,画出下列三角形的中线
新知讲解
教师总结
三角形的三条角平分线 ,且 。
相交于一点
该交点位于三角形内部
三角形的角平分线是一条 。
线段
课堂练习
1、(2022春 泗县期中)如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
A.AD是△ABE的角平分线
B.BE是△ABD边AD上的中线
C.CH为△ACD边AD上的高
D.AH为△ABC的角平分线
【解析】A、根据三角形的角平分线的概念,知AG是△ABE的角平分线,故本选项错误;
B、根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故本选项错误;
C、根据三角形的高的概念,知CH为△ACD的边AD上的高,故本选项正确;
D、根据三角形的角平分线的概念,知AD是△ABC的角平分线,故本选项错误.
C
课堂练习
2、(2022春 亭湖区校级期中)如图,CM是△ABC的中线,AB=10cm,则BM的长为( )
A.7cm B.6cm
C.5cm D.4cm
【解析】∵CM是△ABC的中线,AB=10cm
∴BM= AB=5cm
故答案选C
C
课堂练习
3、(2021秋 富裕县期末)如图,在△ABC中,AC边上的高是( )
A.线段AD
B.线段BE
C.线段BF
D.线段CF
【解析】∵点B到AC边的垂线段是BE
∴AC边上的高是BE
故答案选B
B
课堂练习
4、(2021秋 高青县期末)如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;
②∠AFG=∠AGF;
③∠FAG=2∠ACF;
④AF=FB.
A.①②③④ B.①②④ C.①②③ D.③④
课堂练习
【解析】∵BE是△ABC的中线,
∴AE=CE,
∴△ABE的面积等于△BCE的面积,故①正确;
∵AD是△ABC的高线,
∴∠ADC=90°,
∴∠ABC+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∴∠ABC=∠CAD,
∵CF为△ABC的角平分线,
∴∠ACF=∠BCF= ∠ACB,
∵∠AFC=∠ABC+∠BCF,∠AGF=∠ACF+∠CAD,
∴∠AFC=∠AGF=∠AFG,
故②正确;
∵∠BAD+∠CAD=∠ACB+∠CAD=90°,
∴∠BAD=∠ACD,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件无法证明AF=FB,故④错误
综上,故答案选C。
课堂练习
5、(2021春 嵩县期末)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 。
【解析】∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差
=(AB+BD+AD)-(BC+BD+CD)
=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2
2
课堂练习
6、(2020秋 虹口区校级月考)如图,在△ABC中,AB>AC,BC边上的高AD和中线AE及∠BAC的平分线AF将∠BAC四等分,则∠EAD= 。
【解析】∵AD⊥BC
∴∠ADC=∠ADF=90°
又∠FAD=∠CAD,AD=AD
∴△ADC≌△ADF(ASA)
∴AF=AC,FD=DC
∵∠BAE=∠FAE
∴
∵AF平分∠BAC
∴
∴
∴
∴ =
∴
∴FC2=2EF2
又FC=2FD
∴EF2=2FD2
即
∵∠EAF=∠ DAF
∴
∴
在Rt△AFD中
DE2=AE2﹣AD2=2AD2﹣AD2=AD2
∵DE=AD
∴△ADF是等腰直角三角形
∴∠EAD=45°
45°
课堂练习
7、(2021秋 无棣县期中)若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 。
【解析】如图
∵BD=3,CD=1
∴BC=BD﹣CD=2
又∵AD是BC边上的高,AD=2
∴△ABC的面积= BC AD= ×2×2=2
2
课堂练习
8、如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长。
【解析】如图,过点A作BC边上的高线AE,交CB延长线于点E
∵ BC AE= AC BD,AC=8,BC=4,高BD=3
∴ ×4AE= ×8×3
解得 AE=6
∴AE的长为6
课堂练习
9、如图,AD为△ABC的中线,AB=12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC<AB)。
【解析】∵AD为△ABC的中线
∴BD=CD
∵△ABD和△ADC的周长差是4cm
∴AB+AD+BD﹣(AC+AD+CD)
=AB+AD+BD﹣AC﹣AD﹣BD
=AB﹣AC
=4cm
∵AB=12cm
∴AC=AB﹣4cm=8cm
∴△ABC的边AC的长为8cm
课堂总结
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°
∵ AD是△ABC的BC上的中线
∴ BD=CD= BC
∵AD是△ABC的∠BAC的平分线
∴ ∠1=∠2= ∠BAC
作业布置
1、(2021秋 江油市期末)有两条高在三角形外部的三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
【解析】有两条高在三角形外部的是钝角三角形,故答案选C。
C
作业布置
2、(2020春 奉贤区期末)如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,有下列说法:
①点A与点B的距离是线段AB的长; ②点A到直线CD的距离是线段AD的长;
③线段CD是△ABC边AB上的高; ④线段CD是△BCD边BD上的高。
上述说法中,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【解析】①、根据两点间的距离的定义得出:点A与点B的距离是线段AB的长,∴①正确;
②、点A到直线CD的距离是线段AD的长,∴②正确;
③、根据三角形的高的定义,△ABC边AB上的高是线段CD,∴③正确;
④、根据三角形的高的定义,△DBC边BD上的高是线段CD,∴④正确。
综上所述,正确的是①②③④共4个,故答案选D。
D
作业布置
3、(2021秋 越秀区校级期中)如图,在△ABC中,AD是边BC上的中线,△ABD的周长比△ADC的周长多3,AB与AC的和为13,则AB的长为 。
【解析】∵AD是BC边上的中线
∴BD=CD
∴△ABD的周长﹣△ADC的周长
=(AB+AD+BD)﹣(AC+AD+CD)
=AB﹣AC
=3
即AB﹣AC=3①
又AB+AC=13②
①+②得2AB=16
解得 AB=8
8
作业布置
4、(2020秋 仓山区期中)如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则 =_______。
【解析】∵△ABC中,AD为中线
∴BD=DC
∴S△ABD=S△ADC
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=4
∴ AB ED= AC DF
∴ ×6×ED= ×4×DF
∴
作业布置
5、(2020春 海淀区校级期末)已知BD是△ABC的中线,AB=7,BC=3,且△ABD的周长为15,则△BCD的周长为 。
【解析】∵BD是△ABC的中线
∴AD=CD
∵△ABD的周长为15,AB=7,BC=3
∴△BCD的周长是15﹣(7﹣3)=11
11
作业布置
6、(2021秋 河口县期末)如图,在△ABC中,AB=AC,DB为△ABC的中线,且BD将△ABC周长分为12cm与15cm两部分,求三角形各边长。
【解析】∵DB为△ABC的中线
∴AD=CD
设AD=CD=x,则AB=2x
当x+2x=12,解得x=4
BC+x=15,解得BC=11
此时△ABC的三边长为:AB=AC=8,BC=11
当x+2x=15,BC+x=12,解得x=5,BC=7
此时△ABC的三边长为:AB=AC=10,BC=7
作业布置
7、(2020秋 饶平县校级期末)如图,△ABC中,AD是高,
AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,
求∠DAE和∠BOA的度数。
【解析】∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°
又∵AD是高
∴∠ADC=90°
∴∠DAC=180°﹣90°﹣∠C=30°
∵AE、BF是角平分线
∴∠CBF=∠ABF=35°,∠EAF=25°
∴∠DAE=∠DAC﹣∠EAF=5°
∠AFB=∠C+∠CBF=60°+35°=95°
∴∠BOA=∠EAF+∠AFB=25°+95°=120°
∴∠DAC=30°,∠BOA=120°
∴∠DAE=5°,∠BOA=120°
作业布置
8、(2020秋 乐陵市期中)如图,在△ABC中∠B=30°,∠ACB=110°,AD是BC边上高线,AE平分∠BAC,求∠DAE的度数。
【解析】∵∠B=30°,∠ACB=110°
∴∠BAC=180°﹣30°﹣110°=40°
∵AE平分∠BAC
∴∠BAE= ∠BAC= ×40°=20°
∵∠B=30°,AD是BC边上高线
∴∠BAD=90°﹣30°=60°
∴∠DAE=∠BAD﹣∠BAE=60°﹣20°=40°
∴∠DAE的度数为40°
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
