人教版九年级数学上册 第23章《旋转》单元测试题(word,含答案)
文档属性
| 名称 | 人教版九年级数学上册 第23章《旋转》单元测试题(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 10:38:25 | ||
图片预览

文档简介
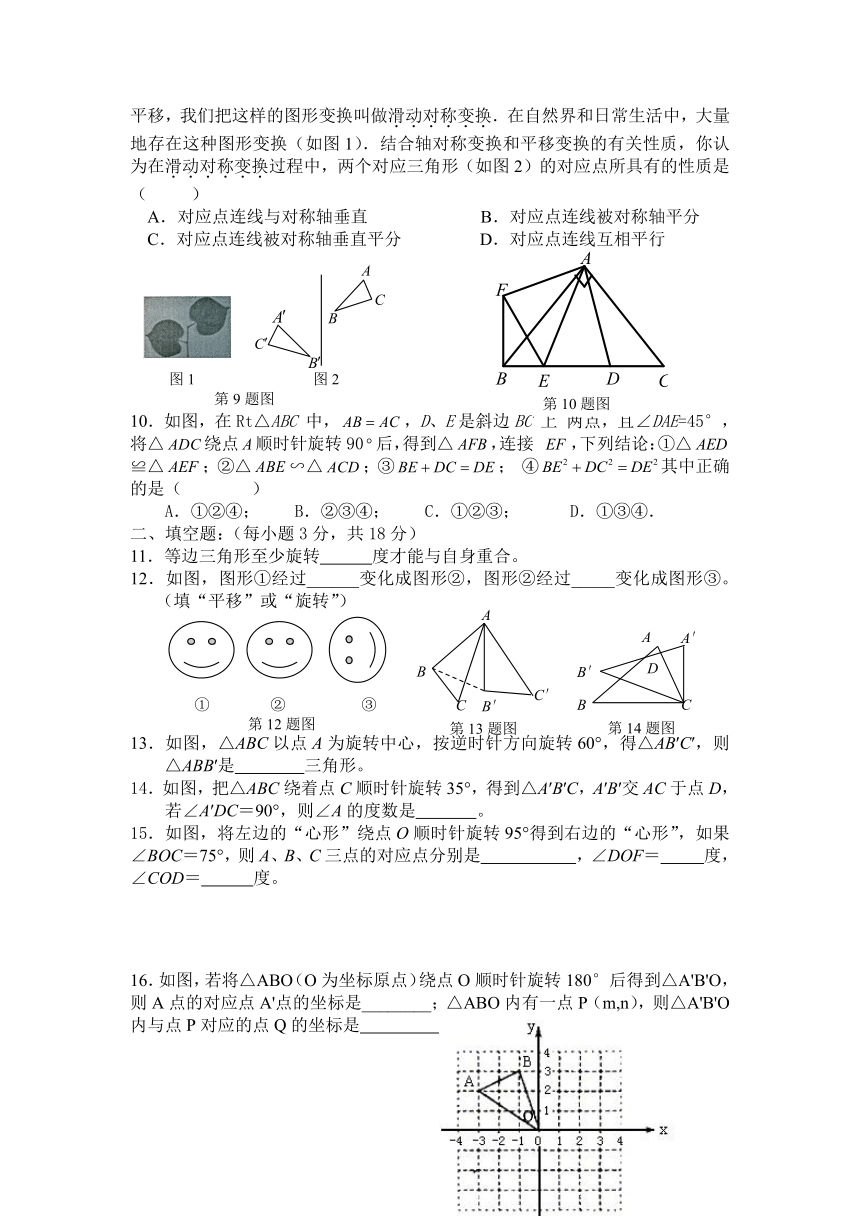
2022学年人教版九年级数学上册第二十三章《旋转》单元测试题
(时间90分钟,满分100分)
一、选择题:(每小题3分,共30分)
1.下面的图形中,是中心对称图形的是( )
A. B. C. D.
2.如图可以看作正△OAB绕点O通过( )旋转所得到的
A.3次 B.4次 C.5次 D.6次
3.下列运动是属于旋转的是( )
A.滚动过程中的篮球的滚动 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折过程
4.将图形1按顺时针方向旋转90°后的图形是( )
A B C D
5.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
6.如图,该图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.90° D.120°
7.在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
8.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
A.10° B.15° C.20° D.25°
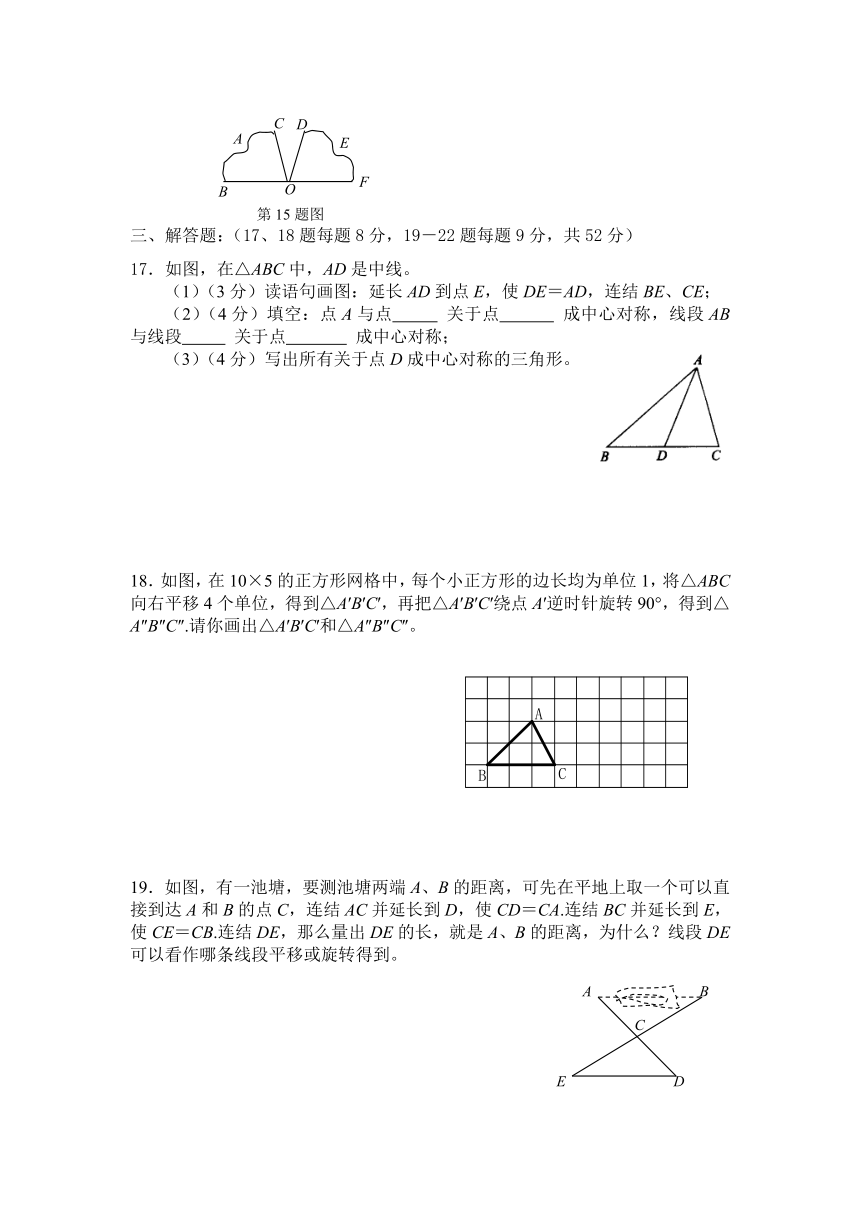
9.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
10.如图,在Rt△ABC 中,,D、E是斜边BC 上 两点,且∠DAE=45°,将△绕点顺时针旋转90后,得到△,连接 ,下列结论:①△≌△;②△∽△;③; ④其中正确的是( )
A.①②④; B.②③④; C.①②③; D.①③④.
二、填空题:(每小题3分,共18分)
11.等边三角形至少旋转 度才能与自身重合。
12.如图,图形①经过______变化成图形②,图形②经过_____变化成图形③。(填“平移”或“旋转”)
13.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则△ABB′是 三角形。
14.如图,把△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是 。
15.如图,将左边的“心形”绕点O顺时针旋转95°得到右边的“心形”,如果∠BOC=75°,则A、B、C三点的对应点分别是 ,∠DOF= 度,∠COD= 度。
16.如图,若将△ABO(O为坐标原点)绕点O顺时针旋转180°后得到△A'B'O,则A点的对应点A'点的坐标是________;△ABO内有一点P(m,n),则△A'B'O内与点P对应的点Q的坐标是 。
三、解答题:(17、18题每题8分,19-22题每题9分,共52分)
17.如图,在△ABC中,AD是中线。
(1)(3分)读语句画图:延长AD到点E,使DE=AD,连结BE、CE;
(2)(4分)填空:点A与点 关于点 成中心对称,线段AB与线段 关于点 成中心对称;
(3)(4分)写出所有关于点D成中心对称的三角形。
18.如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″.请你画出△A′B′C′和△A″B″C″。
19.如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使CE=CB.连结DE,那么量出DE的长,就是A、B的距离,为什么?线段DE可以看作哪条线段平移或旋转得到。
20、如图,已知:
(1) AC的长等于_______.
(2)将向右平移2个单位得到,写出点的对应点的坐标;
(3) 将绕点按顺时针方向旋转后得到A1B1C1,写出A点对应点A1的坐标.
21.如图,已知四边形为正方形,经过旋转后能与重合.
(1)指出旋转的中心和旋转的方向、角度;
(2)若,求的长。
22.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
答案:
九年级数学第二十三章《旋转》单元测试题
1.D 2.C 3.B 4.C 5.B 6.C 7.B 8.B 9.B 10.D
11.120 12.平移,旋转 13.等边 14.55° 15.E、D、F,75,20 16.(3,-2),(-m,-n)
17.解:(1)如图:
(2)E,D,EC,D
(3)△ABD与△ECD;
△ACD与△EBD;
△ABE与△ECA;
△ABC与△ECB.
18.如图:
19.解:因为AC=CD,CE=CB,∠ACB=∠DCE
所以△ACB≌△DCE
所以DE=AB
DE可看作AB绕点C旋转180°得到。
20.(1).(2)(1,2).(3)(3,0).
21.解:(1)△BCE绕点B逆时针旋转90°可与△BAF重合;
(2)Rt△BCE中,BC=4,CE=3,由勾股定理得:BE=5,
由旋转知,BF=BE=5,∠EBF=90°,
由勾股定理得: EF=.
22.解:(1)不正确。若旋转至点F落在AB上时,
BF<AB,而DF>AD,即DF>AB,
则此时DF>BF.
(2)DG=BE.如图2,连接BE.
在正方形ABCD和正方形AEFG中,
AB=AD,AE=AG,∠DAB=∠GAE=90°,
所以∠DAG=∠BAE,所以△ABE≌△ADG,
所以DG=BE.
(时间90分钟,满分100分)
一、选择题:(每小题3分,共30分)
1.下面的图形中,是中心对称图形的是( )
A. B. C. D.
2.如图可以看作正△OAB绕点O通过( )旋转所得到的
A.3次 B.4次 C.5次 D.6次
3.下列运动是属于旋转的是( )
A.滚动过程中的篮球的滚动 B.钟表的钟摆的摆动
C.气球升空的运动 D.一个图形沿某直线对折过程
4.将图形1按顺时针方向旋转90°后的图形是( )
A B C D
5.如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )
6.如图,该图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.90° D.120°
7.在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
8.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )
A.10° B.15° C.20° D.25°
9.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )
A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行
10.如图,在Rt△ABC 中,,D、E是斜边BC 上 两点,且∠DAE=45°,将△绕点顺时针旋转90后,得到△,连接 ,下列结论:①△≌△;②△∽△;③; ④其中正确的是( )
A.①②④; B.②③④; C.①②③; D.①③④.
二、填空题:(每小题3分,共18分)
11.等边三角形至少旋转 度才能与自身重合。
12.如图,图形①经过______变化成图形②,图形②经过_____变化成图形③。(填“平移”或“旋转”)
13.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则△ABB′是 三角形。
14.如图,把△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是 。
15.如图,将左边的“心形”绕点O顺时针旋转95°得到右边的“心形”,如果∠BOC=75°,则A、B、C三点的对应点分别是 ,∠DOF= 度,∠COD= 度。
16.如图,若将△ABO(O为坐标原点)绕点O顺时针旋转180°后得到△A'B'O,则A点的对应点A'点的坐标是________;△ABO内有一点P(m,n),则△A'B'O内与点P对应的点Q的坐标是 。
三、解答题:(17、18题每题8分,19-22题每题9分,共52分)
17.如图,在△ABC中,AD是中线。
(1)(3分)读语句画图:延长AD到点E,使DE=AD,连结BE、CE;
(2)(4分)填空:点A与点 关于点 成中心对称,线段AB与线段 关于点 成中心对称;
(3)(4分)写出所有关于点D成中心对称的三角形。
18.如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″.请你画出△A′B′C′和△A″B″C″。
19.如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使CE=CB.连结DE,那么量出DE的长,就是A、B的距离,为什么?线段DE可以看作哪条线段平移或旋转得到。
20、如图,已知:
(1) AC的长等于_______.
(2)将向右平移2个单位得到,写出点的对应点的坐标;
(3) 将绕点按顺时针方向旋转后得到A1B1C1,写出A点对应点A1的坐标.
21.如图,已知四边形为正方形,经过旋转后能与重合.
(1)指出旋转的中心和旋转的方向、角度;
(2)若,求的长。
22.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
答案:
九年级数学第二十三章《旋转》单元测试题
1.D 2.C 3.B 4.C 5.B 6.C 7.B 8.B 9.B 10.D
11.120 12.平移,旋转 13.等边 14.55° 15.E、D、F,75,20 16.(3,-2),(-m,-n)
17.解:(1)如图:
(2)E,D,EC,D
(3)△ABD与△ECD;
△ACD与△EBD;
△ABE与△ECA;
△ABC与△ECB.
18.如图:
19.解:因为AC=CD,CE=CB,∠ACB=∠DCE
所以△ACB≌△DCE
所以DE=AB
DE可看作AB绕点C旋转180°得到。
20.(1).(2)(1,2).(3)(3,0).
21.解:(1)△BCE绕点B逆时针旋转90°可与△BAF重合;
(2)Rt△BCE中,BC=4,CE=3,由勾股定理得:BE=5,
由旋转知,BF=BE=5,∠EBF=90°,
由勾股定理得: EF=.
22.解:(1)不正确。若旋转至点F落在AB上时,
BF<AB,而DF>AD,即DF>AB,
则此时DF>BF.
(2)DG=BE.如图2,连接BE.
在正方形ABCD和正方形AEFG中,
AB=AD,AE=AG,∠DAB=∠GAE=90°,
所以∠DAG=∠BAE,所以△ABE≌△ADG,
所以DG=BE.
同课章节目录
