圆的一般方程[上学期]

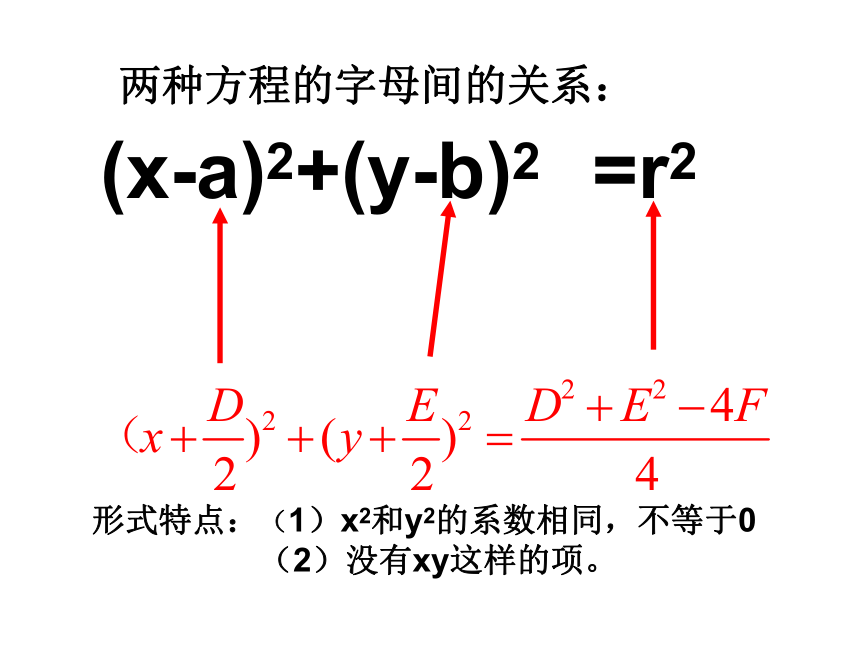
课件19张PPT。过一点求圆的切线的方程 1、求经过圆上一点M（x0,y0）的切线的方程 。2、求经过圆外一点M（x0,y0）的切线的方程 。圆的一般方程圆的标准方程是怎样的？圆的标准方程有什么特点？能直观看出圆的圆心与半经圆的一般方程得：x2+y2-2ax-2by+a2+b2-r2=0即：x2+y2+Dx+Ey+F=0（1）可见任何圆的方程都可以写成（1）式，不妨设：D＝－2a、E＝－2b、F＝a2+b2-r2(x-a)2+(y-b)2　=r2两种方程的字母间的关系：形式特点：（1）x2和y2的系数相同，不等于0
　　　　　（2）没有xy这样的项。反过来，形如（1）的方程的曲线是不是圆呢？圆的一般方程



[练习]1.下列方程各表示什么图形?原点(0,0)圆心(1,-2),半径圆心半径(1)(2)(3)
2.求下列各圆的半径和圆心坐标.
(1)

(2)

圆心半径为 3圆心半径为① A ＝ C ≠ 0圆的一般方程
例1. 求过三点O(0,0)，M1(1,1), M2(4,2)的圆的方程，并求这个圆的半径和圆心坐标 例1. 求过三点O(0,0)，M1(1,1), M2(4,2)的圆的方程，并求这个圆的半径和圆心坐标 解：设所求的圆的方程为 x2＋y2十Dx＋Ey＋F＝0．
用待定系数法，根据所给条件来确定D、E、F．
因为O、M1、M2在圆上，所以它们的坐标是方程的解解得F＝0，D＝?8，E＝6于是得到所求圆的方程x2+y2?8x+6y＝0．
∴圆的半径为5、圆心坐标是(4，－3)
[圆的一般方程与圆的标准方程在运用上的比较]
[习题示例] 求下列各圆的一般方程
(1)过点 圆心为点
(2)过三点
(1)若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单.(2).若已知三点求圆的方程,我们常常采用圆的一般方程用待定系数法求解. 例2. 已知一曲线是与定点O(0,0)，A(3,0)距离的比是求此曲线的轨迹方程，并画出曲线 的点的轨迹，化简得
x2+y2+2x?3＝0　　　　①
这就是所求的曲线方程．
把方程①的左边配方，得(x+1)2+y2＝4．
所以方程②的曲线是以C(?1，0)为圆心，2为半径的圆xyMAO .O..例2：已知一曲线是与两个定点O(0，0)，A(3，0)距离的比为 的点的轨迹，求此曲线的方程，并画出曲线。[简单的思考与应用]
(1)已知圆 的圆心坐标为
(-2,3),半径为4,则D,E,F分别等于
是圆的方程的充要条件是
(3)圆 与 轴相切,则这个圆截
轴所得的弦长是
(4)点 是圆 的一条弦的中点,
则这条弦所在的直线方程是
10. [课堂小结]
①若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单.(1)本节课的主要内容是圆的一般方程,其表达式为(用配方法求解)(3)给出圆的一般方程,如何求圆心和半径? (2)[圆的一般方程与圆的标准方程的联系]一般方程标准方程(圆心,半径)(4)要学会根据题目条件,恰当选择圆方程形式:②若已知三点求圆的方程,我们常常采用圆的一般方程用待定系数法求解.
(5)本节课用的数学方法和数学思想方法:①数学方法:②数学思想方法:11. [作业](求圆心和半径). (原则是不重复,不遗漏)配方法 (ⅰ) 问题转化和分类讨论的思想 (待定系数法)[如习题示例(2)](ⅱ)方程的思想(ⅲ)数形结合的思想