二次函数与反比例函数综合练习

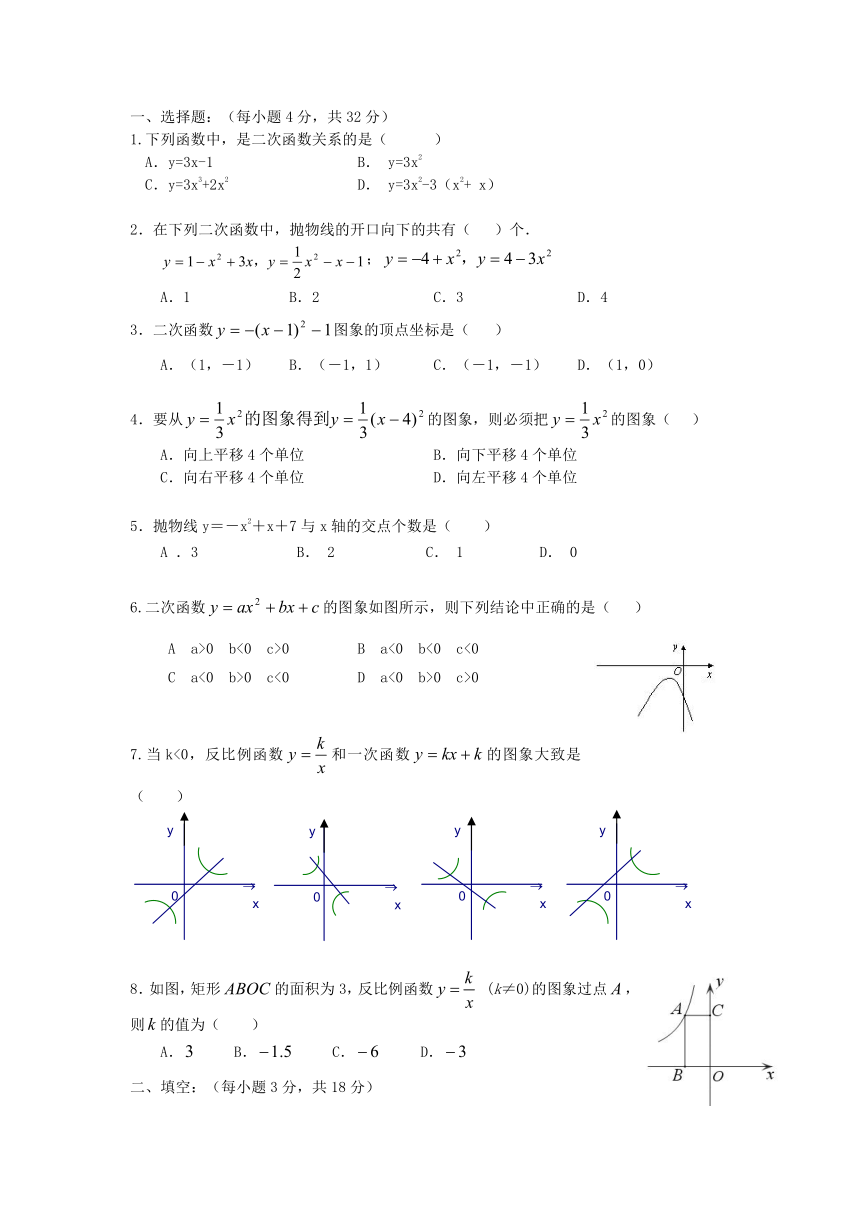
一、选择题：（每小题4分，共32分）　
1.下列函数中，是二次函数关系的是（ ）　　
A．y=3x-1 B． y=3x2　　　
C．y=3x3+2x2 D． y=3x2-3（x2+ x）　
　
2．在下列二次函数中，抛物线的开口向下的共有（ ）个．　　　
；　
A．1 B．2 C．3 D．4　
3．二次函数图象的顶点坐标是（ ）　
A．（1，－1） B．（－1，1） C．（－1，－1） D．（1，0）　
　　　
4．要从的图象，则必须把的图象（ ）　
A．向上平移4个单位 B．向下平移4个单位　
C．向右平移4个单位 D．向左平移4个单位　
　　　
5．抛物线y＝－x2＋x＋7与x轴的交点个数是（ ）　
A ．3 B． 2 C． 1 D． 0　　
　
6.二次函数的图象如图所示，则下列结论中正确的是（ ）　
A a>0 b<0 c>0 B a<0 b<0 c<0　　
C a<0 b>0 c<0 D a<0 b>0 c>0 　
　　　
　
7.当k<0，反比例函数和一次函数的图象大致是（ ）　　　
　　　
　　　
　
　　　
8．如图，矩形的面积为3，反比例函数 (k≠0)的图象过点，则的值为（ ）　
A． 　 B． C． D．　　
二、填空：（每小题3分，共18分）　
9．若双曲线y =经过点A（-2，3），则m的值为 ．　　
10.函数的二项式系数为 ；一次项系数为 ；常数项为 ．　
11．二次函数中，对称轴是直线 ，顶点坐标是_________，当X= 时，函数Y有最大值是 。　
12．已知反比例函数 y＝－ 的图像经过P（－2，m），则 m＝ ；　　　
当 x＜0 时，y 随 x 的增大而 ．　　　
　　
13．已知：二次函数y＝ax2 –x＋a2－1的图像如右图，则a的值是___ _．　　
　　　
14．已知：点（2，m），（b，m）是抛物线( a ≠0 )上两点，则抛物线的对称轴方程为 （用含有b或m的式子表示）　　
　
　　　
三、解答题： 　
15．（6分）已知二次函数的图像经过A（0，1），B（2，－1）两点．　　
（1）求和的值；（2）试判断点P（－1，2）是否在此函数图像上？　
　
　　　
　　　
　　
　　
　　
　
　　
　　
　　
16．（共14分）已知二次函数 y＝x2－4x-5 ．　　
把它用配方法化成 y＝a (x－h)2＋k 的形式； 　　
　
　　　
　　
　　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　 　
　　　
写出图像的开口方向．对称轴和顶点坐标； 　　
　　
　
求出函数图像与两坐标轴的交点坐标； 　　　
　
　
画出此函数图象的示意图； 　
　　　
　　　
　　　
　　　
　　　
　　　
　
　　
　　　
（5）根据图象回答：①x 时，y有最 值，最值是 ；
②当x 时，y>0；当x 时，y<0；
③当x 时，y随x的增大而增大；当x 时，y随x的增大而减小． 　
　　
17.（6分）　　　
已知二次函数y = ax2 ＋bx ＋c中，函数y与自变量x的部分对应值如下表：　　　
x　 …　　 －1　 0　 1　 2　　 3　　 4　　　 …　　　
y　　　 …　　　 10　　 1　　 －2　　　 1　　 10　 25　　 …　
（1）求这个二次函数的解析式；　　　
（2）写出这个二次函数的顶点坐标．　　
　　
　　　
　
　　
18．（ 6分）已知函数图像经过点（-2、k），试求函数y=kx-1的图像与坐标轴围成的三角形的面积。　　
　
　　
　　
　　　
　
　　　
　　　
　
　　　
　　　
　　　
　　　
19．（ 6分） 某地要建造一个圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰好在水面中心，安装在柱子顶端A处的喷头向外喷水， 水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上，抛物线的形状如图4(1)和(2)所示，建立直角坐标系，水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=－x2+2x+，请回答下列问题.　　
(1)柱子OA的高度为多少米 　　
(2)喷出的水流距水平面的最大高度是多少 　
(3)若不计其他因素，水池的半径至少要多少米， 才能使喷出的水流不至于落在池外.　　
　　　
　　　
　
　　
　　　
　
　　
　　
　
　　　
　
　
　　
　　　
　
20.（6分）已知：抛物线的解析式为y=x2-（2m-1）x+m2-m．　　
（1）求证：此抛物线与x轴必有两个不同的交点；　　　
（2）若此抛物线与直线y=x-3m+4的一个交点在y轴上，求m的值．　　
　　　
　　　
　　
　
　　
　　
　
　　　
　
　　　
　
　　
　
21.（本小题7分）已知抛物线y＝ax2＋bx＋c（a0）与x轴的两交点的横坐标分别是－1和3，与y轴交点的纵坐标是－3．　
（1）确定抛物线的解析式；　
（2）在所给的平面直角坐标系中，画出这个二次函数的示意图；　
（3）根据图象回答：当自变量x的取值范围满足什么条件时，y＜0？　
　
　
　　
　　
　　
　
　
　
　　
　　　
　　　
　　　
　　
　
　　
　　
　　
22．（本小题7分）如图，在平面直角坐标系中， 一次函数的图象与反比例函数的图象的一个交点为。　　
⑴ 求反比例函数的解析式；　
⑵ 若是坐标轴上一点，且满足，直接写出点的坐标。　　
　　
　
　　　
　　　
　
　　
　　　
　　
　　
23.（本小题7分） 已知关于的一元二次方程有实数根，为正整数.　
（1）求的值；　
（2）当此方程有两个非零的整数根时，将关于的二次函数的图象向下平移8个单位，求平移后的图象的解析式；　
　　　
　
　　　
　　　
　
　　　
　　
　　
　　
　　　
　　　
　　
　　
　　
　　　
24．(7分)如图，抛物线经过、两点，与轴交于另一点．　　　
（1）求抛物线的解析式；　　
（2）已知点在第一象限的抛物线上，求点关于直线对称的点的坐标；　　　
（3）在（2）的条件下，连接，点为轴上一点，且，求点的坐标．　　　
　　
　　　
　　　
　　　
　　
　　　
　　
　　　
　　　
　　
　
　　　
　　　
　　　
　　　
　　　
　
　
　
　
　
　　　
　
　　　
　
　
　
　　　
　　　
　　　
25．（8分）在平面直角坐标系中，二次函数的图象与轴交于、两点（点在点左侧），与轴交于点.　
⑴ 求点的坐标；　　
⑵ 当时，求的值；　　
⑶ 已知一次函数，点是轴上的一个动点，在⑵的条件下，过点垂直于 轴的直线交这个一次函数的图象于点，交二次函数的图象于点。若只有当时，点位于点的上方，求这个一次函数的解析式。　　
　
　
　
　　　
　　　
　
　　
　　
　
　　
　　
　　
　
　　　
　
　　　
　　
　　　
　　　
　　　
　　
　
　　
　　
　　
　
　
　　　
　
O　
　　　
图4　　
x　　　
y　　
O　
　
y　　
x　　　
O　
A　
B　
C