2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册1.3空间向量及其运算的坐标表示 讲义
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册1.3空间向量及其运算的坐标表示 讲义 |

|
|
| 格式 | docx | ||
| 文件大小 | 994.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 09:00:29 | ||
图片预览

文档简介
1.3.1空间直角坐标系
【知识梳理】
知识点一:空间直角坐标系定义:
在空间选定一点和一个单位正交基底 . 以点为原点,分别以,,的方向为正方向、以它们的长为单位长度建立三条数轴:轴、轴、轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系,叫做原点,,,都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为平面,平面,平面,它们把空间分成八个部分.
知识点二:空间直角坐标系的画法
借鉴在立体几何中学习的斜二测画法,在画空间直角坐标系时,让轴与轴所成的角为(或),即(或),画轴与轴垂直,即.
知识点三:空间点的坐标表示
在单位正交基底下与向量对应的有序实数组,,,叫做点在空间直角坐标系中的坐标,记做,,.
知识点四:空间向量的坐标表示
因为空间向量是自由的,我们在空间直角坐标系中可以作. 由空间向量基本定理,存在唯一的有序实数组,,,使,有序实数组,,叫做在空间直角坐标系中的坐标,上式可简记为,,那么,即点或者向量的坐标就是,,.
【例题精讲】
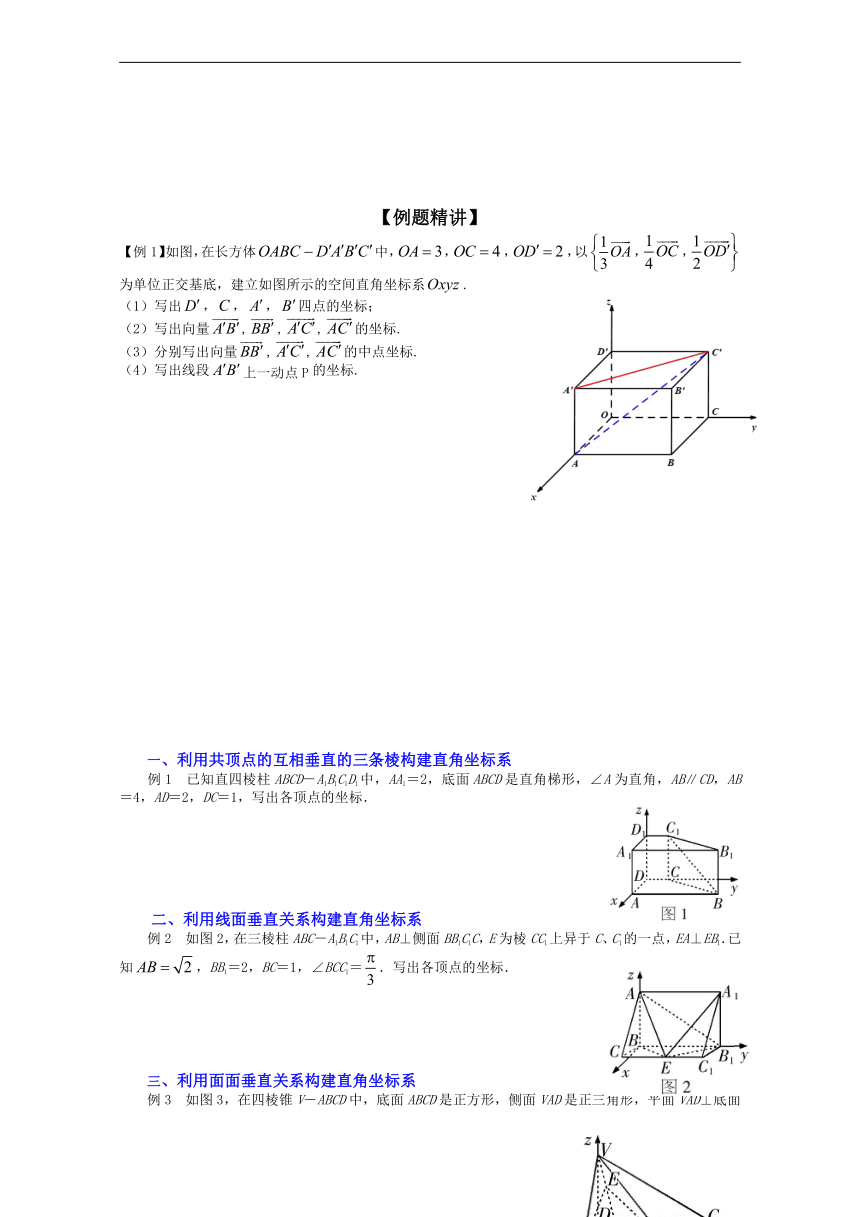
【例1】如图,在长方体中,,,,以,,为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出,,,四点的坐标;
(2)写出向量,,,的坐标.
(3)分别写出向量,,的中点坐标.
(4)写出线段上一动点P的坐标.
一、利用共顶点的互相垂直的三条棱构建直角坐标系
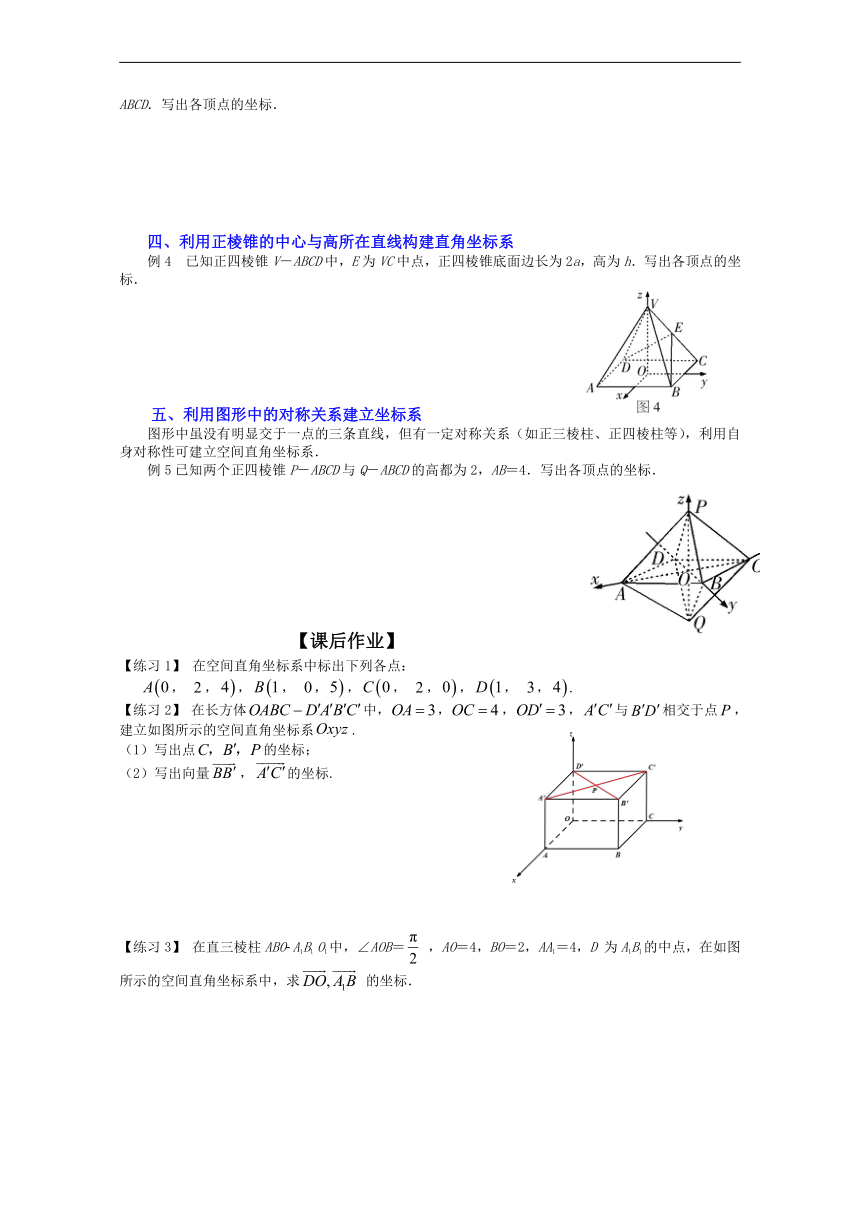
例1 已知直四棱柱ABCD-A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=1,写出各顶点的坐标.
二、利用线面垂直关系构建直角坐标系
例2 如图2,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1.已知,BB1=2,BC=1,∠BCC1=.写出各顶点的坐标.
三、利用面面垂直关系构建直角坐标系
例3 如图3,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.写出各顶点的坐标.
四、利用正棱锥的中心与高所在直线构建直角坐标系
例4 已知正四棱锥V-ABCD中,E为VC中点,正四棱锥底面边长为2a,高为h.写出各顶点的坐标.
五、利用图形中的对称关系建立坐标系
图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.
例5已知两个正四棱锥P-ABCD与Q-ABCD的高都为2,AB=4.写出各顶点的坐标.
【课后作业】
【练习1】 在空间直角坐标系中标出下列各点:
, ,,, ,,, ,,, ,.
【练习2】 在长方体中,,,,与相交于点,建立如图所示的空间直角坐标系.
(1)写出点的坐标;
(2)写出向量,的坐标.
【练习3】 在直三棱柱ABO A1B1 O1中,∠AOB= ,AO=4,BO=2,AA1=4,D 为A1B1的中点,在如图所示的空间直角坐标系中,求 的坐标.
1.3.2空间向量运算的坐标表示
【知识梳理】
知识点一:空间向量运算的坐标表示
设 ,空间向量的坐标运算法则如下表所示:
运算 坐标表示
加法
减法
数乘
数量积 =①
知识点二:空间向量的平行、垂直、模与夹角公式的坐标表示
1.空间向量的平行、垂直、模与夹角公式的坐标表示:
设 ,当 时,
平行
垂直 ___________________
模 _______________
夹角公式
2.空间向量的坐标及两点间的距离公式:
在空间直角坐标系中,设, ,则
(1)____________________
(2)__________________________
【例题精讲】
【例1】设,向量, ,则( )
A. B. C.3 D.4
【例2】如图,在空间直角坐标系中,正方体的棱长为2,,分别是, 的中点.
(1)求证;
(2)求与所成角的余弦值.
题型一 空间向量的坐标表示
已知点,点关于轴的对称点的坐标为( )
已知点,则线段的中点关于平面oyz对称的点的坐标为( )
题型二 空间向量线性运算的坐标表示
3、已知向量则向量=( )
4、若向量则( )
题型三 空间向量数量积的坐标表示
5、已知,则向量在上的投影向量为( )
6、若向量的坐标满足,则等于( )
题型四 利用空间向量的坐标运算解决平行和垂直问题
若在中,,则的值为( )
已知,若,则的取值范围为( )
题型五 利用空间向量的坐标运算求夹角和模
若向量,且与的夹角的余弦值为,则实数的值为( )
10、已知点
(1)若为线段的中点,求线段的长;
(2)若,且,求的值,并求此时向量与夹角的余弦值.
【课后作业】
1.求:
(1);
(2);
(3);
(4).
2.且.求的值.
3.已知.
(1)若,分别求λ与m的值;
(2)若,且与垂直,求.
4.如图,在棱长为1的正方体中,为的中点, ,分别在棱,上,,.
(1)求的长.
(2)求与所成角的余弦值.
【知识梳理】
知识点一:空间直角坐标系定义:
在空间选定一点和一个单位正交基底 . 以点为原点,分别以,,的方向为正方向、以它们的长为单位长度建立三条数轴:轴、轴、轴,它们都叫做坐标轴. 这时我们就建立了一个空间直角坐标系,叫做原点,,,都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为平面,平面,平面,它们把空间分成八个部分.
知识点二:空间直角坐标系的画法
借鉴在立体几何中学习的斜二测画法,在画空间直角坐标系时,让轴与轴所成的角为(或),即(或),画轴与轴垂直,即.
知识点三:空间点的坐标表示
在单位正交基底下与向量对应的有序实数组,,,叫做点在空间直角坐标系中的坐标,记做,,.
知识点四:空间向量的坐标表示
因为空间向量是自由的,我们在空间直角坐标系中可以作. 由空间向量基本定理,存在唯一的有序实数组,,,使,有序实数组,,叫做在空间直角坐标系中的坐标,上式可简记为,,那么,即点或者向量的坐标就是,,.
【例题精讲】
【例1】如图,在长方体中,,,,以,,为单位正交基底,建立如图所示的空间直角坐标系.
(1)写出,,,四点的坐标;
(2)写出向量,,,的坐标.
(3)分别写出向量,,的中点坐标.
(4)写出线段上一动点P的坐标.
一、利用共顶点的互相垂直的三条棱构建直角坐标系
例1 已知直四棱柱ABCD-A1B1C1D1中,AA1=2,底面ABCD是直角梯形,∠A为直角,AB∥CD,AB=4,AD=2,DC=1,写出各顶点的坐标.
二、利用线面垂直关系构建直角坐标系
例2 如图2,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1.已知,BB1=2,BC=1,∠BCC1=.写出各顶点的坐标.
三、利用面面垂直关系构建直角坐标系
例3 如图3,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.写出各顶点的坐标.
四、利用正棱锥的中心与高所在直线构建直角坐标系
例4 已知正四棱锥V-ABCD中,E为VC中点,正四棱锥底面边长为2a,高为h.写出各顶点的坐标.
五、利用图形中的对称关系建立坐标系
图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.
例5已知两个正四棱锥P-ABCD与Q-ABCD的高都为2,AB=4.写出各顶点的坐标.
【课后作业】
【练习1】 在空间直角坐标系中标出下列各点:
, ,,, ,,, ,,, ,.
【练习2】 在长方体中,,,,与相交于点,建立如图所示的空间直角坐标系.
(1)写出点的坐标;
(2)写出向量,的坐标.
【练习3】 在直三棱柱ABO A1B1 O1中,∠AOB= ,AO=4,BO=2,AA1=4,D 为A1B1的中点,在如图所示的空间直角坐标系中,求 的坐标.
1.3.2空间向量运算的坐标表示
【知识梳理】
知识点一:空间向量运算的坐标表示
设 ,空间向量的坐标运算法则如下表所示:
运算 坐标表示
加法
减法
数乘
数量积 =①
知识点二:空间向量的平行、垂直、模与夹角公式的坐标表示
1.空间向量的平行、垂直、模与夹角公式的坐标表示:
设 ,当 时,
平行
垂直 ___________________
模 _______________
夹角公式
2.空间向量的坐标及两点间的距离公式:
在空间直角坐标系中,设, ,则
(1)____________________
(2)__________________________
【例题精讲】
【例1】设,向量, ,则( )
A. B. C.3 D.4
【例2】如图,在空间直角坐标系中,正方体的棱长为2,,分别是, 的中点.
(1)求证;
(2)求与所成角的余弦值.
题型一 空间向量的坐标表示
已知点,点关于轴的对称点的坐标为( )
已知点,则线段的中点关于平面oyz对称的点的坐标为( )
题型二 空间向量线性运算的坐标表示
3、已知向量则向量=( )
4、若向量则( )
题型三 空间向量数量积的坐标表示
5、已知,则向量在上的投影向量为( )
6、若向量的坐标满足,则等于( )
题型四 利用空间向量的坐标运算解决平行和垂直问题
若在中,,则的值为( )
已知,若,则的取值范围为( )
题型五 利用空间向量的坐标运算求夹角和模
若向量,且与的夹角的余弦值为,则实数的值为( )
10、已知点
(1)若为线段的中点,求线段的长;
(2)若,且,求的值,并求此时向量与夹角的余弦值.
【课后作业】
1.求:
(1);
(2);
(3);
(4).
2.且.求的值.
3.已知.
(1)若,分别求λ与m的值;
(2)若,且与垂直,求.
4.如图,在棱长为1的正方体中,为的中点, ,分别在棱,上,,.
(1)求的长.
(2)求与所成角的余弦值.
