北师大版七年级数学下册1.6 完全平方公式 同步练习 (word版 含解析)
文档属性
| 名称 | 北师大版七年级数学下册1.6 完全平方公式 同步练习 (word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 00:00:00 | ||
图片预览



文档简介
北师大版七下 1.6 完全平方公式
一、选择题(共11小题)
1. 若 满足 的形式,则 等于
A. B. C. D.
2. 下列各式计算正确的是
A. B.
C. D.
3. 已知 ,,则 等于
A. B. C. D.
4. 有若干张面积分别为 ,, 的正方形和长方形纸片,阳阳从中抽取了 张面积为 的正方形纸片, 张面积为 的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为 的正方形纸片
A. 张 B. 张 C. 张 D. 张
5. 若 ,, 是正数,下列各式,从左到右的变形不能用下图验证的是
A.
B.
C.
D.
6. 利用完全平方公式计算 得
A. B. C. D.
7. 如图,在一块边长为 的红色正方形彩纸上,两纵两横的 条宽度为 的黄色矩形彩带把正方形彩纸分成 块,下面是四个计算剩余红色彩纸面积的代数式:① ,② ,③ ,④ ,其中正确的有
A. ② B. ①③ C. ①④ D. ④
8. 图①是一个长为 ,宽为 ()的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是
A. B. C. D.
9. 如图所示,长为 ,宽为 的长方形的周长为 ,面积为 ,则 的值为
A. B. C. D.
10. 观察下列一组图形,其中图形①中共有 颗星,图形②中共有 颗星,图形③中共有 颗星,图形④中共有 颗星,,按此规律,图形⑧中星星的颗数是
A. B. C. D.
11. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共5小题)
12. 若 ,则 .
13. 已知 ,,,且 ,则 的值等于 .
14. 已知 ,则代数式 的值为 .
15. 计算: .
16. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
三、解答题(共6小题)
17. 已知 ,.求:
(1) 的值;
(2) 的值.
18. 已知 ,求 的值.
19. 有一张边长为 厘米的正方形桌面,因为实际需要,需将正方形边长增加 厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:,对于方案一,小明是这样验证的:.
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
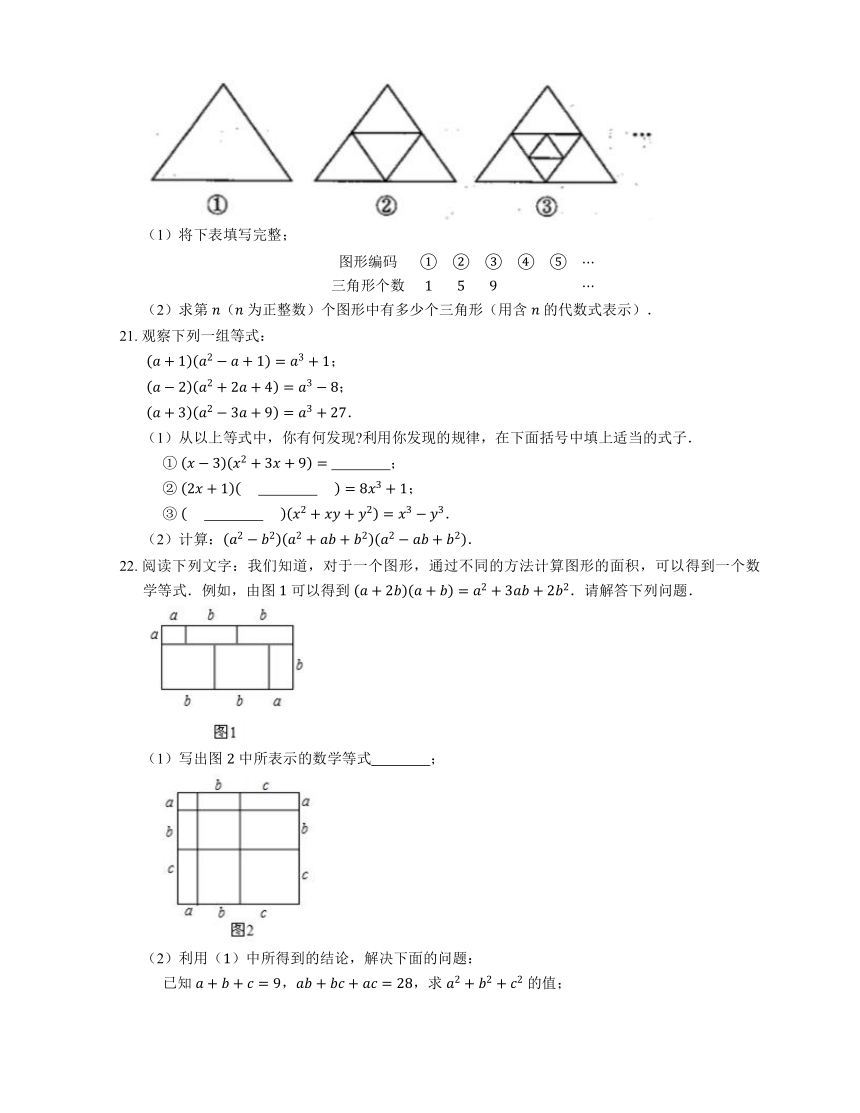
20. 图①是一个三角形,分别连接这个三角形三边的中点,得到图②,再分别连接图②中间小三角形三边的中点,得到图③,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下列问题:
(1)将下表填写完整;
(2)求第 ( 为正整数)个图形中有多少个三角形(用含 的代数式表示).
21. 观察下列一组等式:
;
;
.
(1)从以上等式中,你有何发现 利用你发现的规律,在下面括号中填上适当的式子.
① ;
② ;
③ .
(2)计算:.
22. 阅读下列文字:我们知道,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如,由图 可以得到 .请解答下列问题.
(1)写出图 中所表示的数学等式 ;
(2)利用()中所得到的结论,解决下面的问题:
已知 ,,求 的值;
(3)小明想用类似方法解释多项式乘法 ,那么需要用长为 和宽为 纸片 张;
(4)图 中给出了若干个边长为 和边长为 的小正方形纸片,若干个长为 、宽为 的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:.
答案
1. A
2. B
3. D
4. B
【解析】 边长为 的正方形的面积为 ,
还需面积为 的正方形纸片 张.
5. D
【解析】依据①②③④四部分的面积可得 ,故A能验证;依据⑤⑥两部分的面积可得 ,故B能验证;依据整个图形的面积可得 ,故C能验证;图中不存在长为 ,宽为 的长方形,故D不能验证.故选D.
6. D
【解析】
7. C
【解析】根据题意可知,剩余彩纸可以拼成边长为 的正方形,所以剩余彩纸面积 ;由题图可得,剩余彩纸面积 .故选C.
8. C
【解析】由题意可得,正方形的边长为 ,
故正方形的面积为 ,
又 原矩形的面积为 ,
中间空的部分的面积 .
9. D
【解析】由题意可知 ,,
,
.
故选D.
10. C
【解析】设图形 中星星的颗数是 ( 为自然数),
观察,发现规律:,,,,,
所以 .
令 ,则 .
11. D 【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
12.
13.
【解析】,,,
,,,
.
14.
【解析】,
,
.
15.
16. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
17. (1) .
(2) .
18.
当 时,.
19. 由题意可得,
方案二:
方案三:
20. (1) ;
【解析】图①有一个三角形,在此基础上,以后每连接一次中间三角形三边的中点,就多出 个三角形,
因此第 个图形中三角形的个数为 .
(2) 个.
21. (1) ;;
(2) .
22. (1)
(2)
(3)
(4)
一、选择题(共11小题)
1. 若 满足 的形式,则 等于
A. B. C. D.
2. 下列各式计算正确的是
A. B.
C. D.
3. 已知 ,,则 等于
A. B. C. D.
4. 有若干张面积分别为 ,, 的正方形和长方形纸片,阳阳从中抽取了 张面积为 的正方形纸片, 张面积为 的长方形纸片,若他想拼成一个大正方形,则还需要抽取面积为 的正方形纸片
A. 张 B. 张 C. 张 D. 张
5. 若 ,, 是正数,下列各式,从左到右的变形不能用下图验证的是
A.
B.
C.
D.
6. 利用完全平方公式计算 得
A. B. C. D.
7. 如图,在一块边长为 的红色正方形彩纸上,两纵两横的 条宽度为 的黄色矩形彩带把正方形彩纸分成 块,下面是四个计算剩余红色彩纸面积的代数式:① ,② ,③ ,④ ,其中正确的有
A. ② B. ①③ C. ①④ D. ④
8. 图①是一个长为 ,宽为 ()的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是
A. B. C. D.
9. 如图所示,长为 ,宽为 的长方形的周长为 ,面积为 ,则 的值为
A. B. C. D.
10. 观察下列一组图形,其中图形①中共有 颗星,图形②中共有 颗星,图形③中共有 颗星,图形④中共有 颗星,,按此规律,图形⑧中星星的颗数是
A. B. C. D.
11. 我国宋朝数学家杨辉 年的著作《详解九章算法》给出了在 ( 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A. B. C. D.
二、填空题(共5小题)
12. 若 ,则 .
13. 已知 ,,,且 ,则 的值等于 .
14. 已知 ,则代数式 的值为 .
15. 计算: .
16. 如图是我国数学家发明的“杨辉三角”,此图揭示了 ( 为非负整数)的展开式的项数及其系数的有关规律.请你观察,并根据此规律写出 的展开式共有 项,第二项的系数是 , 的展开式共有 项,各项的系数和是 .
三、解答题(共6小题)
17. 已知 ,.求:
(1) 的值;
(2) 的值.
18. 已知 ,求 的值.
19. 有一张边长为 厘米的正方形桌面,因为实际需要,需将正方形边长增加 厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:,对于方案一,小明是这样验证的:.
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
20. 图①是一个三角形,分别连接这个三角形三边的中点,得到图②,再分别连接图②中间小三角形三边的中点,得到图③,按此方法继续下去,请你根据每个图中三角形个数的规律,完成下列问题:
(1)将下表填写完整;
(2)求第 ( 为正整数)个图形中有多少个三角形(用含 的代数式表示).
21. 观察下列一组等式:
;
;
.
(1)从以上等式中,你有何发现 利用你发现的规律,在下面括号中填上适当的式子.
① ;
② ;
③ .
(2)计算:.
22. 阅读下列文字:我们知道,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如,由图 可以得到 .请解答下列问题.
(1)写出图 中所表示的数学等式 ;
(2)利用()中所得到的结论,解决下面的问题:
已知 ,,求 的值;
(3)小明想用类似方法解释多项式乘法 ,那么需要用长为 和宽为 纸片 张;
(4)图 中给出了若干个边长为 和边长为 的小正方形纸片,若干个长为 、宽为 的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:.
答案
1. A
2. B
3. D
4. B
【解析】 边长为 的正方形的面积为 ,
还需面积为 的正方形纸片 张.
5. D
【解析】依据①②③④四部分的面积可得 ,故A能验证;依据⑤⑥两部分的面积可得 ,故B能验证;依据整个图形的面积可得 ,故C能验证;图中不存在长为 ,宽为 的长方形,故D不能验证.故选D.
6. D
【解析】
7. C
【解析】根据题意可知,剩余彩纸可以拼成边长为 的正方形,所以剩余彩纸面积 ;由题图可得,剩余彩纸面积 .故选C.
8. C
【解析】由题意可得,正方形的边长为 ,
故正方形的面积为 ,
又 原矩形的面积为 ,
中间空的部分的面积 .
9. D
【解析】由题意可知 ,,
,
.
故选D.
10. C
【解析】设图形 中星星的颗数是 ( 为自然数),
观察,发现规律:,,,,,
所以 .
令 ,则 .
11. D 【解析】由题意,,
可知,展开式中第二项为 ,
所以 展开式中含 项的系数是 .
12.
13.
【解析】,,,
,,,
.
14.
【解析】,
,
.
15.
16. ,,,
【解析】 的展开式有 项; 的展开式有 项; 的展开式有 项; 故 的展开式共有 项.由题中规律得 的展开式中第二项的系数为 , 的展开式中第二项的系数为 ,故 的展开式中第二项的系数为 .
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
的展开式中各项的系数和为 ;
故 的展开式中各项的系数和为 .
17. (1) .
(2) .
18.
当 时,.
19. 由题意可得,
方案二:
方案三:
20. (1) ;
【解析】图①有一个三角形,在此基础上,以后每连接一次中间三角形三边的中点,就多出 个三角形,
因此第 个图形中三角形的个数为 .
(2) 个.
21. (1) ;;
(2) .
22. (1)
(2)
(3)
(4)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
