北师大版九年级数学下册1.6 利用三角函数测高 同步练习 (word版 含解析)
文档属性
| 名称 | 北师大版九年级数学下册1.6 利用三角函数测高 同步练习 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 10:26:42 | ||
图片预览


文档简介
北师大版九下 1.6 利用三角函数测高
一、选择题(共13小题)
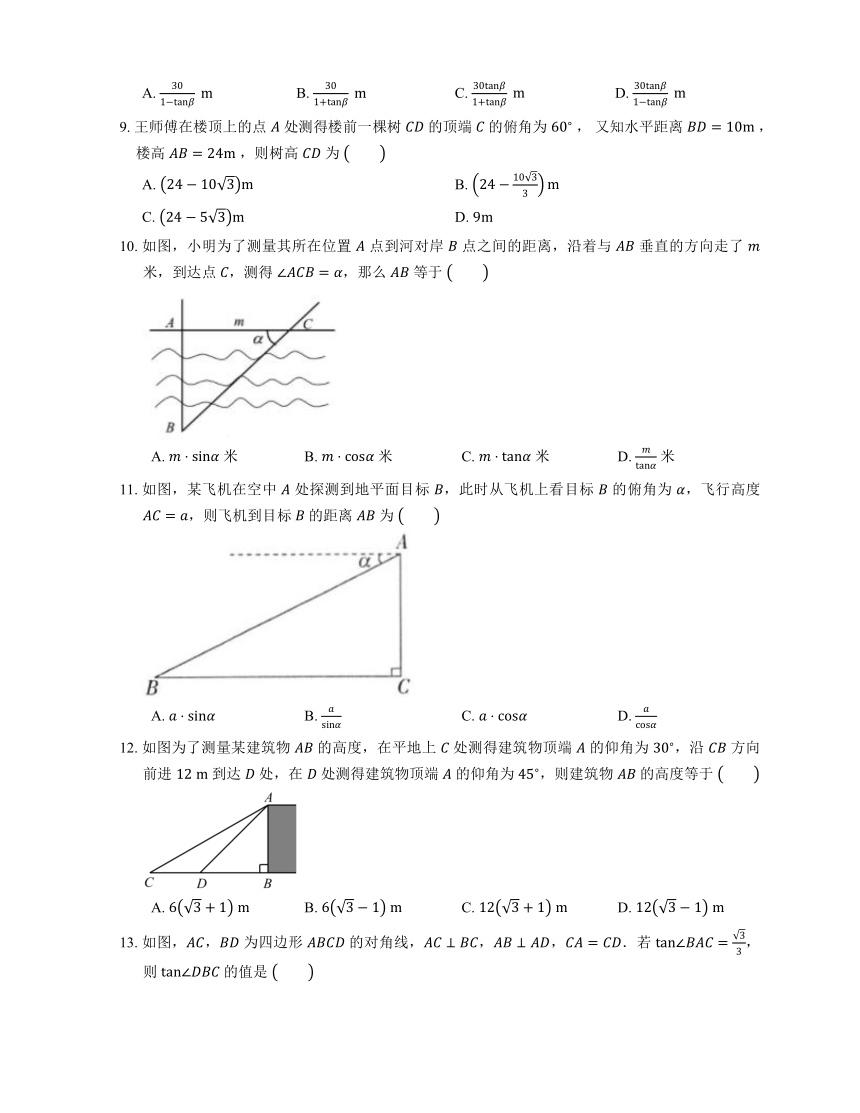
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如图,从点 观测点 的仰角是
A. B. C. D.
3. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
4. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
5. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:()在点 处放置测角仪,测得旗杆顶的仰角 ;()量得测角仪的高度 ;()量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
6. 如图,钓鱼竿 长 ,露在水面上的鱼线 长 ,某钓者想看看鱼钩上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则鱼竿转过的角度是
A. B. C. D.
7. 年 月 日,嫦娥四号探测器自主着陆在月球背面,实现人类探测器首次在月球背面软着陆.当时,中国已提前发射的“鹊桥”中继星正在地球、月球所在直线上的 点(第二拉格朗日点)附近,沿 点的动态平衡轨道飞行,为嫦娥四号着陆器和月球车提供地球、月球中继通信支持,保障嫦娥四号任务的完成与实施.
如图,已知月球到地球的平均距离约为 万千米, 点到月球的平均距离约为 万千米.某刻,测得线段 与 垂直,,则下列计算“鹊桥”中继星到地球的距离 的方法中正确的是
A.
B.
C.
D.
8. 在欧洲有很多古老而且美丽的中世纪建筑群,如图,古罗马教堂建筑物 的高为 ,从 点测得 点的仰角 等于 ,从 点看 点的俯角,因无法测得准确的角度,只能记为 ,则建筑物 的高度为
A. B. C. D.
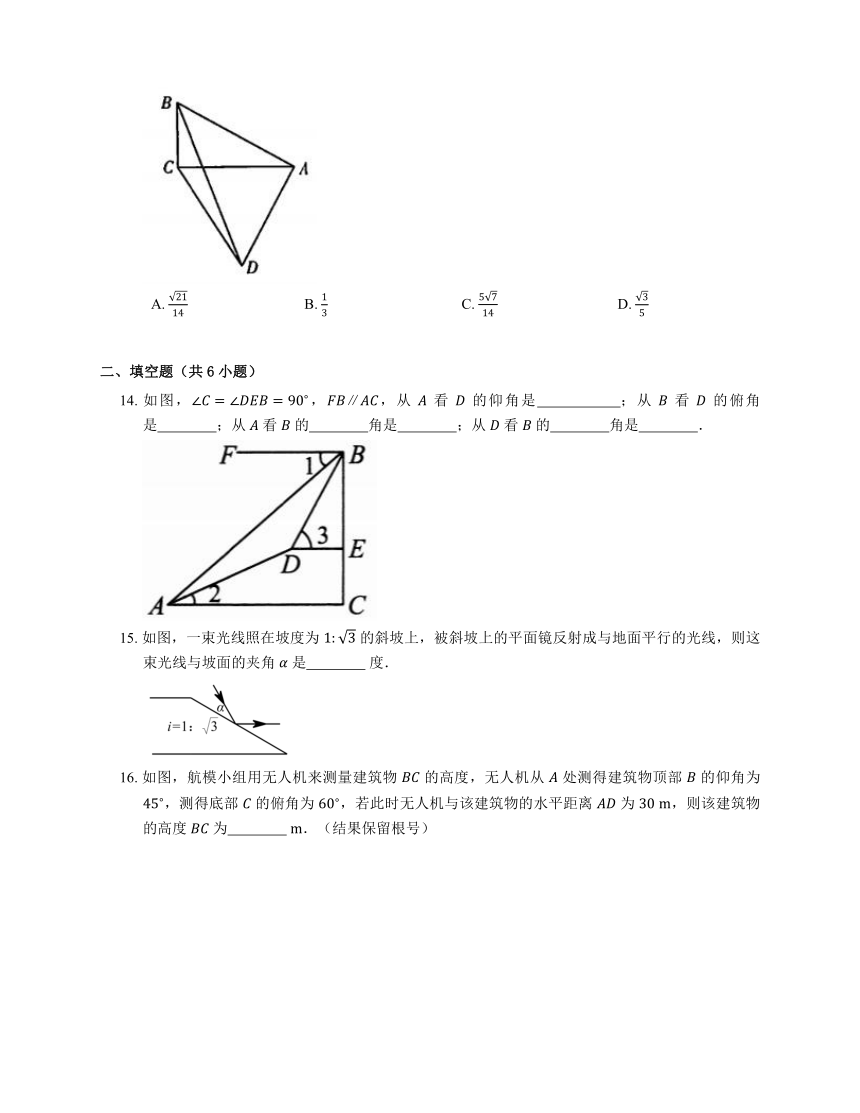
9. 王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 , 又知水平距离 ,楼高 ,则树高 为
A. B.
C. D.
10. 如图,小明为了测量其所在位置 点到河对岸 点之间的距离,沿着与 垂直的方向走了 米,到达点 ,测得 ,那么 等于
A. 米 B. 米 C. 米 D. 米
11. 如图,某飞机在空中 处探测到地平面目标 ,此时从飞机上看目标 的俯角为 ,飞行高度 ,则飞机到目标 的距离 为
A. B. C. D.
12. 如图为了测量某建筑物 的高度,在平地上 处测得建筑物顶端 的仰角为 ,沿 方向前进 到达 处,在 处测得建筑物顶端 的仰角为 ,则建筑物 的高度等于
A. B. C. D.
13. 如图,, 为四边形 的对角线,,,.若 ,则 的值是
A. B. C. D.
二、填空题(共6小题)
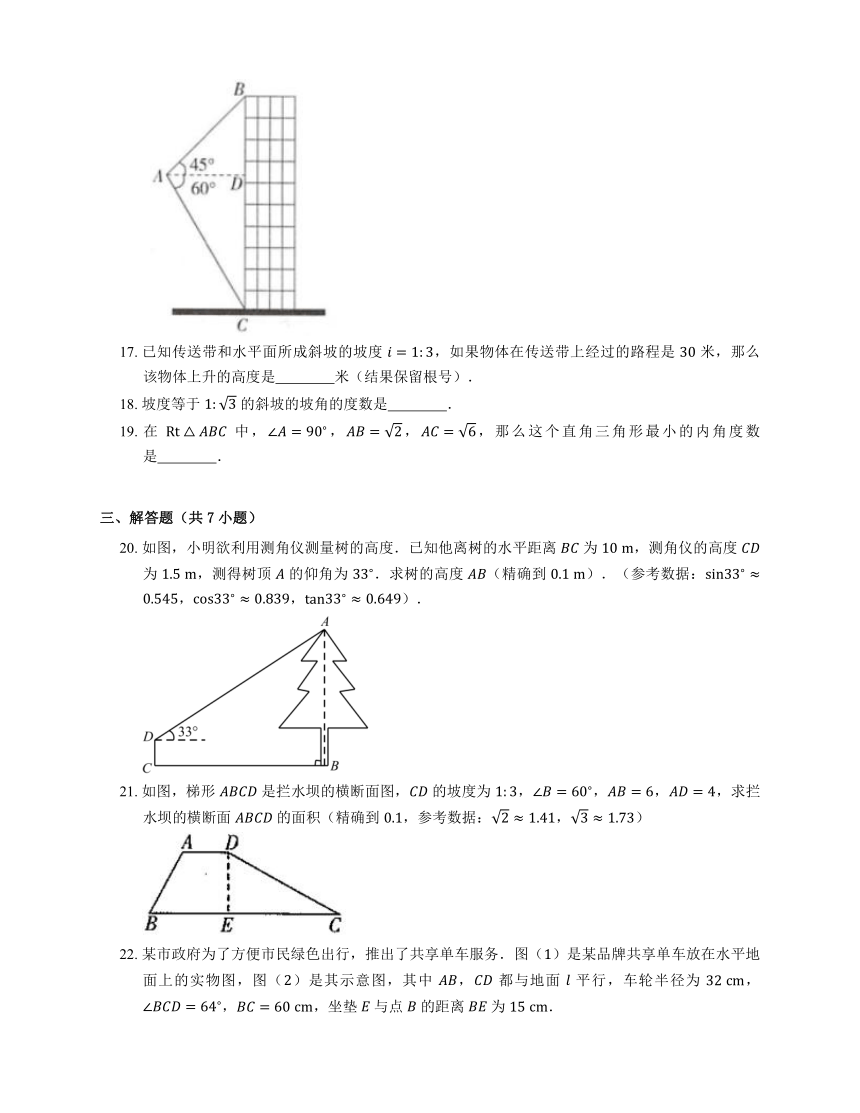
14. 如图,,,从 看 的仰角是 ;从 看 的俯角是 ;从 看 的 角是 ;从 看 的 角是 .
15. 如图,一束光线照在坡度为 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角 是 度.
16. 如图,航模小组用无人机来测量建筑物 的高度,无人机从 处测得建筑物顶部 的仰角为 ,测得底部 的俯角为 ,若此时无人机与该建筑物的水平距离 为 ,则该建筑物的高度 为 .(结果保留根号)
17. 已知传送带和水平面所成斜坡的坡度 ,如果物体在传送带上经过的路程是 米,那么该物体上升的高度是 米(结果保留根号).
18. 坡度等于 的斜坡的坡角的度数是 .
19. 在 中,,,,那么这个直角三角形最小的内角度数是 .
三、解答题(共7小题)
20. 如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离 为 ,测角仪的高度 为 ,测得树顶 的仰角为 .求树的高度 (精确到 ).(参考数据:,,).
21. 如图,梯形 是拦水坝的横断面图, 的坡度为 ,,,,求拦水坝的横断面 的面积(精确到 ,参考数据:,)
22. 某市政府为了方便市民绿色出行,推出了共享单车服务.图()是某品牌共享单车放在水平地面上的实物图,图()是其示意图,其中 , 都与地面 平行,车轮半径为 ,,,坐垫 与点 的距离 为 .
(结果精确到 ,参考数据:,,)
(1)求坐垫 到地面的距离;
(2)根据经验,当坐垫 到 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.
23. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在码头西端 的正西方向 千米处有一观察站 .某时刻测得一艘匀速直线航行的轮船位于 的北偏西 方向,且与 相距 千米的 处;经过 分钟,又测得该轮船位于 的正北方向,且与 相距 千米的 处.(参考数据:,)
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头 靠岸 请说明理由.
24. 如图 是某小型汽车的侧面示意图,其中矩形 表示该车的后备箱,在打开后备箱的过程中,箱盖 可以绕点 逆时针方向旋转,当旋转角为 时,箱盖 落在 的位置(如图 所示).已知 厘米, 厘米, 厘米.
(1)求点 到 的距离;
(2)求 , 两点的距离.
25. 天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道 处开始,沿 路线对索道进行检修维护.如图,已知 米, 米, 与水平线 的夹角是 , 与水平线 的夹角是 .求本次检修中,检修人员上升的垂直高度 约是多少米.(结果精确到 米,参考数据:)
26. 如图,在某信号塔 的正前方有一斜坡 ,坡角 ,斜坡的顶端 与塔底 的距离 米,小明在斜坡上的点 处测得塔顶 的仰角 , 米,且 ,(点 ,,,,,, 在同一平面内).
(1)填空: 度, 度;
(2)求信号塔的高度 (结果保留根号).
答案
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
3. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
4. B
5. A
6. C
【解析】由于钓鱼竿 ,露在水面上的鱼线 ,
由三角函数得 ,则 ;
把鱼竿 转动到 的位置,由于 ,,
由三角函数得 ,则 ,
所以鱼竿转过的角度是 .
7. B
【解析】在直角三角形 中,
,
,
在直角三角形 中,
,
.
8. A
【解析】如图,作 于点 ,
易知四边形 为矩形,
,,,
,
,
,
,,
在 中,,
,
解得 ,
则建筑物 的高度为 .
故选A.
9. A
10. C
11. B
【解析】由题意知 ,,,
在 中,,
.
12. A
【解析】,
.
,,
.
.
13. D
14. ,,仰,,仰,
15.
16.
【解析】 在 中,,,
.
在 中,
,
,
,
即该建筑物的高度 为 .
17.
【解析】如图,由题意,得斜坡 的坡度为 ,
过点 作 于点 ,
由坡度的定义,得 ,
设 米,则 米,
米,
,
米,
该物件体上升的高度是 米.
18.
19.
20. 米
21. 过点 作 于 ,
在 中,,
,,
.
的坡度比为 ,
,
,
.
22. (1) 如图(),过点 作 于点 ,
由题意知 ,,
.
故坐垫 到地面的距离为 .
(2) 如图(),过点 作 于点 ,
由题意知 ,
则 ,
.
23. (1) 如图,过点 作 于点 .
由题意,得 千米, 千米,.
(千米).
在 中,
(千米),
(千米).
在 中,
(千米).
该轮船航行的速度为 (千米/时).
(2) 如果轮船不改变航向继续航行,不能行至码头 靠岸.
理由如下:
如图,延长 交海岸线 于点 .
千米,,
.
,
在 中,
(千米).
,
该轮船不改变航向继续航行,不能行至码头 靠岸.
24. (1) 过点 作 ,垂足为点 ,交 于点 .
由题意得 (厘米),.
四边形 是矩形,
,
.
在 中,(厘米).
又 (厘米),(厘米),
(厘米).
(厘米)
答:点 到 的距离是 厘米.
(2) 连接 ,,,由题意得 ,,
是等边三角形,
.
四边形 是矩形,
.
在 中,(厘米),(厘米),
(厘米).
(厘米).
答:, 两点的距离是 厘米.
25. 如图,过点 作 于点 .
在 中, 米,,
(米),
(米).
在 中, 米,,
,
(米),
(米).
答:检修人员上升的垂直高度 约为 米.
26. (1) ;
【解析】因为 ,
所以 ,
又因为 ,
所以 ,
因为 ,
所以 ,
又因为 ,
所以 .
(2) 如图,过点 作 ,垂足为 ,延长 交 于点 ,
在 中,
因为 ,,
所以 ,
所以 ,
设 ,则 ,
,
在 中,
因为 ,
所以 ,
即 ,
,
即信号塔的高度 为 .
一、选择题(共13小题)
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如图,从点 观测点 的仰角是
A. B. C. D.
3. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
4. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
5. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:()在点 处放置测角仪,测得旗杆顶的仰角 ;()量得测角仪的高度 ;()量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
6. 如图,钓鱼竿 长 ,露在水面上的鱼线 长 ,某钓者想看看鱼钩上的情况,把鱼竿 转动到 的位置,此时露在水面上的鱼线 为 ,则鱼竿转过的角度是
A. B. C. D.
7. 年 月 日,嫦娥四号探测器自主着陆在月球背面,实现人类探测器首次在月球背面软着陆.当时,中国已提前发射的“鹊桥”中继星正在地球、月球所在直线上的 点(第二拉格朗日点)附近,沿 点的动态平衡轨道飞行,为嫦娥四号着陆器和月球车提供地球、月球中继通信支持,保障嫦娥四号任务的完成与实施.
如图,已知月球到地球的平均距离约为 万千米, 点到月球的平均距离约为 万千米.某刻,测得线段 与 垂直,,则下列计算“鹊桥”中继星到地球的距离 的方法中正确的是
A.
B.
C.
D.
8. 在欧洲有很多古老而且美丽的中世纪建筑群,如图,古罗马教堂建筑物 的高为 ,从 点测得 点的仰角 等于 ,从 点看 点的俯角,因无法测得准确的角度,只能记为 ,则建筑物 的高度为
A. B. C. D.
9. 王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 , 又知水平距离 ,楼高 ,则树高 为
A. B.
C. D.
10. 如图,小明为了测量其所在位置 点到河对岸 点之间的距离,沿着与 垂直的方向走了 米,到达点 ,测得 ,那么 等于
A. 米 B. 米 C. 米 D. 米
11. 如图,某飞机在空中 处探测到地平面目标 ,此时从飞机上看目标 的俯角为 ,飞行高度 ,则飞机到目标 的距离 为
A. B. C. D.
12. 如图为了测量某建筑物 的高度,在平地上 处测得建筑物顶端 的仰角为 ,沿 方向前进 到达 处,在 处测得建筑物顶端 的仰角为 ,则建筑物 的高度等于
A. B. C. D.
13. 如图,, 为四边形 的对角线,,,.若 ,则 的值是
A. B. C. D.
二、填空题(共6小题)
14. 如图,,,从 看 的仰角是 ;从 看 的俯角是 ;从 看 的 角是 ;从 看 的 角是 .
15. 如图,一束光线照在坡度为 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角 是 度.
16. 如图,航模小组用无人机来测量建筑物 的高度,无人机从 处测得建筑物顶部 的仰角为 ,测得底部 的俯角为 ,若此时无人机与该建筑物的水平距离 为 ,则该建筑物的高度 为 .(结果保留根号)
17. 已知传送带和水平面所成斜坡的坡度 ,如果物体在传送带上经过的路程是 米,那么该物体上升的高度是 米(结果保留根号).
18. 坡度等于 的斜坡的坡角的度数是 .
19. 在 中,,,,那么这个直角三角形最小的内角度数是 .
三、解答题(共7小题)
20. 如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离 为 ,测角仪的高度 为 ,测得树顶 的仰角为 .求树的高度 (精确到 ).(参考数据:,,).
21. 如图,梯形 是拦水坝的横断面图, 的坡度为 ,,,,求拦水坝的横断面 的面积(精确到 ,参考数据:,)
22. 某市政府为了方便市民绿色出行,推出了共享单车服务.图()是某品牌共享单车放在水平地面上的实物图,图()是其示意图,其中 , 都与地面 平行,车轮半径为 ,,,坐垫 与点 的距离 为 .
(结果精确到 ,参考数据:,,)
(1)求坐垫 到地面的距离;
(2)根据经验,当坐垫 到 的距离调整为人体腿长的 时,坐骑比较舒适.小明的腿长约为 ,现将坐垫 调整至坐骑舒适高度位置 ,求 的长.
23. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在码头西端 的正西方向 千米处有一观察站 .某时刻测得一艘匀速直线航行的轮船位于 的北偏西 方向,且与 相距 千米的 处;经过 分钟,又测得该轮船位于 的正北方向,且与 相距 千米的 处.(参考数据:,)
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头 靠岸 请说明理由.
24. 如图 是某小型汽车的侧面示意图,其中矩形 表示该车的后备箱,在打开后备箱的过程中,箱盖 可以绕点 逆时针方向旋转,当旋转角为 时,箱盖 落在 的位置(如图 所示).已知 厘米, 厘米, 厘米.
(1)求点 到 的距离;
(2)求 , 两点的距离.
25. 天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道 处开始,沿 路线对索道进行检修维护.如图,已知 米, 米, 与水平线 的夹角是 , 与水平线 的夹角是 .求本次检修中,检修人员上升的垂直高度 约是多少米.(结果精确到 米,参考数据:)
26. 如图,在某信号塔 的正前方有一斜坡 ,坡角 ,斜坡的顶端 与塔底 的距离 米,小明在斜坡上的点 处测得塔顶 的仰角 , 米,且 ,(点 ,,,,,, 在同一平面内).
(1)填空: 度, 度;
(2)求信号塔的高度 (结果保留根号).
答案
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
3. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
4. B
5. A
6. C
【解析】由于钓鱼竿 ,露在水面上的鱼线 ,
由三角函数得 ,则 ;
把鱼竿 转动到 的位置,由于 ,,
由三角函数得 ,则 ,
所以鱼竿转过的角度是 .
7. B
【解析】在直角三角形 中,
,
,
在直角三角形 中,
,
.
8. A
【解析】如图,作 于点 ,
易知四边形 为矩形,
,,,
,
,
,
,,
在 中,,
,
解得 ,
则建筑物 的高度为 .
故选A.
9. A
10. C
11. B
【解析】由题意知 ,,,
在 中,,
.
12. A
【解析】,
.
,,
.
.
13. D
14. ,,仰,,仰,
15.
16.
【解析】 在 中,,,
.
在 中,
,
,
,
即该建筑物的高度 为 .
17.
【解析】如图,由题意,得斜坡 的坡度为 ,
过点 作 于点 ,
由坡度的定义,得 ,
设 米,则 米,
米,
,
米,
该物件体上升的高度是 米.
18.
19.
20. 米
21. 过点 作 于 ,
在 中,,
,,
.
的坡度比为 ,
,
,
.
22. (1) 如图(),过点 作 于点 ,
由题意知 ,,
.
故坐垫 到地面的距离为 .
(2) 如图(),过点 作 于点 ,
由题意知 ,
则 ,
.
23. (1) 如图,过点 作 于点 .
由题意,得 千米, 千米,.
(千米).
在 中,
(千米),
(千米).
在 中,
(千米).
该轮船航行的速度为 (千米/时).
(2) 如果轮船不改变航向继续航行,不能行至码头 靠岸.
理由如下:
如图,延长 交海岸线 于点 .
千米,,
.
,
在 中,
(千米).
,
该轮船不改变航向继续航行,不能行至码头 靠岸.
24. (1) 过点 作 ,垂足为点 ,交 于点 .
由题意得 (厘米),.
四边形 是矩形,
,
.
在 中,(厘米).
又 (厘米),(厘米),
(厘米).
(厘米)
答:点 到 的距离是 厘米.
(2) 连接 ,,,由题意得 ,,
是等边三角形,
.
四边形 是矩形,
.
在 中,(厘米),(厘米),
(厘米).
(厘米).
答:, 两点的距离是 厘米.
25. 如图,过点 作 于点 .
在 中, 米,,
(米),
(米).
在 中, 米,,
,
(米),
(米).
答:检修人员上升的垂直高度 约为 米.
26. (1) ;
【解析】因为 ,
所以 ,
又因为 ,
所以 ,
因为 ,
所以 ,
又因为 ,
所以 .
(2) 如图,过点 作 ,垂足为 ,延长 交 于点 ,
在 中,
因为 ,,
所以 ,
所以 ,
设 ,则 ,
,
在 中,
因为 ,
所以 ,
即 ,
,
即信号塔的高度 为 .
