2022-2023年北师大版九年级数学下册2.5 二次函数与一元二次方程 同步练习 (word版 含解析)
文档属性
| 名称 | 2022-2023年北师大版九年级数学下册2.5 二次函数与一元二次方程 同步练习 (word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 565.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 10:57:40 | ||
图片预览



文档简介
北师大版九下 2.5 二次函数与一元二次方程
一、选择题(共10小题)
1. 抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A. 有两个不同的实数根 B. 有两个相同的实数根
C. 没有实数根 D. 无法判定
2. 下列二次函数的图象与 轴没有交点的是
A. B. C. D.
3. 抛物线 的开口向上,与 轴的交点在 轴的负半轴,那么方程 的两实数根的积
A. 大于零 B. 等于零 C. 小于零 D. 以上都不对
4. 若二次函数 的图象经过点 ,则方程 的解为
A. , B. ,
C. , D. ,
5. 如图,已知二次函数 的图象与正比例函数 的图象交于点 ,与 轴交于点 ,若 ,则 的取值范围是
A. B. C. D. 或
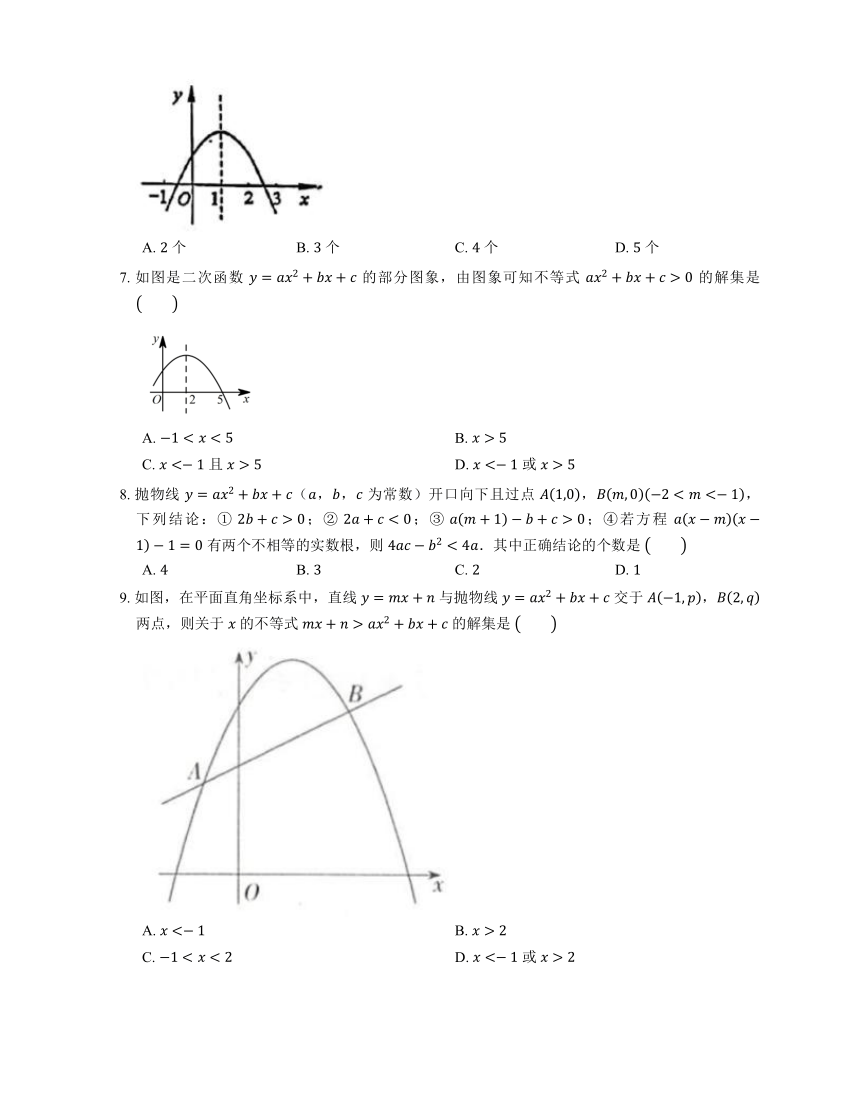
6. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
7. 如图是二次函数 的部分图象,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 抛物线 (,, 为常数)开口向下且过点 ,,下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是
A. B. C. D.
9. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
10. 已知抛物线 (,, 是常数,)经过点 ,,当 时,与其对应的函数值 .有下列结论:① ;②关于 的方程 有两个不等的实数根;③ .其中,正确结论的个数是
A. B. C. D.
二、填空题(共5小题)
11. 下图是抛物线 和一次函数 的图象,观察图象写出 时, 的取值范围 .
12. 已知函数 ,若使 成立的 值恰好有 个,则 的值为 .
13. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 ,,且 ,则 的取值范围是 .
14. 关于抛物线 ,给出下列结论:
①当 时,抛物线与直线 没有交点;
②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;
③若抛物线的顶点在点 ,, 所围成的三角形区域内(包括边界),则 .其中正确结论的序号是 .
15. 已知二次函数 ( 为常数),当 时,函数 有最小值 ,则 的值为 .
三、解答题(共7小题)
16. 已知二次函数 ( 为常数,且 ).
(1)求证:不论 为何值,该函数的图象与 轴总有公共点;
(2)设该函数的图象与 轴交于点 ,若点 在 轴上方,求 的取值范围;
(3)该函数图象所过的象限随 的值变化而变化,直接写出函数图象所经过的象限及对应的 的取值范围.
17. 已知关于 的二次函数 的图象的顶点 和其上一点 的坐标,求这个二次函数的解析式.
(1),.
(2),.
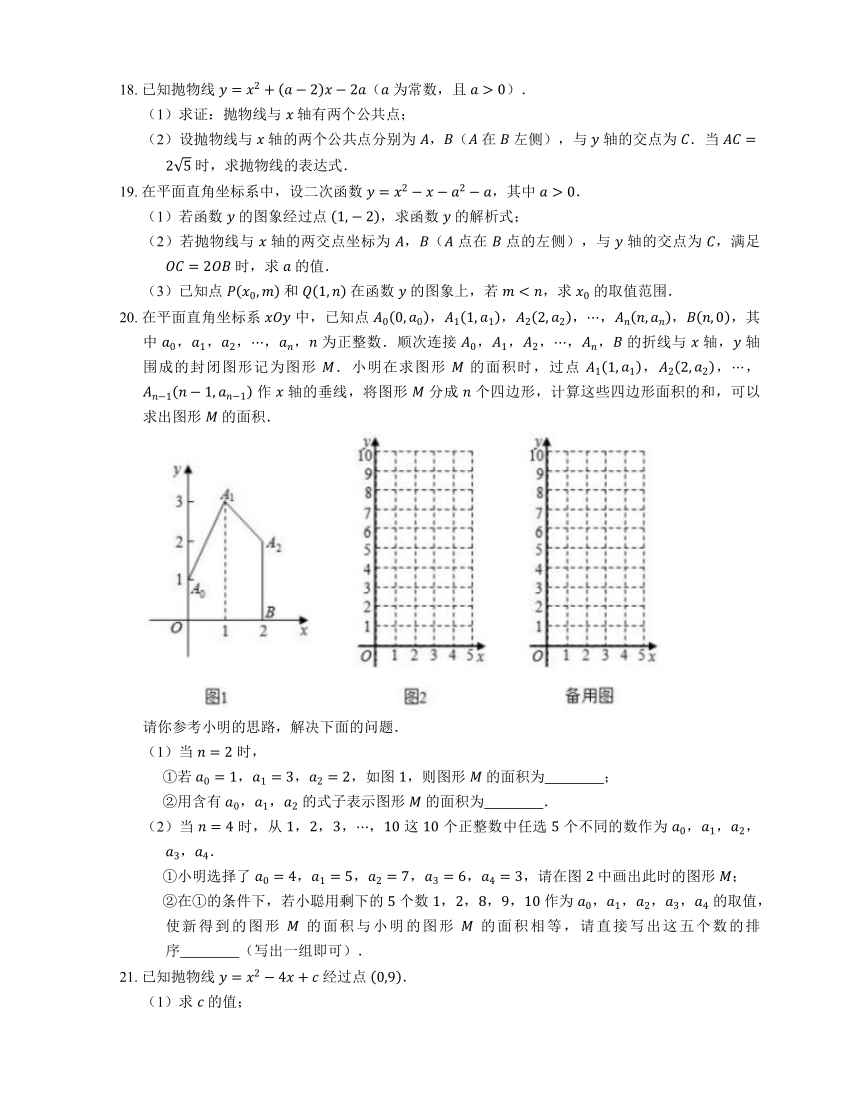
18. 已知抛物线 ( 为常数,且 ).
(1)求证:抛物线与 轴有两个公共点;
(2)设抛物线与 轴的两个公共点分别为 ,( 在 左侧),与 轴的交点为 .当 时,求抛物线的表达式.
19. 在平面直角坐标系中,设二次函数 ,其中 .
(1)若函数 的图象经过点 ,求函数 的解析式;
(2)若抛物线与 轴的两交点坐标为 ,( 点在 点的左侧),与 轴的交点为 ,满足 时,求 的值.
(3)已知点 和 在函数 的图象上,若 ,求 的取值范围.
20. 在平面直角坐标系 中,已知点 ,,,,,,其中 ,,,,, 为正整数.顺次连接 ,,,,, 的折线与 轴, 轴围成的封闭图形记为图形 .小明在求图形 的面积时,过点 ,,, 作 轴的垂线,将图形 分成 个四边形,计算这些四边形面积的和,可以求出图形 的面积.
请你参考小明的思路,解决下面的问题.
(1)当 时,
①若 ,,,如图 ,则图形 的面积为 ;
②用含有 ,, 的式子表示图形 的面积为 .
(2)当 时,从 ,,,, 这 个正整数中任选 个不同的数作为 ,,,,.
①小明选择了 ,,,,,请在图 中画出此时的图形 ;
②在①的条件下,若小聪用剩下的 个数 ,,,, 作为 ,,,, 的取值,使新得到的图形 的面积与小明的图形 的面积相等,请直接写出这五个数的排序 (写出一组即可).
21. 已知抛物线 经过点 .
(1)求 的值;
(2)若点 , 在该抛物线上,试比较 , 的大小.
22. 若抛物线 与 轴有交点,求 的取值范围.
答案
1. A
2. D
【解析】A.,此抛物线与 轴有两个交点,所以A选项错误;
B.,此抛物线与 轴有两个交点,所以B选项错误;
C.,此抛物线与 轴有1个交点,所以C选项错误;
D.,此抛物线与 轴没有交点,所以D选项正确.
3. C
4. C
【解析】因为二次函数 的图象经过点 ,
所以方程 一定有一个解为:,
因为抛物线的对称轴为:直线 ,
所以二次函数 的图象与 轴的另一个交点为:,
所以方程 的解为:,.
5. B
【解析】若 ,则二次函数图象在一次函数图象的下面,此时 的取值范围是 .
6. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
7. A
【解析】由图象可知,抛物线与 轴的一个交点为 ,对称轴是 ,
根据抛物线的对称性可知抛物线与 轴的另一个交点的坐标为 .由图象看出当 时,函数图象在 轴上方,所以不等式 的解集是 .
8. A
【解析】根据题意得 ,
,
当 时,有 ,
,
,
②正确,
由 ,得 ,
,
,
①正确,
由 得 ,
当 时,,
而 ,,
,
③正确,
若方程 有两个不相等的实数根,
即 有两个不相等的实数根,
顶点的纵坐标 ,
,
④正确.
9. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
10. D
【解析】① 抛物线 (,, 是常数,)经过点 ,,
,,
,
当 时,与其对应的函数值 .
,
,
解得:,
,
,故①正确;
② ,,
,
即 ,
.
,
,
关于 的方程 有两个不等的实数根,故②正确;
③ ,,
.
,
,
.故③正确.
11.
12. 或
13.
【解析】由题意知二次函数 的两个相异的不动点 , 是方程 的两个不相等实数根,
且 ,
整理,得:,
由 有两个不相等的实数根,且 ,
知 ,
令 ,画出该二次函数的草图如下:
则
解得 .
14. ②③
15.
【解析】 二次函数 ,当 时,函数 有最小值 ,
当 时, 时取得最小值,,得 (舍去).
当 时, 时取得最小值,,得 (舍去),(舍去);
当 时, 时取得最小值,,得 .
由上可得, 的值是 .
16. (1) 当 时,,
解得 ,,
当 ,即 时,方程有两个相等的实数根;
当 ,即 时,方程有两个不相等的实数根,
不论 为何值,该函数的图象与 轴总有公共点.
(2) 当 时,,
点 的纵坐标为 ,
该函数的图象与 轴交于点 ,点 在 轴上方,
.
设 ,即 是 的二次函数,
当 时,.
抛物线开口向上,
当 或 时,.
的取值范围是 或 .
(3) ①当 时,图象经过一、二、四象限;
②当 或 时,图象经过一、三、四象限;
③当 时,图象经过三、四象限;
④当 时,图象经过一、二、三、四象限.
【解析】根据()()两问,可得:
①当 时,开口向上,与 轴交点的横坐标:,,此时图象经过一、二、四象限;
②当 或 时,开口向下,与 轴交点的横坐标:,,此时图象经过一、三、四象限;
③当 时,开口向下,与 轴交点的横坐标为 ,此时图象经过三、四象限;
④当 时,开口向下,与 轴交点的横坐标为:,,此时图象经过一、二、三、四象限.
17. (1) .
(2) .
18. (1)
,
.
抛物线与 轴有两个公共点.
(2) .
化简得 .
解得 ,或 .
,.
由 可得 .
.
.
解得 .
.
19. (1) 函数 的图象经过点 ,得
,
整理,得 ,
解得 ,,
函数 的表达式 ,化简,得 ;
函数 的表达式 化简,得 ,
综上所述:函数 的表达式 ;
(2) 当 时 ,
整理,得
,
解得 ,,
的图象与 轴的交点是 ,,
当 时,.即 ,
,
,
,
,
整理,得
,
,
解得 ,(舍去).
(3) 当 在对称轴的左侧(含顶点)时, 随 的增大而减小,
与 关于对称轴对称,
由 ,得 ;
当时 在对称轴的右侧时, 随 的增大而增大,
由 ,得 ,
综上所述:,所求 的取值范围 .
20. (1) ① ;② .
【解析】①如图 所示,
过点 ,作 于 ,
②同样可得图形 的面积 .
(2) ①如图 所示:
② ,,,,(答案不唯一)
【解析】②如图 所示,
小明的图形 的面积 ,
新图形 的面积 .
新得到的图形 的面积与小明的图形 的面积相等.
21. (1) 当 时,,
的值为 .
(2) 由()可知抛物线的表达式为 ,
当 时,;
当 时,.
,
.
22. .
一、选择题(共10小题)
1. 抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A. 有两个不同的实数根 B. 有两个相同的实数根
C. 没有实数根 D. 无法判定
2. 下列二次函数的图象与 轴没有交点的是
A. B. C. D.
3. 抛物线 的开口向上,与 轴的交点在 轴的负半轴,那么方程 的两实数根的积
A. 大于零 B. 等于零 C. 小于零 D. 以上都不对
4. 若二次函数 的图象经过点 ,则方程 的解为
A. , B. ,
C. , D. ,
5. 如图,已知二次函数 的图象与正比例函数 的图象交于点 ,与 轴交于点 ,若 ,则 的取值范围是
A. B. C. D. 或
6. 二次函数 的图象如图所示,现有以下结论:
():
();
(),
();
();
其中正确的结论有
A. 个 B. 个 C. 个 D. 个
7. 如图是二次函数 的部分图象,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 抛物线 (,, 为常数)开口向下且过点 ,,下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是
A. B. C. D.
9. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
10. 已知抛物线 (,, 是常数,)经过点 ,,当 时,与其对应的函数值 .有下列结论:① ;②关于 的方程 有两个不等的实数根;③ .其中,正确结论的个数是
A. B. C. D.
二、填空题(共5小题)
11. 下图是抛物线 和一次函数 的图象,观察图象写出 时, 的取值范围 .
12. 已知函数 ,若使 成立的 值恰好有 个,则 的值为 .
13. 对于一个函数,自变量 取 时,函数值 也等于 ,我们称 为这个函数的不动点.如果二次函数 有两个相异的不动点 ,,且 ,则 的取值范围是 .
14. 关于抛物线 ,给出下列结论:
①当 时,抛物线与直线 没有交点;
②若抛物线与 轴有两个交点,则其中一定有一个交点在点 与 之间;
③若抛物线的顶点在点 ,, 所围成的三角形区域内(包括边界),则 .其中正确结论的序号是 .
15. 已知二次函数 ( 为常数),当 时,函数 有最小值 ,则 的值为 .
三、解答题(共7小题)
16. 已知二次函数 ( 为常数,且 ).
(1)求证:不论 为何值,该函数的图象与 轴总有公共点;
(2)设该函数的图象与 轴交于点 ,若点 在 轴上方,求 的取值范围;
(3)该函数图象所过的象限随 的值变化而变化,直接写出函数图象所经过的象限及对应的 的取值范围.
17. 已知关于 的二次函数 的图象的顶点 和其上一点 的坐标,求这个二次函数的解析式.
(1),.
(2),.
18. 已知抛物线 ( 为常数,且 ).
(1)求证:抛物线与 轴有两个公共点;
(2)设抛物线与 轴的两个公共点分别为 ,( 在 左侧),与 轴的交点为 .当 时,求抛物线的表达式.
19. 在平面直角坐标系中,设二次函数 ,其中 .
(1)若函数 的图象经过点 ,求函数 的解析式;
(2)若抛物线与 轴的两交点坐标为 ,( 点在 点的左侧),与 轴的交点为 ,满足 时,求 的值.
(3)已知点 和 在函数 的图象上,若 ,求 的取值范围.
20. 在平面直角坐标系 中,已知点 ,,,,,,其中 ,,,,, 为正整数.顺次连接 ,,,,, 的折线与 轴, 轴围成的封闭图形记为图形 .小明在求图形 的面积时,过点 ,,, 作 轴的垂线,将图形 分成 个四边形,计算这些四边形面积的和,可以求出图形 的面积.
请你参考小明的思路,解决下面的问题.
(1)当 时,
①若 ,,,如图 ,则图形 的面积为 ;
②用含有 ,, 的式子表示图形 的面积为 .
(2)当 时,从 ,,,, 这 个正整数中任选 个不同的数作为 ,,,,.
①小明选择了 ,,,,,请在图 中画出此时的图形 ;
②在①的条件下,若小聪用剩下的 个数 ,,,, 作为 ,,,, 的取值,使新得到的图形 的面积与小明的图形 的面积相等,请直接写出这五个数的排序 (写出一组即可).
21. 已知抛物线 经过点 .
(1)求 的值;
(2)若点 , 在该抛物线上,试比较 , 的大小.
22. 若抛物线 与 轴有交点,求 的取值范围.
答案
1. A
2. D
【解析】A.,此抛物线与 轴有两个交点,所以A选项错误;
B.,此抛物线与 轴有两个交点,所以B选项错误;
C.,此抛物线与 轴有1个交点,所以C选项错误;
D.,此抛物线与 轴没有交点,所以D选项正确.
3. C
4. C
【解析】因为二次函数 的图象经过点 ,
所以方程 一定有一个解为:,
因为抛物线的对称轴为:直线 ,
所以二次函数 的图象与 轴的另一个交点为:,
所以方程 的解为:,.
5. B
【解析】若 ,则二次函数图象在一次函数图象的下面,此时 的取值范围是 .
6. C
【解析】() 函数开口向下,
,
对称轴在 轴的右边,
,
,故命题正确;
(),,,
,故命题正确;
() 当 时,,
,故命题错误;
() 当 时,,
,故命题正确;
() 抛物线与 轴于两个交点,
,故命题正确.
7. A
【解析】由图象可知,抛物线与 轴的一个交点为 ,对称轴是 ,
根据抛物线的对称性可知抛物线与 轴的另一个交点的坐标为 .由图象看出当 时,函数图象在 轴上方,所以不等式 的解集是 .
8. A
【解析】根据题意得 ,
,
当 时,有 ,
,
,
②正确,
由 ,得 ,
,
,
①正确,
由 得 ,
当 时,,
而 ,,
,
③正确,
若方程 有两个不相等的实数根,
即 有两个不相等的实数根,
顶点的纵坐标 ,
,
④正确.
9. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
10. D
【解析】① 抛物线 (,, 是常数,)经过点 ,,
,,
,
当 时,与其对应的函数值 .
,
,
解得:,
,
,故①正确;
② ,,
,
即 ,
.
,
,
关于 的方程 有两个不等的实数根,故②正确;
③ ,,
.
,
,
.故③正确.
11.
12. 或
13.
【解析】由题意知二次函数 的两个相异的不动点 , 是方程 的两个不相等实数根,
且 ,
整理,得:,
由 有两个不相等的实数根,且 ,
知 ,
令 ,画出该二次函数的草图如下:
则
解得 .
14. ②③
15.
【解析】 二次函数 ,当 时,函数 有最小值 ,
当 时, 时取得最小值,,得 (舍去).
当 时, 时取得最小值,,得 (舍去),(舍去);
当 时, 时取得最小值,,得 .
由上可得, 的值是 .
16. (1) 当 时,,
解得 ,,
当 ,即 时,方程有两个相等的实数根;
当 ,即 时,方程有两个不相等的实数根,
不论 为何值,该函数的图象与 轴总有公共点.
(2) 当 时,,
点 的纵坐标为 ,
该函数的图象与 轴交于点 ,点 在 轴上方,
.
设 ,即 是 的二次函数,
当 时,.
抛物线开口向上,
当 或 时,.
的取值范围是 或 .
(3) ①当 时,图象经过一、二、四象限;
②当 或 时,图象经过一、三、四象限;
③当 时,图象经过三、四象限;
④当 时,图象经过一、二、三、四象限.
【解析】根据()()两问,可得:
①当 时,开口向上,与 轴交点的横坐标:,,此时图象经过一、二、四象限;
②当 或 时,开口向下,与 轴交点的横坐标:,,此时图象经过一、三、四象限;
③当 时,开口向下,与 轴交点的横坐标为 ,此时图象经过三、四象限;
④当 时,开口向下,与 轴交点的横坐标为:,,此时图象经过一、二、三、四象限.
17. (1) .
(2) .
18. (1)
,
.
抛物线与 轴有两个公共点.
(2) .
化简得 .
解得 ,或 .
,.
由 可得 .
.
.
解得 .
.
19. (1) 函数 的图象经过点 ,得
,
整理,得 ,
解得 ,,
函数 的表达式 ,化简,得 ;
函数 的表达式 化简,得 ,
综上所述:函数 的表达式 ;
(2) 当 时 ,
整理,得
,
解得 ,,
的图象与 轴的交点是 ,,
当 时,.即 ,
,
,
,
,
整理,得
,
,
解得 ,(舍去).
(3) 当 在对称轴的左侧(含顶点)时, 随 的增大而减小,
与 关于对称轴对称,
由 ,得 ;
当时 在对称轴的右侧时, 随 的增大而增大,
由 ,得 ,
综上所述:,所求 的取值范围 .
20. (1) ① ;② .
【解析】①如图 所示,
过点 ,作 于 ,
②同样可得图形 的面积 .
(2) ①如图 所示:
② ,,,,(答案不唯一)
【解析】②如图 所示,
小明的图形 的面积 ,
新图形 的面积 .
新得到的图形 的面积与小明的图形 的面积相等.
21. (1) 当 时,,
的值为 .
(2) 由()可知抛物线的表达式为 ,
当 时,;
当 时,.
,
.
22. .
