(分层突破)高中数学人教A版(2019)选择性必修必修第一册1.1.2空间向量的数量积运算B(Word含解析)
文档属性
| 名称 | (分层突破)高中数学人教A版(2019)选择性必修必修第一册1.1.2空间向量的数量积运算B(Word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 00:00:00 | ||
图片预览




文档简介
2022年9月7日高中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,,、,则的值为( )
A. B.
C. D.
2.关于函数描述正确的是( )
A.最小正周期是 B.最大值是
C.一条对称轴是 D.一个对称中心是
3.如图,在平行六面体中,底面是边长为1的正方形,若,且,则的长为( )
A. B. C. D.
4.已知,则( )
A.2 B.-2 C.0 D.
5.已知 ∈(0,),2sin2α=cos2α+1,则sinα=
A. B.
C. D.
6.已知是长方体外接球的一条直径,点在长方体表面上运动,长方体的棱长分别是1,1,,则的取值范围为( )
A. B. C. D.
7.设函数在的图像大致如下图,则f(x)的最小正周期为( )
A. B.
C. D.
8.关于函数有下述四个结论:
①f(x)是偶函数 ②f(x)在区间(,)单调递增
③f(x)在有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
A.①②④ B.②④ C.①④ D.①③
二、多选题
9.已知四面体ABCD中,AB,AC,AD两两互相垂直,则下列结论中,一定成立的是( )
A.
B.
C.
D.
10.若是空间任意三个向量,,下列关系中,不成立的是( )
A. B.
C. D.
11.关于函数,下列叙述正确的是( )
A.是偶函数 B.在区间单调递增
C.的最大值为2 D.在有4个零点
12.摩天轮常被当作一个城市的地标性建筑,如深圳前海的“湾区之光”摩天轮,如图所示,某摩天轮最高点离地面高度128米,转盘直径为120米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针匀速旋转分钟,当时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为4米
B.若旋转分钟后,游客距离地面的高度为米,则
C.若在,时刻,游客距离地面的高度相等,则的最小值为30
D.,,使得游客在该时刻距离地面的高度均为90米
三、填空题
13.函数的最小正周期是____
14.若函数的最大值为2,则常数的一个取值为________.
15.在棱长为1的正四面体中,点满足,点满足,当最短时,_______.
16.已知函数的最大值为3,的图象与y轴的交点坐标为,其相邻两条对称轴间的距离为,则_____.
四、解答题
17.已知是空间向量,根据下列各条件分别求:
(1);
(2);
(3);
(4);
(5);
(6).
18.建设生态文明,是关系人民福祉,关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似的满足函数关系.
(1)求函数的表达式;
(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
19.已知函数
(1)求的最小正周期;
(2)讨论在区间上的单调性;
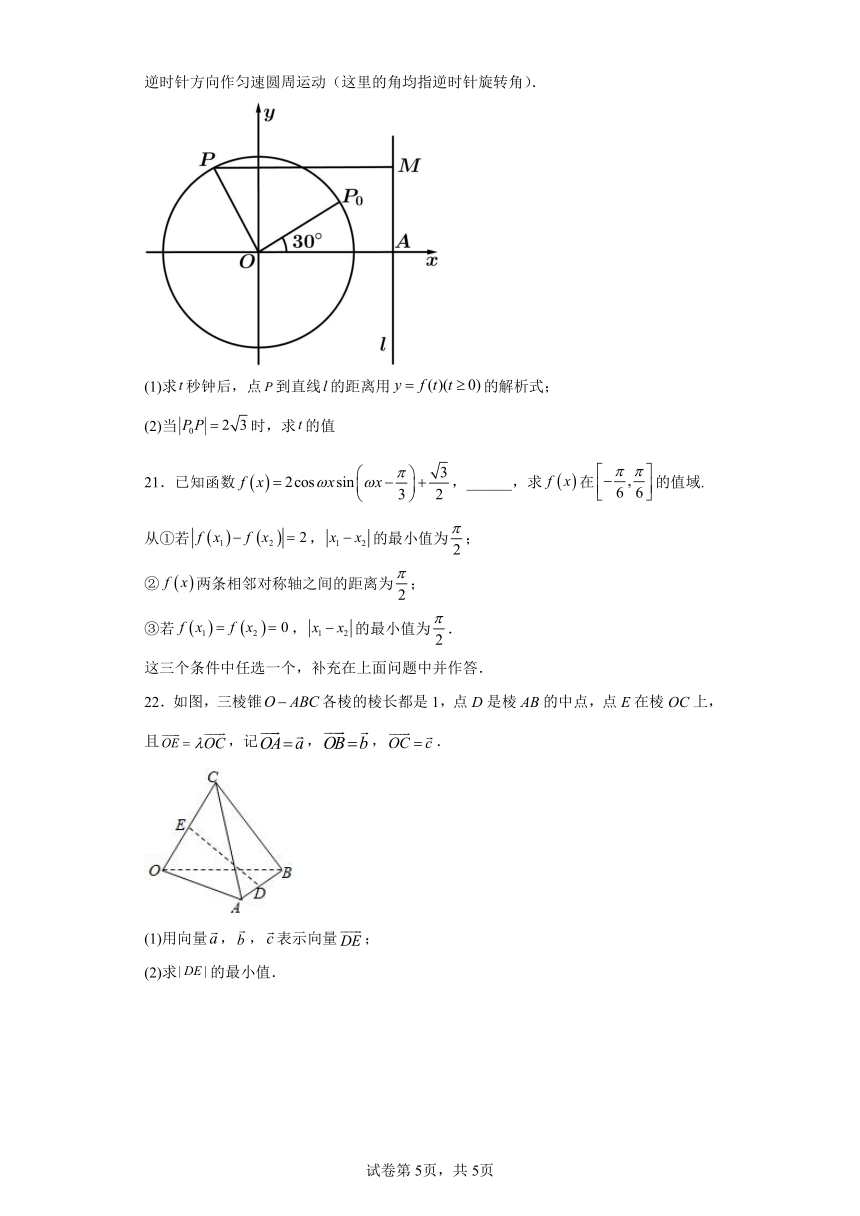
20.如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离.为圆周上一点,且.点从处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动(这里的角均指逆时针旋转角).
(1)求秒钟后,点到直线的距离用的解析式;
(2)当时,求的值
21.已知函数,______,求在的值域.
从①若,的最小值为;
②两条相邻对称轴之间的距离为;
③若,的最小值为.
这三个条件中任选一个,补充在上面问题中并作答.
22.如图,三棱锥各棱的棱长都是1,点D是棱AB的中点,点E在棱OC上,且,记,,.
(1)用向量,,表示向量;
(2)求的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A【分析】由、的范围求出的范围,由题意,利用平方关系求出和,由两角和与差的余弦公式求出的值即可.
【详解】解:、,,
,
,
.
.
.
故选:A.
【点睛】本题考查两角和与差的余弦公式,同角三角函数的基本关系的应用,属于基础题.
2.D【分析】利用三角恒等变换化简得解析式,再利用正弦型函数的图像和性质得出结论.
【详解】解:由题意得:
选项A:函数的最小正周期为,故A错误;
选项B:由于,函数的最大值为,故B错误;
选项C:函数的对称轴满足,,当时,,故C错误;
选项D:令,代入函数的,故为函数的一个对称中心,故D正确;
故选:D
3.C【分析】将作为基底,利用空间向量基本定理用基底表示,然后对其平方化简后,再开方可求得结果
【详解】由题意得,,
因为
,
所以
,
所以,
故选:C
4.B【分析】根据,利用诱导公式和商数关系求解.
【详解】因为,
所以,
,
,
故选:B
5.B【分析】利用二倍角公式得到正余弦关系,利用角范围及正余弦平方和为1关系得出答案.
【详解】,.
,又,,又,,故选B.
【点睛】本题为三角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦正负,运算准确性是关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负,很关键,切记不能凭感觉.
6.D【分析】先求得外接球的半径.
【详解】设外接球的半径为,则.
设是球心,则,
.
故选:D
7.C【分析】由图可得:函数图象过点,即可得到,结合是函数图象与轴负半轴的第一个交点即可得到,即可求得,再利用三角函数周期公式即可得解.
【详解】由图可得:函数图象过点,
将它代入函数可得:
又是函数图象与轴负半轴的第一个交点,
所以,解得:
所以函数的最小正周期为
故选:C
【点睛】本题主要考查了三角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.
8.C【分析】化简函数,研究它的性质从而得出正确答案.
【详解】为偶函数,故①正确.当时,,它在区间单调递减,故②错误.当时,,它有两个零点:;当时,,它有一个零点:,故在有个零点:,故③错误.当时,;当时,,又为偶函数,的最大值为,故④正确.综上所述,①④ 正确,故选C.
【点睛】画出函数的图象,由图象可得①④正确,故选C.
9.ABD【分析】根据题意在一个长方体内部作出四面体ABCD,从图形上把各个向量对应的有向线段表示出来,对四个选项进行判断即可.
【详解】由题可知,可做如图所示的长方体,设.
,
,故A正确;
,故B正确;
∵平面,∴,,∴,但无法判断AE和BC是否垂直,故C不一定正确;
由图易知,故=0,故D正确.
故选:ABD.
10.ABD【解析】根据空间向量加法法则、数量积的运算律、向量数乘法则和共线向量定理分别判断各选项.
【详解】由向量加法的平行四边形法则,只有,即时,都有,A不成立;
由数量积的运算律有,,与不一定相等,B不成立;
向量数乘法则,C一定成立;
只有共线且时,才存在,使得,D这成立.
故选:ABD.
11.AC【分析】根据函数的奇偶性、单调性、最值,零点等概念结合正弦函数性质判断各选项.
【详解】,是偶函数,A正确;
时,,单调递减,B错误;
,且,因此C正确;
在上,时,,
时,,
的零点只有共三个,D错.
故选:AC.
12.BC【分析】易知摩天轮离地面最近的距离,从而可判断A;求出分钟后,转过的角度,即可求出关于的表达式,即可判断B;由余弦型函数的性质可求出的最小值即可判断C;求出在上的单调性,结合当时,即可判断D.
【详解】解:由题意知,摩天轮离地面最近的距离为米,故A不正确;
分钟后,转过的角度为,则,B正确;
周期为,由余弦型函数的性质可知,若取最小值,
则,又高度相等,则关于对称,则,则;
令,解得,令,解得,
则在上单调递增,在上单调递减,当时,,
当时,,所以在只有一个解;
故选:BC.
【点睛】关键点睛:
本题的关键是求出关于的表达式,结合三角函数的性质进行判断.
13.1【分析】利用周期公式求解即可.
【详解】函数的最小正周期.
故答案为:1
14.(均可)【分析】根据两角和的正弦公式以及辅助角公式即可求得,可得,即可解出.
【详解】因为,
所以,解得,故可取.
故答案为:(均可).
【点睛】本题主要考查两角和的正弦公式,辅助角公式的应用,以及平方关系的应用,考查学生的数学运算能力,属于基础题.
15.【分析】根据题意得到面,,从而求得最短时,得到为的中心,为的中点,求得的长,结合,由向量的运算公式,即可求得的值.
【详解】解:因为,,
可得平面,,
当最短时,面,且,
所以为的中心,为的中点,如图所示,
又因为正四面体的棱长为,,
所以,
因为平面,所以,
因为,
所以
.
故答案为:.
16.【分析】利用二倍角公式可得,由函数的最大值可求出,由相邻两条对称轴间的距离可求出周期,再利用周期公式可求出,将点代入解析式可求出,从而可得函数的解析式,即可求出的值.
【详解】,
因为函数的最大值为,所以,所以,
由函数相邻两条对称轴间的距离为,可得周期,
所以,所以,
所以,又的图象与y轴的交点坐标为,
所以,所以,又,所以,
所以,
所以.
故答案为:
【点睛】本题主要考查求三角函数的图象与性质,二倍角的余弦公式,诱导公式,属于中档题.
17.(1)
(2)
(3)
(4)
(5)
(6)
【分析】利用向量夹角的范围,及余弦函数的单调性,由向量夹角的余弦值,分别求出(1)、(2)、(3)、(4)、(5)、(6)小题的角.
(1)
因为是空间向量,所以.
因为,所以.
(2)
因为是空间向量,所以.
因为,所以.
(3)
因为是空间向量,所以.
因为,所以.
(4)
因为是空间向量,所以.
因为,所以.
(5)
因为是空间向量,所以.
因为,所以.
(6)
因为是空间向量,所以.
因为,所以.
18.(1)(2)上午10时开启,下午18时关闭.【分析】(1)根据函数图象可知周期T,进而根据求得的值;结合函数的最大值和最小值,可求得A,代入最低点坐标,即可求得,进而得函数的解析式.
(2)根据题意,令,解不等式,结合t的取值范围即可求得开启和关闭中央空调时间.
【详解】(1)由图知,,
所以,得.
由图知,,,
所以.
将点代入函数解析式得,
得,即
又因为,得.
所以.
(2)依题意,令,
可得,
所以
解得:,
令得,,
故中央空调应在上午10时开启,下午18时关闭.
【点睛】本题考查了利用部分函数图象求三角函数解析式,三角函数在实际问题中的应用,属于基础题.
19.(1).(2)在区间上单调递增;在区间上单调递减.【分析】(1)根据题意,利用三角恒等变换化简为标准正弦型三角函数,利用最小正周期求解公式即可求得结果;
(2)先求得在上的单调增区间,结合区间,即可求得结果.
【详解】(1)依题意,
所以.
(2)依题意,令,,
解得,
所以的单调递增区间为,.
设,,易知,
所以当时,在区间上单调递增;
在区间上单调递减.
【点睛】本题考查利用三角恒等变换化简三角函数解析式,以及用公式法求正弦型三角函数的最小正周期,用整体法求正弦型三角函数的单调区间,属综合中档题.
20.(1)
(2)或.
【分析】(1)根据题意求出旋转角即可得出点的横坐标,即可求出解析式;
(2)可得当时,,即可求出.
(1)
由题意可得周期为,则秒钟后,旋转角为,
此时点的横坐标为,
所以点到直线的距离为;
(2)
当时,,
可得旋转了或,
解得或.
21.【分析】根据三个条件求得半周期,由此求得,进而求得在上的值域.
【详解】由于
.
所以,①②③任选一个作为条件,均可以得到的半周期为,则.
所以,.
由于,,
所以,即的值域为.
【点睛】本小题主要考查三角恒等变换,考查三角函数的周期、单调性、最值、值域的求法,属于中档题.
22.(1);(2).【分析】(1)根据题意,连接,,利用空间向量的线性运算即可求解;(2)由三棱锥的各个面是边长为1的正三角形可得、,再利用余弦定理求出,由空间向量的运算法则可得||2=||2,再结合空间向量的数量积公式和二次函数性质即可求解.
【详解】(1)根据题意,连接OD,CD,点D是棱AB的中点,点E在棱OC上,如下图:
由题意可得,,记,,,
∴()=.
(2)根据题意,点D是棱AB的中点,三棱锥的各个面是边长为1,
易得,,
在中,由余弦定理可得,,
,
当时,取得最小值,
则的最小值为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,,、,则的值为( )
A. B.
C. D.
2.关于函数描述正确的是( )
A.最小正周期是 B.最大值是
C.一条对称轴是 D.一个对称中心是
3.如图,在平行六面体中,底面是边长为1的正方形,若,且,则的长为( )
A. B. C. D.
4.已知,则( )
A.2 B.-2 C.0 D.
5.已知 ∈(0,),2sin2α=cos2α+1,则sinα=
A. B.
C. D.
6.已知是长方体外接球的一条直径,点在长方体表面上运动,长方体的棱长分别是1,1,,则的取值范围为( )
A. B. C. D.
7.设函数在的图像大致如下图,则f(x)的最小正周期为( )
A. B.
C. D.
8.关于函数有下述四个结论:
①f(x)是偶函数 ②f(x)在区间(,)单调递增
③f(x)在有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是
A.①②④ B.②④ C.①④ D.①③
二、多选题
9.已知四面体ABCD中,AB,AC,AD两两互相垂直,则下列结论中,一定成立的是( )
A.
B.
C.
D.
10.若是空间任意三个向量,,下列关系中,不成立的是( )
A. B.
C. D.
11.关于函数,下列叙述正确的是( )
A.是偶函数 B.在区间单调递增
C.的最大值为2 D.在有4个零点
12.摩天轮常被当作一个城市的地标性建筑,如深圳前海的“湾区之光”摩天轮,如图所示,某摩天轮最高点离地面高度128米,转盘直径为120米,设置若干个座舱,游客从离地面最近的位置进舱,开启后按逆时针匀速旋转分钟,当时,游客随舱旋转至距离地面最远处.以下关于摩天轮的说法中,正确的为( )
A.摩天轮离地面最近的距离为4米
B.若旋转分钟后,游客距离地面的高度为米,则
C.若在,时刻,游客距离地面的高度相等,则的最小值为30
D.,,使得游客在该时刻距离地面的高度均为90米
三、填空题
13.函数的最小正周期是____
14.若函数的最大值为2,则常数的一个取值为________.
15.在棱长为1的正四面体中,点满足,点满足,当最短时,_______.
16.已知函数的最大值为3,的图象与y轴的交点坐标为,其相邻两条对称轴间的距离为,则_____.
四、解答题
17.已知是空间向量,根据下列各条件分别求:
(1);
(2);
(3);
(4);
(5);
(6).
18.建设生态文明,是关系人民福祉,关乎民族未来的长远大计.某市通宵营业的大型商场,为响应节能减排的号召,在气温超过时,才开放中央空调降温,否则关闭中央空调.如图是该市夏季一天的气温(单位:)随时间(,单位:小时)的大致变化曲线,若该曲线近似的满足函数关系.
(1)求函数的表达式;
(2)请根据(1)的结论,判断该商场的中央空调应在本天内何时开启?何时关闭?
19.已知函数
(1)求的最小正周期;
(2)讨论在区间上的单调性;
20.如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离.为圆周上一点,且.点从处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动(这里的角均指逆时针旋转角).
(1)求秒钟后,点到直线的距离用的解析式;
(2)当时,求的值
21.已知函数,______,求在的值域.
从①若,的最小值为;
②两条相邻对称轴之间的距离为;
③若,的最小值为.
这三个条件中任选一个,补充在上面问题中并作答.
22.如图,三棱锥各棱的棱长都是1,点D是棱AB的中点,点E在棱OC上,且,记,,.
(1)用向量,,表示向量;
(2)求的最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A【分析】由、的范围求出的范围,由题意,利用平方关系求出和,由两角和与差的余弦公式求出的值即可.
【详解】解:、,,
,
,
.
.
.
故选:A.
【点睛】本题考查两角和与差的余弦公式,同角三角函数的基本关系的应用,属于基础题.
2.D【分析】利用三角恒等变换化简得解析式,再利用正弦型函数的图像和性质得出结论.
【详解】解:由题意得:
选项A:函数的最小正周期为,故A错误;
选项B:由于,函数的最大值为,故B错误;
选项C:函数的对称轴满足,,当时,,故C错误;
选项D:令,代入函数的,故为函数的一个对称中心,故D正确;
故选:D
3.C【分析】将作为基底,利用空间向量基本定理用基底表示,然后对其平方化简后,再开方可求得结果
【详解】由题意得,,
因为
,
所以
,
所以,
故选:C
4.B【分析】根据,利用诱导公式和商数关系求解.
【详解】因为,
所以,
,
,
故选:B
5.B【分析】利用二倍角公式得到正余弦关系,利用角范围及正余弦平方和为1关系得出答案.
【详解】,.
,又,,又,,故选B.
【点睛】本题为三角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦正负,运算准确性是关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负,很关键,切记不能凭感觉.
6.D【分析】先求得外接球的半径.
【详解】设外接球的半径为,则.
设是球心,则,
.
故选:D
7.C【分析】由图可得:函数图象过点,即可得到,结合是函数图象与轴负半轴的第一个交点即可得到,即可求得,再利用三角函数周期公式即可得解.
【详解】由图可得:函数图象过点,
将它代入函数可得:
又是函数图象与轴负半轴的第一个交点,
所以,解得:
所以函数的最小正周期为
故选:C
【点睛】本题主要考查了三角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.
8.C【分析】化简函数,研究它的性质从而得出正确答案.
【详解】为偶函数,故①正确.当时,,它在区间单调递减,故②错误.当时,,它有两个零点:;当时,,它有一个零点:,故在有个零点:,故③错误.当时,;当时,,又为偶函数,的最大值为,故④正确.综上所述,①④ 正确,故选C.
【点睛】画出函数的图象,由图象可得①④正确,故选C.
9.ABD【分析】根据题意在一个长方体内部作出四面体ABCD,从图形上把各个向量对应的有向线段表示出来,对四个选项进行判断即可.
【详解】由题可知,可做如图所示的长方体,设.
,
,故A正确;
,故B正确;
∵平面,∴,,∴,但无法判断AE和BC是否垂直,故C不一定正确;
由图易知,故=0,故D正确.
故选:ABD.
10.ABD【解析】根据空间向量加法法则、数量积的运算律、向量数乘法则和共线向量定理分别判断各选项.
【详解】由向量加法的平行四边形法则,只有,即时,都有,A不成立;
由数量积的运算律有,,与不一定相等,B不成立;
向量数乘法则,C一定成立;
只有共线且时,才存在,使得,D这成立.
故选:ABD.
11.AC【分析】根据函数的奇偶性、单调性、最值,零点等概念结合正弦函数性质判断各选项.
【详解】,是偶函数,A正确;
时,,单调递减,B错误;
,且,因此C正确;
在上,时,,
时,,
的零点只有共三个,D错.
故选:AC.
12.BC【分析】易知摩天轮离地面最近的距离,从而可判断A;求出分钟后,转过的角度,即可求出关于的表达式,即可判断B;由余弦型函数的性质可求出的最小值即可判断C;求出在上的单调性,结合当时,即可判断D.
【详解】解:由题意知,摩天轮离地面最近的距离为米,故A不正确;
分钟后,转过的角度为,则,B正确;
周期为,由余弦型函数的性质可知,若取最小值,
则,又高度相等,则关于对称,则,则;
令,解得,令,解得,
则在上单调递增,在上单调递减,当时,,
当时,,所以在只有一个解;
故选:BC.
【点睛】关键点睛:
本题的关键是求出关于的表达式,结合三角函数的性质进行判断.
13.1【分析】利用周期公式求解即可.
【详解】函数的最小正周期.
故答案为:1
14.(均可)【分析】根据两角和的正弦公式以及辅助角公式即可求得,可得,即可解出.
【详解】因为,
所以,解得,故可取.
故答案为:(均可).
【点睛】本题主要考查两角和的正弦公式,辅助角公式的应用,以及平方关系的应用,考查学生的数学运算能力,属于基础题.
15.【分析】根据题意得到面,,从而求得最短时,得到为的中心,为的中点,求得的长,结合,由向量的运算公式,即可求得的值.
【详解】解:因为,,
可得平面,,
当最短时,面,且,
所以为的中心,为的中点,如图所示,
又因为正四面体的棱长为,,
所以,
因为平面,所以,
因为,
所以
.
故答案为:.
16.【分析】利用二倍角公式可得,由函数的最大值可求出,由相邻两条对称轴间的距离可求出周期,再利用周期公式可求出,将点代入解析式可求出,从而可得函数的解析式,即可求出的值.
【详解】,
因为函数的最大值为,所以,所以,
由函数相邻两条对称轴间的距离为,可得周期,
所以,所以,
所以,又的图象与y轴的交点坐标为,
所以,所以,又,所以,
所以,
所以.
故答案为:
【点睛】本题主要考查求三角函数的图象与性质,二倍角的余弦公式,诱导公式,属于中档题.
17.(1)
(2)
(3)
(4)
(5)
(6)
【分析】利用向量夹角的范围,及余弦函数的单调性,由向量夹角的余弦值,分别求出(1)、(2)、(3)、(4)、(5)、(6)小题的角.
(1)
因为是空间向量,所以.
因为,所以.
(2)
因为是空间向量,所以.
因为,所以.
(3)
因为是空间向量,所以.
因为,所以.
(4)
因为是空间向量,所以.
因为,所以.
(5)
因为是空间向量,所以.
因为,所以.
(6)
因为是空间向量,所以.
因为,所以.
18.(1)(2)上午10时开启,下午18时关闭.【分析】(1)根据函数图象可知周期T,进而根据求得的值;结合函数的最大值和最小值,可求得A,代入最低点坐标,即可求得,进而得函数的解析式.
(2)根据题意,令,解不等式,结合t的取值范围即可求得开启和关闭中央空调时间.
【详解】(1)由图知,,
所以,得.
由图知,,,
所以.
将点代入函数解析式得,
得,即
又因为,得.
所以.
(2)依题意,令,
可得,
所以
解得:,
令得,,
故中央空调应在上午10时开启,下午18时关闭.
【点睛】本题考查了利用部分函数图象求三角函数解析式,三角函数在实际问题中的应用,属于基础题.
19.(1).(2)在区间上单调递增;在区间上单调递减.【分析】(1)根据题意,利用三角恒等变换化简为标准正弦型三角函数,利用最小正周期求解公式即可求得结果;
(2)先求得在上的单调增区间,结合区间,即可求得结果.
【详解】(1)依题意,
所以.
(2)依题意,令,,
解得,
所以的单调递增区间为,.
设,,易知,
所以当时,在区间上单调递增;
在区间上单调递减.
【点睛】本题考查利用三角恒等变换化简三角函数解析式,以及用公式法求正弦型三角函数的最小正周期,用整体法求正弦型三角函数的单调区间,属综合中档题.
20.(1)
(2)或.
【分析】(1)根据题意求出旋转角即可得出点的横坐标,即可求出解析式;
(2)可得当时,,即可求出.
(1)
由题意可得周期为,则秒钟后,旋转角为,
此时点的横坐标为,
所以点到直线的距离为;
(2)
当时,,
可得旋转了或,
解得或.
21.【分析】根据三个条件求得半周期,由此求得,进而求得在上的值域.
【详解】由于
.
所以,①②③任选一个作为条件,均可以得到的半周期为,则.
所以,.
由于,,
所以,即的值域为.
【点睛】本小题主要考查三角恒等变换,考查三角函数的周期、单调性、最值、值域的求法,属于中档题.
22.(1);(2).【分析】(1)根据题意,连接,,利用空间向量的线性运算即可求解;(2)由三棱锥的各个面是边长为1的正三角形可得、,再利用余弦定理求出,由空间向量的运算法则可得||2=||2,再结合空间向量的数量积公式和二次函数性质即可求解.
【详解】(1)根据题意,连接OD,CD,点D是棱AB的中点,点E在棱OC上,如下图:
由题意可得,,记,,,
∴()=.
(2)根据题意,点D是棱AB的中点,三棱锥的各个面是边长为1,
易得,,
在中,由余弦定理可得,,
,
当时,取得最小值,
则的最小值为.
答案第1页,共2页
答案第1页,共2页
