(分层突破)高中数学人教A版(2019)选择性必修必修第一册1.3.2空间向量运算的坐标表示A(Word含解析)
文档属性
| 名称 | (分层突破)高中数学人教A版(2019)选择性必修必修第一册1.3.2空间向量运算的坐标表示A(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 09:16:54 | ||
图片预览




文档简介
2022年9月7日高中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知空间向量,,则向量与()的夹角为( )
A. B.或 C. D.或
2.若向量,,则( )
A. B. C. D.
3.若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
4.对于任意空间向量 ,给出下列三个命题:①;②若,则为单位向量;③.其中真命题的个数为( )
A. B. C. D.
5.如图,为正方体的棱上一点,且,为棱上一点,且,则 ( )
A. B.2:6 C. D.
6.已知空间向量,,则下列结论不正确的是( )
A. B.
C. D.与夹角的余弦值为
二、多选题
7.已知向量,,则下列结论正确的是( )
A. B.
C. D.
8.已知,,,则下列结论正确的是( )
A. B.
C.为钝角 D.在方向上的投影向量为
三、填空题
9.若向量,且,则___________.
10.设空间向量,,若,则 ___.
11.已知空间向量,,,,1,,若与垂直,则等于
___________.
12.如图,棱长为2的正方体中,是棱的中点,点P在侧面内,若垂直于,则的面积的最小值为__________.
四、解答题
13.已知,,.求:
(1);
(2).
14.已知(2,3,﹣1),(﹣1,0,3),(0,1,2).
(1)求的值;
(2)已知,,||=||,求.
15.已知,,.
(1)若,求的值;
(2)若,求的值.
16.已知,.
(1)求;
(2)求与夹角的余弦值;
(3)求确定、的值使得与轴垂直,且.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B【解析】根据数量积运算,结合的正负,求解对应的两个夹角.
【详解】
解得,
代入得,又向量夹角范围:
故的夹角为,则与的夹角,
当时为;时为.
故选:B.
【点睛】本题考查空间向量的数量积,以及向量夹角的求解,属基础题.
2.C【分析】求出的坐标,利用空间向量的模长公式可求得结果.
【详解】由已知可得,故.
故选:C.
3.B【解析】根据坐标关系可知,再由是平面的法向量,是直线l的方向向量,即得.
【详解】由题得,,则,又是平面的法向量,是直线l的方向向量,可得.
故选:B
【点睛】本题考查直线和平面的位置关系,是基础题.
4.B【解析】由空间向量平行的条件可判断①;根据向量的模的计算可判断②;由空间向量垂直的条件可判断③,从而可得选项.
【详解】由可以推出,反之不一定成立,例:、,则,
故①不正确;
当时,,故②不正确;
当时,,即,反之也成立,故③正确.
所以正确命题的个数为:1.
故选:B.
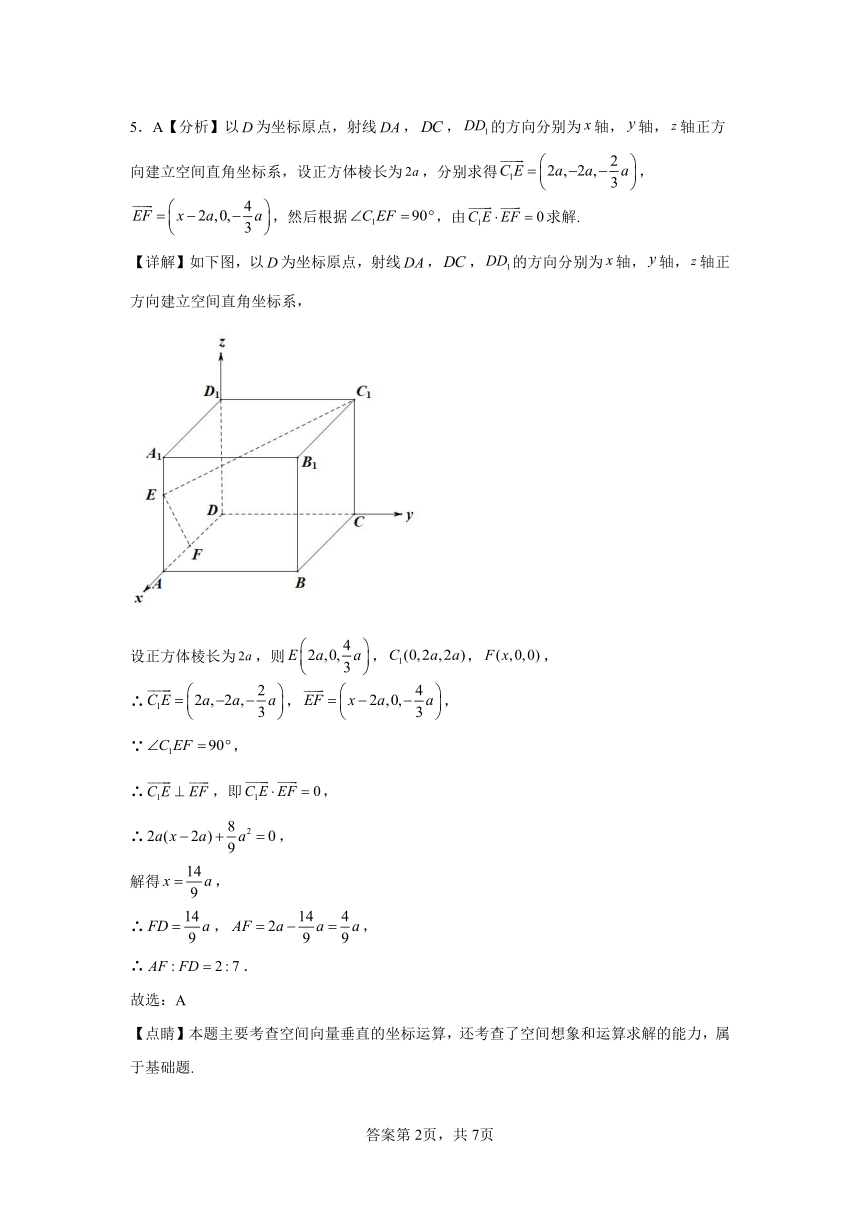
5.A【分析】以为坐标原点,射线,,的方向分别为轴,轴,轴正方向建立空间直角坐标系,设正方体棱长为,分别求得,,然后根据,由求解.
【详解】如下图,以为坐标原点,射线,,的方向分别为轴,轴,轴正方向建立空间直角坐标系,
设正方体棱长为,则,,,
∴,,
∵,
∴,即,
∴,
解得,
∴,,
∴.
故选:A
【点睛】本题主要考查空间向量垂直的坐标运算,还考查了空间想象和运算求解的能力,属于基础题.
6.A【分析】类比平面向量的计算办法,判断两向量是否平行可得,,故A错;
以及,故B正确;向量乘积为0即垂直,故C对;
用可判断D对.
【详解】因为,,而,故A不正确;
因为,,所以,故B正确;
因为,故C正确;
又,故D正确.
故选:A
7.AC【分析】根据空间向量加减法的坐标运算、空间向量的数量积的坐标表示、空间向量的模长公式计算可得结果.
【详解】因为,,
所以,故A正确;
,故B不正确;
,故C正确;
,故D不正确.
故选:AC
8.BD【分析】利用向量垂直,平行的坐标关系判断A,B,根据向量夹角公式判断C,根据投影向量和投影数量的关系计算求解判断D.
【详解】因为,所以,不垂直,A错,
因为,所以,B对,
因为,所以,所以不是钝角,C错,
因为在方向上的投影向量,D对,
故选:BD.
9.【分析】空间向量垂直,则空间向量的数量积为0,进而列出方程,求得结果
【详解】因为,所以,即,解得:
故答案为:
10.【分析】先利用空间向量共线的坐标表示列方程求出和的值,进而可得的坐标,再由模长公式即可求解.
【详解】因为空间向量,,且,
所以,
即,
可得,解得:,,
所以,,
则,
所以.
故答案为:.
11.【解析】利用向量垂直关系,与垂直,则,可求得,得到向量 ,进而求模长即可.
【详解】解:,,,,1,,
,,,
与垂直,
,
,
解得,,
,,
.
故答案为:.
12.【分析】建立空间直角坐标系,由,求得,得到,进而求得三角形的面积的最小值,得到答案.
【详解】以D点为空间直角坐标系的原点,以DC所在直线为y轴,以DA所在直线为x轴,以 为z轴,建立空间直角坐标系.则点,
所以.
因为,所以,
因为,所以,所以,
因为B(2,2,0),所以,
所以
因为,所以当时,.
因为BC⊥BP,所以.
故答案为:.
【点睛】本题主要考查了空间向量的应用,其中解答建立适当的空间直角坐标系,利用向量的坐标表示,以及向量的数量积的运算,求得的最小值是解答的关键,着重考查了推理与运算能力,属于中档试题.
13.(1)
(2)
【分析】(1)根据向量的加减运算法则,即可得;(2)根据数乘与向量的加减运算法则,即可得.
(1)
解:,
;
(2)
解:.
14.(1)-13;(2)(3,﹣2,1)或(﹣3,2,﹣1).【分析】(1)根据空间向量运算律进行计算即可;
(2)设(x,y,z),根据⊥,⊥,||=||列方程组可解决此问题.
【详解】(1)∵(2,3,﹣1),(﹣1,0,3),(0,1,2),
∴(﹣2,﹣3,0),
∴()=2×(﹣2)+3×(﹣3)+(﹣1)×0=﹣13;
(2)设(x,y,z),
∵⊥,⊥,||=||,
∴,
解得:或,
∴(3,﹣2,1)或(﹣3,2,﹣1).
15.(1)-6
(2)-4【解析】(1)利用向量共线的坐标表示,即得解;
(2)利用向量加法和向量垂直的坐标表示,即得解;
【详解】解:(1),
∴,
∴.
(2),
∵,
∴,
∴,
∴.
【点睛】本题考查了向量平行,加法,数量积的坐标表示,考查了学生概念理解,数学运算的能力,属于基础题.
16.(1);(2);(3),.【分析】(1)利用向量的数量积运算求解;
(2)利用向量的夹角公式求解;
(3)取轴上的单位向量,由与轴垂直,且,利用数量积运算求解.
【详解】(1)因为,,
所以.
(2)∵,,
∴,
∴与夹角的余弦值为,
(3)取轴上的单位向量,,
依题意,
即,
故,
解得,.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知空间向量,,则向量与()的夹角为( )
A. B.或 C. D.或
2.若向量,,则( )
A. B. C. D.
3.若直线l的方向向量为,平面的法向量为,则直线l与平面的位置关系是( )
A. B. C. D.l与斜交
4.对于任意空间向量 ,给出下列三个命题:①;②若,则为单位向量;③.其中真命题的个数为( )
A. B. C. D.
5.如图,为正方体的棱上一点,且,为棱上一点,且,则 ( )
A. B.2:6 C. D.
6.已知空间向量,,则下列结论不正确的是( )
A. B.
C. D.与夹角的余弦值为
二、多选题
7.已知向量,,则下列结论正确的是( )
A. B.
C. D.
8.已知,,,则下列结论正确的是( )
A. B.
C.为钝角 D.在方向上的投影向量为
三、填空题
9.若向量,且,则___________.
10.设空间向量,,若,则 ___.
11.已知空间向量,,,,1,,若与垂直,则等于
___________.
12.如图,棱长为2的正方体中,是棱的中点,点P在侧面内,若垂直于,则的面积的最小值为__________.
四、解答题
13.已知,,.求:
(1);
(2).
14.已知(2,3,﹣1),(﹣1,0,3),(0,1,2).
(1)求的值;
(2)已知,,||=||,求.
15.已知,,.
(1)若,求的值;
(2)若,求的值.
16.已知,.
(1)求;
(2)求与夹角的余弦值;
(3)求确定、的值使得与轴垂直,且.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B【解析】根据数量积运算,结合的正负,求解对应的两个夹角.
【详解】
解得,
代入得,又向量夹角范围:
故的夹角为,则与的夹角,
当时为;时为.
故选:B.
【点睛】本题考查空间向量的数量积,以及向量夹角的求解,属基础题.
2.C【分析】求出的坐标,利用空间向量的模长公式可求得结果.
【详解】由已知可得,故.
故选:C.
3.B【解析】根据坐标关系可知,再由是平面的法向量,是直线l的方向向量,即得.
【详解】由题得,,则,又是平面的法向量,是直线l的方向向量,可得.
故选:B
【点睛】本题考查直线和平面的位置关系,是基础题.
4.B【解析】由空间向量平行的条件可判断①;根据向量的模的计算可判断②;由空间向量垂直的条件可判断③,从而可得选项.
【详解】由可以推出,反之不一定成立,例:、,则,
故①不正确;
当时,,故②不正确;
当时,,即,反之也成立,故③正确.
所以正确命题的个数为:1.
故选:B.
5.A【分析】以为坐标原点,射线,,的方向分别为轴,轴,轴正方向建立空间直角坐标系,设正方体棱长为,分别求得,,然后根据,由求解.
【详解】如下图,以为坐标原点,射线,,的方向分别为轴,轴,轴正方向建立空间直角坐标系,
设正方体棱长为,则,,,
∴,,
∵,
∴,即,
∴,
解得,
∴,,
∴.
故选:A
【点睛】本题主要考查空间向量垂直的坐标运算,还考查了空间想象和运算求解的能力,属于基础题.
6.A【分析】类比平面向量的计算办法,判断两向量是否平行可得,,故A错;
以及,故B正确;向量乘积为0即垂直,故C对;
用可判断D对.
【详解】因为,,而,故A不正确;
因为,,所以,故B正确;
因为,故C正确;
又,故D正确.
故选:A
7.AC【分析】根据空间向量加减法的坐标运算、空间向量的数量积的坐标表示、空间向量的模长公式计算可得结果.
【详解】因为,,
所以,故A正确;
,故B不正确;
,故C正确;
,故D不正确.
故选:AC
8.BD【分析】利用向量垂直,平行的坐标关系判断A,B,根据向量夹角公式判断C,根据投影向量和投影数量的关系计算求解判断D.
【详解】因为,所以,不垂直,A错,
因为,所以,B对,
因为,所以,所以不是钝角,C错,
因为在方向上的投影向量,D对,
故选:BD.
9.【分析】空间向量垂直,则空间向量的数量积为0,进而列出方程,求得结果
【详解】因为,所以,即,解得:
故答案为:
10.【分析】先利用空间向量共线的坐标表示列方程求出和的值,进而可得的坐标,再由模长公式即可求解.
【详解】因为空间向量,,且,
所以,
即,
可得,解得:,,
所以,,
则,
所以.
故答案为:.
11.【解析】利用向量垂直关系,与垂直,则,可求得,得到向量 ,进而求模长即可.
【详解】解:,,,,1,,
,,,
与垂直,
,
,
解得,,
,,
.
故答案为:.
12.【分析】建立空间直角坐标系,由,求得,得到,进而求得三角形的面积的最小值,得到答案.
【详解】以D点为空间直角坐标系的原点,以DC所在直线为y轴,以DA所在直线为x轴,以 为z轴,建立空间直角坐标系.则点,
所以.
因为,所以,
因为,所以,所以,
因为B(2,2,0),所以,
所以
因为,所以当时,.
因为BC⊥BP,所以.
故答案为:.
【点睛】本题主要考查了空间向量的应用,其中解答建立适当的空间直角坐标系,利用向量的坐标表示,以及向量的数量积的运算,求得的最小值是解答的关键,着重考查了推理与运算能力,属于中档试题.
13.(1)
(2)
【分析】(1)根据向量的加减运算法则,即可得;(2)根据数乘与向量的加减运算法则,即可得.
(1)
解:,
;
(2)
解:.
14.(1)-13;(2)(3,﹣2,1)或(﹣3,2,﹣1).【分析】(1)根据空间向量运算律进行计算即可;
(2)设(x,y,z),根据⊥,⊥,||=||列方程组可解决此问题.
【详解】(1)∵(2,3,﹣1),(﹣1,0,3),(0,1,2),
∴(﹣2,﹣3,0),
∴()=2×(﹣2)+3×(﹣3)+(﹣1)×0=﹣13;
(2)设(x,y,z),
∵⊥,⊥,||=||,
∴,
解得:或,
∴(3,﹣2,1)或(﹣3,2,﹣1).
15.(1)-6
(2)-4【解析】(1)利用向量共线的坐标表示,即得解;
(2)利用向量加法和向量垂直的坐标表示,即得解;
【详解】解:(1),
∴,
∴.
(2),
∵,
∴,
∴,
∴.
【点睛】本题考查了向量平行,加法,数量积的坐标表示,考查了学生概念理解,数学运算的能力,属于基础题.
16.(1);(2);(3),.【分析】(1)利用向量的数量积运算求解;
(2)利用向量的夹角公式求解;
(3)取轴上的单位向量,由与轴垂直,且,利用数量积运算求解.
【详解】(1)因为,,
所以.
(2)∵,,
∴,
∴与夹角的余弦值为,
(3)取轴上的单位向量,,
依题意,
即,
故,
解得,.
答案第1页,共2页
答案第1页,共2页
