(分层突破)高中数学人教A版(2019)选择性必修必修第一册1.4.2用空间向量研究距离、夹角问题C(Word含解析)
文档属性
| 名称 | (分层突破)高中数学人教A版(2019)选择性必修必修第一册1.4.2用空间向量研究距离、夹角问题C(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 09:22:45 | ||
图片预览




文档简介
2022年9月7日高中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在三棱锥中,平面,,,,分别是棱,,的中点,,,则直线与平面所成角的正弦值为( )
A. B. C. D.
2.若O为坐标原点, =(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A. B.
C. D.
3.已知三棱锥中,,,则异面直线,所成角为( )
A. B. C. D.
4.在正方体中,E,F分别为棱AD,的中点,则异面直线EF与所成角的余弦值为( ).
A. B. C. D.
5.如图所示,在三棱柱中,底面,,,点,分别是棱,的中点,则直线与所成的角是( )
A. B. C. D.
6.在长方体中,,,则异面直线与所成角的余弦值为
A. B. C. D.
7.如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
8.如图,棱长为1的正方体中,M为线段上的动点(含端点),有下列结论
①平面平面
②三棱锥体积最大值为
③当M为AB1中点时,直线与直线所成的角的余弦值为
④直线与所成的角不可能是
其中正确的是( )
A.①②④ B.②③ C.①②③ D.①③④
二、多选题
9.已知空间中三点,,,则下列结论正确的有( )
A.
B.与共线的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
10.三棱锥中,平面与平面的法向量分别为、,若,,则二面角的大小可能为( )
A. B. C. D.
11.在长方体中, 分别为棱 的中点,,,则正确的选项是( )
A.异面直线与所成角的大小为60°
B.异面直线与所成角的大小为90°
C.点到平面的距离为
D.点到平面的距离为
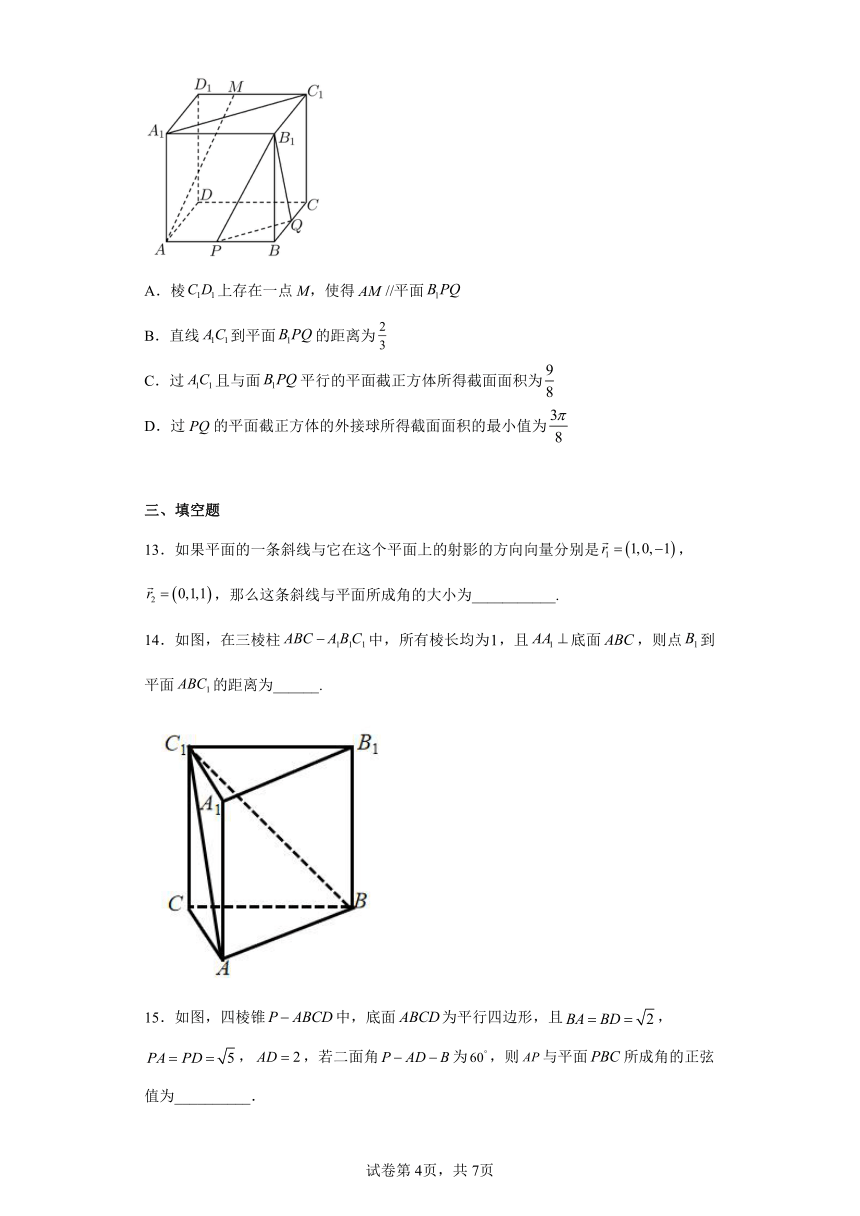
12.如图所示,在棱长为1的正方体中,P,Q分别为棱AB,BC的中点,则以下四个结论正确的是( )
A.棱上存在一点M,使得//平面
B.直线到平面的距离为
C.过且与面平行的平面截正方体所得截面面积为
D.过PQ的平面截正方体的外接球所得截面面积的最小值为
三、填空题
13.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是,,那么这条斜线与平面所成角的大小为___________.
14.如图,在三棱柱中,所有棱长均为,且底面,则点到平面的距离为______.
15.如图,四棱锥中,底面为平行四边形,且,,,若二面角为,则与平面所成角的正弦值为__________.
16.如图,在棱长为2的正方体中,分别是棱的中点,点在线段上运动,给出下列四个结论:
①平面截正方体所得的截面图形是五边形;
②直线到平面的距离是;
③存在点,使得;
④△面积的最小值是.
其中所有正确结论的序号是______.
四、解答题
17.如图,正方体中,是的中点,求与平面所成角的正弦值.
18.某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,分别是正方形的三边的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接就得到了一个“刍甍”(如图2).
(1)若是四边形对角线的交点,求证:∥平面
(2)若二面角的大小为,求直线与平面所成角的正弦值.
19.如图,在四棱锥中,、、两两垂直,,,,为线段上一点(端点除外).
(1)若异面直线、所成角的余弦值为,求的长;
(2)求二面角的平面角的余弦值.
20.如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
21.如图,在四棱锥中,四边形ABCD是矩形,△SAD是等边三角形,平面平面ABCD,AB=1,P为棱AD的中点,四棱锥的体积为.
(1)若E为棱SA的中点,F为棱SB的中点,求证:平面平面SCD.
(2)在棱SA上是否存在点M,使得平面PMB与平面SAD所成锐二面角的余弦值为?若存在,指出点M的位置;若不存在,请说明理由.
22.如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径,母线,M是PB的中点,四边形OBCH为正方形.
(1)设平面平面,证明:;
(2)设D为OH的中点,N是线段CD上的一个点,当MN与平面PAB所成角最大时,求MN的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B【分析】建立空间直角坐标系,利用空间向量夹角公式,结合线面角的定义进行求解即可.
【详解】因为,所以,因为平面,平面,
所以,以为空间直角坐标系的原点,以所在的直线为轴,建立如下图所示的空间直角坐标系,,
,,,
设平面的法向量为,
所以有,
设直线与平面所成角为,
所以,
故选:B
2.D【分析】先求出的坐标,再利用三角形减法法则求的坐标,再求||即得解.
【详解】由题意= (+)=,=-=,||=.
故答案为D
【点睛】本题主要考查向量的坐标运算,考查向量的三角形法则和平行四边形法则,考查向量的模的计算,意在考查学生对这些知识的掌握水平和分析推理能力.
3.B【分析】根据题意将图形补全成一个长、宽、高分别为1,1,的长方体,再利用向量法即可得出答案.
【详解】解:如图所示,在一个长、宽、高分别为1,1,的长方体中可以找到满足题意的三棱锥,以C为坐标原点,建立如图所示空间直角坐标系:
,,
,,
,
所以异面直线,所成角为.
故选:B.
4.A【分析】利用坐标法即得.
【详解】如图建立空间直角坐标系,设正方体的棱长为2,
则,
∴,
∴,
即异面直线EF与所成角的余弦值为.
故选:A.
5.C【分析】建立如图所示的空间直角坐标系,求出和的坐标,进而由夹角公式可求得结果.
【详解】如图所示,建立空间直角坐标系.由于,不妨取,则,,,,∴,,∴,又,∴,即直线与所成的角为.
故选:C.
6.C【详解】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与线线角相等或互补关系求结果.
详解:以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则,所以,
因为,所以异面直线与所成角的余弦值为,选C.
点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.
7.D【分析】设线段的中点为,连接,过点在平面内作,垂足为点,证明出平面,然后以点为坐标原点,、、分别为、、轴的正方向建立空间直角坐标系,设,其中,且,求出的最大值,利用空间向量法可求得的最大值.
【详解】设线段的中点为,连接,
,为的中点,则,
,则,,同理可得,,
,平面,
过点在平面内作,垂足为点,
因为,所以,为等边三角形,故为的中点,
平面,平面,则,
,,平面,
以点为坐标原点,、、分别为、、轴的正方向建立如下图所示的空间直角坐标系,
因为是边长为的等边三角形,为的中点,则,
则、、、,
由于点在平面内,
可设,
其中,且,
从而,
因为,则,
所以,,
故当时,有最大值,即,
故,即有最大值,
所以,.
故选:D.
【点睛】方法点睛:求空间角的常用方法:
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.
8.C【分析】利用面面垂直的判定定理可判断①,利用,可知三棱锥体积最大时,最大,由此可判断②,以为坐标原点建立空间直角坐标系,利用异面直线所成角的向量求法可判断③,假设,得到,假设所成角可以为,利用异面直线所成角的向量求法构造方程可求得的值,可判断④.
【详解】对于①,,,,平面,
平面,又平面,
平面平面,故①正确;
对于②,,
为上动点,当与重合时,取得最大值为,
,故②正确;
对于③,以为坐标原点,可建立如下图所示的空间直角坐标系,
当为中点时,,又,,,
,,
,
当为中点时,直线与直线所成的角的余弦值为,③正确;
对于④,设,,
又,,,
,则,,
,
,又,
,
若直线与所成的角为,则,
解得:,又,
当,即时,直线与所成的角为,故④错误.
所以其中正确的是①②③.
故选:C.
9.AD【分析】A选项,数量积为0,则两向量垂直;B选项,判断出不是单位向量,且与不共线;C选项,利用向量夹角坐标公式进行求解;D选项,利用数量积为0,证明出,从而得到结论.
【详解】,故,A正确;
不是单位向量,且与不共线,B错误;
,C错误;
设,则,,
所以,又,所以平面的一个法向量是,D正确.
故选:AD
10.AD【分析】求出的值,即可得解.
【详解】由已知可得,因此,二面角的大小为或.
故选:AD.
11.BC【分析】建立空间直角坐标系,求出,后,由可判断A、B;求出平面的一个法向量后,由点到平面的距离为可判断C、D.
【详解】如图建立空间直角坐标系,连接,
则,,,,,
所以,,
所以,所以,
所以异面直线与所成角的大小为90°,故A错误,B正确;
又,,
设平面的一个法向量,
则,令,则,
则点到平面的距离为,故C正确,D错误.
故选:BC.
【点睛】关键点点睛:
(1)建立合理的空间直角坐标系,利用空间向量求解异面直线的夹角;
(2)转化点到平面的距离为方向向量在平面法向量方向上投影的绝对值.
12.BCD【分析】建立空间直角坐标系,求出平面的法向量,借助空间向量分析计算可判断A,B;作出过与平面平行
的正方体截面,计算其面积判断C;求出直线PQ被正方体的外接球所截弦长即可计算作答.
【详解】在棱长为1的正方体中,建立如图所示的空间直角坐标系,
则,,
设平面的一个法向量,则,令,得,
设棱上点,,则,若//平面,则有,
解得,与矛盾,即在棱上不存在点M,使得//平面,A不正确;
连AC,矩形是正方体的对角面,有,而P,Q分别为棱AB,BC的中点,
则,又平面,平面,于是有平面,
直线到平面的距离等于点到平面的距离h,因,
则,B正确;
取AD,CD的中点E,F,连接,则,即确定一个平面,如图,
依题意,,,即四边形是平行四边形,,
平面,平面,于是得平面,
显然,平面,平面,于是得平面,
而,平面,因此,平面平面,
即梯形是过与平面平行的正方体的截面,
而,则此等腰梯形的高,
所以过与平面平行的正方体的截面面积为,C正确;
过PQ的平面截正方体的外接球所得截面小圆最小时,该小圆直径是直线PQ被正方体的外接球所截弦,
由对称性知线段PQ中点N是这个小圆的圆心,令正方体的外接球球心为O,连接ON,OP,
则,而,而球半径,
则这个小圆半径,此圆面积为,D正确.
故选:BCD
【点睛】关键点睛:几何体的外接球的表面积、体积计算问题,借助球的截面小圆性质确定出球心位置是解题的关键.
13.60°##【分析】利用向量数量积求出,从而求出,再根据斜线与平面夹角的概念即可求解.
【详解】∵,
∴,
又∵斜线和平面夹角的范围是,
∴这条斜线与平面所成角的大小为.
故答案为:60°.
14.【分析】以C为原点,分别为y、z轴正方向,建立空间直角坐标系,用向量法求解.
【详解】以C为原点,分别为y、z轴正方向,建立如图示的空间直角坐标系,
则,则,.设平面ABC1的一个法向量为,则有,不妨设z=1,解得,
则所求距离为
故答案为:.
15.【分析】取中点,连接,证明为二面角的平面角,所以,由余弦定理求得,得,由线面垂直判定定理和性质定理证明两两垂直,建立空间直角坐标系,用空间向量法求线面角.
【详解】取中点,连接,如图,则由已知得,,
所以为二面角的平面角,所以,
又,,
中,,,所以,
由,平面,得平面,
又平面,所以,
,平面,所以平面,
平面,所以,
,所以,
以为轴建立空间直角坐标系,如图,
则,,,
,平面的一个法向量是,
,
所以与平面所成角的正弦值为.
故答案为:.
16.①③【分析】作出截面图形判断①,利用等积法可判断②,利用坐标法可判断③④.
【详解】对于①,如图直线与、的延长线分别交于,连接分别交于,连接,
则五边形即为所得的截面图形,故①正确;
对于②,由题可知,平面,平面,
∴平面,故点到平面的距离即为直线到平面的距离,
设点到平面的距离为h,由正方体的棱长为2可得,
,,
∴,
,
∴由,可得,
所以直线到平面的距离是,故②错误;
对于③,如图建立空间直角坐标系,则,
设,
∴,又,
∴,,
假设存在点,使得,
∴,整理得,
∴(舍去)或,
故存在点,使得,故③正确;
对于④,由上知,所以点在的射影为,
∴点到的距离为:
,
∴当时,,
∴故△面积的最小值是,故④错误.
故答案为:①③.
17..【分析】建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
【详解】如图,建立空间直角坐标系,设正方体的棱长为2,则
.设平面的法向量为,
令,则,
.
故与平面所成角的正弦值为.
【点睛】本题考查了利用空间向量线面夹角公式的应用,考查了数学运算能力.
18.(1)证明见解析
(2)
【分析】(1)结合图形可证四边形是平行四边形,可得,可得∥平面;(2)根据题意结合二面角的定义可得,利用空间向量求线面夹角.
(1)
取线段中点,连接,由图1可知,四边形是矩形,且
是线段与的中点,且
在图1中且,且.
所以在图2中,且且
四边形是平行四边形,则
由于平面平面平面
(2)
由图1,折起后在图2中仍有
即为二面角的平面角.
以为坐标原点,分别为轴和轴正向建立空间直角坐标系如图,且设
则,
设平面的一个法向量
由,得,取则
于是平面的一个法向量
∴直线与平面所成角的正弦值为
19.(1);(2).【分析】(1)以、、所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设,,利用空间向量法结合异面直线、所成角的余弦值为可得出关于的方程,解出的值,即可求得的长;
(2)求出平面和平面的法向量,利用空间向量法可求得二面角的平面角的余弦值.
【详解】(1)因为、、两两垂直,所以以、、所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,
则由,,
得,,,,.
设,其中,
所以,
因为直线、所成角的余弦值为,
所以,
解得,所以,故的长为;
(2)由(1)知,,,.
设平面的一个法向量为.由,得.
取,则,所以平面的一个法向量为.
设平面的一个法向量为,由,得,
取,则,,所以平面的一个法向量为.
因为,
由图形可知,二面角的平面角为钝角,其余弦值为.
【点睛】本题考查利用异面直线所成角的余弦值求线段长度,同时也考查了利用空间向量法求二面角的余弦值,考查计算能力,属于中等题.
20.(I)证明见解析;(II);(III).【分析】(I)建立空间直角坐标系,求出及平面的一个法向量,证明,即可得证;
(II)求出,由运算即可得解;
(III)求得平面的一个法向量,由结合同角三角函数的平方关系即可得解.
【详解】(I)以为原点,分别为轴,建立如图空间直角坐标系,
则,,,,,,,
因为E为棱BC的中点,F为棱CD的中点,所以,,
所以,,,
设平面的一个法向量为,
则,令,则,
因为,所以,
因为平面,所以平面;
(II)由(1)得,,
设直线与平面所成角为,
则;
(III)由正方体的特征可得,平面的一个法向量为,
则,
所以二面角的正弦值为.
21.(1)证明见解析
(2)存在点M,位于AS的靠近点A的三等分点处
【分析】(1)由题可得EPSD,EFCD,即证;
(2)由题可得SP⊥平面ABCD,结合条件可得AD的长,建立空间直角坐标系,设=λ,利用条件列方程,即可解得.
(1)
因为E、F分别是SA、SB的中点,
所以EF AB,
在矩形ABCD中,AB CD,
所以EF CD,CD 平面SCD,EF平面SCD,
∴EF 平面SCD,
又因为E、P分别是SA、AD的中点,
所以EP SD,SD 平面SCD,EP平面SCD,
∴EP 平面SCD,
又EF∩EP=E,EF,EP平面PEF,
所以平面PEF 平面SCD.
(2)
假设在棱SA上存在点M满足题意,
在等边三角形SAD中,P为AD的中点,所以,
又平面平面ABCD,平面平面ABCD=AD,平面SAD,
所以平面ABCD,所以SP是四棱锥的高.
设,则,,
所以,所以m=2.
以点P为原点,,的方向分别为x,z轴的正方向,建立如图所示的空间直角坐标系,则,,,,
所以,,.
设,所以.
设平面PMB的一个法向量为,则,
所以取.易知平面SAD的一个法向量为,
所以,
因为,所以,
所以存在点M,位于AS的靠近点A的三等分点处满足题意.
22.(1)证明见解析
(2)
【分析】(1)根据线面平行的性质,先证明平面POH即可;
(2)以O为原点,OP所在的直线为z轴,建立空间直角坐标系,设,设MN与平面PAB所成的角为,再根据线面角的向量方法求得,根据二次函数的最值求解即可
(1)
因为四边形OBCH为正方形,∴,
∵平面POH,平面POH,∴平面POH.
∵平面PBC,平面平面,∴.
(2)
∵圆锥的母线长为,,∴,,
以O为原点,OP所在的直线为z轴,建立如图所示的空间直角坐标系,
则,,,,
设,,
,为平面PAB的一个法向量,
设MN与平面PAB所成的角为,
则,令,
则
所以当时,即时,最大,亦最大,此时,
所以.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在三棱锥中,平面,,,,分别是棱,,的中点,,,则直线与平面所成角的正弦值为( )
A. B. C. D.
2.若O为坐标原点, =(1,1,-2),=(3,2,8),=(0,1,0),则线段AB的中点P到点C的距离为( )
A. B.
C. D.
3.已知三棱锥中,,,则异面直线,所成角为( )
A. B. C. D.
4.在正方体中,E,F分别为棱AD,的中点,则异面直线EF与所成角的余弦值为( ).
A. B. C. D.
5.如图所示,在三棱柱中,底面,,,点,分别是棱,的中点,则直线与所成的角是( )
A. B. C. D.
6.在长方体中,,,则异面直线与所成角的余弦值为
A. B. C. D.
7.如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
8.如图,棱长为1的正方体中,M为线段上的动点(含端点),有下列结论
①平面平面
②三棱锥体积最大值为
③当M为AB1中点时,直线与直线所成的角的余弦值为
④直线与所成的角不可能是
其中正确的是( )
A.①②④ B.②③ C.①②③ D.①③④
二、多选题
9.已知空间中三点,,,则下列结论正确的有( )
A.
B.与共线的单位向量是
C.与夹角的余弦值是
D.平面的一个法向量是
10.三棱锥中,平面与平面的法向量分别为、,若,,则二面角的大小可能为( )
A. B. C. D.
11.在长方体中, 分别为棱 的中点,,,则正确的选项是( )
A.异面直线与所成角的大小为60°
B.异面直线与所成角的大小为90°
C.点到平面的距离为
D.点到平面的距离为
12.如图所示,在棱长为1的正方体中,P,Q分别为棱AB,BC的中点,则以下四个结论正确的是( )
A.棱上存在一点M,使得//平面
B.直线到平面的距离为
C.过且与面平行的平面截正方体所得截面面积为
D.过PQ的平面截正方体的外接球所得截面面积的最小值为
三、填空题
13.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是,,那么这条斜线与平面所成角的大小为___________.
14.如图,在三棱柱中,所有棱长均为,且底面,则点到平面的距离为______.
15.如图,四棱锥中,底面为平行四边形,且,,,若二面角为,则与平面所成角的正弦值为__________.
16.如图,在棱长为2的正方体中,分别是棱的中点,点在线段上运动,给出下列四个结论:
①平面截正方体所得的截面图形是五边形;
②直线到平面的距离是;
③存在点,使得;
④△面积的最小值是.
其中所有正确结论的序号是______.
四、解答题
17.如图,正方体中,是的中点,求与平面所成角的正弦值.
18.某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,分别是正方形的三边的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接就得到了一个“刍甍”(如图2).
(1)若是四边形对角线的交点,求证:∥平面
(2)若二面角的大小为,求直线与平面所成角的正弦值.
19.如图,在四棱锥中,、、两两垂直,,,,为线段上一点(端点除外).
(1)若异面直线、所成角的余弦值为,求的长;
(2)求二面角的平面角的余弦值.
20.如图,在棱长为2的正方体中,E为棱BC的中点,F为棱CD的中点.
(I)求证:平面;
(II)求直线与平面所成角的正弦值.
(III)求二面角的正弦值.
21.如图,在四棱锥中,四边形ABCD是矩形,△SAD是等边三角形,平面平面ABCD,AB=1,P为棱AD的中点,四棱锥的体积为.
(1)若E为棱SA的中点,F为棱SB的中点,求证:平面平面SCD.
(2)在棱SA上是否存在点M,使得平面PMB与平面SAD所成锐二面角的余弦值为?若存在,指出点M的位置;若不存在,请说明理由.
22.如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径,母线,M是PB的中点,四边形OBCH为正方形.
(1)设平面平面,证明:;
(2)设D为OH的中点,N是线段CD上的一个点,当MN与平面PAB所成角最大时,求MN的长.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B【分析】建立空间直角坐标系,利用空间向量夹角公式,结合线面角的定义进行求解即可.
【详解】因为,所以,因为平面,平面,
所以,以为空间直角坐标系的原点,以所在的直线为轴,建立如下图所示的空间直角坐标系,,
,,,
设平面的法向量为,
所以有,
设直线与平面所成角为,
所以,
故选:B
2.D【分析】先求出的坐标,再利用三角形减法法则求的坐标,再求||即得解.
【详解】由题意= (+)=,=-=,||=.
故答案为D
【点睛】本题主要考查向量的坐标运算,考查向量的三角形法则和平行四边形法则,考查向量的模的计算,意在考查学生对这些知识的掌握水平和分析推理能力.
3.B【分析】根据题意将图形补全成一个长、宽、高分别为1,1,的长方体,再利用向量法即可得出答案.
【详解】解:如图所示,在一个长、宽、高分别为1,1,的长方体中可以找到满足题意的三棱锥,以C为坐标原点,建立如图所示空间直角坐标系:
,,
,,
,
所以异面直线,所成角为.
故选:B.
4.A【分析】利用坐标法即得.
【详解】如图建立空间直角坐标系,设正方体的棱长为2,
则,
∴,
∴,
即异面直线EF与所成角的余弦值为.
故选:A.
5.C【分析】建立如图所示的空间直角坐标系,求出和的坐标,进而由夹角公式可求得结果.
【详解】如图所示,建立空间直角坐标系.由于,不妨取,则,,,,∴,,∴,又,∴,即直线与所成的角为.
故选:C.
6.C【详解】分析:先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角与线线角相等或互补关系求结果.
详解:以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则,所以,
因为,所以异面直线与所成角的余弦值为,选C.
点睛:利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.
7.D【分析】设线段的中点为,连接,过点在平面内作,垂足为点,证明出平面,然后以点为坐标原点,、、分别为、、轴的正方向建立空间直角坐标系,设,其中,且,求出的最大值,利用空间向量法可求得的最大值.
【详解】设线段的中点为,连接,
,为的中点,则,
,则,,同理可得,,
,平面,
过点在平面内作,垂足为点,
因为,所以,为等边三角形,故为的中点,
平面,平面,则,
,,平面,
以点为坐标原点,、、分别为、、轴的正方向建立如下图所示的空间直角坐标系,
因为是边长为的等边三角形,为的中点,则,
则、、、,
由于点在平面内,
可设,
其中,且,
从而,
因为,则,
所以,,
故当时,有最大值,即,
故,即有最大值,
所以,.
故选:D.
【点睛】方法点睛:求空间角的常用方法:
(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;
(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.
8.C【分析】利用面面垂直的判定定理可判断①,利用,可知三棱锥体积最大时,最大,由此可判断②,以为坐标原点建立空间直角坐标系,利用异面直线所成角的向量求法可判断③,假设,得到,假设所成角可以为,利用异面直线所成角的向量求法构造方程可求得的值,可判断④.
【详解】对于①,,,,平面,
平面,又平面,
平面平面,故①正确;
对于②,,
为上动点,当与重合时,取得最大值为,
,故②正确;
对于③,以为坐标原点,可建立如下图所示的空间直角坐标系,
当为中点时,,又,,,
,,
,
当为中点时,直线与直线所成的角的余弦值为,③正确;
对于④,设,,
又,,,
,则,,
,
,又,
,
若直线与所成的角为,则,
解得:,又,
当,即时,直线与所成的角为,故④错误.
所以其中正确的是①②③.
故选:C.
9.AD【分析】A选项,数量积为0,则两向量垂直;B选项,判断出不是单位向量,且与不共线;C选项,利用向量夹角坐标公式进行求解;D选项,利用数量积为0,证明出,从而得到结论.
【详解】,故,A正确;
不是单位向量,且与不共线,B错误;
,C错误;
设,则,,
所以,又,所以平面的一个法向量是,D正确.
故选:AD
10.AD【分析】求出的值,即可得解.
【详解】由已知可得,因此,二面角的大小为或.
故选:AD.
11.BC【分析】建立空间直角坐标系,求出,后,由可判断A、B;求出平面的一个法向量后,由点到平面的距离为可判断C、D.
【详解】如图建立空间直角坐标系,连接,
则,,,,,
所以,,
所以,所以,
所以异面直线与所成角的大小为90°,故A错误,B正确;
又,,
设平面的一个法向量,
则,令,则,
则点到平面的距离为,故C正确,D错误.
故选:BC.
【点睛】关键点点睛:
(1)建立合理的空间直角坐标系,利用空间向量求解异面直线的夹角;
(2)转化点到平面的距离为方向向量在平面法向量方向上投影的绝对值.
12.BCD【分析】建立空间直角坐标系,求出平面的法向量,借助空间向量分析计算可判断A,B;作出过与平面平行
的正方体截面,计算其面积判断C;求出直线PQ被正方体的外接球所截弦长即可计算作答.
【详解】在棱长为1的正方体中,建立如图所示的空间直角坐标系,
则,,
设平面的一个法向量,则,令,得,
设棱上点,,则,若//平面,则有,
解得,与矛盾,即在棱上不存在点M,使得//平面,A不正确;
连AC,矩形是正方体的对角面,有,而P,Q分别为棱AB,BC的中点,
则,又平面,平面,于是有平面,
直线到平面的距离等于点到平面的距离h,因,
则,B正确;
取AD,CD的中点E,F,连接,则,即确定一个平面,如图,
依题意,,,即四边形是平行四边形,,
平面,平面,于是得平面,
显然,平面,平面,于是得平面,
而,平面,因此,平面平面,
即梯形是过与平面平行的正方体的截面,
而,则此等腰梯形的高,
所以过与平面平行的正方体的截面面积为,C正确;
过PQ的平面截正方体的外接球所得截面小圆最小时,该小圆直径是直线PQ被正方体的外接球所截弦,
由对称性知线段PQ中点N是这个小圆的圆心,令正方体的外接球球心为O,连接ON,OP,
则,而,而球半径,
则这个小圆半径,此圆面积为,D正确.
故选:BCD
【点睛】关键点睛:几何体的外接球的表面积、体积计算问题,借助球的截面小圆性质确定出球心位置是解题的关键.
13.60°##【分析】利用向量数量积求出,从而求出,再根据斜线与平面夹角的概念即可求解.
【详解】∵,
∴,
又∵斜线和平面夹角的范围是,
∴这条斜线与平面所成角的大小为.
故答案为:60°.
14.【分析】以C为原点,分别为y、z轴正方向,建立空间直角坐标系,用向量法求解.
【详解】以C为原点,分别为y、z轴正方向,建立如图示的空间直角坐标系,
则,则,.设平面ABC1的一个法向量为,则有,不妨设z=1,解得,
则所求距离为
故答案为:.
15.【分析】取中点,连接,证明为二面角的平面角,所以,由余弦定理求得,得,由线面垂直判定定理和性质定理证明两两垂直,建立空间直角坐标系,用空间向量法求线面角.
【详解】取中点,连接,如图,则由已知得,,
所以为二面角的平面角,所以,
又,,
中,,,所以,
由,平面,得平面,
又平面,所以,
,平面,所以平面,
平面,所以,
,所以,
以为轴建立空间直角坐标系,如图,
则,,,
,平面的一个法向量是,
,
所以与平面所成角的正弦值为.
故答案为:.
16.①③【分析】作出截面图形判断①,利用等积法可判断②,利用坐标法可判断③④.
【详解】对于①,如图直线与、的延长线分别交于,连接分别交于,连接,
则五边形即为所得的截面图形,故①正确;
对于②,由题可知,平面,平面,
∴平面,故点到平面的距离即为直线到平面的距离,
设点到平面的距离为h,由正方体的棱长为2可得,
,,
∴,
,
∴由,可得,
所以直线到平面的距离是,故②错误;
对于③,如图建立空间直角坐标系,则,
设,
∴,又,
∴,,
假设存在点,使得,
∴,整理得,
∴(舍去)或,
故存在点,使得,故③正确;
对于④,由上知,所以点在的射影为,
∴点到的距离为:
,
∴当时,,
∴故△面积的最小值是,故④错误.
故答案为:①③.
17..【分析】建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
【详解】如图,建立空间直角坐标系,设正方体的棱长为2,则
.设平面的法向量为,
令,则,
.
故与平面所成角的正弦值为.
【点睛】本题考查了利用空间向量线面夹角公式的应用,考查了数学运算能力.
18.(1)证明见解析
(2)
【分析】(1)结合图形可证四边形是平行四边形,可得,可得∥平面;(2)根据题意结合二面角的定义可得,利用空间向量求线面夹角.
(1)
取线段中点,连接,由图1可知,四边形是矩形,且
是线段与的中点,且
在图1中且,且.
所以在图2中,且且
四边形是平行四边形,则
由于平面平面平面
(2)
由图1,折起后在图2中仍有
即为二面角的平面角.
以为坐标原点,分别为轴和轴正向建立空间直角坐标系如图,且设
则,
设平面的一个法向量
由,得,取则
于是平面的一个法向量
∴直线与平面所成角的正弦值为
19.(1);(2).【分析】(1)以、、所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,设,,利用空间向量法结合异面直线、所成角的余弦值为可得出关于的方程,解出的值,即可求得的长;
(2)求出平面和平面的法向量,利用空间向量法可求得二面角的平面角的余弦值.
【详解】(1)因为、、两两垂直,所以以、、所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,
则由,,
得,,,,.
设,其中,
所以,
因为直线、所成角的余弦值为,
所以,
解得,所以,故的长为;
(2)由(1)知,,,.
设平面的一个法向量为.由,得.
取,则,所以平面的一个法向量为.
设平面的一个法向量为,由,得,
取,则,,所以平面的一个法向量为.
因为,
由图形可知,二面角的平面角为钝角,其余弦值为.
【点睛】本题考查利用异面直线所成角的余弦值求线段长度,同时也考查了利用空间向量法求二面角的余弦值,考查计算能力,属于中等题.
20.(I)证明见解析;(II);(III).【分析】(I)建立空间直角坐标系,求出及平面的一个法向量,证明,即可得证;
(II)求出,由运算即可得解;
(III)求得平面的一个法向量,由结合同角三角函数的平方关系即可得解.
【详解】(I)以为原点,分别为轴,建立如图空间直角坐标系,
则,,,,,,,
因为E为棱BC的中点,F为棱CD的中点,所以,,
所以,,,
设平面的一个法向量为,
则,令,则,
因为,所以,
因为平面,所以平面;
(II)由(1)得,,
设直线与平面所成角为,
则;
(III)由正方体的特征可得,平面的一个法向量为,
则,
所以二面角的正弦值为.
21.(1)证明见解析
(2)存在点M,位于AS的靠近点A的三等分点处
【分析】(1)由题可得EPSD,EFCD,即证;
(2)由题可得SP⊥平面ABCD,结合条件可得AD的长,建立空间直角坐标系,设=λ,利用条件列方程,即可解得.
(1)
因为E、F分别是SA、SB的中点,
所以EF AB,
在矩形ABCD中,AB CD,
所以EF CD,CD 平面SCD,EF平面SCD,
∴EF 平面SCD,
又因为E、P分别是SA、AD的中点,
所以EP SD,SD 平面SCD,EP平面SCD,
∴EP 平面SCD,
又EF∩EP=E,EF,EP平面PEF,
所以平面PEF 平面SCD.
(2)
假设在棱SA上存在点M满足题意,
在等边三角形SAD中,P为AD的中点,所以,
又平面平面ABCD,平面平面ABCD=AD,平面SAD,
所以平面ABCD,所以SP是四棱锥的高.
设,则,,
所以,所以m=2.
以点P为原点,,的方向分别为x,z轴的正方向,建立如图所示的空间直角坐标系,则,,,,
所以,,.
设,所以.
设平面PMB的一个法向量为,则,
所以取.易知平面SAD的一个法向量为,
所以,
因为,所以,
所以存在点M,位于AS的靠近点A的三等分点处满足题意.
22.(1)证明见解析
(2)
【分析】(1)根据线面平行的性质,先证明平面POH即可;
(2)以O为原点,OP所在的直线为z轴,建立空间直角坐标系,设,设MN与平面PAB所成的角为,再根据线面角的向量方法求得,根据二次函数的最值求解即可
(1)
因为四边形OBCH为正方形,∴,
∵平面POH,平面POH,∴平面POH.
∵平面PBC,平面平面,∴.
(2)
∵圆锥的母线长为,,∴,,
以O为原点,OP所在的直线为z轴,建立如图所示的空间直角坐标系,
则,,,,
设,,
,为平面PAB的一个法向量,
设MN与平面PAB所成的角为,
则,令,
则
所以当时,即时,最大,亦最大,此时,
所以.
答案第1页,共2页
答案第1页,共2页
