高中数学人教A版(2019)必修第一册5.7三角函数的应用A(word含解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册5.7三角函数的应用A(word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 935.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 12:24:45 | ||
图片预览



文档简介
2022年9月7日高中数学作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
2.为了得到函数的图象,只需把余弦函数曲线上所有的点( )
A.向左平行移动个单位长度 B.向右平行移动个单位长度
C.向左平行移动个单位长度 D.向右平行移动个单位长度
3.达·芬奇的经典之作《蒙娜丽莎》举世闻名.如图,画中女子神秘的微笑,,数百年来让无数观赏者人迷.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行了粗略测绘,将画中女子的嘴唇近似看作一个圆弧,在嘴角处作圆弧的切线,两条切线交于点,测得如下数据:(其中).根据测量得到的结果推算:将《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角大约等于( )
A. B. C. D.
4.电流强度随时间变化的关系式是,则当时,电流强度为
A.5A B.2.5A C.2A D.-5A
5.已知某摩天轮的旋转半径为60米,最高点距地面135米,运行一周大约30分钟,某游客在最低点的位置坐上摩天轮,则第10分钟时他距地面大约为( )
A.95米 B.100米 C.105米 D.110米
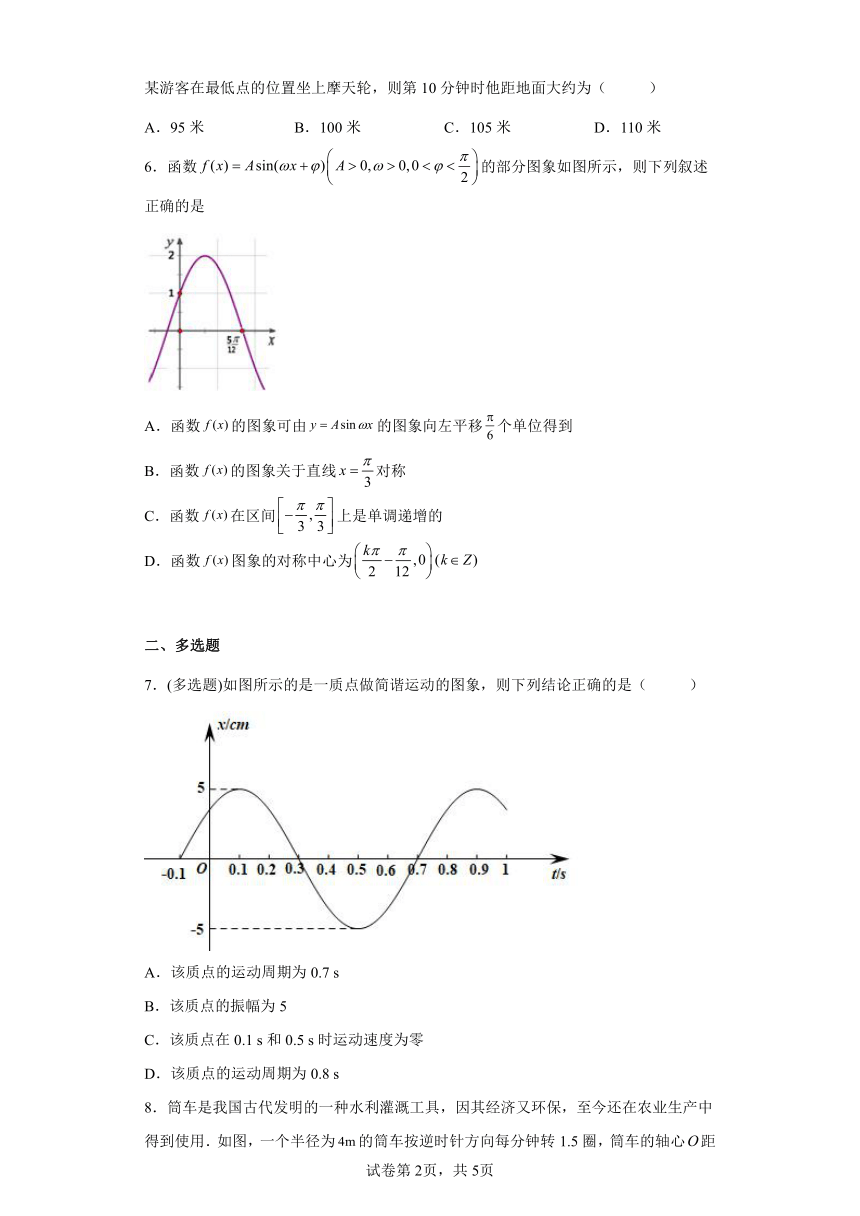
6.函数的部分图象如图所示,则下列叙述正确的是
A.函数的图象可由的图象向左平移个单位得到
B.函数的图象关于直线对称
C.函数在区间上是单调递增的
D.函数图象的对称中心为
二、多选题
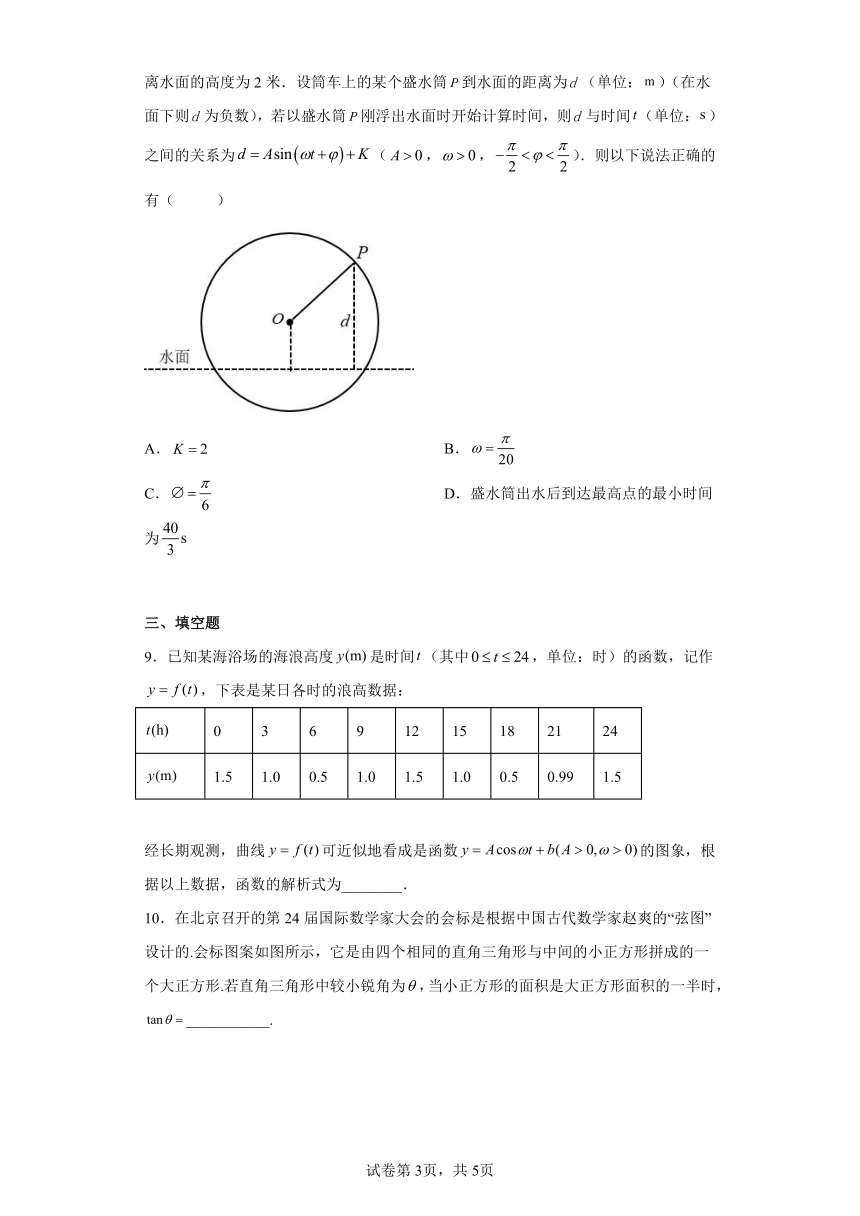
7.(多选题)如图所示的是一质点做简谐运动的图象,则下列结论正确的是( )
A.该质点的运动周期为0.7 s
B.该质点的振幅为5
C.该质点在0.1 s和0.5 s时运动速度为零
D.该质点的运动周期为0.8 s
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.如图,一个半径为的筒车按逆时针方向每分钟转1.5圈,筒车的轴心距离水面的高度为2米.设筒车上的某个盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计算时间,则与时间(单位:)之间的关系为(,,).则以下说法正确的有( )
A. B.
C. D.盛水筒出水后到达最高点的最小时间为
三、填空题
9.已知某海浴场的海浪高度是时间(其中,单位:时)的函数,记作,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,曲线可近似地看成是函数的图象,根据以上数据,函数的解析式为________.
10.在北京召开的第24届国际数学家大会的会标是根据中国古代数学家赵爽的“弦图”设计的.会标图案如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小锐角为,当小正方形的面积是大正方形面积的一半时,___________.
11.已知定义在R上的函数不是常数函数,写出一个同时具有下列三个性质的一个函数___________.
①;②;③.
12.筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时120秒,当时,盛水筒M位于点,经过t秒后运动到点,点P的纵坐标满足,则当筒车旋转100秒时,盛水筒M对应的点P的纵坐标为____________.
四、解答题
13.已知函数.
(1)求函数的最小正周期;
(2)求函数的最小值及相应的值.
14.已知,.
(1)求,的值;
(2)求的值.
15.2020年一场突如其来的疫情让亿万中华儿女的心再一次凝结在一起,为控制疫情,让广大发热患者得到及时有效的治疗,武汉市某社区决定临时修建一个医院.医院设计平面图如图所示:矩形中,米,米,图中区域为诊断区(、分别在和边上),、及区域为治疗区.受诊断区医疗设备的实际尺寸影响,要求的大小为.
(1)若按照米的方案修建医院,问诊断区是否符合要求?
(2)按照疫情现状,病人仍在不断增加,因此需要治疗区的面积尽可能的大,以便于增加床位,请给出具体的修建方案使得治疗区面积最大,并求出最大值.
16.已知函数,其图像过点.
(1)求φ的值;
(2)将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像,求函数在上的最大值和最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C【分析】由图中最小值求出,从而可得最大值.
【详解】由题干图易得ymin=k-3=2,则k=5.
∴ymax=k+3=8.
故选:C
【点睛】本题考查()的性质,的最大值为,最小值为.
2.C【解析】根据三角函数图象变换规律确定选项.
【详解】因为向左平行移动个单位长度得,
故选:C
【点睛】本题考查三角函数图象变换,考查基本分析判断能力,属基础题.
3.A【解析】由已知,设.可得.于是可得,进而得出结论.
【详解】解:依题意,设.
则.
,.
设《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角为.
则,
.
故选:A.
【点睛】本题考查了直角三角形的边角关系、三角函数的单调性、切线的性质,考查了推理能力与计算能力,属于中档题.
4.B【分析】由已知直接把代入,利用诱导公式及特殊角的三角函数值即可求出.
【详解】解:当时,.
故选:.
【点睛】本题考查三角函数的简单应用,属于基础题.
5.C【分析】设函数关系式为,根据题意求得各参数得解析式,然后计算可得.
【详解】设该游客在摩天轮上离地面高度(米)与时间t(分钟)的函数关系为,
由题意可知,,,所以,即.
又,得,故,
所以,
所以.
故选:C.
6.D【解析】根据题意求出解析式,利用正弦函数的对称性及单调性依次判断选项.
【详解】由图象可知A=2,f(0)=1,
∵f(0)=2sinφ=1,且,
∴,
∴f(x)=2sin(ωx),
∵f()=0且为单调递减时的零点,
∴,k∈Z,
∴,k∈Z,
由图象知,
∴ω,
又∵ω>0,
∴ω=2,
∴f(x)=2sin(2x),
∵函数f(x)的图象可由y=Asinωx的图象向左平移个单位得,
∴A错,
令2x,k∈Z,对称轴为x,则B错,
令2x,则x,则C错,
令2xkπ,k∈Z,则x=,则D对,
故选:D.
【点睛】本题考查三角函数图象及其性质,考查了正弦函数的对称性及单调性,属于中档题.
7.BCD【分析】由题图求得质点的振动周期可判定A错,D正确;由该质点的振幅,可判定B正确;由简谐运动的特点,可判定C正确.
【详解】由题图可知,质点的振动周期为2×(0.7-0.3)=0.8 s,所以A错,D正确;
该质点的振幅为5,所以B正确;
由简谐运动的特点知,质点处于平衡位置时的速度最大,即在0.3 s和0.7 s时运动速度最大,在0.1 s和0.5 s时运动速度为零,故C正确.
综上,BCD正确.
故选:BCD.
8.ABD【分析】由已知可得的值,得到函数解析式,取求得t的值,从而得解.
【详解】解:∵筒车按逆时针方向每分钟转1.5圈,,
则,故B正确;
振幅A为筒车的半径,即,故A正确;
由题意,t=0时,d=0,,即 ,
,∴,故C错误;
,
由d=6,得,
得
∴当k=0时,t取最小值为,故D正确.
故选:ABD.
9.【分析】由表中的数据可知,函数的最大值为1.5,最小值为0.5,从而可求出的值,再由表中的数据可得其最小正周期为12,从而可求出的值.
【详解】解:由题意得,,,
∴,.
又,∴.
从而.
故答案为:
【点睛】此题考查了三角函数模型的应用,掌握五点法是解题的关键,属于基础题.
10.【解析】设直角三角形直角边为,,令小正方形的面积为1,列方程组计算,,再根据锐角三角函数计算可得;.
【详解】解:设直角三角形中较长的直角边为,较短的直角边为,令小正方形的面积为1,则大正方形的面积为2,
则,解得或(舍去),
所以.
故答案为:.
11.(形式不唯一)【分析】由联想得到,可设,由周期性确定,猜想的值代入检验可确定.
【详解】解:由,
得,
联想到,
可推测.
由,
得,
则,
设,
则,所以满足题意.
故答案为:.(不唯一)
12.【分析】根据筒车按逆时针方向每旋转一周用时120秒,可求出,由时,求出和,从而可求出的关系式,进而可求出点P的纵坐标
【详解】因为筒车按逆时针方向每旋转一周用时120秒,
所以,得,
所以,
因为当时,盛水筒M位于点,
所以,
所以,
因为,
所以,得,
因为,所以,
所以,
所以,
所以当筒车旋转100秒时,盛水筒M对应的点P的纵坐标为,
故答案为:
13.(1)(2)的最小值为,此时.【分析】通过倍角公式,把化成标准形式,研究函数的相关性质(周期性,单调性,奇偶性,对称性,最值及最值相对于的变量),从而本题能顺利完成
【详解】(1)因为.
所以函数的最小正周期为.
(2)当时,,
此时,,,
所以的最小值为,此时.
【点睛】该类型考题关键是将化成性质,只有这样,我们才能很好的去研究他的性质.
14.(1),;(2)【分析】(1)首先利用同角三角函数关系求出,从而得到,再利用正弦二倍角公式计算即可.
(2)利用正弦两角差公式展开计算即可得到答案.
【详解】(1)因为,,所以,
所以,.
(2).
【点睛】本题主要考查三角函数的恒等变换,同时考查同角三角函数关系,属于简单题.
15.(1)不符合要求
(2)按照修建,治疗区面积最大,最大值为(平方米)
【分析】(1)依题意求即可判断.
(2)设,用表示诊疗区域的面积即可.
(1)
当时,,
所以
因此诊断区不符合要求
(2)
设,则,
在中,,
在中,,,
所以
,其中,
所以,当且仅当即取等号
故按照修建,治疗区面积最大,最大值为(平方米).
16.(1)
(2)最大值和最小值分别为和
【分析】(1)代入已知点,由φ的范围可求得φ的值;
(2)由(1)得函数的解析式,再根据图象的平移和伸缩变换得出函数的解析式,由余弦函数的性质可求得其最值.
(1)
解:∵,且函数图像过点,
∴,即,解得,.
又,∴.
(2)
解: 由(1)知,将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像.
∵,∴,故.
∴在上的最大值和最小值分别为和.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
2.为了得到函数的图象,只需把余弦函数曲线上所有的点( )
A.向左平行移动个单位长度 B.向右平行移动个单位长度
C.向左平行移动个单位长度 D.向右平行移动个单位长度
3.达·芬奇的经典之作《蒙娜丽莎》举世闻名.如图,画中女子神秘的微笑,,数百年来让无数观赏者人迷.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行了粗略测绘,将画中女子的嘴唇近似看作一个圆弧,在嘴角处作圆弧的切线,两条切线交于点,测得如下数据:(其中).根据测量得到的结果推算:将《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角大约等于( )
A. B. C. D.
4.电流强度随时间变化的关系式是,则当时,电流强度为
A.5A B.2.5A C.2A D.-5A
5.已知某摩天轮的旋转半径为60米,最高点距地面135米,运行一周大约30分钟,某游客在最低点的位置坐上摩天轮,则第10分钟时他距地面大约为( )
A.95米 B.100米 C.105米 D.110米
6.函数的部分图象如图所示,则下列叙述正确的是
A.函数的图象可由的图象向左平移个单位得到
B.函数的图象关于直线对称
C.函数在区间上是单调递增的
D.函数图象的对称中心为
二、多选题
7.(多选题)如图所示的是一质点做简谐运动的图象,则下列结论正确的是( )
A.该质点的运动周期为0.7 s
B.该质点的振幅为5
C.该质点在0.1 s和0.5 s时运动速度为零
D.该质点的运动周期为0.8 s
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.如图,一个半径为的筒车按逆时针方向每分钟转1.5圈,筒车的轴心距离水面的高度为2米.设筒车上的某个盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计算时间,则与时间(单位:)之间的关系为(,,).则以下说法正确的有( )
A. B.
C. D.盛水筒出水后到达最高点的最小时间为
三、填空题
9.已知某海浴场的海浪高度是时间(其中,单位:时)的函数,记作,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,曲线可近似地看成是函数的图象,根据以上数据,函数的解析式为________.
10.在北京召开的第24届国际数学家大会的会标是根据中国古代数学家赵爽的“弦图”设计的.会标图案如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若直角三角形中较小锐角为,当小正方形的面积是大正方形面积的一半时,___________.
11.已知定义在R上的函数不是常数函数,写出一个同时具有下列三个性质的一个函数___________.
①;②;③.
12.筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时120秒,当时,盛水筒M位于点,经过t秒后运动到点,点P的纵坐标满足,则当筒车旋转100秒时,盛水筒M对应的点P的纵坐标为____________.
四、解答题
13.已知函数.
(1)求函数的最小正周期;
(2)求函数的最小值及相应的值.
14.已知,.
(1)求,的值;
(2)求的值.
15.2020年一场突如其来的疫情让亿万中华儿女的心再一次凝结在一起,为控制疫情,让广大发热患者得到及时有效的治疗,武汉市某社区决定临时修建一个医院.医院设计平面图如图所示:矩形中,米,米,图中区域为诊断区(、分别在和边上),、及区域为治疗区.受诊断区医疗设备的实际尺寸影响,要求的大小为.
(1)若按照米的方案修建医院,问诊断区是否符合要求?
(2)按照疫情现状,病人仍在不断增加,因此需要治疗区的面积尽可能的大,以便于增加床位,请给出具体的修建方案使得治疗区面积最大,并求出最大值.
16.已知函数,其图像过点.
(1)求φ的值;
(2)将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像,求函数在上的最大值和最小值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C【分析】由图中最小值求出,从而可得最大值.
【详解】由题干图易得ymin=k-3=2,则k=5.
∴ymax=k+3=8.
故选:C
【点睛】本题考查()的性质,的最大值为,最小值为.
2.C【解析】根据三角函数图象变换规律确定选项.
【详解】因为向左平行移动个单位长度得,
故选:C
【点睛】本题考查三角函数图象变换,考查基本分析判断能力,属基础题.
3.A【解析】由已知,设.可得.于是可得,进而得出结论.
【详解】解:依题意,设.
则.
,.
设《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角为.
则,
.
故选:A.
【点睛】本题考查了直角三角形的边角关系、三角函数的单调性、切线的性质,考查了推理能力与计算能力,属于中档题.
4.B【分析】由已知直接把代入,利用诱导公式及特殊角的三角函数值即可求出.
【详解】解:当时,.
故选:.
【点睛】本题考查三角函数的简单应用,属于基础题.
5.C【分析】设函数关系式为,根据题意求得各参数得解析式,然后计算可得.
【详解】设该游客在摩天轮上离地面高度(米)与时间t(分钟)的函数关系为,
由题意可知,,,所以,即.
又,得,故,
所以,
所以.
故选:C.
6.D【解析】根据题意求出解析式,利用正弦函数的对称性及单调性依次判断选项.
【详解】由图象可知A=2,f(0)=1,
∵f(0)=2sinφ=1,且,
∴,
∴f(x)=2sin(ωx),
∵f()=0且为单调递减时的零点,
∴,k∈Z,
∴,k∈Z,
由图象知,
∴ω,
又∵ω>0,
∴ω=2,
∴f(x)=2sin(2x),
∵函数f(x)的图象可由y=Asinωx的图象向左平移个单位得,
∴A错,
令2x,k∈Z,对称轴为x,则B错,
令2x,则x,则C错,
令2xkπ,k∈Z,则x=,则D对,
故选:D.
【点睛】本题考查三角函数图象及其性质,考查了正弦函数的对称性及单调性,属于中档题.
7.BCD【分析】由题图求得质点的振动周期可判定A错,D正确;由该质点的振幅,可判定B正确;由简谐运动的特点,可判定C正确.
【详解】由题图可知,质点的振动周期为2×(0.7-0.3)=0.8 s,所以A错,D正确;
该质点的振幅为5,所以B正确;
由简谐运动的特点知,质点处于平衡位置时的速度最大,即在0.3 s和0.7 s时运动速度最大,在0.1 s和0.5 s时运动速度为零,故C正确.
综上,BCD正确.
故选:BCD.
8.ABD【分析】由已知可得的值,得到函数解析式,取求得t的值,从而得解.
【详解】解:∵筒车按逆时针方向每分钟转1.5圈,,
则,故B正确;
振幅A为筒车的半径,即,故A正确;
由题意,t=0时,d=0,,即 ,
,∴,故C错误;
,
由d=6,得,
得
∴当k=0时,t取最小值为,故D正确.
故选:ABD.
9.【分析】由表中的数据可知,函数的最大值为1.5,最小值为0.5,从而可求出的值,再由表中的数据可得其最小正周期为12,从而可求出的值.
【详解】解:由题意得,,,
∴,.
又,∴.
从而.
故答案为:
【点睛】此题考查了三角函数模型的应用,掌握五点法是解题的关键,属于基础题.
10.【解析】设直角三角形直角边为,,令小正方形的面积为1,列方程组计算,,再根据锐角三角函数计算可得;.
【详解】解:设直角三角形中较长的直角边为,较短的直角边为,令小正方形的面积为1,则大正方形的面积为2,
则,解得或(舍去),
所以.
故答案为:.
11.(形式不唯一)【分析】由联想得到,可设,由周期性确定,猜想的值代入检验可确定.
【详解】解:由,
得,
联想到,
可推测.
由,
得,
则,
设,
则,所以满足题意.
故答案为:.(不唯一)
12.【分析】根据筒车按逆时针方向每旋转一周用时120秒,可求出,由时,求出和,从而可求出的关系式,进而可求出点P的纵坐标
【详解】因为筒车按逆时针方向每旋转一周用时120秒,
所以,得,
所以,
因为当时,盛水筒M位于点,
所以,
所以,
因为,
所以,得,
因为,所以,
所以,
所以,
所以当筒车旋转100秒时,盛水筒M对应的点P的纵坐标为,
故答案为:
13.(1)(2)的最小值为,此时.【分析】通过倍角公式,把化成标准形式,研究函数的相关性质(周期性,单调性,奇偶性,对称性,最值及最值相对于的变量),从而本题能顺利完成
【详解】(1)因为.
所以函数的最小正周期为.
(2)当时,,
此时,,,
所以的最小值为,此时.
【点睛】该类型考题关键是将化成性质,只有这样,我们才能很好的去研究他的性质.
14.(1),;(2)【分析】(1)首先利用同角三角函数关系求出,从而得到,再利用正弦二倍角公式计算即可.
(2)利用正弦两角差公式展开计算即可得到答案.
【详解】(1)因为,,所以,
所以,.
(2).
【点睛】本题主要考查三角函数的恒等变换,同时考查同角三角函数关系,属于简单题.
15.(1)不符合要求
(2)按照修建,治疗区面积最大,最大值为(平方米)
【分析】(1)依题意求即可判断.
(2)设,用表示诊疗区域的面积即可.
(1)
当时,,
所以
因此诊断区不符合要求
(2)
设,则,
在中,,
在中,,,
所以
,其中,
所以,当且仅当即取等号
故按照修建,治疗区面积最大,最大值为(平方米).
16.(1)
(2)最大值和最小值分别为和
【分析】(1)代入已知点,由φ的范围可求得φ的值;
(2)由(1)得函数的解析式,再根据图象的平移和伸缩变换得出函数的解析式,由余弦函数的性质可求得其最值.
(1)
解:∵,且函数图像过点,
∴,即,解得,.
又,∴.
(2)
解: 由(1)知,将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像.
∵,∴,故.
∴在上的最大值和最小值分别为和.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
