直线方程(第一课时)[上学期]
文档属性
| 名称 | 直线方程(第一课时)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 313.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-10 19:00:00 | ||
图片预览






文档简介
课件18张PPT。直线方程进入Ⅰ.复习:1.两点间的距离公式已知两点P1(x1,y1),P2(x2,y2),那么两点P1,P2之间的
距离公式为:2.线段的中点公式两点P1(x1,y1),P2(x2,y2)之间线段中点P的坐标为:练习:1.已知两点A(3,-1),B(2,1),求点A关于点B的对称点C,
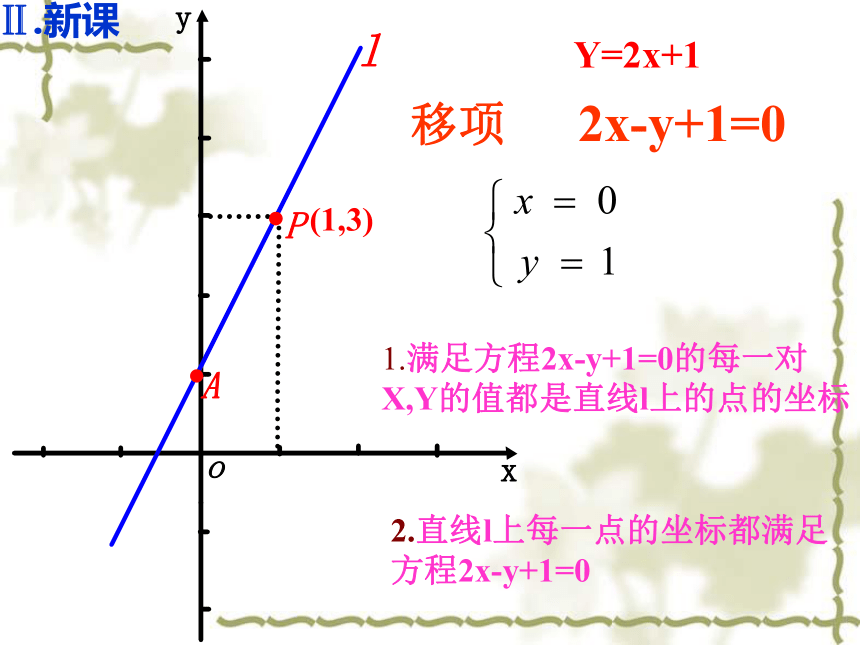
并求︱AC︳。解:由题意得B为线段AC中点,设C(x,y),则有解得:x=1 , y=3∴C点坐标为(1,3)Y=2x+11.满足方程2x-y+1=0的每一对
X,Y的值都是直线l上的点的坐标2.直线l上每一点的坐标都满足
方程2x-y+1=0Ⅱ.新课(1,3)移项 2x-y+1=0一般地,若方程kx-y+b=0与直线具有下列对应关系:(1)以方程kx-y+b=0的每一组解x,y为坐标的
点(x,y)都在直线l上(2)在直线l上的任一点的坐标(x,y)都是
方程kx-y+b=0的解 此时把方程kx-y+b=0称作直线l的方程,直线l
称作这个方程kx-y+b=0的图象直线方程一. 概念:二﹑直线的倾斜角和斜率:直线l 的向上方向与x轴的正方向所成的最小正角00≤?<18001.倾斜角:2.斜率: 当直线l 的倾斜角?≠900时,倾斜角?的
正切值,即 tan ?k=tan ? 练习1:已知直线的倾斜角,讨论这条直线的斜率的值:K=0K>0不存在k<0记为 k即例1. 如图,等边三角形OAB,O为坐标原点,
顶点B在y轴的正半轴上,分别求OA﹑AB﹑OB
所在直线的倾斜角和斜率。解:∵∠BOA=600 , ∴?=300∴直线OA的倾斜角是300 ,它的斜率K1=tan300=P∵∠ABO=600 ∴直线AB的倾斜角?=600+900 =1500它的斜率k2=tan1500=∵直线OB和y轴重合, ∴它的倾斜角为900,斜率不存在练习:已知直线的倾斜角如下,求各直线的斜率:loxy?P1 (x1,y1) P2 (x2,y2)Q (x2, y1)M1M2P1(x1,y1) ﹑P2(x2,y2)?=?QP1P2∴tan ?=tan ?QP1P2==? 经过点P1(x1,y1) ﹑P2(x2,y2)两点的
直线斜率公式:例2求经过P1(-2,0), P2(-5,3)两点的直线的
斜率和倾斜角解:由斜率公式得K=3﹣0﹣5﹣(﹣2)=﹣1练习2: 已知P,Q是直线l上的两点,求直线l的
斜率和倾斜角(1)P(3,3), Q(-3,-3), ?=?=(3)P(4,4), Q(-4,4)(4)P(1,1),Q(1,-1), ?=0斜率不存在?=900(2)P(-2,0), Q(-5,3)?=例3已知三角形的三个顶点A(1,2) ﹑B(5,3) ﹑C(4,-2)
求:(1)三角形AB边所在的直线的斜率和倾斜角
(2)AB边上的中点所在的直线的斜率和倾斜角解(1)设AB边所在直线的倾斜角为?,
则(2)D为AB中点,设CD所在直线斜率为kCD倾斜角为?,则例3证明三点A(2,3),B(1,﹣3),C(3,9)
在同一条直线上证:KAB=kAC =∵直线AB和AC的斜率相等,而它们经过同一点A
∴A,B,C三点在同一条直线上练习3;判断下列各题中所给三点是否在同一直线上:(1)A(2,3), B(1,-3), C(3,9)(2)A(2,1), B(3,-2), C(-4,-1)(3)A(a-b,c-a), B(0,0), C(b-a,a-c)kAB=kBC=6kAB=-3kAB=kBC=kBC=-1/7小结:(1)直线方程的概念
(2)直线的倾斜角?
(3)直线的斜率k=tan ?=作业:课本P247
习题9-2 A组 1,2回答下列问题:1.直线的倾斜角有没有限制?2.平行于x轴的直线的倾斜角是什么?
平行于y轴的呢?3.所有的直线都有倾斜角吗?4.所有的直线都有斜率吗?为什么? 00≤?<180000900是不是当?=900时,斜率不存在练习 如图,直线l1的倾斜角?1=300,直线l2⊥l1,
求l1﹑l2的斜率解:l1的斜率k1=tan300=∵l2的倾斜角?2=900+300=1200∴l2的斜率k2=tan1200=﹣tan600=
距离公式为:2.线段的中点公式两点P1(x1,y1),P2(x2,y2)之间线段中点P的坐标为:练习:1.已知两点A(3,-1),B(2,1),求点A关于点B的对称点C,
并求︱AC︳。解:由题意得B为线段AC中点,设C(x,y),则有解得:x=1 , y=3∴C点坐标为(1,3)Y=2x+11.满足方程2x-y+1=0的每一对
X,Y的值都是直线l上的点的坐标2.直线l上每一点的坐标都满足
方程2x-y+1=0Ⅱ.新课(1,3)移项 2x-y+1=0一般地,若方程kx-y+b=0与直线具有下列对应关系:(1)以方程kx-y+b=0的每一组解x,y为坐标的
点(x,y)都在直线l上(2)在直线l上的任一点的坐标(x,y)都是
方程kx-y+b=0的解 此时把方程kx-y+b=0称作直线l的方程,直线l
称作这个方程kx-y+b=0的图象直线方程一. 概念:二﹑直线的倾斜角和斜率:直线l 的向上方向与x轴的正方向所成的最小正角00≤?<18001.倾斜角:2.斜率: 当直线l 的倾斜角?≠900时,倾斜角?的
正切值,即 tan ?k=tan ? 练习1:已知直线的倾斜角,讨论这条直线的斜率的值:K=0K>0不存在k<0记为 k即例1. 如图,等边三角形OAB,O为坐标原点,
顶点B在y轴的正半轴上,分别求OA﹑AB﹑OB
所在直线的倾斜角和斜率。解:∵∠BOA=600 , ∴?=300∴直线OA的倾斜角是300 ,它的斜率K1=tan300=P∵∠ABO=600 ∴直线AB的倾斜角?=600+900 =1500它的斜率k2=tan1500=∵直线OB和y轴重合, ∴它的倾斜角为900,斜率不存在练习:已知直线的倾斜角如下,求各直线的斜率:loxy?P1 (x1,y1) P2 (x2,y2)Q (x2, y1)M1M2P1(x1,y1) ﹑P2(x2,y2)?=?QP1P2∴tan ?=tan ?QP1P2==? 经过点P1(x1,y1) ﹑P2(x2,y2)两点的
直线斜率公式:例2求经过P1(-2,0), P2(-5,3)两点的直线的
斜率和倾斜角解:由斜率公式得K=3﹣0﹣5﹣(﹣2)=﹣1练习2: 已知P,Q是直线l上的两点,求直线l的
斜率和倾斜角(1)P(3,3), Q(-3,-3), ?=?=(3)P(4,4), Q(-4,4)(4)P(1,1),Q(1,-1), ?=0斜率不存在?=900(2)P(-2,0), Q(-5,3)?=例3已知三角形的三个顶点A(1,2) ﹑B(5,3) ﹑C(4,-2)
求:(1)三角形AB边所在的直线的斜率和倾斜角
(2)AB边上的中点所在的直线的斜率和倾斜角解(1)设AB边所在直线的倾斜角为?,
则(2)D为AB中点,设CD所在直线斜率为kCD倾斜角为?,则例3证明三点A(2,3),B(1,﹣3),C(3,9)
在同一条直线上证:KAB=kAC =∵直线AB和AC的斜率相等,而它们经过同一点A
∴A,B,C三点在同一条直线上练习3;判断下列各题中所给三点是否在同一直线上:(1)A(2,3), B(1,-3), C(3,9)(2)A(2,1), B(3,-2), C(-4,-1)(3)A(a-b,c-a), B(0,0), C(b-a,a-c)kAB=kBC=6kAB=-3kAB=kBC=kBC=-1/7小结:(1)直线方程的概念
(2)直线的倾斜角?
(3)直线的斜率k=tan ?=作业:课本P247
习题9-2 A组 1,2回答下列问题:1.直线的倾斜角有没有限制?2.平行于x轴的直线的倾斜角是什么?
平行于y轴的呢?3.所有的直线都有倾斜角吗?4.所有的直线都有斜率吗?为什么? 00≤?<180000900是不是当?=900时,斜率不存在练习 如图,直线l1的倾斜角?1=300,直线l2⊥l1,
求l1﹑l2的斜率解:l1的斜率k1=tan300=∵l2的倾斜角?2=900+300=1200∴l2的斜率k2=tan1200=﹣tan600=
