直线方程与线性规划[上学期]
图片预览








文档简介
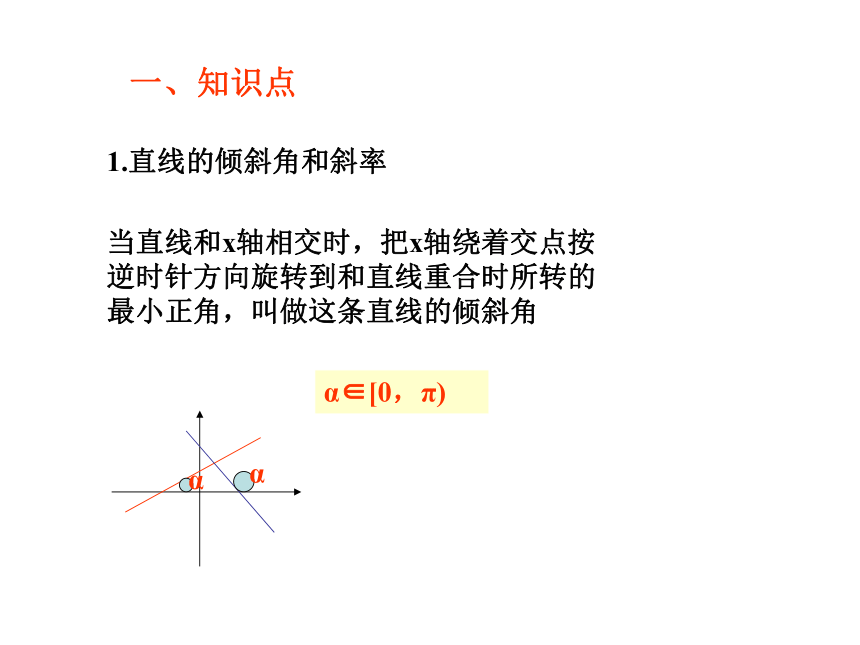
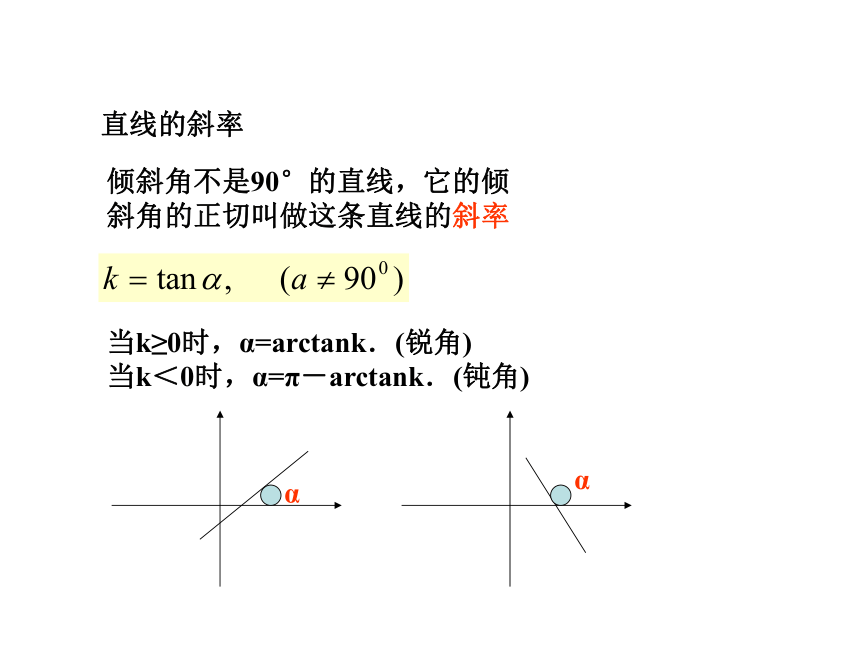
课件43张PPT。高中数学第七章直线与圆方程复习直线方程与线性规划一、知识点1.直线的倾斜角和斜率 当直线和x轴相交时,把x轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角,叫做这条直线的倾斜角 α α α∈[0,π) 倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率直线的斜率当k≥0时,α=arctank.(锐角)
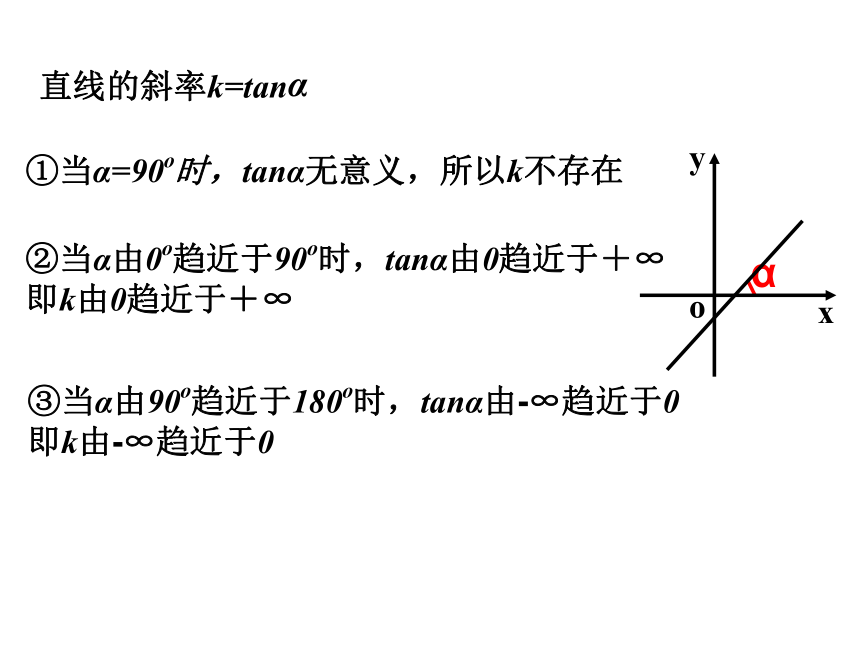
当k<0时,α=π-arctank.(钝角)ααα直线的斜率k=tanα①当α=90o时,tanα无意义,所以k不存在②当α由0o趋近于90o时,tanα由0趋近于+∞
即k由0趋近于+∞③当α由90o趋近于180o时,tanα由-∞趋近于0
即k由-∞趋近于0 斜率公式 经过两点P1(x1,y1)、 P2(x2,y2)的直线的斜率为P1(x1,y1)P2(x2,y2)向量 P1P2称为直线的方向向量向量 P1P2的坐标为(x2-x1, y2-y1)每条直线的倾斜角是唯一的,但不是每条直线都存在斜率.①直线方程的点斜式:
直线的斜率为k,且经过点P( x1,y1 ),则直线的方程是:说明:
1、这个方程是由直线上一点和斜率确定的;
2、当直线的倾斜角为0°时,直线方程为y=y1;
3、当直线倾斜角90 °时,直线没有斜率,它的方程不能用点斜式表示,这时直线方程为x=x1。
2.直线方程的形式P直线的斜率为k,与y轴的交点是(0,b),则直线 l 的方程是:
说明:
1、上述方程是由直线的斜率和它在y轴上的截距确定的,叫做直线方程的斜截式。
2、我们称b为直线在y轴上截距。
3、截距b可以大于0,也可以等于或小于0。②直线方程的斜截式③直线方程的两点式经过点P1( x1,y1 )、P2( x2,y2 )的直线的方程是:说明:
1、这个方程是由直线上两点确定的;
2、当直线的倾斜角为0°时(y=y1) ,或当直线倾斜角90 °为时(x=x1) ,它的方程不能用两点式求出。
3、经过点P1(x1,y1)、P2(x2,y2)的所有直线的方程可以写成
(y-y1)(x2-x1)=(y2-y1)(x-x1)直线l与x轴的交点为P1(a,0),与y轴的交点为P2(0,b),其中a≠0,b≠0,则直线 l 的方程是:说明:1这一直线方程由直线在x轴和y轴上截距确定,所以叫做直线方程的截距式;
2截距式适用于横、纵截距都存在且不为0的直线。④直线方程的截距式⑤直线方程的一般式: 说明:在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的二元一次方程。 在平面直角坐标系中,任何关于x,y的二元一次方程都表示一条直线。例1:直线 过点 (-1,3),倾斜角的正弦是 求直线 的方程.解:因为倾斜角 的范围是:
又由题意:
所以: 直线过点 (-1,3),由直线的点斜式方程得到:
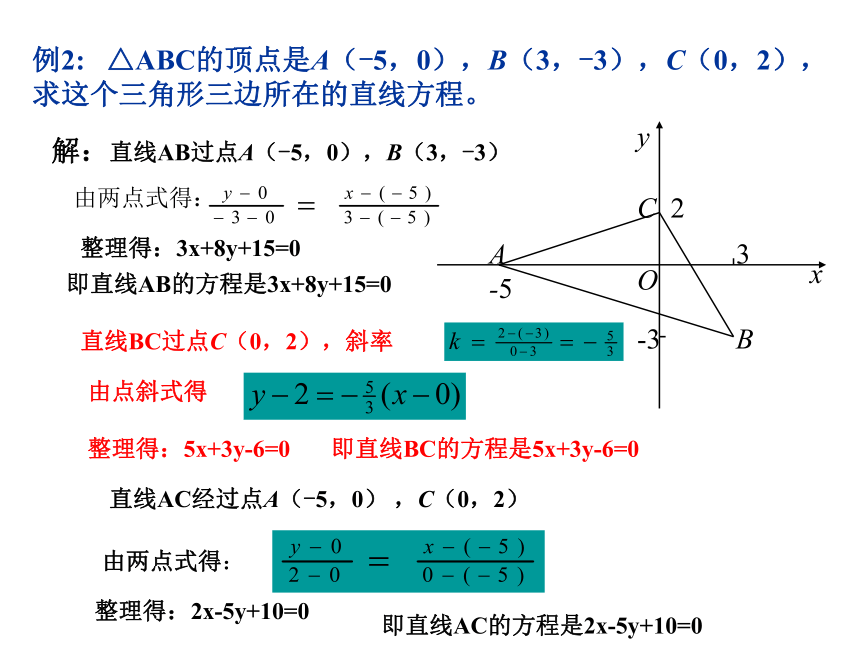
即:4x-3y+13=0 或 4x+3y-5=0二、重要题型剖析例2: △ABC的顶点是A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在的直线方程。解:直线AB过点A(-5,0),B(3,-3)由两点式得:整理得:3x+8y+15=0即直线AB的方程是3x+8y+15=0直线AC经过点A(-5,0) ,C(0,2)由两点式得:整理得:2x-5y+10=0即直线AC的方程是2x-5y+10=0直线BC过点C(0,2),斜率由点斜式得整理得:5x+3y-6=0即直线BC的方程是5x+3y-6=0例3:直线 l过点P(3,2)且与x、y轴的正半轴分别相交于A、B两点,△OAB的面积是12,求直线l 的方程方法1,题中的△OAB的面积与截距有关,可利用直线方程的截距式解:设直线的方程是所以,A(a,0),B(0,b)所以,所求直线的方程是即:2x+3y-12=0方法2:注意到直线过点P(3,2),只缺斜率,故利用直线方程的点斜式。解:设直线的方程是y-2=k(x-3)(k<0)令y=0得直线在x轴的截距令x=0得直线在y轴的截距b=2-3k所以,所以直线的方程是即2x+3y-12=03.两条直线的位置关系 (1)平行: 斜截式方程: y=k1x+b1, y=k2x+b2
k1=k2且b1≠b2 (2)重合: 斜截式方程: y=k1x+b1, y=k2x+b2
k1=k2且b1=b2 (3)相交: 当l1,l2是斜截式方程时,k1≠k2l1到l2的角 两条直线l1和l2相交构成四个角,它们是两对对顶角.为了区别这些角,我们把直线l1按逆时针方向旋转到与l2重合时所转的角,叫做l1到l2的角,在图中,直线l1到l2的角是θ1,l2到l1的角是θ2 (θ1>0,θ2>0,且θ1+θ2=π) l1l2θ1θ2斜率为 k1、k2 的两条直线 l1 到 l2 的角θ l1 :y=k1x+b1,l2:y=k2x+b2. θ=α2-α1 或 π+(α2-α1).tanθ=tan(α2-α1)或 tan[π+(α2-α1)] ∴tanθ=tan(α2-α1)因为l2到l1的角等于π-θ,所以当直线l1与l2相交但不垂直时,在θ和π-θ中有且仅有一个角是锐角,我们把其中的锐角叫做两条直线的夹角.记夹角为α。 两条直线的夹角当 1+k1k1=0时,两直线垂直两直线垂直的充要条件:k1k2= -1或A1A2+B1B2=0两条直线的交点点P(x0,y0)与直线 l:Ax+By+C=0的位置关系 点P(x0,y0)与直线 l 的距离两条平行直线 l1∶Ax+By+C1=0,
l2∶Ax+By+C2=0
间的距离4.直线系方程 具有某一共同属性的一类直线的集合称为直线系,它的方程的特点是除含坐标变量x,y以外,还含有特定的系数(也称参变量).(1)共点直线系方程 经过两直线 l1∶A1x+B1y+C1=0,
l2∶A2x+B2y+C2=0
的交点的直线系方程为:
A1x+B1y+C1+λ(A2x+B2y+C2)=0,其中λ是待定的系数.(2). 平行直线系方程: 直线 y=kx+b中当斜率k一定而b变动时,表示平行直线系方程. y=kx+b+λ, (λ≠0)
与直线Ax+By+C=0平行的直线系方程是
Ax+By+λ=0(λ≠C),λ是参变量.(3). 垂直直线系方程:求直线方程的问题中,有一个已知条件,另一个条件待定时,可选用直线系方程来求解
(4)直线过定点
如直线(3m+4)x+(5-2m)y+7m-6=0,不论m取
何值恒过定点(-1,2) 5.简单的线性规划 (1)二元一次不等式:Ax+By+C>0(或<0)
表示直线Ax+By+C=0某一侧所有点组成的平面区域.Ax+By+C=0Ax+By+C<0Ax+By+C>0包括边界时,直线画成实线;
不包括边界时,画成虚线。Ax+By+C≤0Ax+By+C≥0Ax+By+C=0特殊地,当C≠0时,常把原点作为此特殊点. 怎么判断在直线的那一侧直线Ax+By+C=0 同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同。所以只需在此直线的某一侧取一个特殊点
(x0,y0),从Ax0+By0+C的正负即可判断
Ax+By+C>0表示直线哪一侧的平面区域.2x-y+3>02x+y+3>0设 z = 2x + y 且变量 x、y 满足下列条件
求z 的最大值和最小值由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数(2).简单的线性规划有关概念设 z = 2x + y 且变量 x、y 满足下列条件
求z 的最大值和最小值(2).简单的线性规划有关概念求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解(3)解线性规划问题的步骤: (2)移:在线性目标函数所表示的一组平行
线中,利用平移的方法找出与可行域有公共
点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案(1)画:画出线性约束条件所表示的可行域;例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.解法一:设B(x1,y1),由题意可得:所以BC边所在的直线的方程为:二、重要题型剖析例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.解法二:设B(x1,y1)由题意可得:由x-4y+10=0为∠B的平分线知,
A(3,-1)关于直线x-4y+10=0的对称点A’(1,7)
在BC边所在的直线上,所以BC边所在的直线的方程为:例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.点评:本题在处理角平分线时,
(1)利用直线BC到BT的角等于BT到AB的角
进而利用到角公式求得直线BC的斜率;
(2)由直线BT是∠B的角平分线,可得到A点关于直线
BT的对称点A′在直线BC上,则直线BC的方程即
为直线BA′的方程.例5:过点 P(3,0)作直线l,使它被两相交直线2x-y-2=0 和x+y+3=0 所截得的线段AB 恰好被 P点平分,求直线l的方程. 解:设 A点坐标(x1 ,y1 )
∵线段AB 的中点为P(3,0)∴ 由中点公式,可设 B点坐标为(6-x1,-y1)∵A、B两点分别在直线 2x-y-2=0 和x+y+3=0 上
∴???解得???
由两点式可得直线 的方程为:8x-y-24=0 ??? ????????????
x+y+3=02x-y-2=0PAB 例6:直线l 过点 M(2,1),且分别交x 轴、 y轴的正半轴于点 A、B .点O是坐标原点,(1)求当△ABO 面积最小时直线 l方程;(2)当|MA||MB| 最小时,求直线l 的方程. (1)如图,设 |OA|=a ,|OB|=b , △ABO 的面积为S则????
并且直线 的截距式方程是 由直线通过点(2,1),得 当且仅当 ,即b=2 时,面积 S取最小值4, 这时 ,直线的方程是:
即: x+2y-4=0演示(2)设∠BAO=θ ,则 当θ=450时,|MA||MB|有最小值4此时k=1 ,直线 的方程为x+y-3=0 . ACBX=1X-4y+3=03x+5y-25=02x+y=0例8 某工厂生产甲、乙两种产品.已知生产甲种产品1 t,需耗A种矿石10 t、B种矿石5 t、煤4 t;生产乙种产品需耗A种矿石4 t、B种矿石4 t、煤9 t.每1 t甲种产品的利润是600元,每1 t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过360 t、B种矿石不超过200 t、煤不超过300 t,甲、乙两种产品应各生产多少(精确到0.1 t),能使利润总额达到最大? 解:设生产甲、乙两种产品分别为x t、y t,利润总额为z元 约束条件 目标函数为:z=600x+1000y. MM(12.4,34.4)M(12.4,34.4)1.设θ∈R,则直线xsinθ-√3y+1=0的倾斜角的取值范围
为____________________________________2.已知点P(1,2),直线l:2x+y-1=0,则
过点P且与直线l平行的直线方程为__________;
过点P且与直线l垂直的直线方程为___________;
过点P且直线l夹角为45°的直线方程为 ;
点P到直线L的距离为 ;
直线L与直线4x+2y-3=0的距离为_________.3.若直线l1:mx+2y+6=0和直线l2:x+(m-1)y+m2-1=0平行但
不重合,则m的值是______.[0°,30°]∪[150°,180°). 2x+y-4=0x-2y+3=03x-y-1=0或
x+3y-7=0-1a=1或-3练习5.直线l 在x,y轴上截距的倒数和为常数1/m,则直线过定点___________6.若直线l1:y=kx+k+2与l2:y= -2x+4的交点在第一象限,则k的取值范围是______________-2/3<k<27.平面内满足不等式组 的所
有点中,使目标函数 z=5x+4y取得最大值的点的坐标是________(m,m)8.已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x-3y+16=0,CA:2x+y-2=0求:(1)AC边上的高所在的直线方程;
(2)∠ABC的平分线所在的直线方程;
(3)AB与AC边上的中点连线所在的直线方程.
当k<0时,α=π-arctank.(钝角)ααα直线的斜率k=tanα①当α=90o时,tanα无意义,所以k不存在②当α由0o趋近于90o时,tanα由0趋近于+∞
即k由0趋近于+∞③当α由90o趋近于180o时,tanα由-∞趋近于0
即k由-∞趋近于0 斜率公式 经过两点P1(x1,y1)、 P2(x2,y2)的直线的斜率为P1(x1,y1)P2(x2,y2)向量 P1P2称为直线的方向向量向量 P1P2的坐标为(x2-x1, y2-y1)每条直线的倾斜角是唯一的,但不是每条直线都存在斜率.①直线方程的点斜式:
直线的斜率为k,且经过点P( x1,y1 ),则直线的方程是:说明:
1、这个方程是由直线上一点和斜率确定的;
2、当直线的倾斜角为0°时,直线方程为y=y1;
3、当直线倾斜角90 °时,直线没有斜率,它的方程不能用点斜式表示,这时直线方程为x=x1。
2.直线方程的形式P直线的斜率为k,与y轴的交点是(0,b),则直线 l 的方程是:
说明:
1、上述方程是由直线的斜率和它在y轴上的截距确定的,叫做直线方程的斜截式。
2、我们称b为直线在y轴上截距。
3、截距b可以大于0,也可以等于或小于0。②直线方程的斜截式③直线方程的两点式经过点P1( x1,y1 )、P2( x2,y2 )的直线的方程是:说明:
1、这个方程是由直线上两点确定的;
2、当直线的倾斜角为0°时(y=y1) ,或当直线倾斜角90 °为时(x=x1) ,它的方程不能用两点式求出。
3、经过点P1(x1,y1)、P2(x2,y2)的所有直线的方程可以写成
(y-y1)(x2-x1)=(y2-y1)(x-x1)直线l与x轴的交点为P1(a,0),与y轴的交点为P2(0,b),其中a≠0,b≠0,则直线 l 的方程是:说明:1这一直线方程由直线在x轴和y轴上截距确定,所以叫做直线方程的截距式;
2截距式适用于横、纵截距都存在且不为0的直线。④直线方程的截距式⑤直线方程的一般式: 说明:在平面直角坐标系中,对于任何一条直线,都有一个表示这条直线的关于x,y的二元一次方程。 在平面直角坐标系中,任何关于x,y的二元一次方程都表示一条直线。例1:直线 过点 (-1,3),倾斜角的正弦是 求直线 的方程.解:因为倾斜角 的范围是:
又由题意:
所以: 直线过点 (-1,3),由直线的点斜式方程得到:
即:4x-3y+13=0 或 4x+3y-5=0二、重要题型剖析例2: △ABC的顶点是A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在的直线方程。解:直线AB过点A(-5,0),B(3,-3)由两点式得:整理得:3x+8y+15=0即直线AB的方程是3x+8y+15=0直线AC经过点A(-5,0) ,C(0,2)由两点式得:整理得:2x-5y+10=0即直线AC的方程是2x-5y+10=0直线BC过点C(0,2),斜率由点斜式得整理得:5x+3y-6=0即直线BC的方程是5x+3y-6=0例3:直线 l过点P(3,2)且与x、y轴的正半轴分别相交于A、B两点,△OAB的面积是12,求直线l 的方程方法1,题中的△OAB的面积与截距有关,可利用直线方程的截距式解:设直线的方程是所以,A(a,0),B(0,b)所以,所求直线的方程是即:2x+3y-12=0方法2:注意到直线过点P(3,2),只缺斜率,故利用直线方程的点斜式。解:设直线的方程是y-2=k(x-3)(k<0)令y=0得直线在x轴的截距令x=0得直线在y轴的截距b=2-3k所以,所以直线的方程是即2x+3y-12=03.两条直线的位置关系 (1)平行: 斜截式方程: y=k1x+b1, y=k2x+b2
k1=k2且b1≠b2 (2)重合: 斜截式方程: y=k1x+b1, y=k2x+b2
k1=k2且b1=b2 (3)相交: 当l1,l2是斜截式方程时,k1≠k2l1到l2的角 两条直线l1和l2相交构成四个角,它们是两对对顶角.为了区别这些角,我们把直线l1按逆时针方向旋转到与l2重合时所转的角,叫做l1到l2的角,在图中,直线l1到l2的角是θ1,l2到l1的角是θ2 (θ1>0,θ2>0,且θ1+θ2=π) l1l2θ1θ2斜率为 k1、k2 的两条直线 l1 到 l2 的角θ l1 :y=k1x+b1,l2:y=k2x+b2. θ=α2-α1 或 π+(α2-α1).tanθ=tan(α2-α1)或 tan[π+(α2-α1)] ∴tanθ=tan(α2-α1)因为l2到l1的角等于π-θ,所以当直线l1与l2相交但不垂直时,在θ和π-θ中有且仅有一个角是锐角,我们把其中的锐角叫做两条直线的夹角.记夹角为α。 两条直线的夹角当 1+k1k1=0时,两直线垂直两直线垂直的充要条件:k1k2= -1或A1A2+B1B2=0两条直线的交点点P(x0,y0)与直线 l:Ax+By+C=0的位置关系 点P(x0,y0)与直线 l 的距离两条平行直线 l1∶Ax+By+C1=0,
l2∶Ax+By+C2=0
间的距离4.直线系方程 具有某一共同属性的一类直线的集合称为直线系,它的方程的特点是除含坐标变量x,y以外,还含有特定的系数(也称参变量).(1)共点直线系方程 经过两直线 l1∶A1x+B1y+C1=0,
l2∶A2x+B2y+C2=0
的交点的直线系方程为:
A1x+B1y+C1+λ(A2x+B2y+C2)=0,其中λ是待定的系数.(2). 平行直线系方程: 直线 y=kx+b中当斜率k一定而b变动时,表示平行直线系方程. y=kx+b+λ, (λ≠0)
与直线Ax+By+C=0平行的直线系方程是
Ax+By+λ=0(λ≠C),λ是参变量.(3). 垂直直线系方程:求直线方程的问题中,有一个已知条件,另一个条件待定时,可选用直线系方程来求解
(4)直线过定点
如直线(3m+4)x+(5-2m)y+7m-6=0,不论m取
何值恒过定点(-1,2) 5.简单的线性规划 (1)二元一次不等式:Ax+By+C>0(或<0)
表示直线Ax+By+C=0某一侧所有点组成的平面区域.Ax+By+C=0Ax+By+C<0Ax+By+C>0包括边界时,直线画成实线;
不包括边界时,画成虚线。Ax+By+C≤0Ax+By+C≥0Ax+By+C=0特殊地,当C≠0时,常把原点作为此特殊点. 怎么判断在直线的那一侧直线Ax+By+C=0 同一侧的所有点(x,y),把它的坐标(x,y)代入Ax+By+C,所得到实数的符号都相同。所以只需在此直线的某一侧取一个特殊点
(x0,y0),从Ax0+By0+C的正负即可判断
Ax+By+C>0表示直线哪一侧的平面区域.2x-y+3>02x+y+3>0设 z = 2x + y 且变量 x、y 满足下列条件
求z 的最大值和最小值由x,y 的不等式(或方程)组成的不等式组称为x,y 的约束条件。关于x,y 的一次不等式或方程组成的不等式组称为x,y 的线性约束条件。欲达到最大值或最小值所涉及的变量x,y 的解析式称为目标函数。关于x,y 的一次目标函数称为线性目标函数(2).简单的线性规划有关概念设 z = 2x + y 且变量 x、y 满足下列条件
求z 的最大值和最小值(2).简单的线性规划有关概念求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解(x,y)称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解(3)解线性规划问题的步骤: (2)移:在线性目标函数所表示的一组平行
线中,利用平移的方法找出与可行域有公共
点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案(1)画:画出线性约束条件所表示的可行域;例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.解法一:设B(x1,y1),由题意可得:所以BC边所在的直线的方程为:二、重要题型剖析例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.解法二:设B(x1,y1)由题意可得:由x-4y+10=0为∠B的平分线知,
A(3,-1)关于直线x-4y+10=0的对称点A’(1,7)
在BC边所在的直线上,所以BC边所在的直线的方程为:例4、已知△ABC的顶点A(3,-1),AB边上的中线所在
直线方程为6x+10y-59=0,∠B的平分线所在直线
的方程为:x-4y+10=0,求BC边所在的直线的方程.点评:本题在处理角平分线时,
(1)利用直线BC到BT的角等于BT到AB的角
进而利用到角公式求得直线BC的斜率;
(2)由直线BT是∠B的角平分线,可得到A点关于直线
BT的对称点A′在直线BC上,则直线BC的方程即
为直线BA′的方程.例5:过点 P(3,0)作直线l,使它被两相交直线2x-y-2=0 和x+y+3=0 所截得的线段AB 恰好被 P点平分,求直线l的方程. 解:设 A点坐标(x1 ,y1 )
∵线段AB 的中点为P(3,0)∴ 由中点公式,可设 B点坐标为(6-x1,-y1)∵A、B两点分别在直线 2x-y-2=0 和x+y+3=0 上
∴???解得???
由两点式可得直线 的方程为:8x-y-24=0 ??? ????????????
x+y+3=02x-y-2=0PAB 例6:直线l 过点 M(2,1),且分别交x 轴、 y轴的正半轴于点 A、B .点O是坐标原点,(1)求当△ABO 面积最小时直线 l方程;(2)当|MA||MB| 最小时,求直线l 的方程. (1)如图,设 |OA|=a ,|OB|=b , △ABO 的面积为S则????
并且直线 的截距式方程是 由直线通过点(2,1),得 当且仅当 ,即b=2 时,面积 S取最小值4, 这时 ,直线的方程是:
即: x+2y-4=0演示(2)设∠BAO=θ ,则 当θ=450时,|MA||MB|有最小值4此时k=1 ,直线 的方程为x+y-3=0 . ACBX=1X-4y+3=03x+5y-25=02x+y=0例8 某工厂生产甲、乙两种产品.已知生产甲种产品1 t,需耗A种矿石10 t、B种矿石5 t、煤4 t;生产乙种产品需耗A种矿石4 t、B种矿石4 t、煤9 t.每1 t甲种产品的利润是600元,每1 t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过360 t、B种矿石不超过200 t、煤不超过300 t,甲、乙两种产品应各生产多少(精确到0.1 t),能使利润总额达到最大? 解:设生产甲、乙两种产品分别为x t、y t,利润总额为z元 约束条件 目标函数为:z=600x+1000y. MM(12.4,34.4)M(12.4,34.4)1.设θ∈R,则直线xsinθ-√3y+1=0的倾斜角的取值范围
为____________________________________2.已知点P(1,2),直线l:2x+y-1=0,则
过点P且与直线l平行的直线方程为__________;
过点P且与直线l垂直的直线方程为___________;
过点P且直线l夹角为45°的直线方程为 ;
点P到直线L的距离为 ;
直线L与直线4x+2y-3=0的距离为_________.3.若直线l1:mx+2y+6=0和直线l2:x+(m-1)y+m2-1=0平行但
不重合,则m的值是______.[0°,30°]∪[150°,180°). 2x+y-4=0x-2y+3=03x-y-1=0或
x+3y-7=0-1a=1或-3练习5.直线l 在x,y轴上截距的倒数和为常数1/m,则直线过定点___________6.若直线l1:y=kx+k+2与l2:y= -2x+4的交点在第一象限,则k的取值范围是______________-2/3<k<27.平面内满足不等式组 的所
有点中,使目标函数 z=5x+4y取得最大值的点的坐标是________(m,m)8.已知△ABC三边所在直线方程为AB:3x+4y+12=0,BC:4x-3y+16=0,CA:2x+y-2=0求:(1)AC边上的高所在的直线方程;
(2)∠ABC的平分线所在的直线方程;
(3)AB与AC边上的中点连线所在的直线方程.
