直线与圆的位置关系[上学期]

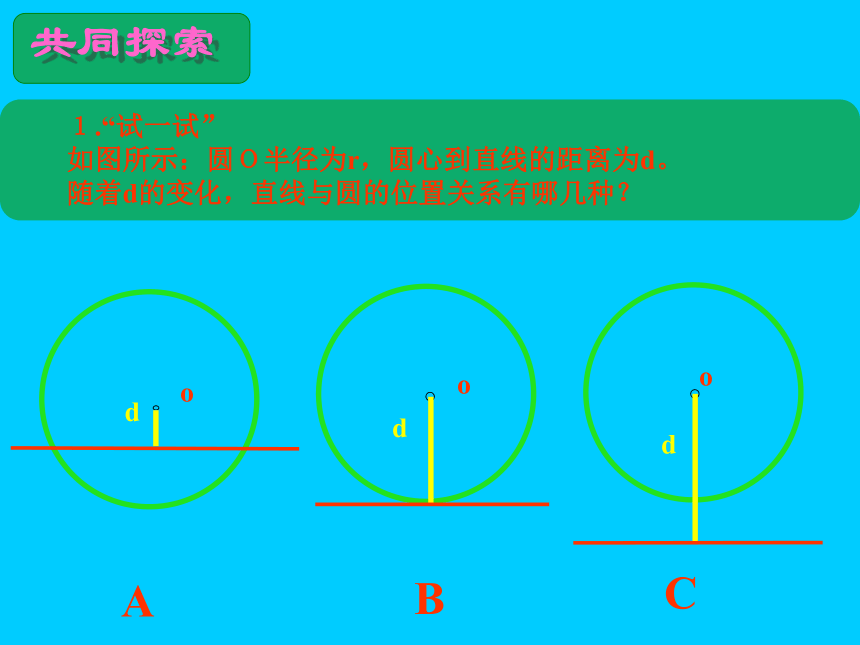
课件20张PPT。例　　题共同探索随堂练习课堂小结作　　业鄱阳二中　　　姜德林直线与圆的位置关系１.“试一试”
如图所示：圆Ｏ半径为r，圆心到直线的距离为d。
随着d的变化，直线与圆的位置关系有哪几种？o共同探索共同探索odCooddBA１.“试一试”
如图所示：圆Ｏ半径为r，圆心到直线的距离为d。
随着d的变化，直线与圆的位置关系有哪几种？直线与圆的位置关系有:
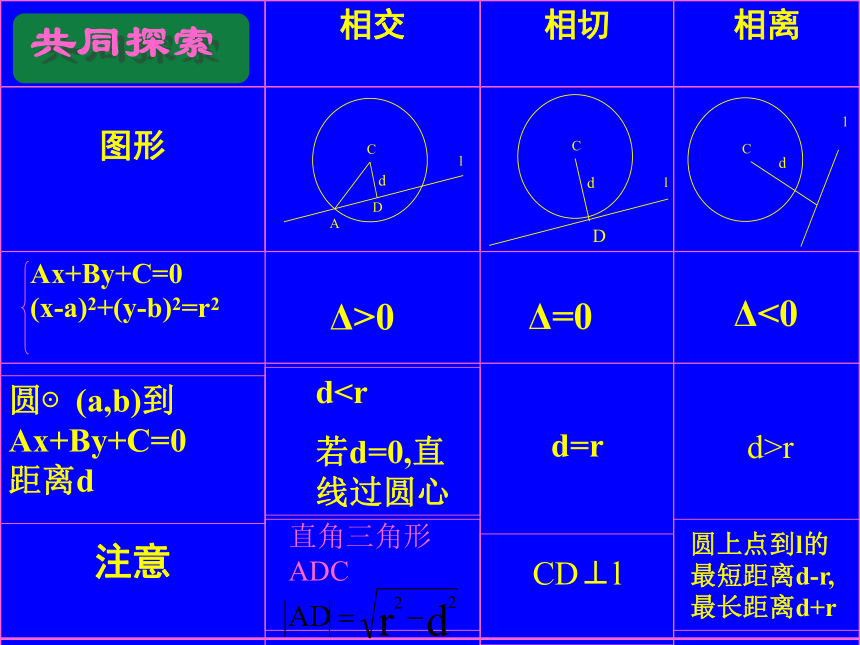
①相 交：直线与圆有两个公共点.
②相 切：直线与圆有1个公共点.
③相 离：直线与圆无公共点.得出结论：共同探索２．“想一想”2、直线l: Ax+By+C=0
与圆(x-a)2+(y-b)2=r2要动脑筋哦!共同探索Δ>0Δ=0Δ<0d若d=0,直线过圆心d=rd>rCD⊥l圆上点到l的最短距离d-r,最长距离d+r共同探索例1 已知圆方程x2+y2=2,直线y=x+b，当b为何值时，圆与直线相交、相切、相离. 解法一： x2+y2=2 ①
y=x+b ② 例 题由②代入①，x2+（x+b）2=2 2x2+2bx+b2-2=0
由线与圆相交:Δ>0 (2b)2-4×2×(b2-2)>0 　　　　　　　　　　-2由线与圆相切:Δ=0 (2b)2-4×2×(b2-2)=0 　　b=±2
由线与圆相离:Δ<0 (2b)2-4×2×(b2-2)<0 　 b>2或b<-2 例 题解法二： 圆心（0，0）半径r= 圆心到直线y=x+b距离d=例 题 |C-8|=10
C=18 或C= 2
∴ 所求直线方程3x-4y+10=0或3x-4y-10=0 例2.
求与直线3x-4y+5=0
平行且与圆x2+y2-4y=0
相切的直线的方程. 解：
设所求直线l方程为3x-4y+c=0
∵圆x2+y2-4y=0的圆心（0，2）
又l与圆相切d3x-4y+5=0例 题例 题例２还有解法吗？解：圆心到直线距离d=

圆半径为r，则dr2x-y+5=0例 题
(1)求直线3x-4y+3=0与x2+y2-6x+4y-12=0截得的弦长.
(2)求圆心在（-3，4）且与直线x-2y-4=0相切的圆方程.
(3)求圆x2+y2=1上的点到直线3x+4y-25=0的距离最大值最小值.随堂练习1.解：x2+y2-6x+4y-12=0.
(x-3)2+(y+2)2=25
∴圆心(3,-2),
半径r=5.
圆心到l:3x-4y+3=0的距离：
∴截得弦长:|AB|=2|AM|=2OXY(3,-2)AMCBrd(1)求直线3x-4y+3=0与
x2+y2-6x+4y-12=0截得的弦长。随堂练习2.解：圆与直线x-2y-4=0相切
∴圆心到直线距离d等于圆半径r
∴圆方程为:(x+3)2+(y-4)2=45 OXY(-3,4)Cd(2)求圆心在（-3，4）且与直线
x-2y-4=0相切的圆方程。随堂练习课堂小结直线l: Ax+By+C=0
与圆(x-a)2+(y-b)2=r2注意哦！相交相切
相离
完成《直线与圆的位置关系》讲义一份。作　　业谢　 　谢二OO五年十一月十五日Poyangerzhong@yahoo.com