2022-2023学年北师大版八年级数学上册2.4.2 有理数的加法(二)课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册2.4.2 有理数的加法(二)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 430.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 14:10:32 | ||
图片预览





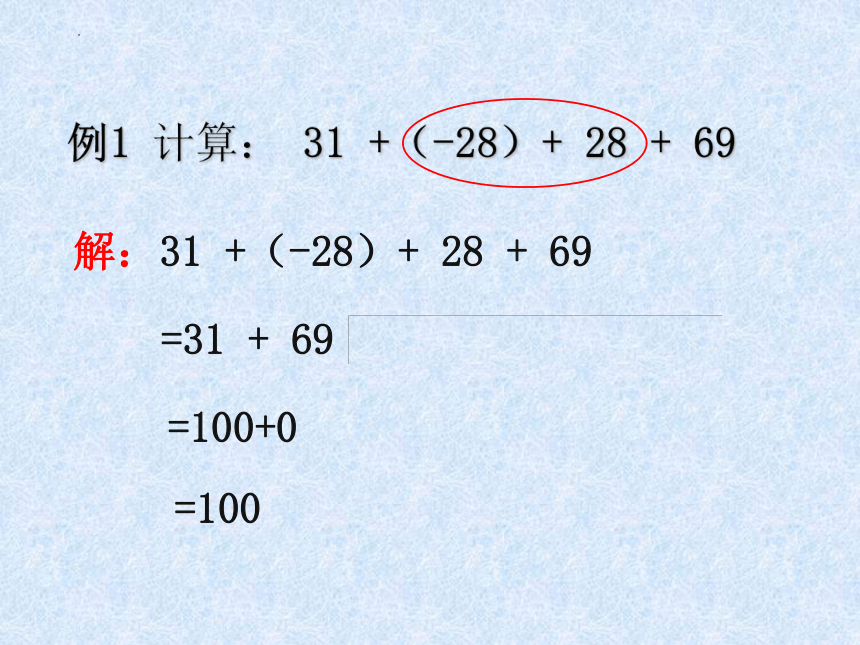
文档简介
(共19张PPT)
第二章 有理数及其运算
4 有理数的加法(二)
有理数加法法则
温故知新
同号两数相加,取 相同 符号,并把 绝对值 相加.
一个数同0相加,仍得这个数.
较小的绝对值.
取 绝对值较大的数 的符号,并用较大的绝对值 减去
异号两数相加,绝对值相等时和为 0;绝对值不等时,
例1:计算并比较每组计算结果
-17
-17
-3
-3
有理数的加法中,两个数相加,
交换加数的位置和不变.
加法交换律:
例1:计算并比较每组计算结果
-9
-9
-5
-5
有理数加法中,三个数相加,先把前两个
加法的结合律:
数相加,或者先把后两个数相加,和不变.
有理数的加法中,两个数相加,
交换加数的位置和不变.
加法交换律:a+b = b+a
有理数加法中,三个数相加,先把前两个
数相加,或者先把后两个数相加,和不变.
加法的结合律:(a+b) + c = a + (b+c)
想一想
例1 计算: 31 +(-28)+ 28 + 69
解:31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ]
=100+0
=100
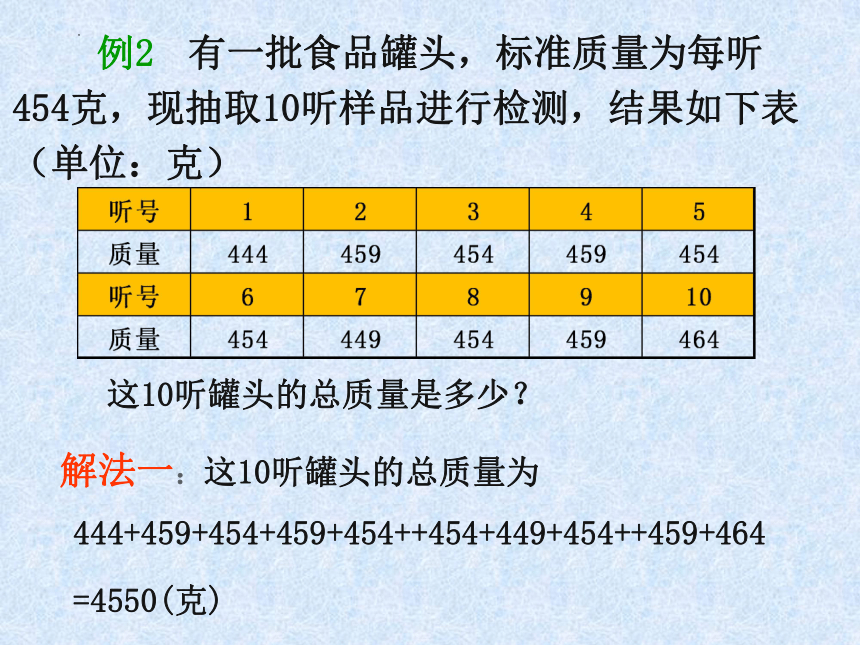
例2 有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表(单位:克)
这10听罐头的总质量是多少?
444+459+454+459+454++454+449+454++459+464
解法一:这10听罐头的总质量为
=4550(克)
这10听罐头与标准质量差值的和为
解法二:
把超过标准质量的克数用正数表示,不足的用负数表示,列出10听罐头与标准质量的差值表(单位:克):
454×10 + 10 = 4540 + 10 = 4550(克)
因此,这10听罐头的总质量为
=[(-10)+10]+[(-5)+5]+5+5=10(克)
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
+5
例3 计算:(1)15+(-23)+24+(-36)
=15+24+[(-23)+(-36)]
=39+(-59)
解:原式=
把正数与负数分别相加(同号相加),从而计算简化,这样做既运用加法交换律又运用加法的结合律
15+24
+(-23)+(-36)
=-20
(2)(-2.8)+5.6+10.8+2.4
解:原式 =
(-2.8)+10.8
=[(-2.8)+(-10.2)]+(5.6+2.4)
=(-13)+8
=-5
+5.6+2.4
能“凑整”的结合相加
(3)
解:原式=
相反数结合相加
同分母结合相加
0.5+(-0.5)
3
4
+ -
1
4
+ -
1
19
+
=0
-1
1
19
+
18
19
= -
1、 一般地,总是先把正数或负数分别结合在一起相加.
2、有相反数的可先把相反数相加,能凑整的可先凑整.
3、有分母相同的,可先把分母相同的数结合相加.
三、计算技巧
练一练
解:原式=
练一练
解:原式=
13+47
=60
练一练
解法1:原式=
43+27
=70
+(-120)
=-50
解法2:原式=
43 +(-43)
=0
+(-50)
=-50
练一练
解:原式=
1
4
1
8
+
+6 +(-6)
3
8
+ -
5
8
+ -
3
8
=
+0
+(-1)
5
8
= -
1、加法运算律从非负数范围扩大到有理数的范围.
2、掌握加法运算律的法则及公式,并适当的运用运算律进行简化计算.
三、归纳小结
1. 计算:
(1)(-3)+ 40+(-32)+(-8);
(2) 13 +(-56)+47+(-34);
(3) 43+(-77)+27+(-43).
2.某潜水员先潜入水下61米,然后又上升32米,这时潜水员处在什么位置?
四、强化训练
五、作业
P38 习题2.5
1,2,6,7
第二章 有理数及其运算
4 有理数的加法(二)
有理数加法法则
温故知新
同号两数相加,取 相同 符号,并把 绝对值 相加.
一个数同0相加,仍得这个数.
较小的绝对值.
取 绝对值较大的数 的符号,并用较大的绝对值 减去
异号两数相加,绝对值相等时和为 0;绝对值不等时,
例1:计算并比较每组计算结果
-17
-17
-3
-3
有理数的加法中,两个数相加,
交换加数的位置和不变.
加法交换律:
例1:计算并比较每组计算结果
-9
-9
-5
-5
有理数加法中,三个数相加,先把前两个
加法的结合律:
数相加,或者先把后两个数相加,和不变.
有理数的加法中,两个数相加,
交换加数的位置和不变.
加法交换律:a+b = b+a
有理数加法中,三个数相加,先把前两个
数相加,或者先把后两个数相加,和不变.
加法的结合律:(a+b) + c = a + (b+c)
想一想
例1 计算: 31 +(-28)+ 28 + 69
解:31 +(-28)+ 28 + 69
=31 + 69 + [(-28)+ 28 ]
=100+0
=100
例2 有一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,结果如下表(单位:克)
这10听罐头的总质量是多少?
444+459+454+459+454++454+449+454++459+464
解法一:这10听罐头的总质量为
=4550(克)
这10听罐头与标准质量差值的和为
解法二:
把超过标准质量的克数用正数表示,不足的用负数表示,列出10听罐头与标准质量的差值表(单位:克):
454×10 + 10 = 4540 + 10 = 4550(克)
因此,这10听罐头的总质量为
=[(-10)+10]+[(-5)+5]+5+5=10(克)
(-10)+ 5 + 0 + 5 + 0 + 0 +(-5)+ 0 + 5 + 10
+5
例3 计算:(1)15+(-23)+24+(-36)
=15+24+[(-23)+(-36)]
=39+(-59)
解:原式=
把正数与负数分别相加(同号相加),从而计算简化,这样做既运用加法交换律又运用加法的结合律
15+24
+(-23)+(-36)
=-20
(2)(-2.8)+5.6+10.8+2.4
解:原式 =
(-2.8)+10.8
=[(-2.8)+(-10.2)]+(5.6+2.4)
=(-13)+8
=-5
+5.6+2.4
能“凑整”的结合相加
(3)
解:原式=
相反数结合相加
同分母结合相加
0.5+(-0.5)
3
4
+ -
1
4
+ -
1
19
+
=0
-1
1
19
+
18
19
= -
1、 一般地,总是先把正数或负数分别结合在一起相加.
2、有相反数的可先把相反数相加,能凑整的可先凑整.
3、有分母相同的,可先把分母相同的数结合相加.
三、计算技巧
练一练
解:原式=
练一练
解:原式=
13+47
=60
练一练
解法1:原式=
43+27
=70
+(-120)
=-50
解法2:原式=
43 +(-43)
=0
+(-50)
=-50
练一练
解:原式=
1
4
1
8
+
+6 +(-6)
3
8
+ -
5
8
+ -
3
8
=
+0
+(-1)
5
8
= -
1、加法运算律从非负数范围扩大到有理数的范围.
2、掌握加法运算律的法则及公式,并适当的运用运算律进行简化计算.
三、归纳小结
1. 计算:
(1)(-3)+ 40+(-32)+(-8);
(2) 13 +(-56)+47+(-34);
(3) 43+(-77)+27+(-43).
2.某潜水员先潜入水下61米,然后又上升32米,这时潜水员处在什么位置?
四、强化训练
五、作业
P38 习题2.5
1,2,6,7
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
