2022-2023学年人教版八年级数学上册11.2.1 三角形的内角 第一课时三角形内角和定理 课件(共25张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.2.1 三角形的内角 第一课时三角形内角和定理 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 14:11:40 | ||
图片预览





文档简介
(共25张PPT)
第十一章 三角形
11.2.1 三角形的内角
义务教育课程标准实验教科书(人教版)八年级上册
第1课时 三角形内角和定理
学习目标
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形
内角和等于180°.(重点)
西沙群岛
C
B
A
40°
50°
情境引入
北
北岛
甘泉岛
北边廊
40°
50°
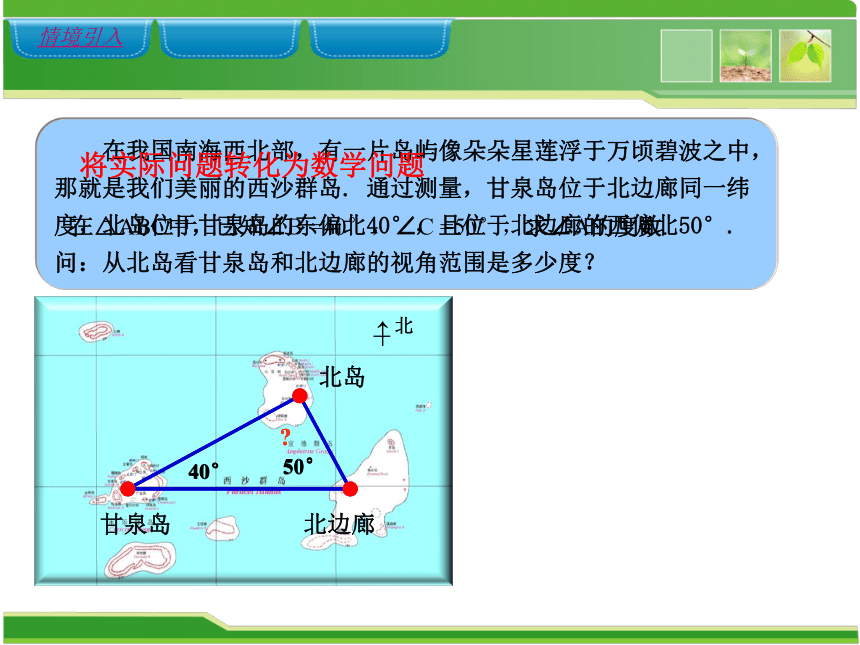
在我国南海西北部,有一片岛屿像朵朵星莲浮于万顷碧波之中,
那就是我们美丽的西沙群岛. 通过测量,甘泉岛位于北边廊同一纬
度,北岛位于甘泉岛的东偏北40°,且位于北边廊的西偏北50°.
问:从北岛看甘泉岛和北边廊的视角范围是多少度?
将实际问题转化为数学问题
在△ABC中,已知∠B =40°,∠C =50°,求∠A的度数.
↑
情境引入
新课讲授
在纸上任意画一个三角形,用量角器量出每一个内角的度数,将三角形三个内角的度数相加.
思考:三角形三个内角的和是否为定值?
在计算机上用《几何画板》软件任意画一个三角形,度量出它的各内角并计算它们的和. 然后随意改变所画三角形的形状,再量出变化后的各内角,计算内角和.由此,你能得出什么结论?
信息技术应用
情境引入
新课讲授
180°
平角
如何证明?
命题:三角形三个内角的和等于180°.
命题
定理
情境引入
新课讲授
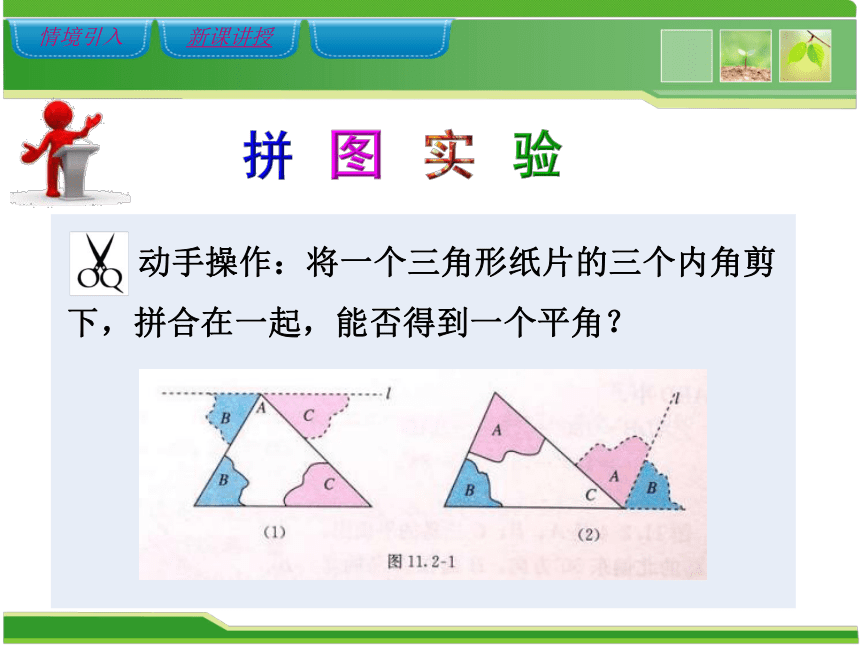
动手操作:将一个三角形纸片的三个内角剪下,拼合在一起,能否得到一个平角?
情境引入
新课讲授
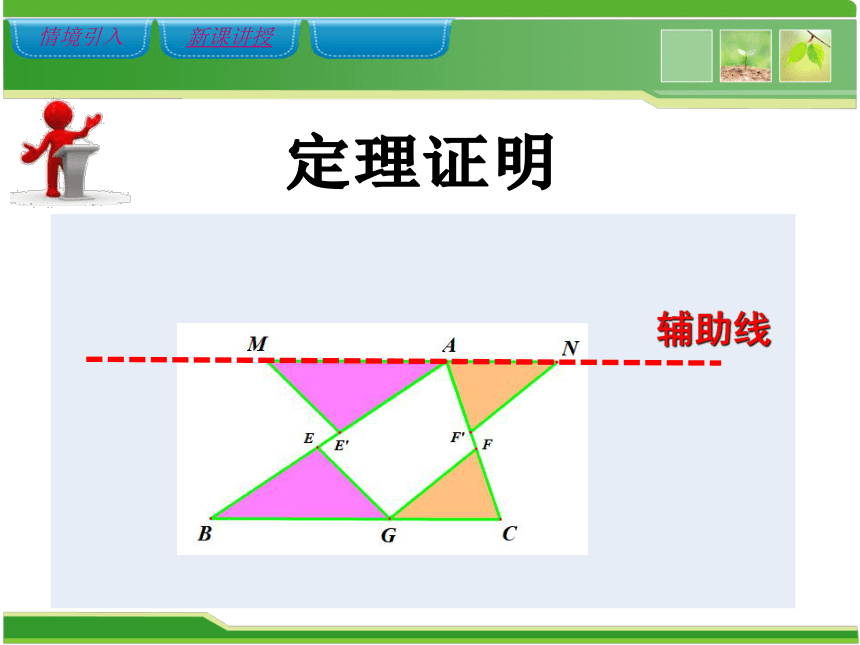
定理证明
辅助线
情境引入
新课讲授
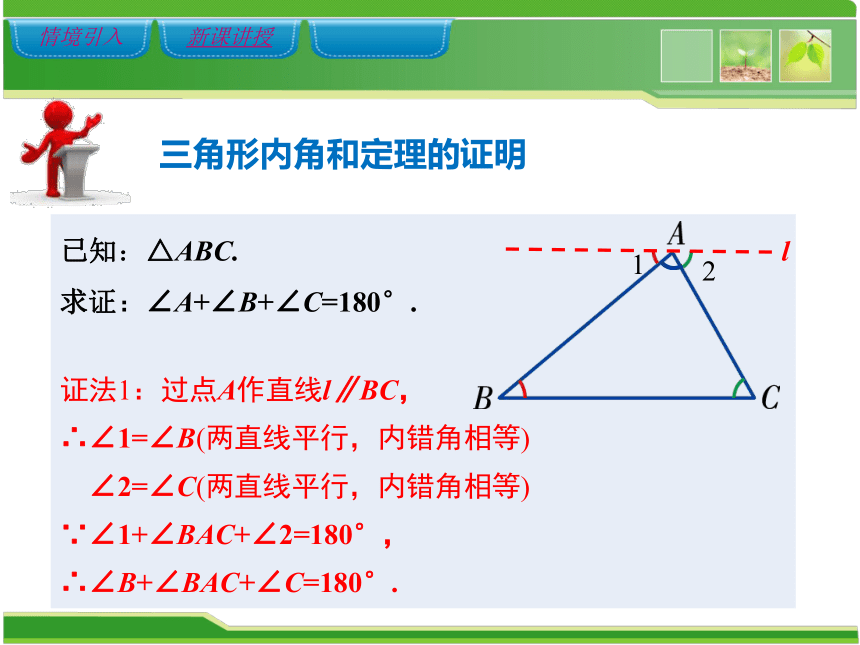
三角形内角和定理的证明
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作直线l∥BC,
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
∵∠1+∠BAC+∠2=180°,
∴∠B+∠BAC+∠C=180°.
1
2
l
情境引入
新课讲授
三角形内角和定理的证明
证法2:延长BC到D,过点C作CE∥BA,
∴∠1=∠A(两直线平行,内错角相等).
∠2=∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
情境引入
新课讲授
三角形内角和定理的证明
C
B
A
E
D
F
证法3:过点D作DE∥AC交AB于点E,
过点D作DF∥AB交DF于点E.
∴ ∠C=∠EDB,∠B=∠FDC,(两直线平行,同位角相等)
∠A=∠BED,∠BED=∠EDF,(两直线平行,内错角相等)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
想一想:同学们还有其他方法吗?
情境引入
新课讲授
思考:多种方法证明三角形内角和等于180°的
核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
情境引入
新课讲授
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
情境引入
新课讲授
在我国南海西北部,有一片岛屿像朵朵星莲浮于万顷碧波之中,
那就是我们美丽的西沙群岛. 通过测量,甘泉岛位于北边廊同一纬
度,北岛位于甘泉岛的东偏北40°,且位于北边廊的西偏北50°.
问:从北岛看甘泉岛和北边廊的视角范围是多少度?
C
B
A
40
5
40°
50°
问题解决
解:由题意知:
∠B = 40 °,∠C = 50 °
∵ 在△ABC中,∠A +∠B +∠C = 180 °
∴ ∠A = 180 °-∠B-∠C
= 180 °-40 °-50 °
= 90 °
三角形内角和定理
答:从北岛看甘泉岛和北边廊两岛的视角是90°.
新课讲授
问题解决
练习巩固
素有“天下江山第一城”的黄鹤楼是我国的AAAAA级景点,与岳
阳楼、滕王阁并称江南三大名楼. 如图,一名游客从A处观测黄鹤楼
楼顶C处的仰角∠1=30°,在B处观测C处时,仰角∠2=45°.
问:从C处观测A,B两处的视角∠ACB是多少度?
A
B
45°
1
30°
2
?
C
新课讲授
问题解决
练习巩固
45°
1
30°
2
A
C
B
法一:
解 :由题意知∠ 2 = 45 °
∵ ∠ 2+∠ CBA = 180 °(平角的定义)
∴ ∠ CBA = 180 °-∠ 2
= 180 °-45°
= 135 °
∵ 在△ABC中,∠ 1 +∠ CBA +∠ ACB = 180 °(三角形内角和定理)
∴ ∠ ACB = 180 °-∠ 1 -∠ CBA
= 180 ° - 30° - 135°
= 15 °
答:从C处观测A,B两处的视角∠ ACB为15°.
由题意,∠2=45 °
在⊿BCD中 ,
∵ ∠2+∠CDB+∠BCD=180 °(三角形内角和定理)
新课讲授
问题解决
练习巩固
法二:
45°
1
30°
2
A
C
B
D
解:过点C作CD ⊥AB交AB延长线于点D
∴ ∠BCD = 180 °-∠2 - ∠CDB
= 180 °-45° -90°
= 45 °
同理,∠ACD = 60 °
∴ ∠ACB = ∠ACD - ∠BCD
= 60 °-45° = 15 °
答:从C处观测A,B两处的视角∠ ACB为15°.
新课讲授
问题解决
练习巩固
45°
1
30°
2
A
C
B
法三:
解 :过点C作直线 l∥AB,
则∠ 3 = ∠ 1 = 30°,
∠ 4 = ∠ 2 = 45°,
(两直线平行,内错角相等)
∴ ∠ ACB = ∠ 4 -∠ 3
= 45 ° - 30°
= 15 °
l
3
4
答:从C处观测A,B两处的视角∠ ACB为15°.
问题解决
练习巩固
课堂小结
本节课你学习到了什么?
问题解决
练习巩固
课堂小结
一个定理
两类思想
两种层次
问题解决
练习巩固
课堂小结
三角形内角和定理
一个定理
三角形的三个内角的和等于180°
问题解决
练习巩固
课堂小结
(一)数学建模思想
(二)数形结合思想
两类思想
问题解决
练习巩固
课堂小结
两种层次
层次二:作辅助线证明
层次一:拼图实验
(直观)
(抽象)
练习巩固
课堂小结
作业布置
作业
P16 习题11.2
复习巩固第1题、第2题
谢 谢!
第十一章 三角形
11.2.1 三角形的内角
义务教育课程标准实验教科书(人教版)八年级上册
第1课时 三角形内角和定理
学习目标
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形
内角和等于180°.(重点)
西沙群岛
C
B
A
40°
50°
情境引入
北
北岛
甘泉岛
北边廊
40°
50°
在我国南海西北部,有一片岛屿像朵朵星莲浮于万顷碧波之中,
那就是我们美丽的西沙群岛. 通过测量,甘泉岛位于北边廊同一纬
度,北岛位于甘泉岛的东偏北40°,且位于北边廊的西偏北50°.
问:从北岛看甘泉岛和北边廊的视角范围是多少度?
将实际问题转化为数学问题
在△ABC中,已知∠B =40°,∠C =50°,求∠A的度数.
↑
情境引入
新课讲授
在纸上任意画一个三角形,用量角器量出每一个内角的度数,将三角形三个内角的度数相加.
思考:三角形三个内角的和是否为定值?
在计算机上用《几何画板》软件任意画一个三角形,度量出它的各内角并计算它们的和. 然后随意改变所画三角形的形状,再量出变化后的各内角,计算内角和.由此,你能得出什么结论?
信息技术应用
情境引入
新课讲授
180°
平角
如何证明?
命题:三角形三个内角的和等于180°.
命题
定理
情境引入
新课讲授
动手操作:将一个三角形纸片的三个内角剪下,拼合在一起,能否得到一个平角?
情境引入
新课讲授
定理证明
辅助线
情境引入
新课讲授
三角形内角和定理的证明
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作直线l∥BC,
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
∵∠1+∠BAC+∠2=180°,
∴∠B+∠BAC+∠C=180°.
1
2
l
情境引入
新课讲授
三角形内角和定理的证明
证法2:延长BC到D,过点C作CE∥BA,
∴∠1=∠A(两直线平行,内错角相等).
∠2=∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
情境引入
新课讲授
三角形内角和定理的证明
C
B
A
E
D
F
证法3:过点D作DE∥AC交AB于点E,
过点D作DF∥AB交DF于点E.
∴ ∠C=∠EDB,∠B=∠FDC,(两直线平行,同位角相等)
∠A=∠BED,∠BED=∠EDF,(两直线平行,内错角相等)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
想一想:同学们还有其他方法吗?
情境引入
新课讲授
思考:多种方法证明三角形内角和等于180°的
核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
情境引入
新课讲授
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
情境引入
新课讲授
在我国南海西北部,有一片岛屿像朵朵星莲浮于万顷碧波之中,
那就是我们美丽的西沙群岛. 通过测量,甘泉岛位于北边廊同一纬
度,北岛位于甘泉岛的东偏北40°,且位于北边廊的西偏北50°.
问:从北岛看甘泉岛和北边廊的视角范围是多少度?
C
B
A
40
5
40°
50°
问题解决
解:由题意知:
∠B = 40 °,∠C = 50 °
∵ 在△ABC中,∠A +∠B +∠C = 180 °
∴ ∠A = 180 °-∠B-∠C
= 180 °-40 °-50 °
= 90 °
三角形内角和定理
答:从北岛看甘泉岛和北边廊两岛的视角是90°.
新课讲授
问题解决
练习巩固
素有“天下江山第一城”的黄鹤楼是我国的AAAAA级景点,与岳
阳楼、滕王阁并称江南三大名楼. 如图,一名游客从A处观测黄鹤楼
楼顶C处的仰角∠1=30°,在B处观测C处时,仰角∠2=45°.
问:从C处观测A,B两处的视角∠ACB是多少度?
A
B
45°
1
30°
2
?
C
新课讲授
问题解决
练习巩固
45°
1
30°
2
A
C
B
法一:
解 :由题意知∠ 2 = 45 °
∵ ∠ 2+∠ CBA = 180 °(平角的定义)
∴ ∠ CBA = 180 °-∠ 2
= 180 °-45°
= 135 °
∵ 在△ABC中,∠ 1 +∠ CBA +∠ ACB = 180 °(三角形内角和定理)
∴ ∠ ACB = 180 °-∠ 1 -∠ CBA
= 180 ° - 30° - 135°
= 15 °
答:从C处观测A,B两处的视角∠ ACB为15°.
由题意,∠2=45 °
在⊿BCD中 ,
∵ ∠2+∠CDB+∠BCD=180 °(三角形内角和定理)
新课讲授
问题解决
练习巩固
法二:
45°
1
30°
2
A
C
B
D
解:过点C作CD ⊥AB交AB延长线于点D
∴ ∠BCD = 180 °-∠2 - ∠CDB
= 180 °-45° -90°
= 45 °
同理,∠ACD = 60 °
∴ ∠ACB = ∠ACD - ∠BCD
= 60 °-45° = 15 °
答:从C处观测A,B两处的视角∠ ACB为15°.
新课讲授
问题解决
练习巩固
45°
1
30°
2
A
C
B
法三:
解 :过点C作直线 l∥AB,
则∠ 3 = ∠ 1 = 30°,
∠ 4 = ∠ 2 = 45°,
(两直线平行,内错角相等)
∴ ∠ ACB = ∠ 4 -∠ 3
= 45 ° - 30°
= 15 °
l
3
4
答:从C处观测A,B两处的视角∠ ACB为15°.
问题解决
练习巩固
课堂小结
本节课你学习到了什么?
问题解决
练习巩固
课堂小结
一个定理
两类思想
两种层次
问题解决
练习巩固
课堂小结
三角形内角和定理
一个定理
三角形的三个内角的和等于180°
问题解决
练习巩固
课堂小结
(一)数学建模思想
(二)数形结合思想
两类思想
问题解决
练习巩固
课堂小结
两种层次
层次二:作辅助线证明
层次一:拼图实验
(直观)
(抽象)
练习巩固
课堂小结
作业布置
作业
P16 习题11.2
复习巩固第1题、第2题
谢 谢!
