人教版数学七年级上册第一章 有理数 课件(共134张PPT)
文档属性
| 名称 | 人教版数学七年级上册第一章 有理数 课件(共134张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 14:07:57 | ||
图片预览










文档简介
(共134张PPT)
人教版数学七年级上册
第一章 有理数课件
正数和负数(一)
合作学习:课本P2 观察1和2
问题一:上述介绍中有小学学过哪些数? 你能按照某一标准将它们分类?
整数:0、1、2、3……
分数(小数):1/2、0.36、5%……
欢迎新同学
自我介绍:姓名、年龄、身高等
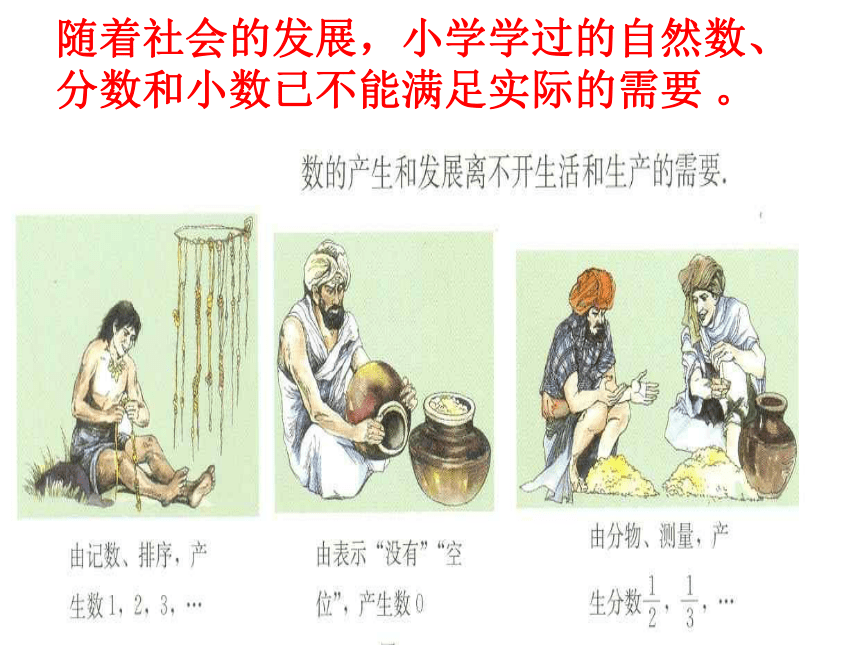
数的产生和发展离不开生活和生产的需要
随着社会的发展,小学学过的自然数、分数和小数已不能满足实际的需要 。
1.1正数和负数(一)
合作学习:课本P2 观察1和2
长丰县城东中学 冯东
我们把以前学过的数大于零叫做 正数。有时在正数前面也加上“+”(正)号。 如+0.5、+3、+1/2……“+”号可以省略。
我们把在以前学过的数(0除外)前面加上负号“-”的数叫做负数。如-3、-0.5、-2/3……
概念引入
一个数前面的“+”、“-”号叫做它的符号。 “-”号读着“负”,如:“-5”读着“负5”;“+”号读着“正”,如:“+3”读着“正3”。“+”号可以省略。
说一说存折上的数各表示什么?
你能举出生活中具有相反意义的例子吗?例子里要有正数和负数。
在下列横线上填上适当的词,使前后构成意义相反的量:
(1)收入1300元, 800元;
(2) 80米,下降64米;
(3)向北前进30米, 50米.
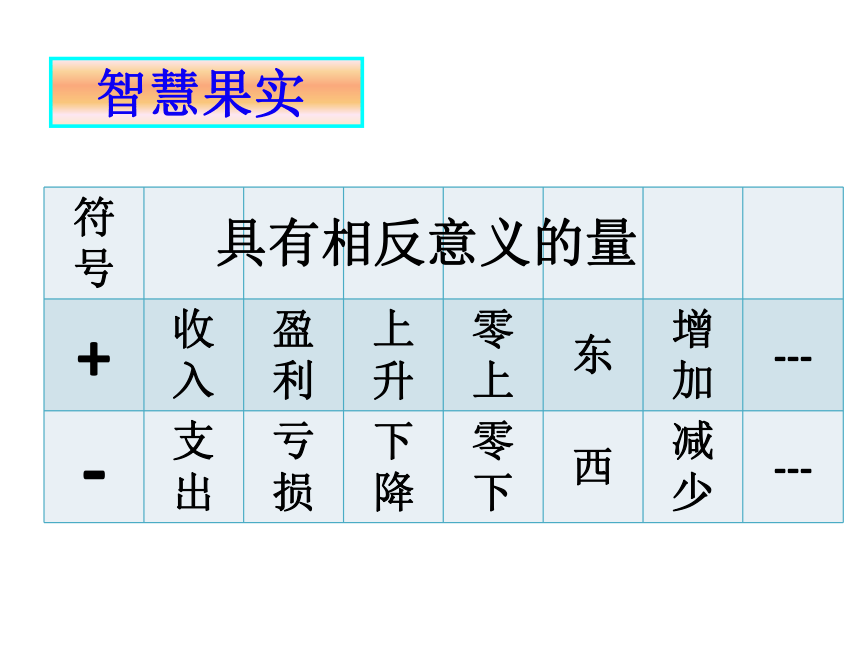
智慧果实
符号
+ 收入 盈利 上升 零上 东 增加 ---
- 支出 亏损 下降 零下 西 减少 ---
具有相反意义的量
一、正负数可以用现实生活中具有相反意义的量来解释。
1、如果将+8元计为收入8元,则-6元表示 _______ 。
2、高出海平面789米计为+789米,则-789米表示__ _____ 。
3、减少60千克计为-60千克,则+80千克表示 ______ 。
4、把公元2012年记作+2012年,那么-221年表示 _______。
支出6元
低于海平面789米
增加80千克
公元前221年
随堂练习
二、读下列各数,并指出其中哪些是正数,哪些是负数。
-1, 2.5,+ , 0 ,-3.14,
120, - , -1.732
一个数不是正数就是负数,对吗?
0既不是正数也不是负数。0是正负数的分界。
问题思考
0只表示没有吗
1.空罐中的金币数量;
2.温度中的0℃;
3.海平面的高度;
4.标准水位;
5.身高比较的基准;
6.正数和负数的界点;
……引入正负数后,0不再简简单单的只表示没有.
它具有丰富的意义,是正负数的基准。
10℃表示白天温度为零上10℃,-5℃表示晚上温度为零下5℃。
它们以什么为基准?
2、若将28计为0,则可将27计为-1,试猜想若将 27计为0,28应计为 。
1、东、西为两个相反方向,如果- 4米表示一物体向西运动4米,那么+2米表示什么?物体原地不动记为什么?
拓展练习
3、观察下列排列的每一列数,研究它的排列有什么规律 并填出空格上的数.
(1)1,-2,1,-2,1,-2, , , ,…
(2)-2,4,-6,8,-10, , , ,…
(3)1,0,-1,1,0,-1, , , ,…
1、这节课你学会了什么
2、你还有什么不懂的吗?
课堂总结
课本 习题1.1 第1,3题
课堂作业
寻找回忆
什么叫做相反数?
你能找出互为相反数的两个数在数轴上表示的点的共同特点吗?
1.2.4 绝 对 值
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,(absolute value)。
想一想 互为相反数的两个数的绝对值有什么关系?
提示:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。
想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数,负数和0
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
A
B
的绝对值是
记作
做一做
写出下列各数的绝对值:
解:
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
判断:
(1)一个数的绝对值是 2 ,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。
(5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
2、已知有理数a在数轴上对应的点如图所示:
则|a| =________
4、如果a 的相反数是-0.74,那么|a| =______
3. 如果一个数的绝对值等于3.25 ,则这个数是___
5. 如果|x-1|=2,则x=______.
课堂升华
a
0
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2,
3,(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
课后作业:
P14 4
P15 4
目标: P5
(1)求绝对值不大于2的整数;
(2)已知x是整数,且2.5<|x|<7, 求x.
思考
人教版新课标七年级上册
课题:有理数加减
数轴、相反数、绝对值……
计算
有理数的加法
有理数的加法
121+57=178
121
+
57
178
有理数的加法
(+3)+(+4)=+7
(-3)+(-4)=-7
(-3)+(+4)=+1
(+3)+(-4)=-1
(-3)
(-3)
(-4)
(-4)
有理数的加法
正
(+3)
(+4)
(+3)+(+4)=+7
有理数的加法
负
(-3)
(-4)
(-3)+(-4)=-7
同号两数相加,取相同的符号,
并把绝对值相加.
(+3)+(+4)=+7
(-3)+(-4)=-7
有理数的加法
(2) (-3)+(-9)
= -(3+9)= -12
练一练
(3) (-13)+(-8)
= -(13+8)= -21
(1) 6 + 11
= +(6+11)= 17
(1) 6 + 11
(2)(-3)+(-9)
(3)(-13)+(-8)
解:
有理数的加法
(+4)
(-3)
+1
(+4)+(-3)=+1
(+9)+(-3)=+6
有理数的加法
(+4)
(-5)
-1
(-5)+(+4)=-1
(-9)+(+4)=+5
有理数的加法
(+4)+(-3)=+1
(-5)+(+4)=-1
绝对值不相等的异号两数相加,
取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
(1) (-3)+ 9
= +(9-3)= 6
练一练
(2) 10 + (-6)
= +(10-6) = 4
(1) (-3)+ 9
(2) 10 + (-6)
解:
有理数的加法
1、先判断类型(同号、异号等);
2、再确定和的符号;
3、后进行绝对值的加减运算。
运算步骤:
计算:
例1
有理数的加法
有理数的加法
通过本节课学习,我们应该掌握:
一、有理数的加法法则
二、我学会了……
使我感触最深的是……
我发现生活中……
我还感到疑惑的是……
小结:
有理数的加法
作业:课本P24页习题1.3第一题
感
谢
聆
听
~
1.4有理数的乘除法
2、如果3分钟以后记为+3分钟,那么3分钟以前应该记为 。
1、如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 。
-2cm
-3min
教材知识点梳理
一、有理数乘法
问题铺垫
l
O
如图,有一只蜗牛沿直线 l 爬行,它现在的位置恰好在l 上的一点O。
1、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
4、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
3、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
教材知识点梳理
一、有理数乘法
O
2
4
6
8
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它在点O的 边 cm处?
每分钟2cm的速度向右记为 ; 3分钟以后记为 。
其结果可表示为 。
右
6
+2
+3
(+2)×(+3)=+6
教材知识点梳理
一、有理数乘法
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,3分钟后它在点O的 边 cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向左记为 ; 3分钟以后记为 。
其结果可表示为 。
-2
+3
(-2)×(+3)=-6
教材知识点梳理
一、有理数乘法
想一想:
问题2的结果(-2)×(+3)=-6与问题1的结果(+2)×(+3)=+6有何区别?
结论: 两个有理数相乘,改变其中一个因数的符号,积的符号也随之改变。
教材知识点梳理
一、有理数乘法
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处, 3分钟前它在点O的 边 cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向右记为 ; 3分钟以前记为 。
其结果可表示为 。
+2
-3
(+2)×(-3)=-6
教材知识点梳理
一、有理数乘法
问题一: 如果蜗牛一直以每分2cm的速度向 左爬行,现在蜗牛在点O处, 3分钟前它在点O 边 cm处?
O
2
4
6
8
右
6
每分钟2cm的速度向左记为 ; 3分钟以前记为 。
其结果可表示为 。
-2
-3
(-2)×(-3)=+6
教材知识点梳理
一、有理数乘法
想一想:
问题4的结果(-2)×(-3)=+6与问题1的结果(+2)×(+3)=+6有何区别?
结论: 两个有理数相乘,同时改变两个因数的符号,积的符号不变。
教材知识点梳理
一、有理数乘法
(+2)×(+3) = +6
(-2)×(+3)= -6
(+2)×(-3)= -6
(-2)×(-3)= +6
正数乘以正数积为 数
负数乘以正数积为 数
正数乘以负数积为 数
负数乘以负数积为 数
乘积的绝对值等于各因数绝对值的 。
规律呈现:
正
负
负
正
积
教材知识点梳理
一、有理数乘法
问题三:如果蜗牛一直以每分钟2cm的速度向右爬行,0分钟后它在什么位置?
O
2
4
6
8
问题六:如果蜗牛一直以每分钟0cm的速度向左爬行,3分钟前它在什么位置?
O
-8
-6
-4
-2
结论: 2×0= 0
结论: 0×(-3)= 0
教材知识点梳理
一、有理数乘法
乘法算式
因数特征
积的特征
(-2)×(-3)=+6
(+2)×(+3)=+6
(+2)×(-3)=-6
(-2)×(+3)=-6
(+2)×0=0
0×(-3)=0
同号
异号
一个因数为0
得正
得负
得 0
教材知识点梳理
一、有理数乘法
法则的应用:
(-5)×(-3)
(-7)×4
= +
= 15
(5 × 3)
= -
(7 × 4)
= -28
有理数相乘,先确定积的符号,再确定积的绝对值。
教材知识点梳理
一、有理数乘法
1 计算:
(1)(-3) × 9
(2)(- )×(-2)
解:
(1)(-3) × 9 = -(3 × 9 ) = -27
(2)(- )×(-2)= +( × 2 )= 1
知识点及时练
小试牛刀
(1) 6 × (- 9)
(3)(- 6)×(- 1)
(4)(- 6)× 0
(2)(- 15) ×
(5) 4 ×
(6) ×
(7)(- 12)×(- )
(8)(- 2 )×(- )
知识点及时练
结论:乘积是1的两个数互为倒数
1的倒数为
-1的倒数为
的倒数为
- 的倒数为
5的倒数为
-5的倒数为
的倒数为
- 的倒数为
1
-1
3
-3
-3
-3
教材知识点梳理
观察下列各式,它们的积是正的还是负的还是0
观察归纳
(1)2×3×4×(-5)
(2)2×3×(-4)×(-5)
(3)2×(-3)×(-4)×(-5)
(4)(-2)×(-3)×(-4)×(-5)
积是 .
积是 .
积是 .
积是 .
负
负
正
正
(5) (-3 )×0×(-4)×(-5)
积是 .
0
思考:积的正负与什么因数的个数有关
教材知识点梳理
一、有理数乘法
算一算:
(1)3×(-2)×(-4)
(2)(-2)×3×(+4)
(3)(-6)×(-5)×(-7)
(4)(-6)×0×(-8.1)×(-7.8)
=24
=-24
=-210
=0
思考:积的正负与什么因数的个数有关
教材知识点梳理
一、有理数乘法
几个不是0的数相乘,
负因数的个数是偶数时,积是正数
负因数的个数是奇数时,积是负数
并把各个因数的绝对值相乘。
认真记呦!
新知识
几个数相乘,如果其中有因数为0,那么积等于0。
教材知识点梳理
一、有理数乘法
1.填空(用>,<,= 填空)
(1)(-1)×2×(-3) 0
(2)(-7)×(-0.5)×(-3) 0
(3)(-4)×(-3)×|-2| 0
(4)5×(-6)×(-7)×0 0
>
>
<
=
知识点及时练
2.口算
(1)(-2)×3×4×(-1)
(2)(-5)×(-3)×4×(-2)
(3)(-2)×(-2)×(-2)×(-2)
(4)(-3)×(+3)×(-3)×(-3)
=24
=-120
=16
=-81
知识点及时练
3.计算
知识点及时练
解:原式=
知识点及时练
确定符号
绝对值相乘
解:原式=
确定符号
绝对值相乘
知识点及时练
第一组:
(2) (3×4)×0.25= 3×(4×0.25)=
(3) 2×(3+4)= 2×3+2×4=
(1) 2×3= 3×2=
思考:上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
教材知识点梳理
一、有理数乘法
5×(-4) =
15 - 35
第二组:
(2) [3×(-4)]×(- 5)=
3×[(-4)×(-5)]=
(3) 5×[3+(-7 )]=
5×3+5×(-7 ) =
(1) 5×(-6) = (-6 )×5=
-30
-30
60
60
-20
-20
5× (-6) (-6) ×5
[3×(-4)]×(- 5) 3×[(-4)×(-5)]
5×[3+(-7 )] 5×3+5×(-7 )
=
=
=
(-12)×(-5) =
3×20=
教材知识点梳理
一、有理数乘法
思考:
(1)第一组式子中数的范围是 ________;
(2)第二组式子中数的范围是 ________;
(3)比较第一组和第二组中的算式,可以发现______________________________________.
正数
有理数
各运算律在有理数范围内仍然适用
教材知识点梳理
一、有理数乘法
教材知识点梳理
一、有理数乘法
两个数相乘,交换两个因数的位置,积相等.
ab=ba
乘法交换律:
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
乘法结合律:
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:
a(b+c)
ab+ac
=
( + - )×12
用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=- 1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
= 3 + 2- 6
=- 1
知识点及时练
下列各式中用了哪条运算律?如何用字母表示?
(1)(-4)×8 = 8 ×(-4)
(2)[(-8)+5]+(-4)=(-8)+[5+(-4)]
(3) (-6)×[-+(- -)]=(-6)×- +(-6)×(- -)
(4)[29×(- - )] ×(-12)=29 ×[(- -)×(-12)]
(5) (-8)+(-9)=(-9)+(-8)
乘法交换律: ab=ba
分配律:a(b+c)=ab+ac
乘法结合律: (ab)c = a(bc)
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
2
3
1
2
1
2
2
3
5
6
5
6
知识点及时练
知识点及时练
① (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
② 60×(1- - - )
1
2
1
3
1
4
③ (- )×(8-1 -4 )
3
4
1
3
④ (-11)×(- )+(-11)×2 +(-11)×(- )
2
5
3
5
1
5
① -0.4
②-5
③-2
④-22
知识点及时练
这题有错吗?错在哪里?
想一想
(-24)×( - + - )
5
8
1
6
3
4
1
3
解:
原式=
-24× -24× +24× - 24×
5
8
1
6
3
4
1
3
计算:
= - 8 -18 +4- 15
= - 41 +4
= - 37
正确解法:
特别提醒:
1.不要漏掉符号,
2.不要漏乘.
_____ ______ ______ ______
上一页
下一页
想一想
(-24)×( - + - )
5
8
1
6
3
4
1
3
计算:
= - 8 + 18 - 4 + 15
= - 12 +33
= 21
=(-24)× +(-24)×(- )+(-24)× +(-24)×(- )
1
3
3
4
1
6
5
8
知识点及时练
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期一 星期三 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
如何求这周每天上午8时的平均气温?
即 (-14)÷7
教材知识点梳理
二、有理数的除法
教材知识点梳理
二、有理数的除法
填一填
a -5 1 -1 0
a的倒数
6
1
-1
0.5
2
/
教材知识点梳理
二、有理数的除法
1、(-2) ×7=___
-14
除法是乘法的逆运算
(-14)÷7=___
-2
2、(-2)×(-4)=___
8
8÷ (-4)=___
-2
-2
-2
★
★
◆
◆
-6
-3
填空并思考:
(-3)× 2= ____
(-3)× (- 2 ) = ____
6
-2
6÷ (-3)= ___
(-6) ÷ 2= ___
你有新的发现吗?
(-6) × =
6 ×( )=
另外:
-3
-2
(-6) ÷ 2= (-6)×
6÷(-3)= 6 ×( )
教材知识点梳理
二、有理数的除法
除法可以转化为乘法
要注意两个变化!!
(1)除号变为乘号
(2)除数变为它的倒数
除以一个(不等于零)数,等于乘以这个数的倒数.
一般地,有理数的乘法与除法之间有以下关系:
教材知识点梳理
二、有理数的除法
有理数除法法则(一)
。
1)两个有理数相除,同号得_____,异号得______,并把绝对值_____。
有理数除法法则(二):
正
负
相除
0
2)0除以任何非0的数都是_____。
0 ÷5=
= 0
0 ÷(-5)=
= 0
教材知识点梳理
二、有理数的除法
法则1:除以一个不等于0的数,等于乘这个数的倒数.
法则2:两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0.
有理数的除法法则
1 计算: (1) (- 36) ÷9 ;
(2) ÷( ).
=
× ( )
=
解: (1) (-36) ÷9 = - 36 ÷9 = - 4;
(2) ( )
÷
对于这两题的计算,你有什么样的思路?
如果两数相除,能够整除就选择法则2,不能够整除就选择用法则1.
-
知识点及时练
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
2:化简下列各式:
知识点及时练
3,计算:
(1)
(2)
1除以一个不为零的数的商就是这个数的倒数.
解:
解:
知识点及时练
4.计算
(1)
解
(2)
(1)有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算
(2)乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
知识点及时练
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
教材知识点梳理
三、一则混合运算
混合运算的顺序
这个解法是正确的
这个解法是错误的
练习、观察下面两位的解法正确吗?若不正确,你能发现下面解法问题出在哪里吗?
知识点及时练
练习、观察下面两位同学的解法正确吗?若不正确,你能发现下面解法问题出在哪里吗?
这个解法是错误的
这个解法是正确的
还有更好的解法吗?
知识点及时练
练习、请你仔细阅读下列材料:
按常规方法计算
知识点及时练
再根据你对所提供材料的理解,选择合适的方法计算:
简便计算,先其倒数
计算(-4) ÷2,4 ÷(-2),(-4) ÷(-2).
联系这类具体的数的除法,你认为a,b是有理数,b≠0,下列式子是否成立 从它们可以总结什么规律
(1) ,(2)中的式子都成立.从它们可以总结出:分子,分母以及分数这三者的符号,改变其中的两个,分数的值不变.
(1)边长为a的正方形的面积如何表示?
(2)棱长为a的正方体的体积如何表示?
记作
记作
读作:a的平方(a的二次方)
读作:a的立方(a的三次方)
4个a相乘呢?
5个a相乘呢?
100个a相乘呢?
猜想:
问题
一般地,几个相同的因数a 相乘,即
记作: 。
读作:a的n次方
求n个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
运算
乘方
结果
幂
也可读作a的n次幂
教材知识点梳理
六、乘方
本讲之后你应该学会
1.掌握有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘
任何数与0相乘,都得0
乘积是1的两个数互为倒数
同正异负
本讲之后你应该学会
2.能用法则正确地进行有理数乘法运算
例: (1)(-3)×9;(2)8×(-1)
本讲之后你应该学会
3.能确定多个因数相乘时,积的符号,并能用法则进行多个因数的乘积运算
例:(-0.5) ×(-1) ×( - )×(-8)
本讲之后你应该学会
4.能用乘法的三个运算律来进行乘法的简化运算
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
( + - )×12
例: 用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=- 1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
= 3 + 2- 6
=- 1
本讲之后你应该学会
本讲之后你应该学会
5.掌握有理数除法法则
除以一个不等于0的数,等于乘以这个数的倒数
两数相除,同号得正,异号得负,并把绝对值相除,0除以任何一个不等于0的数,都得0.
转化的思想
本讲之后你应该学会
6.会进行有理数的除法运算以及分数的化简
例:
本讲之后你应该学会
7.掌握有理数的加减乘除混合运算
有理数的乘方
棋盘上的学问
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
退出
下一页
上一页
返回
第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
退出
上一页
下一页
有一张厚度是0.1毫米的纸,将它对折50次后,请想象厚度有多高?
⑴ 对折2次后,厚度为多少毫米?
2×2×1
⑵ 对折3次后,厚度为多少毫米?
2×2×2×1
⑶ 对折4次后,厚度为多少毫米?
2×2×2×2×1
⑷ 对折50次后,厚度为多少毫米?
2×2×2×…×2×1
当要表示多个相同因数相乘时,以上写法多麻烦啊!有没有简便写法呢?
退出
上一页
下一页
小学我们学过一个数的平方和立方
2×2=
2×2×2=
则2×2×2×2=____
(-3) × (-3) × (-3) × (-3) × (-3)=
a.a.a.a.a.a.=
=
退出
上一页
下一页
个相同的因数 相乘,即
我们把它作 ;
即
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
底数
因数
指数
因数的个数
读作 的 次方,也可以读作 的 次幂。
幂
幂
幂
幂
幂
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
底数
因数
底数
因数
底数
因数
底数
因数
底数
因数
相同因数
相同因数
相同因数
相同因数
相同因数
退出
上一页
下一页
返回
乘方的读法
1、a的n次方
2、a的n次幂
返回
下一页
上一页
退出
练练吧一
1)在 中,12是 数,10是
数,读作 ;
表示:
2) 的底数是 ,指数是 ,读作
;
底
指
12的10次方或12的10次幂
的7次方
7
10个12 相乘
退出
上一页
下一页
返回
3、在 中,-3是 数,
16是 数,读作 ;
4、在 中,底数是 ;指数是 ;
读作 ;
底
-3的16次方
指
17
的17次方
返回
下一页
上一页
退出
(5)5看成幂的话,底数是 ,指数是 ,可读作 ;
(6) a 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
5
1
5的一次方
1
的一次方
退出
上一页
下一页
返回
练练吧二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
退出
上一页
下一页
返回
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
下一页
上一页
退出
返回
练练吧三: 计算
(1)102 103
(2)
=100
=1000
=10000
=100
=-1000
=10000
(3)
=0.01
=0.001
=0.0001
=0.00001
(4)(-0.1) (-0.1) (-0.1) (-0.1)
=0.01
=-0.001
观察计算的结果,你发现了什么规律?
=0.0001
=-0.00001
(-10)
=-100000
10
=100000
10
规律:
(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
(2)底数绝对值为10的幂的特点:1后面0的个数与指数相同。
(3)底数绝对值为0.1的幂的特点:1前面0的个数与指数相同(包括小数点前的1个零。
猜一猜
知识探索
例1、比较下列各数的值。它们一样吗?
1、 和
2、 , 和
解:1、
3、 = ;
注意到指数的位置与运算值的关系了吗?
退出
上一页
下一页
返回
2、
注意乘方中括号,负号的位置哦
思考:用乘方式子怎么表示 的相反数?
返回
下一页
上一页
退出
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
口答
1、 是 (填“正”或“负”)数;
2、 是 (填“正”或“负”)数;
3、 是 (填“正”或“负”)数;
是 (填“正”或“负”)数;
= (n不等于0);
正
负
正
1
负
退出
上一页
下一页
返回
练练吧四:
计算
(1) (2) (3)
(4) (5) (6)
(7) (8) (9)
(10)
1
1
-1
-1
0的任何次幂都得0
退出
上一页
下一页
返回
同学们,现在我们可以解决开始时的《棋盘上的学问》上的问题了吗?
退出
上一页
下一页
返回
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616
读一读
棋盘上的学问
知识梳理
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;
2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数 的偶次幂是正数;
3、进行乘方运算应先定符号后计算。
4、0和1的任何次幂都它本身
退出
上一页
下一页
返回
课后测验
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。
4
6
-4的7次方或-4的7次幂
负
-8
0
退出
上一页
下一页
返回
人教版数学七年级上册
第一章 有理数课件
正数和负数(一)
合作学习:课本P2 观察1和2
问题一:上述介绍中有小学学过哪些数? 你能按照某一标准将它们分类?
整数:0、1、2、3……
分数(小数):1/2、0.36、5%……
欢迎新同学
自我介绍:姓名、年龄、身高等
数的产生和发展离不开生活和生产的需要
随着社会的发展,小学学过的自然数、分数和小数已不能满足实际的需要 。
1.1正数和负数(一)
合作学习:课本P2 观察1和2
长丰县城东中学 冯东
我们把以前学过的数大于零叫做 正数。有时在正数前面也加上“+”(正)号。 如+0.5、+3、+1/2……“+”号可以省略。
我们把在以前学过的数(0除外)前面加上负号“-”的数叫做负数。如-3、-0.5、-2/3……
概念引入
一个数前面的“+”、“-”号叫做它的符号。 “-”号读着“负”,如:“-5”读着“负5”;“+”号读着“正”,如:“+3”读着“正3”。“+”号可以省略。
说一说存折上的数各表示什么?
你能举出生活中具有相反意义的例子吗?例子里要有正数和负数。
在下列横线上填上适当的词,使前后构成意义相反的量:
(1)收入1300元, 800元;
(2) 80米,下降64米;
(3)向北前进30米, 50米.
智慧果实
符号
+ 收入 盈利 上升 零上 东 增加 ---
- 支出 亏损 下降 零下 西 减少 ---
具有相反意义的量
一、正负数可以用现实生活中具有相反意义的量来解释。
1、如果将+8元计为收入8元,则-6元表示 _______ 。
2、高出海平面789米计为+789米,则-789米表示__ _____ 。
3、减少60千克计为-60千克,则+80千克表示 ______ 。
4、把公元2012年记作+2012年,那么-221年表示 _______。
支出6元
低于海平面789米
增加80千克
公元前221年
随堂练习
二、读下列各数,并指出其中哪些是正数,哪些是负数。
-1, 2.5,+ , 0 ,-3.14,
120, - , -1.732
一个数不是正数就是负数,对吗?
0既不是正数也不是负数。0是正负数的分界。
问题思考
0只表示没有吗
1.空罐中的金币数量;
2.温度中的0℃;
3.海平面的高度;
4.标准水位;
5.身高比较的基准;
6.正数和负数的界点;
……引入正负数后,0不再简简单单的只表示没有.
它具有丰富的意义,是正负数的基准。
10℃表示白天温度为零上10℃,-5℃表示晚上温度为零下5℃。
它们以什么为基准?
2、若将28计为0,则可将27计为-1,试猜想若将 27计为0,28应计为 。
1、东、西为两个相反方向,如果- 4米表示一物体向西运动4米,那么+2米表示什么?物体原地不动记为什么?
拓展练习
3、观察下列排列的每一列数,研究它的排列有什么规律 并填出空格上的数.
(1)1,-2,1,-2,1,-2, , , ,…
(2)-2,4,-6,8,-10, , , ,…
(3)1,0,-1,1,0,-1, , , ,…
1、这节课你学会了什么
2、你还有什么不懂的吗?
课堂总结
课本 习题1.1 第1,3题
课堂作业
寻找回忆
什么叫做相反数?
你能找出互为相反数的两个数在数轴上表示的点的共同特点吗?
1.2.4 绝 对 值
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,(absolute value)。
想一想 互为相反数的两个数的绝对值有什么关系?
提示:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的。
想一想 这里的数a可以表示什么样的数?
这里的数a可以是正数,负数和0
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
A
B
的绝对值是
记作
做一做
写出下列各数的绝对值:
解:
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成:
(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
判断:
(1)一个数的绝对值是 2 ,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。
(5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
2、已知有理数a在数轴上对应的点如图所示:
则|a| =________
4、如果a 的相反数是-0.74,那么|a| =______
3. 如果一个数的绝对值等于3.25 ,则这个数是___
5. 如果|x-1|=2,则x=______.
课堂升华
a
0
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
2,
3,(1)如果a>0,那么|a|=a
(2)如果a<0,那么|a|=-a
(3)如果a=0,那么|a|=0
课后作业:
P14 4
P15 4
目标: P5
(1)求绝对值不大于2的整数;
(2)已知x是整数,且2.5<|x|<7, 求x.
思考
人教版新课标七年级上册
课题:有理数加减
数轴、相反数、绝对值……
计算
有理数的加法
有理数的加法
121+57=178
121
+
57
178
有理数的加法
(+3)+(+4)=+7
(-3)+(-4)=-7
(-3)+(+4)=+1
(+3)+(-4)=-1
(-3)
(-3)
(-4)
(-4)
有理数的加法
正
(+3)
(+4)
(+3)+(+4)=+7
有理数的加法
负
(-3)
(-4)
(-3)+(-4)=-7
同号两数相加,取相同的符号,
并把绝对值相加.
(+3)+(+4)=+7
(-3)+(-4)=-7
有理数的加法
(2) (-3)+(-9)
= -(3+9)= -12
练一练
(3) (-13)+(-8)
= -(13+8)= -21
(1) 6 + 11
= +(6+11)= 17
(1) 6 + 11
(2)(-3)+(-9)
(3)(-13)+(-8)
解:
有理数的加法
(+4)
(-3)
+1
(+4)+(-3)=+1
(+9)+(-3)=+6
有理数的加法
(+4)
(-5)
-1
(-5)+(+4)=-1
(-9)+(+4)=+5
有理数的加法
(+4)+(-3)=+1
(-5)+(+4)=-1
绝对值不相等的异号两数相加,
取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值.
(1) (-3)+ 9
= +(9-3)= 6
练一练
(2) 10 + (-6)
= +(10-6) = 4
(1) (-3)+ 9
(2) 10 + (-6)
解:
有理数的加法
1、先判断类型(同号、异号等);
2、再确定和的符号;
3、后进行绝对值的加减运算。
运算步骤:
计算:
例1
有理数的加法
有理数的加法
通过本节课学习,我们应该掌握:
一、有理数的加法法则
二、我学会了……
使我感触最深的是……
我发现生活中……
我还感到疑惑的是……
小结:
有理数的加法
作业:课本P24页习题1.3第一题
感
谢
聆
听
~
1.4有理数的乘除法
2、如果3分钟以后记为+3分钟,那么3分钟以前应该记为 。
1、如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为 。
-2cm
-3min
教材知识点梳理
一、有理数乘法
问题铺垫
l
O
如图,有一只蜗牛沿直线 l 爬行,它现在的位置恰好在l 上的一点O。
1、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
4、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
3、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
教材知识点梳理
一、有理数乘法
O
2
4
6
8
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它在点O的 边 cm处?
每分钟2cm的速度向右记为 ; 3分钟以后记为 。
其结果可表示为 。
右
6
+2
+3
(+2)×(+3)=+6
教材知识点梳理
一、有理数乘法
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,3分钟后它在点O的 边 cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向左记为 ; 3分钟以后记为 。
其结果可表示为 。
-2
+3
(-2)×(+3)=-6
教材知识点梳理
一、有理数乘法
想一想:
问题2的结果(-2)×(+3)=-6与问题1的结果(+2)×(+3)=+6有何区别?
结论: 两个有理数相乘,改变其中一个因数的符号,积的符号也随之改变。
教材知识点梳理
一、有理数乘法
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处, 3分钟前它在点O的 边 cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向右记为 ; 3分钟以前记为 。
其结果可表示为 。
+2
-3
(+2)×(-3)=-6
教材知识点梳理
一、有理数乘法
问题一: 如果蜗牛一直以每分2cm的速度向 左爬行,现在蜗牛在点O处, 3分钟前它在点O 边 cm处?
O
2
4
6
8
右
6
每分钟2cm的速度向左记为 ; 3分钟以前记为 。
其结果可表示为 。
-2
-3
(-2)×(-3)=+6
教材知识点梳理
一、有理数乘法
想一想:
问题4的结果(-2)×(-3)=+6与问题1的结果(+2)×(+3)=+6有何区别?
结论: 两个有理数相乘,同时改变两个因数的符号,积的符号不变。
教材知识点梳理
一、有理数乘法
(+2)×(+3) = +6
(-2)×(+3)= -6
(+2)×(-3)= -6
(-2)×(-3)= +6
正数乘以正数积为 数
负数乘以正数积为 数
正数乘以负数积为 数
负数乘以负数积为 数
乘积的绝对值等于各因数绝对值的 。
规律呈现:
正
负
负
正
积
教材知识点梳理
一、有理数乘法
问题三:如果蜗牛一直以每分钟2cm的速度向右爬行,0分钟后它在什么位置?
O
2
4
6
8
问题六:如果蜗牛一直以每分钟0cm的速度向左爬行,3分钟前它在什么位置?
O
-8
-6
-4
-2
结论: 2×0= 0
结论: 0×(-3)= 0
教材知识点梳理
一、有理数乘法
乘法算式
因数特征
积的特征
(-2)×(-3)=+6
(+2)×(+3)=+6
(+2)×(-3)=-6
(-2)×(+3)=-6
(+2)×0=0
0×(-3)=0
同号
异号
一个因数为0
得正
得负
得 0
教材知识点梳理
一、有理数乘法
法则的应用:
(-5)×(-3)
(-7)×4
= +
= 15
(5 × 3)
= -
(7 × 4)
= -28
有理数相乘,先确定积的符号,再确定积的绝对值。
教材知识点梳理
一、有理数乘法
1 计算:
(1)(-3) × 9
(2)(- )×(-2)
解:
(1)(-3) × 9 = -(3 × 9 ) = -27
(2)(- )×(-2)= +( × 2 )= 1
知识点及时练
小试牛刀
(1) 6 × (- 9)
(3)(- 6)×(- 1)
(4)(- 6)× 0
(2)(- 15) ×
(5) 4 ×
(6) ×
(7)(- 12)×(- )
(8)(- 2 )×(- )
知识点及时练
结论:乘积是1的两个数互为倒数
1的倒数为
-1的倒数为
的倒数为
- 的倒数为
5的倒数为
-5的倒数为
的倒数为
- 的倒数为
1
-1
3
-3
-3
-3
教材知识点梳理
观察下列各式,它们的积是正的还是负的还是0
观察归纳
(1)2×3×4×(-5)
(2)2×3×(-4)×(-5)
(3)2×(-3)×(-4)×(-5)
(4)(-2)×(-3)×(-4)×(-5)
积是 .
积是 .
积是 .
积是 .
负
负
正
正
(5) (-3 )×0×(-4)×(-5)
积是 .
0
思考:积的正负与什么因数的个数有关
教材知识点梳理
一、有理数乘法
算一算:
(1)3×(-2)×(-4)
(2)(-2)×3×(+4)
(3)(-6)×(-5)×(-7)
(4)(-6)×0×(-8.1)×(-7.8)
=24
=-24
=-210
=0
思考:积的正负与什么因数的个数有关
教材知识点梳理
一、有理数乘法
几个不是0的数相乘,
负因数的个数是偶数时,积是正数
负因数的个数是奇数时,积是负数
并把各个因数的绝对值相乘。
认真记呦!
新知识
几个数相乘,如果其中有因数为0,那么积等于0。
教材知识点梳理
一、有理数乘法
1.填空(用>,<,= 填空)
(1)(-1)×2×(-3) 0
(2)(-7)×(-0.5)×(-3) 0
(3)(-4)×(-3)×|-2| 0
(4)5×(-6)×(-7)×0 0
>
>
<
=
知识点及时练
2.口算
(1)(-2)×3×4×(-1)
(2)(-5)×(-3)×4×(-2)
(3)(-2)×(-2)×(-2)×(-2)
(4)(-3)×(+3)×(-3)×(-3)
=24
=-120
=16
=-81
知识点及时练
3.计算
知识点及时练
解:原式=
知识点及时练
确定符号
绝对值相乘
解:原式=
确定符号
绝对值相乘
知识点及时练
第一组:
(2) (3×4)×0.25= 3×(4×0.25)=
(3) 2×(3+4)= 2×3+2×4=
(1) 2×3= 3×2=
思考:上面每小组运算分别体现了什么运算律?
2×3 3×2
(3×4)×0.25 3×(4×0.25)
2×(3+4) 2×3+2×4
6
6
3
3
14
14
=
=
=
教材知识点梳理
一、有理数乘法
5×(-4) =
15 - 35
第二组:
(2) [3×(-4)]×(- 5)=
3×[(-4)×(-5)]=
(3) 5×[3+(-7 )]=
5×3+5×(-7 ) =
(1) 5×(-6) = (-6 )×5=
-30
-30
60
60
-20
-20
5× (-6) (-6) ×5
[3×(-4)]×(- 5) 3×[(-4)×(-5)]
5×[3+(-7 )] 5×3+5×(-7 )
=
=
=
(-12)×(-5) =
3×20=
教材知识点梳理
一、有理数乘法
思考:
(1)第一组式子中数的范围是 ________;
(2)第二组式子中数的范围是 ________;
(3)比较第一组和第二组中的算式,可以发现______________________________________.
正数
有理数
各运算律在有理数范围内仍然适用
教材知识点梳理
一、有理数乘法
教材知识点梳理
一、有理数乘法
两个数相乘,交换两个因数的位置,积相等.
ab=ba
乘法交换律:
三个数相乘,先把前两个数相乘,或先把后两个数相乘,积相等.
(ab)c = a(bc)
乘法结合律:
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
乘法分配律:
a(b+c)
ab+ac
=
( + - )×12
用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=- 1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
= 3 + 2- 6
=- 1
知识点及时练
下列各式中用了哪条运算律?如何用字母表示?
(1)(-4)×8 = 8 ×(-4)
(2)[(-8)+5]+(-4)=(-8)+[5+(-4)]
(3) (-6)×[-+(- -)]=(-6)×- +(-6)×(- -)
(4)[29×(- - )] ×(-12)=29 ×[(- -)×(-12)]
(5) (-8)+(-9)=(-9)+(-8)
乘法交换律: ab=ba
分配律:a(b+c)=ab+ac
乘法结合律: (ab)c = a(bc)
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
2
3
1
2
1
2
2
3
5
6
5
6
知识点及时练
知识点及时练
① (-8)×(-12)×(-0.125)×(- )×(-0.1)
1
3
② 60×(1- - - )
1
2
1
3
1
4
③ (- )×(8-1 -4 )
3
4
1
3
④ (-11)×(- )+(-11)×2 +(-11)×(- )
2
5
3
5
1
5
① -0.4
②-5
③-2
④-22
知识点及时练
这题有错吗?错在哪里?
想一想
(-24)×( - + - )
5
8
1
6
3
4
1
3
解:
原式=
-24× -24× +24× - 24×
5
8
1
6
3
4
1
3
计算:
= - 8 -18 +4- 15
= - 41 +4
= - 37
正确解法:
特别提醒:
1.不要漏掉符号,
2.不要漏乘.
_____ ______ ______ ______
上一页
下一页
想一想
(-24)×( - + - )
5
8
1
6
3
4
1
3
计算:
= - 8 + 18 - 4 + 15
= - 12 +33
= 21
=(-24)× +(-24)×(- )+(-24)× +(-24)×(- )
1
3
3
4
1
6
5
8
知识点及时练
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期一 星期三 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
如何求这周每天上午8时的平均气温?
即 (-14)÷7
教材知识点梳理
二、有理数的除法
教材知识点梳理
二、有理数的除法
填一填
a -5 1 -1 0
a的倒数
6
1
-1
0.5
2
/
教材知识点梳理
二、有理数的除法
1、(-2) ×7=___
-14
除法是乘法的逆运算
(-14)÷7=___
-2
2、(-2)×(-4)=___
8
8÷ (-4)=___
-2
-2
-2
★
★
◆
◆
-6
-3
填空并思考:
(-3)× 2= ____
(-3)× (- 2 ) = ____
6
-2
6÷ (-3)= ___
(-6) ÷ 2= ___
你有新的发现吗?
(-6) × =
6 ×( )=
另外:
-3
-2
(-6) ÷ 2= (-6)×
6÷(-3)= 6 ×( )
教材知识点梳理
二、有理数的除法
除法可以转化为乘法
要注意两个变化!!
(1)除号变为乘号
(2)除数变为它的倒数
除以一个(不等于零)数,等于乘以这个数的倒数.
一般地,有理数的乘法与除法之间有以下关系:
教材知识点梳理
二、有理数的除法
有理数除法法则(一)
。
1)两个有理数相除,同号得_____,异号得______,并把绝对值_____。
有理数除法法则(二):
正
负
相除
0
2)0除以任何非0的数都是_____。
0 ÷5=
= 0
0 ÷(-5)=
= 0
教材知识点梳理
二、有理数的除法
法则1:除以一个不等于0的数,等于乘这个数的倒数.
法则2:两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数,都得0.
有理数的除法法则
1 计算: (1) (- 36) ÷9 ;
(2) ÷( ).
=
× ( )
=
解: (1) (-36) ÷9 = - 36 ÷9 = - 4;
(2) ( )
÷
对于这两题的计算,你有什么样的思路?
如果两数相除,能够整除就选择法则2,不能够整除就选择用法则1.
-
知识点及时练
运算中遇到小数和分数时,处理的方法与小学一样,小数化成分数,带分数化成假分数,然后相除.
2:化简下列各式:
知识点及时练
3,计算:
(1)
(2)
1除以一个不为零的数的商就是这个数的倒数.
解:
解:
知识点及时练
4.计算
(1)
解
(2)
(1)有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算
(2)乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后求出结果(乘除混合运算按从左到右的顺序进行计算)
知识点及时练
先算乘除,再算加减,同级运算从左往右依次计算,如有括号,先算括号内的.
教材知识点梳理
三、一则混合运算
混合运算的顺序
这个解法是正确的
这个解法是错误的
练习、观察下面两位的解法正确吗?若不正确,你能发现下面解法问题出在哪里吗?
知识点及时练
练习、观察下面两位同学的解法正确吗?若不正确,你能发现下面解法问题出在哪里吗?
这个解法是错误的
这个解法是正确的
还有更好的解法吗?
知识点及时练
练习、请你仔细阅读下列材料:
按常规方法计算
知识点及时练
再根据你对所提供材料的理解,选择合适的方法计算:
简便计算,先其倒数
计算(-4) ÷2,4 ÷(-2),(-4) ÷(-2).
联系这类具体的数的除法,你认为a,b是有理数,b≠0,下列式子是否成立 从它们可以总结什么规律
(1) ,(2)中的式子都成立.从它们可以总结出:分子,分母以及分数这三者的符号,改变其中的两个,分数的值不变.
(1)边长为a的正方形的面积如何表示?
(2)棱长为a的正方体的体积如何表示?
记作
记作
读作:a的平方(a的二次方)
读作:a的立方(a的三次方)
4个a相乘呢?
5个a相乘呢?
100个a相乘呢?
猜想:
问题
一般地,几个相同的因数a 相乘,即
记作: 。
读作:a的n次方
求n个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
运算
乘方
结果
幂
也可读作a的n次幂
教材知识点梳理
六、乘方
本讲之后你应该学会
1.掌握有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘
任何数与0相乘,都得0
乘积是1的两个数互为倒数
同正异负
本讲之后你应该学会
2.能用法则正确地进行有理数乘法运算
例: (1)(-3)×9;(2)8×(-1)
本讲之后你应该学会
3.能确定多个因数相乘时,积的符号,并能用法则进行多个因数的乘积运算
例:(-0.5) ×(-1) ×( - )×(-8)
本讲之后你应该学会
4.能用乘法的三个运算律来进行乘法的简化运算
乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
( + - )×12
例: 用两种方法计算
1
2
1
6
1
4
解法1:
( + - )×12
3
12
2
12
6
12
原式=
1
12
=- ×12
=- 1
解法2:
原式=
×12 + ×12- ×12
1
4
1
6
1
2
= 3 + 2- 6
=- 1
本讲之后你应该学会
本讲之后你应该学会
5.掌握有理数除法法则
除以一个不等于0的数,等于乘以这个数的倒数
两数相除,同号得正,异号得负,并把绝对值相除,0除以任何一个不等于0的数,都得0.
转化的思想
本讲之后你应该学会
6.会进行有理数的除法运算以及分数的化简
例:
本讲之后你应该学会
7.掌握有理数的加减乘除混合运算
有理数的乘方
棋盘上的学问
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“就在这个棋盘上放一些米粒吧。
退出
下一页
上一页
返回
第1格放1粒,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到第64格。”“你真傻!就要这么一点米?”,国王哈哈大笑。这位大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
退出
上一页
下一页
有一张厚度是0.1毫米的纸,将它对折50次后,请想象厚度有多高?
⑴ 对折2次后,厚度为多少毫米?
2×2×1
⑵ 对折3次后,厚度为多少毫米?
2×2×2×1
⑶ 对折4次后,厚度为多少毫米?
2×2×2×2×1
⑷ 对折50次后,厚度为多少毫米?
2×2×2×…×2×1
当要表示多个相同因数相乘时,以上写法多麻烦啊!有没有简便写法呢?
退出
上一页
下一页
小学我们学过一个数的平方和立方
2×2=
2×2×2=
则2×2×2×2=____
(-3) × (-3) × (-3) × (-3) × (-3)=
a.a.a.a.a.a.=
=
退出
上一页
下一页
个相同的因数 相乘,即
我们把它作 ;
即
这种求 个 的积的运算,叫做乘方。
乘方的结果叫做幂。
在 中, 叫做底数, 叫做指数。
幂
底数
因数
指数
因数的个数
读作 的 次方,也可以读作 的 次幂。
幂
幂
幂
幂
幂
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
指数
因数的个数
底数
因数
底数
因数
底数
因数
底数
因数
底数
因数
相同因数
相同因数
相同因数
相同因数
相同因数
退出
上一页
下一页
返回
乘方的读法
1、a的n次方
2、a的n次幂
返回
下一页
上一页
退出
练练吧一
1)在 中,12是 数,10是
数,读作 ;
表示:
2) 的底数是 ,指数是 ,读作
;
底
指
12的10次方或12的10次幂
的7次方
7
10个12 相乘
退出
上一页
下一页
返回
3、在 中,-3是 数,
16是 数,读作 ;
4、在 中,底数是 ;指数是 ;
读作 ;
底
-3的16次方
指
17
的17次方
返回
下一页
上一页
退出
(5)5看成幂的话,底数是 ,指数是 ,可读作 ;
(6) a 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
5
1
5的一次方
1
的一次方
退出
上一页
下一页
返回
练练吧二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;
退出
上一页
下一页
返回
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
下一页
上一页
退出
返回
练练吧三: 计算
(1)102 103
(2)
=100
=1000
=10000
=100
=-1000
=10000
(3)
=0.01
=0.001
=0.0001
=0.00001
(4)(-0.1) (-0.1) (-0.1) (-0.1)
=0.01
=-0.001
观察计算的结果,你发现了什么规律?
=0.0001
=-0.00001
(-10)
=-100000
10
=100000
10
规律:
(1)正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
(2)底数绝对值为10的幂的特点:1后面0的个数与指数相同。
(3)底数绝对值为0.1的幂的特点:1前面0的个数与指数相同(包括小数点前的1个零。
猜一猜
知识探索
例1、比较下列各数的值。它们一样吗?
1、 和
2、 , 和
解:1、
3、 = ;
注意到指数的位置与运算值的关系了吗?
退出
上一页
下一页
返回
2、
注意乘方中括号,负号的位置哦
思考:用乘方式子怎么表示 的相反数?
返回
下一页
上一页
退出
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
口答
1、 是 (填“正”或“负”)数;
2、 是 (填“正”或“负”)数;
3、 是 (填“正”或“负”)数;
是 (填“正”或“负”)数;
= (n不等于0);
正
负
正
1
负
退出
上一页
下一页
返回
练练吧四:
计算
(1) (2) (3)
(4) (5) (6)
(7) (8) (9)
(10)
1
1
-1
-1
0的任何次幂都得0
退出
上一页
下一页
返回
同学们,现在我们可以解决开始时的《棋盘上的学问》上的问题了吗?
退出
上一页
下一页
返回
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616
读一读
棋盘上的学问
知识梳理
1、乘方是特殊的乘法运算,所谓特殊就是所乘的因数是相同的;
2、幂是乘方运算的结果;正数的任何次幂是正数,负数的奇次幂是负数,负数 的偶次幂是正数;
3、进行乘方运算应先定符号后计算。
4、0和1的任何次幂都它本身
退出
上一页
下一页
返回
课后测验
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。
4
6
-4的7次方或-4的7次幂
负
-8
0
退出
上一页
下一页
返回
