圆与圆的位置关系[上学期]

(共18张PPT)
课件制作：林攀峰
圆和圆的位置关系
教学重点、难点
教学过程
教学重点、难点
两圆相交，相切的概念及两圆相切的性质和判定。
重点
难点
两圆的圆心距、半径与两圆位置之间的关系。
教学过程
复习提问
知识导入
例题选讲
课堂练习
小结
思维拓展
直线和圆的位置关系
d
C
d
C
d
C
l
E
F
r
r
r
直线 l与⊙A相交
d ＜r
直线 l与⊙A相切
d ＝r
直线 l与⊙A相离
d ＞r
直线 l是⊙A的割线
直线 l是⊙A的切线
两个公共点
唯一公共点
点C是切点
没有公共点
复习提问
圆和圆的五种位置关系
知识导入
相切两圆的性质
设两圆的半径为Ｒ和ｒ，圆心距为ｄ
O
A
B
P
例题选讲
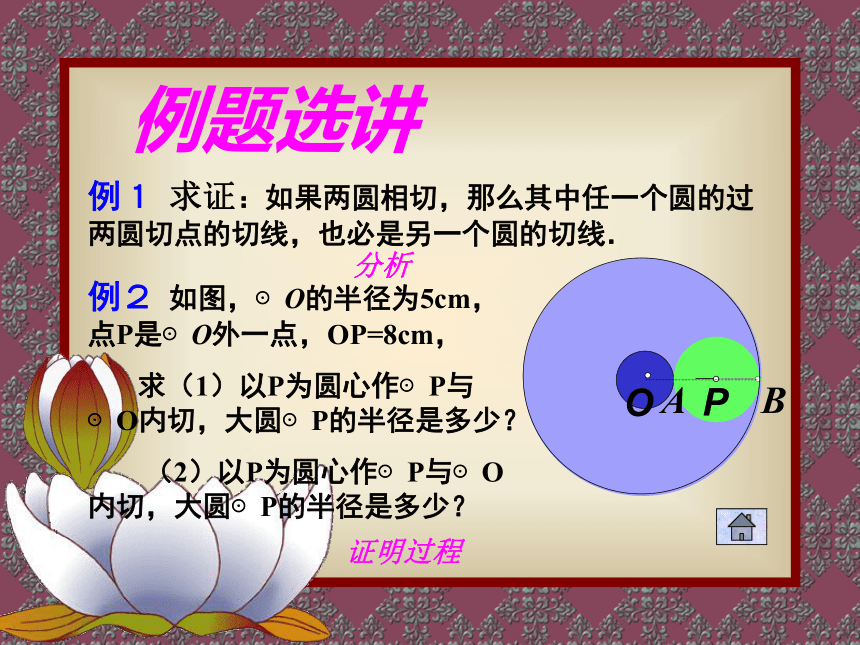
例１ 求证：如果两圆相切，那么其中任一个圆的过两圆切点的切线，也必是另一个圆的切线．
例２ 如图，⊙O的半径为5cm，点P是⊙O外一点，OP=8cm，
求（1）以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少？
（2）以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少？
证明过程
分析
例１ 求证：如果两圆相切，那么其中任一个圆的过两圆切点的切线，也必是另一个圆的切线．
分析：分两种情况讨论，
一、当两圆外切时，
二、当两圆内切时。
A
A
依据：两圆相切，连心线必过切点。
例２ 如图，⊙O的半径为5cm，点P是⊙O外一点，OP
=8cm，求（1）以P为圆心作⊙P与⊙O内切，大圆⊙P
的半径是多少？（2）以P为圆心作⊙P与⊙O内切，大圆
⊙P的半径是多少？
O
A
B
P
解: (1)设⊙O与⊙P外切于点A，则
PA=OP-OA
PA=3cm.
(2)设⊙O 与⊙P内切于点B，则
PB=OP+OB
PB=13cm.
练习
1、举出一些能表示两个圆不同位置关系的实例。
2、 ⊙O1和⊙O2的半径分别为3厘米和4厘米，设
（1） O1O2=8厘米； （2） O1O2=7厘米；
（3） O1O2=5厘米； （4） O1O2=1厘米；
（5） O1O2=0.5厘米； （6） O1和O2重合。
⊙O1和⊙O2的位置关系怎样？
3、定圆O的半径是4厘米，动圆P的半径是1厘米。
（1）设⊙P和⊙O相外切，那么点P与点O的距离
是多少？点P可以在什么样的线上移动？
（2）设⊙P和⊙O相内切，情况怎样？
如图，⊙O1与⊙O2内切于点T，⊙O1的弦TA，TB分别交⊙O2于C，D，连结AB，CD。
求证：AB∥CD
分析
证明过程
思维拓展：
分析
例２ 如图，⊙O1与⊙O2内切于点T，⊙O1的弦TA，TB分别交⊙O2于C，D，连结AB，CD。
求证：AB∥CD
问：要证AB∥CD，只要哪些角相等？
答：∠BAT=∠DCT 。
问：要证∠BAT=∠DCT ，能从图中找到合适的媒介？若不能，该怎么办？
答：添辅助线。
问：已知⊙O1与⊙O2内切，你能从例1的结果得到怎样的启发？
答：过切点T作两圆的公共切线。
证明过程
例２ 如图，⊙O1与⊙O2内切于点T，⊙O1的弦TA，TB分别交⊙O2于C，D，连结AB，CD。
求证：AB∥CD
证明：过点T作⊙O1的切线PT，则PT也是⊙O2的切线，即∠BTP既是⊙O1的弦切角，也是⊙O2的弦切角，
∴∠BAT=∠BTP，∠DCT=∠BTP,
∴∠BAT=∠DCT
∴ AB∥CD
小结
1、圆和圆的五种位置关系。
2、圆心距与半径之间的数量关系是性质定理也是判定定理。
3、相切两圆的连心线（经过两圆心的直线）必过切点。可用来证明三点共线。
4、常用的添辅助线方法：
两圆相切添两圆的公共切线
外离
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-rO1O2=R-r
0≤O1O2O1O2=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
相切两圆的性质
1、通过两圆圆心的直线叫做连心线。
2、如果两个圆相切，那么切点一定
在连心线上。
连心线：是指通过两圆圆心的一条直线。
分析：连心线是它的对称轴。两圆相切时，由
于切点是它们唯一的公共点，所以切点一定在对
称轴上。