圆与圆的位置关系[上学期]
图片预览



文档简介
课件18张PPT。
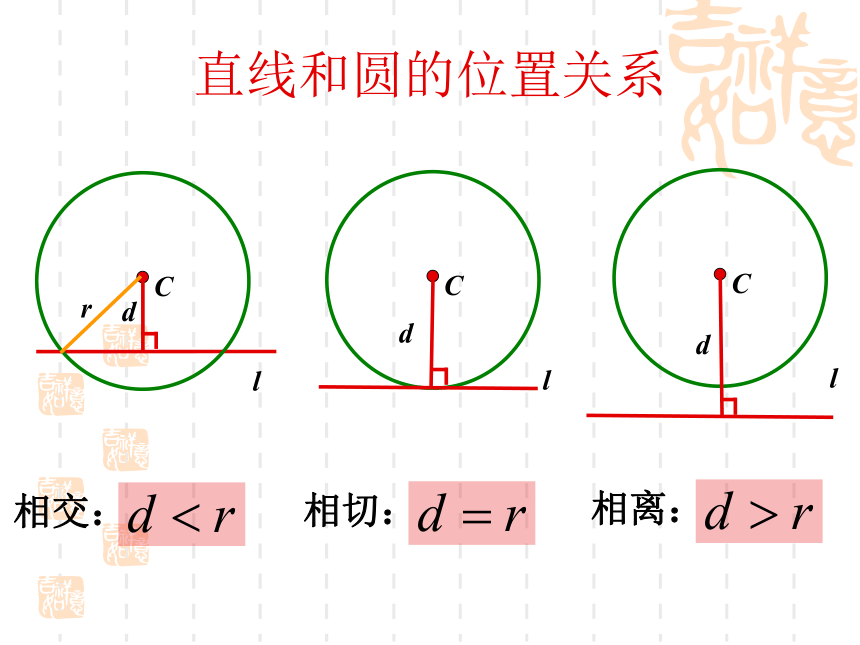
圆与圆的位置关系复习直线和圆的位置关系Cldr相交:l相切:l相离:dd练习(3分钟)1.圆心在C(0,3),经过点P(3,-1)圆的标准方程____________________。
2.圆心在C(1,3),和直线y=x相切的圆的标准方程____________________。
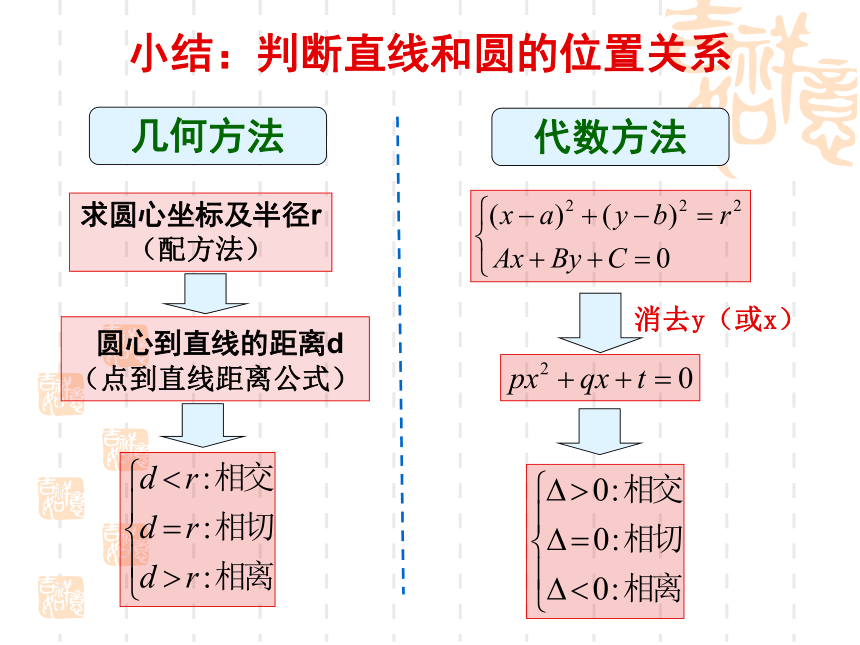
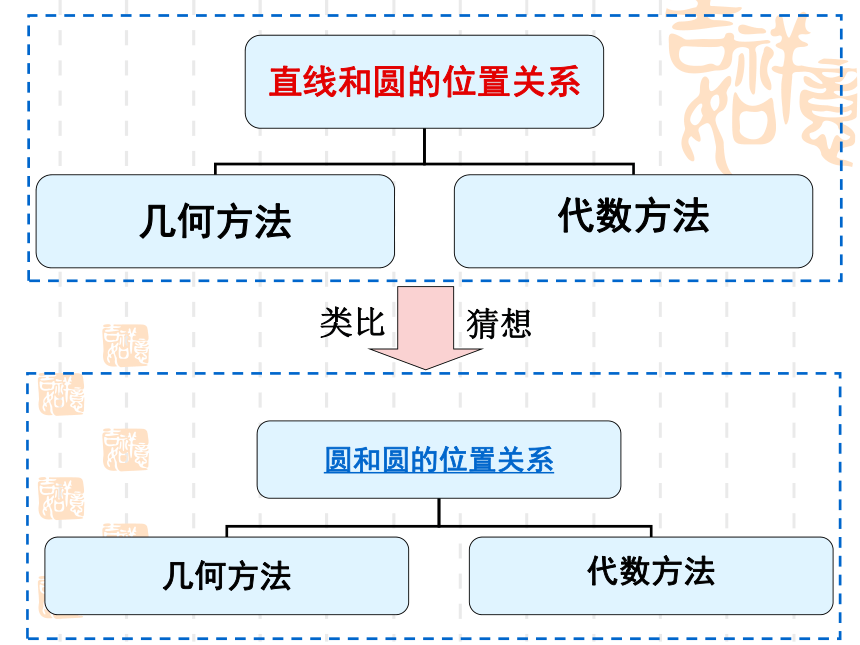
3.直线4x-3y+5=0和圆(x-1)2+(y+2)2=16的位置关系是______。相切小结:判断直线和圆的位置关系几何方法求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式)代数方法 消去y(或x)类比猜想
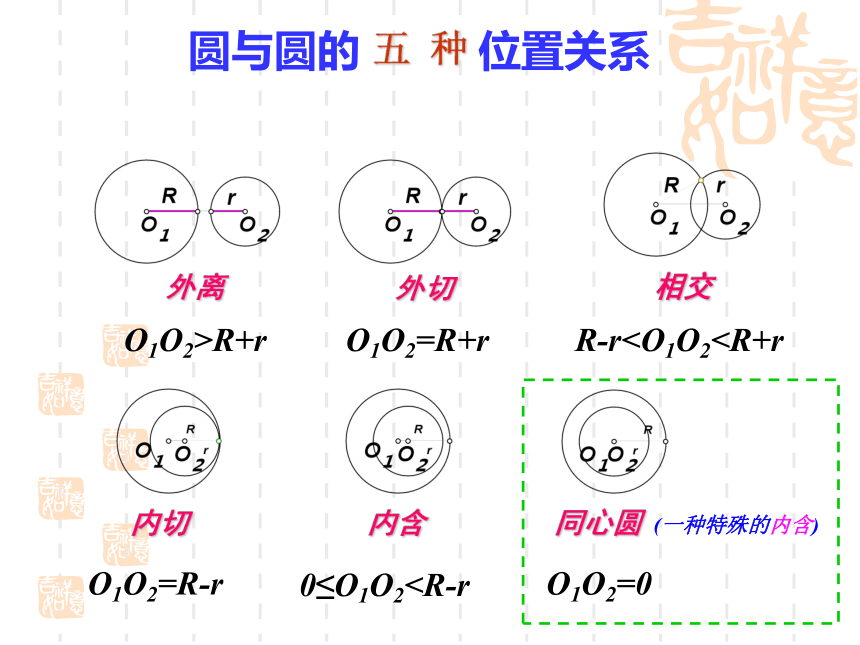
圆与圆的 位置关系外离O1O2>R+rO1O2=R+rR-r(两点间距离公式) 比较d和r1,r2的大小,下结论外离d>R+rd=R+rR-r(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法?判断C1和C2的位置关系判断C1和C2的位置关系解:联立两个方程组得①-②得把上式代入①①
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组消去二次项消元得一元二次方程用Δ判断两圆的位置关系反思判断两圆位置关系几何方法代数方法各有何优劣,如何选用?(1)当Δ=0时,有一个交点,两圆位置关系如何?内切或外切(2)当Δ<0时,没有交点,两圆位置关系如何?几何方法直观,但不能 求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判
圆的位置关系。内含或相离问题探究例1.求半径为 ,且与圆
切于原点的圆的方程。xyOCBA例2、求过两圆x2 + y2 + 6x-4= 0和x2 + y2+6y -28= 0的交点,且圆心在直线x -y - 4= 0上的圆的方程。 变题、求过两圆x2 + y2 + 6x-4= 0和x2 + y2+6y -28= 0的交点,且过(0,3)的圆的方程。 例3、一动圆与一定圆x2 + y2-6y = 0相切,且与x轴相切,求动圆圆心的轨迹方程。小结:判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)问题探究例2.求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程。yOCMNGx求圆G的圆心和半径r=|GM| 圆心是CN与MN中垂线的交点 两点式求CN方程
点(D)斜(kDG) 式求中垂线DG方程D
2.圆心在C(1,3),和直线y=x相切的圆的标准方程____________________。
3.直线4x-3y+5=0和圆(x-1)2+(y+2)2=16的位置关系是______。相切小结:判断直线和圆的位置关系几何方法求圆心坐标及半径r(配方法) 圆心到直线的距离d (点到直线距离公式)代数方法 消去y(或x)类比猜想
圆与圆的 位置关系外离O1O2>R+rO1O2=R+rR-r
②④所以方程④有两个不相等的实根x1,x2把x1,x2代入方程③得到y1,y2③所以圆C1与圆C2有两个不同的交点A(x1,y1),B(x2,y2)
联立方程组消去二次项消元得一元二次方程用Δ判断两圆的位置关系反思判断两圆位置关系几何方法代数方法各有何优劣,如何选用?(1)当Δ=0时,有一个交点,两圆位置关系如何?内切或外切(2)当Δ<0时,没有交点,两圆位置关系如何?几何方法直观,但不能 求出交点;
代数方法能求出交点,但Δ=0, Δ<0时,不能判
圆的位置关系。内含或相离问题探究例1.求半径为 ,且与圆
切于原点的圆的方程。xyOCBA例2、求过两圆x2 + y2 + 6x-4= 0和x2 + y2+6y -28= 0的交点,且圆心在直线x -y - 4= 0上的圆的方程。 变题、求过两圆x2 + y2 + 6x-4= 0和x2 + y2+6y -28= 0的交点,且过(0,3)的圆的方程。 例3、一动圆与一定圆x2 + y2-6y = 0相切,且与x轴相切,求动圆圆心的轨迹方程。小结:判断两圆位置关系几何方法两圆心坐标及半径(配方法) 圆心距d
(两点间距离公式) 比较d和r1,r2的大小,下结论代数方法 消去y(或x)问题探究例2.求经过点M(3,-1) ,且与圆
切于点N(1,2)的圆的方程。yOCMNGx求圆G的圆心和半径r=|GM| 圆心是CN与MN中垂线的交点 两点式求CN方程
点(D)斜(kDG) 式求中垂线DG方程D
