圆与圆的位置关系[上学期]

课件13张PPT。 圆和圆的位置关系复习引入1。直线和圆的位置关系有几种？直线和圆相离<=> d > r直线和圆相切<=> d = r 直线和圆相交<=> d < r1)两个圆没有公共点，并且每个圆上的点都
在另一个圆的外部时，叫做这两圆外离。2)两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部时，叫做这两个外切。这个唯一的公共点叫做切点。3)两个圆有两个公共点时，叫做这两个圆相交4)两个圆有唯一的公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部时，叫做这两个圆内切。这个唯一的公共点叫做切点。5)两个圆没有公共点，并且一个圆上的点都在另一个圆的内部时，叫做这两个圆内含。
两圆同心是两圆内含的一种特例。
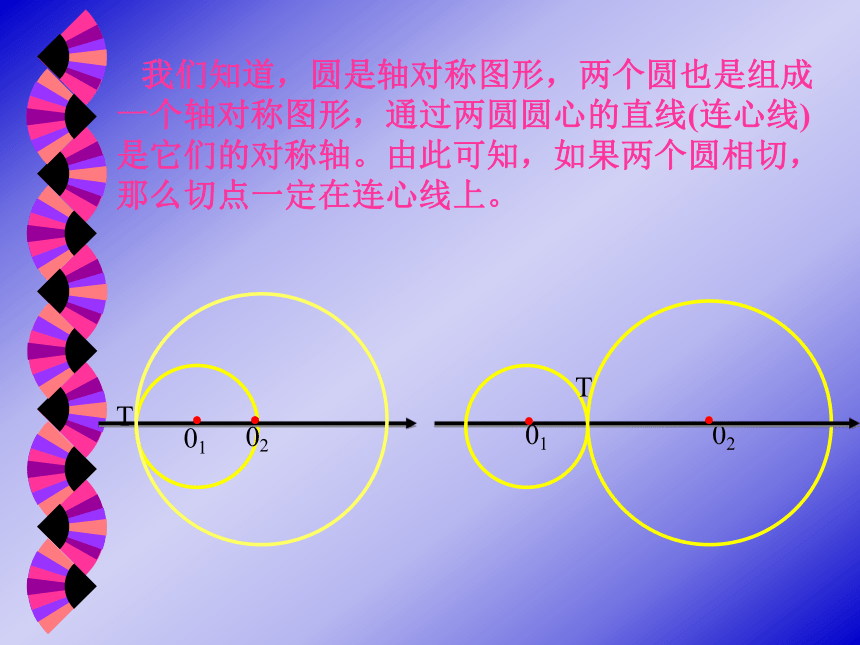
我们知道，圆是轴对称图形，两个圆也是组成 一个轴对称图形，通过两圆圆心的直线(连心线) 是它们的对称轴。由此可知，如果两个圆相切，那么切点一定在连心线上。
02T010201.T...观察图，可以发现，当两圆的半径一定时，两圆的位置关系与两圆圆心的距离的大小有关。设两圆的半径分别为R和r (R>r),圆心距为d ，那么： (5)两圆内含(4)两圆内切 (3)两圆相交 (2)两圆外切 (1)两圆外离 d>R+r d=R+r R-r求：(1)以P为圆心作⊙P与⊙O外切，小圆⊙P 的半径是多少?
(2)以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少?
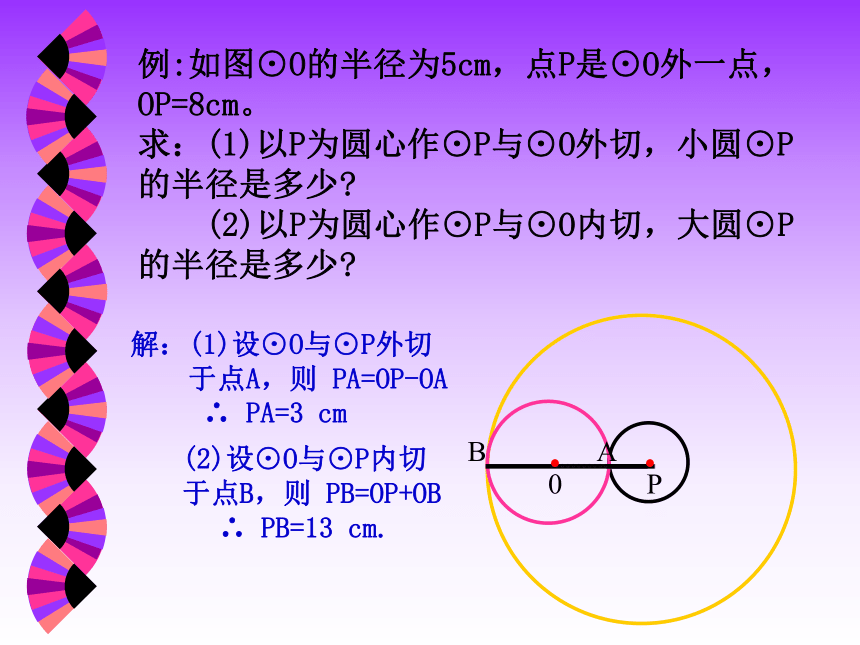
解：(1)设⊙O与⊙P外切
于点A，则 PA=OP-OA
∴ PA=3 cm(2)设⊙O与⊙P内切
于点B，则 PB=OP+OB
∴ PB=13 cm.0PAB..⊙01和⊙ 02 的半径分别为3cm 和 4 cm ,设
(1) 0102= 8cm (2) 0102 = 7cm
(3) 0102 =5cm (4) 0102 = 1cm
(5) 0102=0.5cm (6) 01和02重合
⊙0和⊙02的位置关系怎样?
练习1

(2)两圆外切 (3)两圆相交 (4)两圆内切 (5)两圆内含 (6)两圆同心答: (1)两圆相离 定圆0的半径是4cm,动圆P的半径是1cm,
(1) 设⊙ P和⊙ 0相外切,那么点P与点O的距离
是多少?点P可以在什么样的线上运动?
(2) 设⊙ P 和 ⊙O 相内切,情况又怎样?
(1) 解:∵⊙0和⊙P相外切
∴OP＝ R + r
∴OP=5cm
∴ P点在以O点为圆心,以5cm
为半径的圆上运动练习2 (2) 解: ∵⊙0和⊙P相内切
∴ OP=R-r
∴OP=3cm
∴ P点在以O点为圆心,以3cm
为半径的圆上运动两个圆的半径的比为2 : 3 ,内切时圆心距等于 8cm,那么这两圆相交时,圆心距d的取值 范围是多少? 解 设大圆半径 R = 3x,小圆半径 r = 2x
依题意得：
3x-2x=8
x=8
∴ R=24 cm r=16cm
∵ 两圆相交 R-r ∴ 8cm练习3 解 ∵两圆相交 ∴R- r △ =b2-4ac=[-2(d-R)]2-4r2
=4(d-R)2-4r2
=4(d-R+r)(d-R-r)
=4[d-(R-r)][d-(R+r)]
∵d-(R-r)>0 d-(R+r)<0
∴ 4[d-(R-r)][d-(R+r)]<0
∴ 方程没有实数根
已知⊙01和⊙02的半径分别为R和r(R>r),
圆心距为d,若两圆相交,试判定关于x的方
程x2-2(d-R)x+r2=0的根的情况。
思考题课堂小结
相离外切相交内切内含01210d>R+r
d=R+r
R-r圆的外部一圆在另一
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称布置作业课后作业