22.1.3第2课时二次函数y=a(x-h)^2的图象和性质 课件(共18张PPT)
文档属性
| 名称 | 22.1.3第2课时二次函数y=a(x-h)^2的图象和性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
22.1.3第2课时二次函数
y=a(x-h)2的图象和性质
人教版 九年级上册
教学目标
教学目标:
1.会画二次函数y=a(x-h)2的图象.
2.理解抛物线y=ax2 与抛物线 y=a(x-h)2的联系.
3.能说出抛物线y=a(x-h)2的开口方向、对称轴、顶点.
新知导入
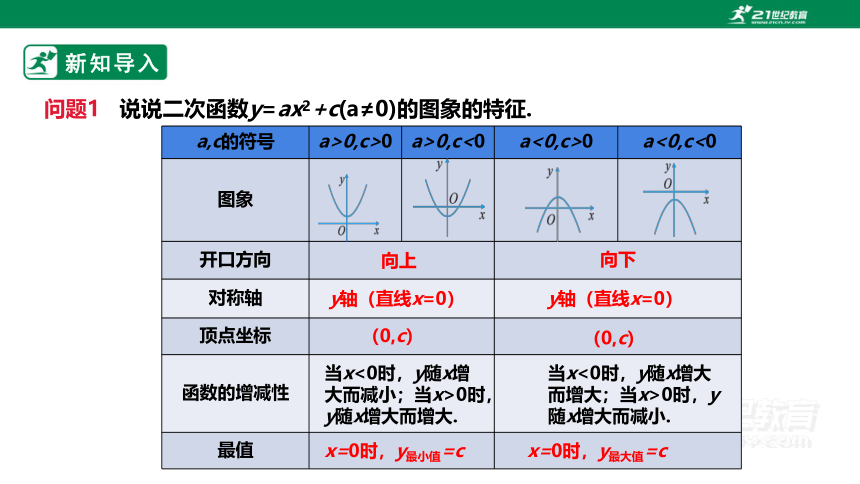
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题1 说说二次函数y=ax2+c(a≠0)的图象的特征.
新知导入
问题2 二次函数 y=ax2+k(a≠0)与 y=ax2(a ≠0) 的图象有何关系?
二次函数y=ax2+k(a ≠ 0)的图象可以由y=ax2(a ≠ 0)
的图象平移得到:
当k > 0 时,向上平移c个单位长度得到.
当k < 0 时,向下平移-c个单位长度得到.
问题3 函数 的图象,能否也可以由函数 平移得到?
新知讲解
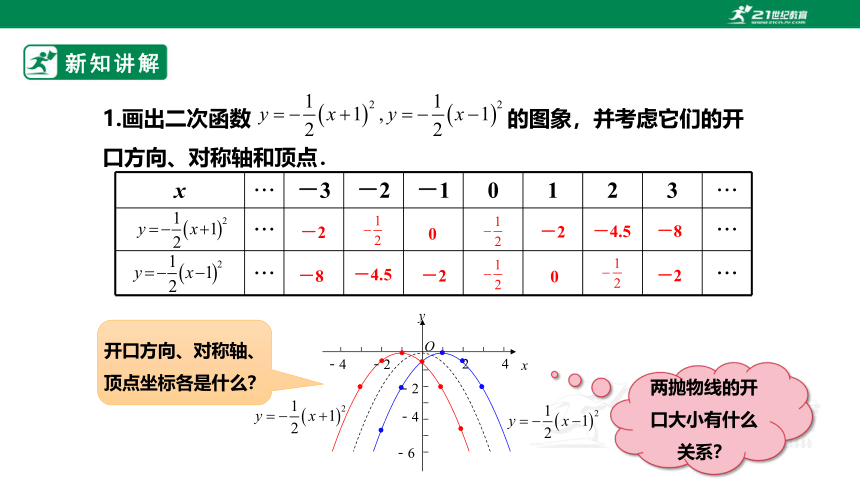
1.画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
-2
-4.5
-2
0
0
-2
-2
-4.5
-8
-2
2
-2
-4
-6
4
-4
O
x
开口方向、对称轴、顶点坐标各是什么?
两抛物线的开口大小有什么关系?
-8
y
新知讲解
x
y
O
-2
2
-2
-4
-6
4
-4
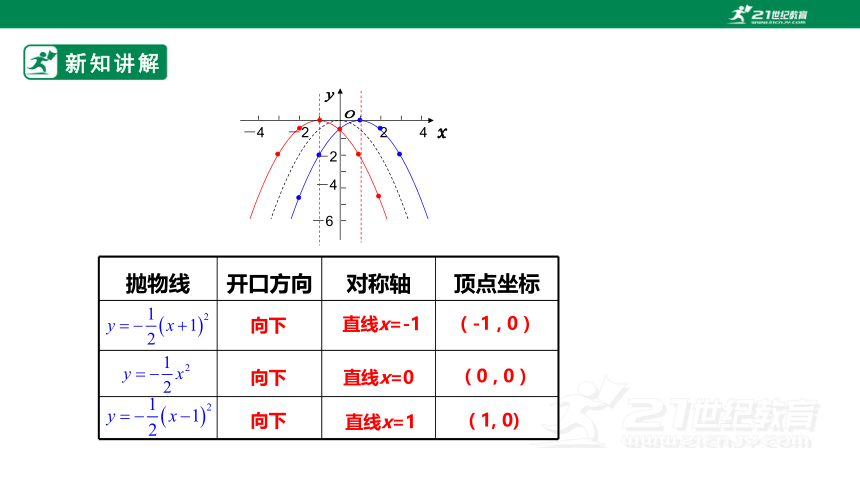
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
新知讲解
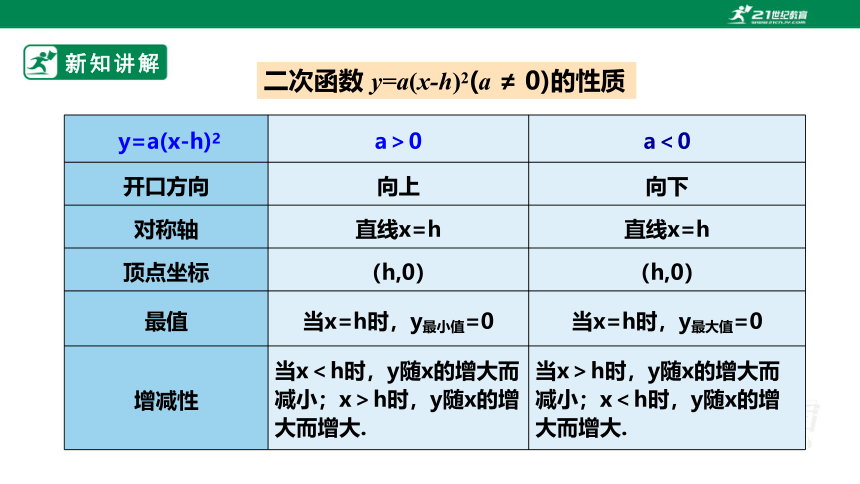
二次函数 y=a(x-h)2(a ≠ 0)的性质
y=a(x-h)2 a>0 a<0
开口方向 向上 向下
对称轴 直线x=h 直线x=h
顶点坐标 (h,0) (h,0)
最值 当x=h时,y最小值=0 当x=h时,y最大值=0
增减性 当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大. 当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
新知讲解
向右平移
1个单位
想一想
抛物线 , 与抛物线 有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
新知讲解
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到.
左右平移规律:
括号内左加右减;括号外不变.
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
巩固训练
顶点(0,0)
顶点(2,0)
直线 x=-2
直线 x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
1.在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
向右平移
2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
新知讲解
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为
y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,解得:
∴平移后二次函数关系式为y= (x-3)2.
【点睛】根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
新知讲解
例2 已知二次函数y=a(x-h)2,当x=2时有最大值,且此函数的图象经过点(1,-3),求此二次函数的解析式,并指出当x为何值时,y随x的增大而增大.
已知哪个条件可以确定h的值?
解:根据题意得y=a(x-2)2,
把(1,-3)代入得a=-3,
所以二次函数解析式为y=-3(x-2)2,
因为抛物线的对称轴为直线x=2,抛物线开口向下,
所以当x<2时,y随x的增大而增大.
课堂练习
(1)
(2)
(3)
(4)
(5)
向左平移5个单位
向右平移3个单位
?
?
向左平移2个单位
?
?
向右平移1个单位
1.请根据题意填空
向上平移2个单位
?
课堂练习
2. 把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是 .
3. 二次函数y=2(x- )2图象的对称轴是直线_______,顶点是________.
4. 若(- ,y1)(- ,y2)( ,y3)为二次函数y=(x-2)2图象上的三点,则y1 ,y2 ,y3的大小关系为_______________.
y=-(x+3)2或y=-(x-3)2
y1 >y2 > y3
课堂练习
5.已知一抛物线与抛物线y= x2+3的形状相同,开口方向相反,顶点坐标是(-5,0),根据以上特点,试写出该抛物线的解析式.
解:∵所求的抛物线与抛物线y= x2+3的形状相同,开口方向相反,
∴其二次项系数是 .
又∵顶点坐标是(-5,0),
∴所求抛物线的解析式为y= (x+5)2.
课堂练习
探索y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=h
a>0,开口向上
a<0,开口向下
y=ax2
(h,0)
性质
a>0,xx>h,y随x的增大而增大
a<0,xx>h,y随x的增大而减小
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
22.1.3第2课时二次函数
y=a(x-h)2的图象和性质
人教版 九年级上册
教学目标
教学目标:
1.会画二次函数y=a(x-h)2的图象.
2.理解抛物线y=ax2 与抛物线 y=a(x-h)2的联系.
3.能说出抛物线y=a(x-h)2的开口方向、对称轴、顶点.
新知导入
a,c的符号 a>0,c>0 a>0,c<0 a<0,c>0 a<0,c<0
图象
开口方向
对称轴
顶点坐标
函数的增减性
最值
向上
向下
y轴(直线x=0)
y轴(直线x=0)
(0,c)
(0,c)
当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
当x<0时,y随x增大而增大;当x>0时,y随x增大而减小.
x=0时,y最小值=c
x=0时,y最大值=c
问题1 说说二次函数y=ax2+c(a≠0)的图象的特征.
新知导入
问题2 二次函数 y=ax2+k(a≠0)与 y=ax2(a ≠0) 的图象有何关系?
二次函数y=ax2+k(a ≠ 0)的图象可以由y=ax2(a ≠ 0)
的图象平移得到:
当k > 0 时,向上平移c个单位长度得到.
当k < 0 时,向下平移-c个单位长度得到.
问题3 函数 的图象,能否也可以由函数 平移得到?
新知讲解
1.画出二次函数 的图象,并考虑它们的开口方向、对称轴和顶点.
x ··· -3 -2 -1 0 1 2 3 ···
··· ···
··· ···
-2
-4.5
-2
0
0
-2
-2
-4.5
-8
-2
2
-2
-4
-6
4
-4
O
x
开口方向、对称轴、顶点坐标各是什么?
两抛物线的开口大小有什么关系?
-8
y
新知讲解
x
y
O
-2
2
-2
-4
-6
4
-4
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
新知讲解
二次函数 y=a(x-h)2(a ≠ 0)的性质
y=a(x-h)2 a>0 a<0
开口方向 向上 向下
对称轴 直线x=h 直线x=h
顶点坐标 (h,0) (h,0)
最值 当x=h时,y最小值=0 当x=h时,y最大值=0
增减性 当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大. 当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
新知讲解
向右平移
1个单位
想一想
抛物线 , 与抛物线 有什么关系?
x
y
O
-2
2
-2
-4
-6
4
-4
向左平移
1个单位
新知讲解
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到.
左右平移规律:
括号内左加右减;括号外不变.
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
巩固训练
顶点(0,0)
顶点(2,0)
直线 x=-2
直线 x=2
向右平移2个单位
向左平移2个单位
顶点(-2,0)
对称轴:y轴
即直线: x=0
1.在同一坐标系中作出下列二次函数:
观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.
向右平移
2个单位
向右平移2个单位
向左平移2个单位
向左平移2个单位
新知讲解
例1 抛物线y=ax2向右平移3个单位后经过点(-1,4),求a的值和平移后的函数关系式.
解:二次函数y=ax2的图象向右平移3个单位后的二次函数关系式可表示为
y=a(x-3)2,
把x=-1,y=4代入,得4=a(-1-3)2,解得:
∴平移后二次函数关系式为y= (x-3)2.
【点睛】根据抛物线左右平移的规律,向右平移3个单位后,a不变,括号内应“减去3”;若向左平移3个单位,括号内应“加上3”,即“左加右减”.
新知讲解
例2 已知二次函数y=a(x-h)2,当x=2时有最大值,且此函数的图象经过点(1,-3),求此二次函数的解析式,并指出当x为何值时,y随x的增大而增大.
已知哪个条件可以确定h的值?
解:根据题意得y=a(x-2)2,
把(1,-3)代入得a=-3,
所以二次函数解析式为y=-3(x-2)2,
因为抛物线的对称轴为直线x=2,抛物线开口向下,
所以当x<2时,y随x的增大而增大.
课堂练习
(1)
(2)
(3)
(4)
(5)
向左平移5个单位
向右平移3个单位
?
?
向左平移2个单位
?
?
向右平移1个单位
1.请根据题意填空
向上平移2个单位
?
课堂练习
2. 把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是 .
3. 二次函数y=2(x- )2图象的对称轴是直线_______,顶点是________.
4. 若(- ,y1)(- ,y2)( ,y3)为二次函数y=(x-2)2图象上的三点,则y1 ,y2 ,y3的大小关系为_______________.
y=-(x+3)2或y=-(x-3)2
y1 >y2 > y3
课堂练习
5.已知一抛物线与抛物线y= x2+3的形状相同,开口方向相反,顶点坐标是(-5,0),根据以上特点,试写出该抛物线的解析式.
解:∵所求的抛物线与抛物线y= x2+3的形状相同,开口方向相反,
∴其二次项系数是 .
又∵顶点坐标是(-5,0),
∴所求抛物线的解析式为y= (x+5)2.
课堂练习
探索y=a(x-h)2的图象及性质
图象的画法
图象的特征
描点法
平移法
开口方向
顶点坐标
对称轴
平移关系
直线x=h
a>0,开口向上
a<0,开口向下
y=ax2
(h,0)
性质
a>0,x
a<0,x
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
