沪科版数学七年级上册 3.4.3调配问题与配套问题 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.4.3调配问题与配套问题 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-07 15:01:25 | ||
图片预览






文档简介
(共14张PPT)
3.4 二元一次方程组的应用
第3章 一次方程与方程组
第3课时 调配问题与配套问题
知识要点
1.调配问题
2.配套问题
新知导入
想一想:生活中有许多需要配套使用的物品,你能举几个例子吗?
茶壶和茶杯
课程讲授
1
调配问题
例 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
课程讲授
1
调配问题
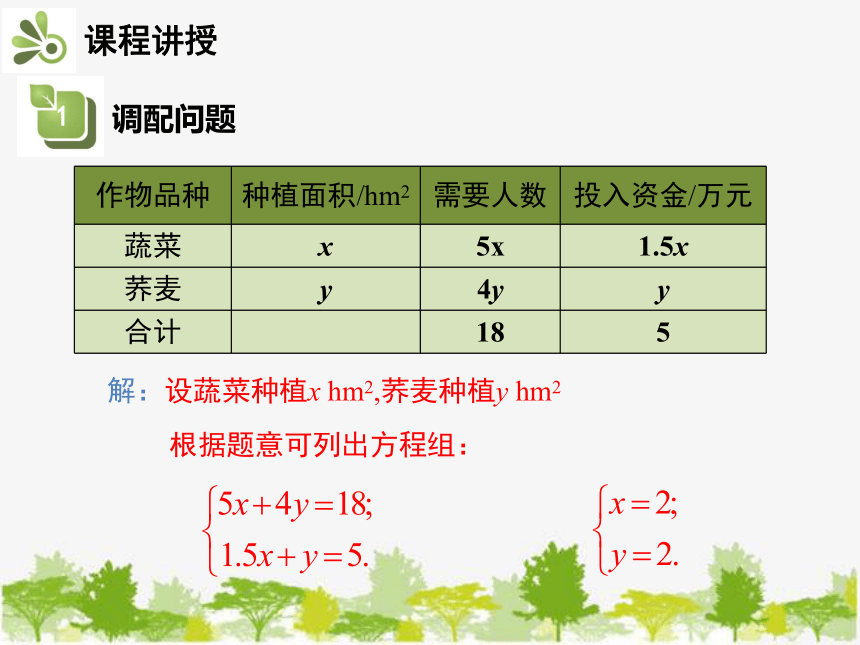
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 18 5
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
课程讲授
1
调配问题
故,承包田地的面积为: x+y=4 (hm2)
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
课程讲授
2
配套问题
例 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
课程讲授
2
配套问题
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
课程讲授
2
配套问题
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
课程讲授
2
配套问题
解决配套问题需要注意:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
随堂练习
1.某工厂第一车间人数比第二车间人数的80%还少30人,若从第二车间调10人到第一车间,那么第一车间的人数是第二车间的75%,设第一、二车间人数分别为x,y人,列出方程组为______________________.
随堂练习
2.用白铁皮做有盖的盒子,每张铁皮可生产12个盒身或18个盒盖.现有49张铁皮,怎么安排生产盒身和盒盖的铁皮张数,才使生产的盒身与盒盖配套?(一张铁皮只能生产一种产品,一个盒身配两个盒盖).设用x张铁皮生产盒身,用y张铁皮生产盒盖,可得方程组为______________________.
随堂练习
3.机械工厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮刚好配成一套,若安排x名工人加工大齿轮,安排y名工人加工小齿轮,为能使每天加工的大、小齿轮刚好配对,则所列方程组为_____________________________.
课堂小结
二元一次方程组的应用
调配问题
配套问题
3.4 二元一次方程组的应用
第3章 一次方程与方程组
第3课时 调配问题与配套问题
知识要点
1.调配问题
2.配套问题
新知导入
想一想:生活中有许多需要配套使用的物品,你能举几个例子吗?
茶壶和茶杯
课程讲授
1
调配问题
例 某村18位农民筹集5万元资金,承包了一些低产田地.根据市场调查,他们计划对种植作物的品种进行调整,该种蔬菜和荞麦.种这两种作物每公顷所需的人数和需投入的资金如下表:
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 1.5
荞麦 4 1
在现有情况下,这18位农民应承包多少公顷田地,怎样安排终止才能使所有人都有工资,且资金正好够用?
课程讲授
1
调配问题
作物品种 种植面积/hm2 需要人数 投入资金/万元
蔬菜 x 5x 1.5x
荞麦 y 4y y
合计 18 5
解:设蔬菜种植x hm2,荞麦种植y hm2
根据题意可列出方程组:
课程讲授
1
调配问题
故,承包田地的面积为: x+y=4 (hm2)
人员安排为为:
5x=5×2=10(人);4y=4×2=8(人)
答:这18位农民应承包4公顷田地,种植蔬菜和荞麦各2公顷,并安排10人种植蔬菜,8人种植荞麦,这样能使所有人都有工作且资金正好够用.
课程讲授
2
配套问题
例 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
课程讲授
2
配套问题
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
课程讲授
2
配套问题
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
答:设生产螺钉的10人,生产螺母的12人.
课程讲授
2
配套问题
解决配套问题需要注意:
(1)每套产品中各部分的比例;
(2)生产各部分的工人数之和=工人总数.
随堂练习
1.某工厂第一车间人数比第二车间人数的80%还少30人,若从第二车间调10人到第一车间,那么第一车间的人数是第二车间的75%,设第一、二车间人数分别为x,y人,列出方程组为______________________.
随堂练习
2.用白铁皮做有盖的盒子,每张铁皮可生产12个盒身或18个盒盖.现有49张铁皮,怎么安排生产盒身和盒盖的铁皮张数,才使生产的盒身与盒盖配套?(一张铁皮只能生产一种产品,一个盒身配两个盒盖).设用x张铁皮生产盒身,用y张铁皮生产盒盖,可得方程组为______________________.
随堂练习
3.机械工厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮刚好配成一套,若安排x名工人加工大齿轮,安排y名工人加工小齿轮,为能使每天加工的大、小齿轮刚好配对,则所列方程组为_____________________________.
课堂小结
二元一次方程组的应用
调配问题
配套问题
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
