第六单元可能性高频考点检测卷(单元测试) 小学数学四年级上册苏教版(含答案)
文档属性
| 名称 | 第六单元可能性高频考点检测卷(单元测试) 小学数学四年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 994.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 21:40:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六单元可能性高频考点检测卷(单元测试)-小学数学四年级上册苏教版
一、选择题
1.甲、乙两人轮流掷小正方体,约定红色面朝上算甲赢,黄色面朝上算乙赢,用下面的( )号小正方体是最公平的。
A.2红1蓝1绿2黄 B.3红2绿1黄 C.1红3蓝2黄
2.转动( )转盘,指针落在红色区域的可能性最小。
A. B. C.
3.袋子里有8个白球,8个红球,甲、乙两人先后各摸出一个球,如果同色则甲赢;如果不同色,则乙赢。在这个游戏中,( )。
A.甲赢的可能性大 B.乙赢的可能性大 C.两人赢的机会相等
4.将2个白球和9个黑球放在一个口袋里,从口袋里任意摸1个球,下列说法正确的是( )。
A.一定能摸到白球 B.一定能摸到黑球 C.摸到黑球的可能性大
5.一个正方体有六个面,有1个面上写“1”、2个面上写“2”、3个面上写“3”。抛起这个正方体,落下后数字“3”朝上的可能性( )。
A.最大
B.最小
C.与数字“2”朝上的可能性相等
D.与数字“1”朝上的可能性相等
6.奇思问爸爸的年龄,爸爸笑着说:我的年龄( )比你的年龄大。
A.不可能 B.可能 C.一定
7.袋中装有标为“1”、“2”、“3”的三个黑色球及标有“2”、“4”、“5”的三个红色球。从中任意摸一个。下列说法中正确的有( )个。
(1)摸出的一定是标有“2”的球。
(2)摸出标有“2”的球的可能性大。
(3)摸出的球共有6种可能。
(4)可能摸出红色的球。
A.2 B.3 C.4
8.下面说法正确的是( )。
A.平均数一定会和统计表中的某个数据相同。
B.条形统计图能更直观、更形象地表示数据的多少。
C.连续投掷一枚硬币20次,正面朝上的一定是10次。
二、填空题
9.口袋中有3个红球和5个黄球。
(1)从中任意摸1个球,那么摸到( )球的可能性大;
(2)如果要使摸到红球和黄球的可能性相等,要往口袋里再放( )个红球;
(3)至少一次性摸出( )个球,才能保证有一个是红球。
10.袋中有大小一样的5个白球和2个红球,任意摸一个球,可能会摸到( )球,也可能会摸到( )球,摸出( )球的可能性大。
11.一个袋子里放着同样大小的球,黑色的球有6个,白色的球有4个,从盒子里任意摸一个球,摸到( )的可能性大,至少要同时摸出( )个球,才能保证两种颜色的球都有。
12.妈妈一锅蒸了20个外形相同三种馅的饺子,其中蔬菜馅的10个,豆腐馅和肉馅的共10个,聪聪随手拿一个吃,他吃到( )馅的饺子可能性较大。
13.李老师在袋子里放了一些糖果(除颜色外其他完全相同),数量如图。从中任意摸出一颗,摸到( )色的可能性最大;摸到( )色和( )色的可能性相等。
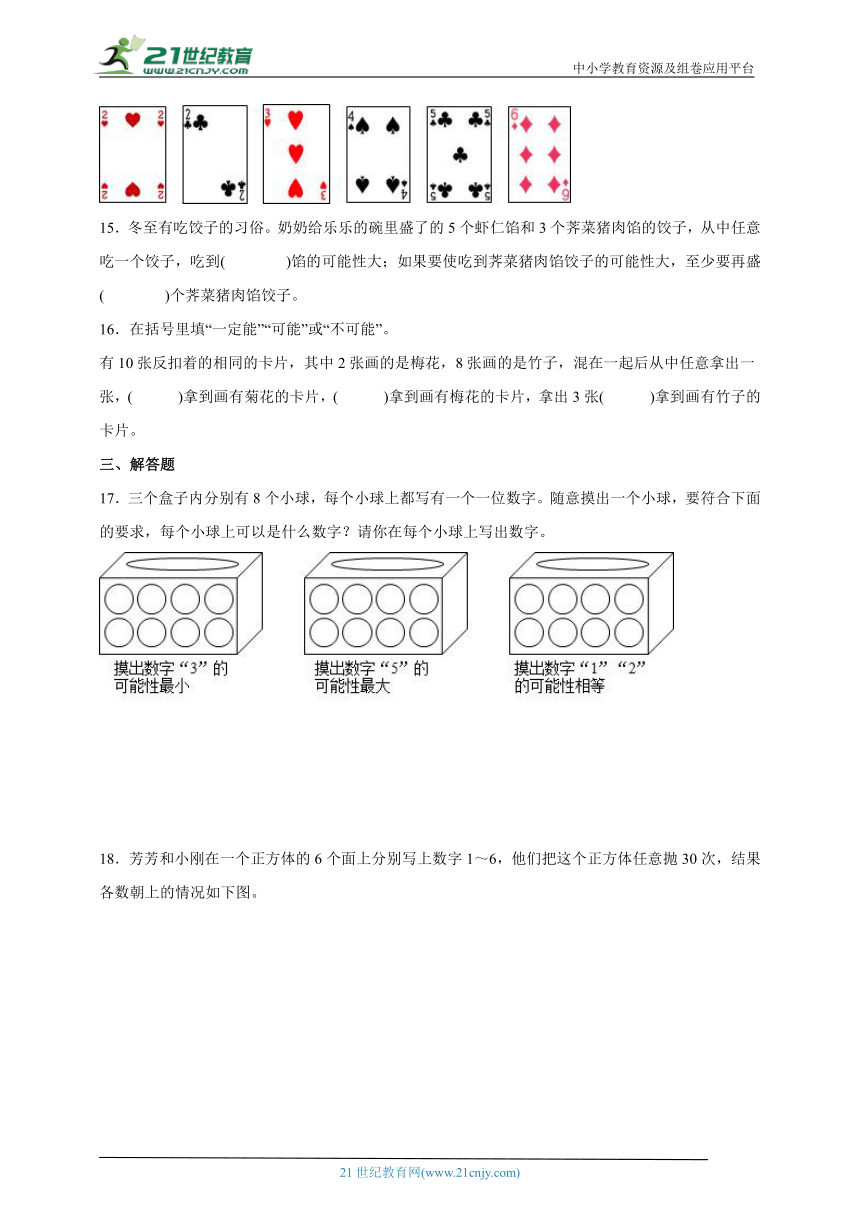
14.将下面6张扑克牌打乱顺序后反扣在桌面上,从中任意摸出一张,摸到( )的可能性比较大,摸到“ ”的可能性与与摸到“ ”的可能性( )。
15.冬至有吃饺子的习俗。奶奶给乐乐的碗里盛了的5个虾仁馅和3个荠菜猪肉馅的饺子,从中任意吃一个饺子,吃到( )馅的可能性大;如果要使吃到荠菜猪肉馅饺子的可能性大,至少要再盛( )个荠菜猪肉馅饺子。
16.在括号里填“一定能”“可能”或“不可能”。
有10张反扣着的相同的卡片,其中2张画的是梅花,8张画的是竹子,混在一起后从中任意拿出一张,( )拿到画有菊花的卡片,( )拿到画有梅花的卡片,拿出3张( )拿到画有竹子的卡片。
三、解答题
17.三个盒子内分别有8个小球,每个小球上都写有一个一位数字。随意摸出一个小球,要符合下面的要求,每个小球上可以是什么数字?请你在每个小球上写出数字。
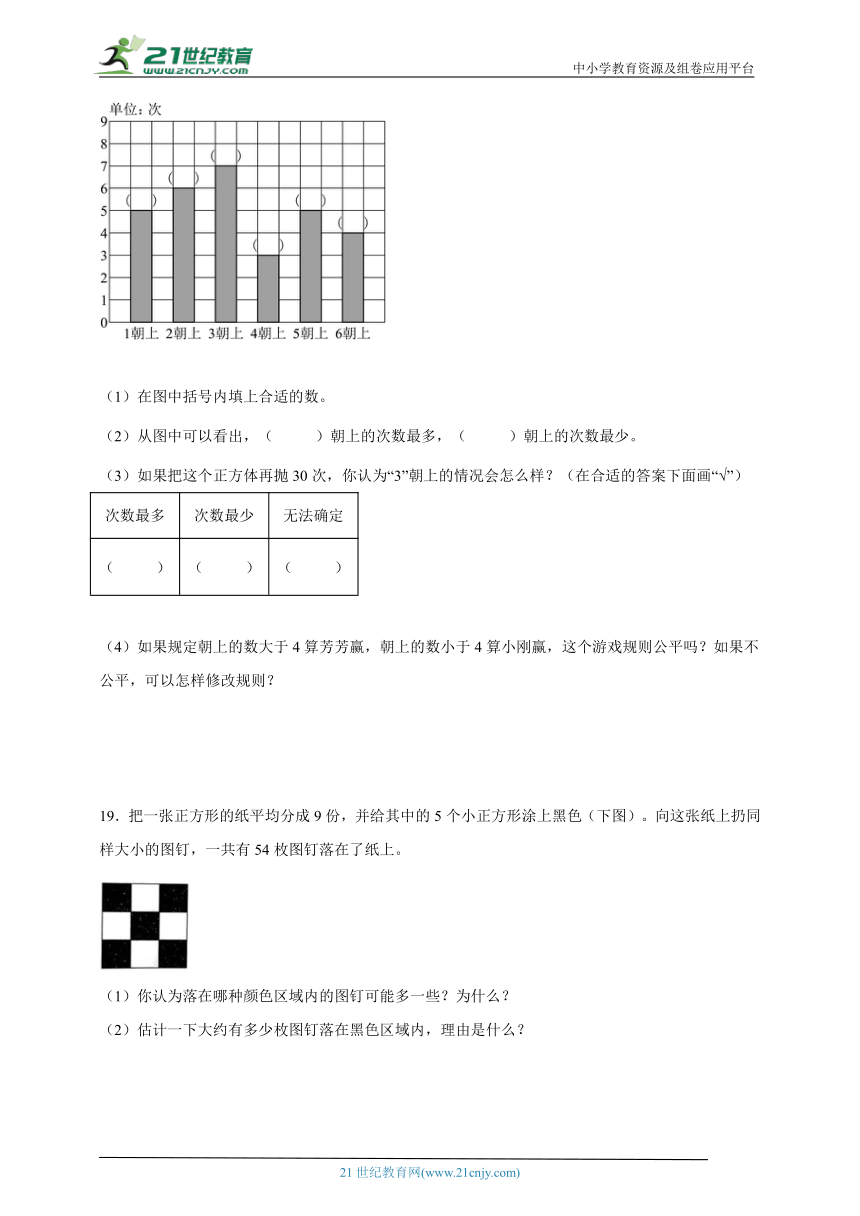
18.芳芳和小刚在一个正方体的6个面上分别写上数字1~6,他们把这个正方体任意抛30次,结果各数朝上的情况如下图。
(1)在图中括号内填上合适的数。
(2)从图中可以看出,( )朝上的次数最多,( )朝上的次数最少。
(3)如果把这个正方体再抛30次,你认为“3”朝上的情况会怎么样?(在合适的答案下面画“√”)
次数最多 次数最少 无法确定
( ) ( ) ( )
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则公平吗?如果不公平,可以怎样修改规则?
19.把一张正方形的纸平均分成9份,并给其中的5个小正方形涂上黑色(下图)。向这张纸上扔同样大小的图钉,一共有54枚图钉落在了纸上。
(1)你认为落在哪种颜色区域内的图钉可能多一些?为什么?
(2)估计一下大约有多少枚图钉落在黑色区域内,理由是什么?
20.从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,摆成末尾有0的数的可能性大还是摆成中间有0的数的可能性大?
21.幸福超市准备在2021年春节期间开展商品促销活动,每位顾客买商品满500元就可抽一次奖。在一个纸箱里任意摸一个球,摸出红球是一等奖,摸出黄球是二等奖,摸出绿球是三等奖,摸出白球不得奖。(规定纸箱里放100个球,而且四种颜色的球都要放)
(1)如果你是超市经理,准备怎样安排纸箱里的球?
(2)如果你是顾客,希望怎样安排纸箱里的球?
参考答案:
1.A
【解析】
【分析】
约定红色面朝上算甲赢,黄色面朝上算乙赢,要使得游戏公平,则红色面与黄色面的数量要一样。
【详解】
A.2红、2黄,一样多;
B.3红、1黄,不一样多;
C.1红、2黄,不一样多。
故答案为:A
【点睛】
要使游戏公平,两种的可能性得一样。
2.C
【解析】
【分析】
分析各个图形中红白黄三色区域的大小。哪种颜色的区域最小,指针落在那个区域的可能性就最小。要使指针落在红色区域的可能性最小,只需要在图形中红色区域最小即可。
【详解】
A.,红白黄三色区域同样的,指针落在三个区域的可能性同样大;
B.,红色区域最大,指针落在红色区域的可能性最大;白色区域和黄色区域一样,指针落在这两个区域的可能性相同;
C.,红色区域最小,指针落在红色区域的可能性最小。
故答案为:C
【点睛】
可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
3.B
【解析】
【分析】
甲乙两人先后各摸出一个球,即甲先摸出球后没有放回去,无论甲摸出的是什么颜色,那么乙摸的时候,有一个颜色的球的数量是7,另一个球的数量是8。根据不确定事件发生的可能性的大小与事物的数量多少有关,看甲乙两人摸出同种颜色球的可能性是不是相同的即可。
【详解】
袋子里有8个白球,8个红球,甲先摸,那么他摸出白球和红球的可能性是相同的;假设甲先摸出了一个白球,此时袋子里剩余7个白球,8个红球,那么当乙摸的时候,摸出红球的可能性大,也就是说最后不同色的可能性大,那么乙赢的可能性就大;假设甲先摸出了一个红球,此时袋子里剩余8个白球,7个红球,那么当乙摸的时候,摸出白球的可能性大,也就是说最后不同色的可能性大,那么乙赢的可能性就大。
故答案为:B
【点睛】
本题的关键是明确甲先摸出球后并没有放回袋子里,那么就导致了袋子里白球和红球的数量是不相同的,那么可能性也是不相同的。
4.C
【解析】
【分析】
根据两种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【详解】
2<9,摸到黑球的可能性大。
故答案为:C
【点睛】
不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
5.A
【解析】
【分析】
要比较可能性的大小,可以直接比较写有三个数字的面数,因为有1个面上写“1”、2个面上写“2”、3个面上写“3”,3>2>1,所以抛起这个正方体,落下后数字“3”朝上的可能性最大,据此解答。
【详解】
根据分析可知,3>2>1
所以落下后数字“3”朝上的可能性最大。
故答案为:A
【点睛】
解决此题关键是如果不需要准确地计算可能性的大小时,可以根据个数的多少,直接判断可能性的大小。
6.C
【解析】
【分析】
根据生活常识,先有爸爸,然后才有奇思,即奇思出生比爸爸晚,那么爸爸的年龄一定比奇思大。
【详解】
奇思的年龄一定比爸爸的年龄大。
故答案为:C
【点睛】
父母的年龄一定是大于孩子的年龄,根据常识解答。
7.B
【解析】
【分析】
袋子里有几种不同标号、同种标号不同颜色的球,摸出的球就有几种可能;数量多的,摸出的可能性就大。
袋子里有3个红球,3个黑球,从中任意摸出一个,可能摸到红球,也可能摸到黑球。据此解答。
【详解】
根据分析可得:
(1)袋中装有标为“1”、“2”、“3”、“4”、“5”共5个数字的球,摸出的数字有5种可能,所以摸出的一定是标有“2”的球是错误的。
(2)标为“2”的球的数量有2个,标为“1”、“3”、“4”、“5”的球的数量都是1个,所以摸出标有“2”的球的可能性大是正确的。
(3)袋中装有标为“1”、“2”、“3”的三个黑色球及标有“2”、“4”、“5”的三个红色球,共有5个数字,但是标为“2”的红色球和标为“2”的黑色球是不同的,所以摸出的球共有6种可能是正确的。
(4)袋子里有3个红球,所以可能摸出红色的球是正确的。
故答案为:B
【点睛】
不确定事件发生的可能性的大小与事物的数量多少有关。数量最多的,出现的可能性最大,数量最少的,出现的可能性最小,数量相等的,出现的可能性一样。
8.B
【解析】
【分析】
(1)平均数是全部数据的和除以数据的个数。
(2)条形统计图能很容易看出数量的多少。
(3)硬币只有正、反两面,抛出硬币,正面朝上的可能性为。
【详解】
A.如数据3,0,1,4这四个数的平均数是2,不是这组数中的某个数,所以平均数不一定是这组数据中的某一个数;故原题说法错误。
B.根据统计图的特点可知:条形统计图能直观形象地表示数量的多少;故原题说法正确。
C.一个硬币抛20次,正面朝上的可能性为,所以正面朝上的可能性是10次;故原题说法错误。
故答案为:B
【点睛】
此题涉及的知识点较多,但都比较简单,属于基础题,只要认真,容易完成,注意平时基础知识的积累。
9.(1)黄
(2)2
(3)6
【解析】
【分析】
只要总情况数不变,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相等,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
(1)
5个>3个,则从中任意摸1个球,那么摸到黄球的可能性大;
(2)
5-3=2(个),如果要使摸到红球和黄球的可能性相等,要往口袋里再放 2个红球;
(3)
5个黄球+1个红球=6个球,至少一次性摸出6个球,才能保证有一个是红球。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
10. 白 红 白
【解析】
【分析】
袋子里有红球和白球,每次任意摸一个球,可能是红球,也可能是白球;哪种颜色的球的数量多,摸到哪种颜色的球的可能性就大,反之可能性就小。
【详解】
袋中有大小一样的5个白球和2个红球,任意摸一个球,可能会摸到白球,也可能会摸到红球;5>2,摸出白球的可能性大。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
11. 黑球 7
【解析】
【分析】
黑色的球有6个,白色的球有4个,6>4,从盒子里任意摸一个球,摸到黑球的可能性大;要保证两种颜色的球都有,则要把全部黑球都摸出来,再摸1个白球即可,故6+1=7(个),据此解答。
【详解】
由分析得:
一个袋子里放着同样大小的球,黑色的球有6个,白色的球有4个,从盒子里任意摸一个球,摸到黑球的可能性大,至少要同时摸出7个球,才能保证两种颜色的球都有。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
12.蔬菜
【解析】
【分析】
根据题意,蔬菜馅的个数比较多,豆腐馅和肉馅的个数合起来才10个,数量较多的则吃到这种馅的饺子可能性较大;据此解答。
【详解】
由分析得:
蔬菜馅的个数>豆腐馅的个数
蔬菜馅的个数>肉馅的个数
则聪聪随手拿一个吃,他吃到蔬菜馅的饺子可能性较大。
【点睛】
解答此题的关键是明确数量较大的,可能性较大;数量较小的,可能性较小。
13. 红 蓝 紫
【解析】
【分析】
由题意:任意摸出一个糖果,红色糖果、黄色糖果、蓝色糖果、紫色糖果、棕色糖果都有被摸出的可能,数量多的被摸到的可能性要大,数量少的可能性就小,数量相等的摸到的可能性相等。据此解题即可。
【详解】
8>5>3>2=2
所以,李老师在袋子里放了一些糖果(除颜色外其他完全相同),数量如图。从中任意摸出一颗,摸到红色的可能性最大;摸到蓝色和紫色的可能性相等。
【点睛】
本题考查了可能性问题,5种花色的糖果,都有被模到的可有性,数量多的,摸到的可能性较大,反之,较少。
14. 2 一样大
【解析】
【分析】
根据可能性大小的知识,数量多的摸出的可能性大,反之数量少的摸出可能性小,数量相同摸到的可能性一样大,据此解答。
【详解】
看图已知,2有2张,其余数字各1张,2>1,所以从中任意选一张,摸到2的可能性比较大;“ ”和“ ”各有2张,数量一样多,所以摸到的可能性一样大。
【点睛】
本题考查可能性大小的知识运用。
15. 虾仁 3
【解析】
【分析】
5个>3个,数量较多的则吃到的可能性较大,数量较少的则吃到的可能性较小;
要使吃到荠菜猪肉馅饺子的可能性大,则荠菜猪肉馅饺子的数量大于5个,所以荠菜猪肉馅饺子的数量最少要6个,用6减3即可求出至少要再盛多少个荠菜猪肉馅饺子。
【详解】
5个>3个,则从中任意吃一个饺子,吃到虾仁馅的可能性大;
6个>5个,6-3=3(个),则要使吃到荠菜猪肉馅饺子的可能性大,至少要再盛3个荠菜猪肉馅饺子;
【点睛】
解答此题的关键是明确数量较大的,则可能性较大;数量较小的,则可能性较小。
16. 不可能 可能 一定能
【解析】
【分析】
无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】
这10张卡片里,只有竹子和梅花两种图案,其中画竹子的张数最多,有8张;画梅花的张数最少,有2张,混合后任意拿出一张:
因为没有画菊花的卡片,所以不可能拿到画有菊花的卡片。
有2张梅花卡片,所以可能拿到画有梅花的卡片。
拿出3张,因为梅花卡片只有2张,就算2张梅花卡片全部拿到了,另外一张就只能是竹子卡片,所以一定能拿到画有竹子的卡片。
【点睛】
本题的关键是明确不确定事件发生的可能性的大小与事物的数量有关。
17.③④④④⑤⑤⑥⑥;⑤⑤⑤⑤②③⑥⑦;①①①②②②⑤⑥(答案不唯一)
图见详解
【解析】
【分析】
第一种:摸出数字“3”的可能性最小,则3的数量最少即可,可以有一个小球是数字3,另外3个是数字4,2个是数字5,2个是数字6。(答案不唯一)
第二种:摸出数字“5”的可能性最大,即数字5的数量是最多的,即有4个数字5,1个数字2,一个数字3,一个数字6,一个数字7。(答案不唯一)
摸出数字“1”,“2”的可能性相等,即数字1和数字2的数量是同样多,即有3个数字1,3个数字2,1个数字5,一个数字6。(答案不唯一)
【详解】
第一个盒子:③④④④⑤⑤⑥⑥;
第二个盒子:⑤⑤⑤⑤②③⑥⑦;
第三个盒子:①①①②②②⑤⑥
图如下所示:
【点睛】
本题主要考查可能性大小,可以根据数量的多少来判断,数量越多,可能性越大。
18.(1)见详解
(2)3,4
(3)无法确定
(4)不公平,朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢
【解析】
【分析】
(1)一格代表1次,有几格代表几次。
(2)条形统计图中最长的直条表示此数朝上的次数最多,最短的直条表示此数朝上的次数最少;
(3)如果把正方体再抛30次,我认为“3”朝上的情况是无法确定,因为一个正方体上有6个数字,每抛一次,每一个数字朝上的可能性都是一样的,而且每一次的抛出都是一个独立的事件,所以无法确定“3”朝上的情况会怎么样;
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则不公平;因为大于4的数有5、6,小于4的数有1、2、3,2个<3个,所以不公平;奇数有1、3、5;偶数有2、4、6,都是3个,朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢,这时游戏规则公平。
【详解】
(1)
(2)从图中可以看出,3朝上的次数最多,4朝上的次数最少。
(3)
次数最多 次数最少 无法确定
( ) ( ) ( √ )
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则不公平;可以修改为朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢,这时游戏规则公平。
【点睛】
此题关键是根据可能性的大小进行分析、解答。
19.(1)黑色,原因见详解
(2)30枚,原因见详解
【解析】
【分析】
(1)黑色的有5块,白色的有4块,哪个颜色的多,那么哪个上面的图钉就可能多一些。
(2)黑色区域与白色区域共有9块,54除以9可以求出每块上面大概有6枚图钉,那么6乘5即可求出黑色区域上大概有几枚图钉。
【详解】
(1)5>4
答:合适区域的可能多一些,因为黑色区域的数量比白色区域的数量更多一些。
(2)54÷9×5
=6×5
=30(枚)
答:大约有30枚图钉落在黑色区域内,原因:可以根据数量求出一块上图钉大约的数量,再据此求出5块黑色区域大概能落几枚图钉。
【点睛】
哪个区域占的多,那么哪个区域的可能性就大些。
20.可能性相同
【解析】
【分析】
0、6、1、8任意取三张摆成一个三位数,一共有18种不同的情况,其中末尾有0的数有:180、810、160、610、860、680,共6个。中间有0的数有:108、801、106、601、806、608,共6个。没有0的数有:618、681、168、186、861、816,共6个。据此解答即可。
【详解】
从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,共18种情况。其中摆成末尾有0的数有6个,摆成中间有0的数有6个,二者可能性相同。
【点睛】
可能性的大小与它在总数中所占数量的多少有关。
21.见详解
【解析】
【分析】
(1)站在超市经理的立场上考虑:一等奖的数量最少,所以放的红球数量最少;二等奖的数量比一等奖稍多,所以黄球的数量要比红球的数量稍多,三等奖的数量更多一些,所以绿球的数量比黄球再多一些;不得奖的数量最多,所以白球的数量最多。
(2)站在顾客立场上考虑:一等奖的数量最多,所以放的红球数量最多;二等奖的数量比一等奖稍少,所以黄球的数量要比红球的数量稍少,三等奖的数量更少一些,所以绿球的数量比黄球再少一些;不得奖的数量最少,所以白球的数量最少。
【详解】
(1)如果我是超市经理,安排红球个数最少,黄球的数量要比红球的数量稍多,绿球的数量比黄球再多一些;白球的数量最多。
(2)如果我是顾客,放的红球数量最多;黄球的数量要比红球的数量稍少,绿球的数量比黄球再少一些;白球的数量最少。
【点睛】
可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元可能性高频考点检测卷(单元测试)-小学数学四年级上册苏教版
一、选择题
1.甲、乙两人轮流掷小正方体,约定红色面朝上算甲赢,黄色面朝上算乙赢,用下面的( )号小正方体是最公平的。
A.2红1蓝1绿2黄 B.3红2绿1黄 C.1红3蓝2黄
2.转动( )转盘,指针落在红色区域的可能性最小。
A. B. C.
3.袋子里有8个白球,8个红球,甲、乙两人先后各摸出一个球,如果同色则甲赢;如果不同色,则乙赢。在这个游戏中,( )。
A.甲赢的可能性大 B.乙赢的可能性大 C.两人赢的机会相等
4.将2个白球和9个黑球放在一个口袋里,从口袋里任意摸1个球,下列说法正确的是( )。
A.一定能摸到白球 B.一定能摸到黑球 C.摸到黑球的可能性大
5.一个正方体有六个面,有1个面上写“1”、2个面上写“2”、3个面上写“3”。抛起这个正方体,落下后数字“3”朝上的可能性( )。
A.最大
B.最小
C.与数字“2”朝上的可能性相等
D.与数字“1”朝上的可能性相等
6.奇思问爸爸的年龄,爸爸笑着说:我的年龄( )比你的年龄大。
A.不可能 B.可能 C.一定
7.袋中装有标为“1”、“2”、“3”的三个黑色球及标有“2”、“4”、“5”的三个红色球。从中任意摸一个。下列说法中正确的有( )个。
(1)摸出的一定是标有“2”的球。
(2)摸出标有“2”的球的可能性大。
(3)摸出的球共有6种可能。
(4)可能摸出红色的球。
A.2 B.3 C.4
8.下面说法正确的是( )。
A.平均数一定会和统计表中的某个数据相同。
B.条形统计图能更直观、更形象地表示数据的多少。
C.连续投掷一枚硬币20次,正面朝上的一定是10次。
二、填空题
9.口袋中有3个红球和5个黄球。
(1)从中任意摸1个球,那么摸到( )球的可能性大;
(2)如果要使摸到红球和黄球的可能性相等,要往口袋里再放( )个红球;
(3)至少一次性摸出( )个球,才能保证有一个是红球。
10.袋中有大小一样的5个白球和2个红球,任意摸一个球,可能会摸到( )球,也可能会摸到( )球,摸出( )球的可能性大。
11.一个袋子里放着同样大小的球,黑色的球有6个,白色的球有4个,从盒子里任意摸一个球,摸到( )的可能性大,至少要同时摸出( )个球,才能保证两种颜色的球都有。
12.妈妈一锅蒸了20个外形相同三种馅的饺子,其中蔬菜馅的10个,豆腐馅和肉馅的共10个,聪聪随手拿一个吃,他吃到( )馅的饺子可能性较大。
13.李老师在袋子里放了一些糖果(除颜色外其他完全相同),数量如图。从中任意摸出一颗,摸到( )色的可能性最大;摸到( )色和( )色的可能性相等。
14.将下面6张扑克牌打乱顺序后反扣在桌面上,从中任意摸出一张,摸到( )的可能性比较大,摸到“ ”的可能性与与摸到“ ”的可能性( )。
15.冬至有吃饺子的习俗。奶奶给乐乐的碗里盛了的5个虾仁馅和3个荠菜猪肉馅的饺子,从中任意吃一个饺子,吃到( )馅的可能性大;如果要使吃到荠菜猪肉馅饺子的可能性大,至少要再盛( )个荠菜猪肉馅饺子。
16.在括号里填“一定能”“可能”或“不可能”。
有10张反扣着的相同的卡片,其中2张画的是梅花,8张画的是竹子,混在一起后从中任意拿出一张,( )拿到画有菊花的卡片,( )拿到画有梅花的卡片,拿出3张( )拿到画有竹子的卡片。
三、解答题
17.三个盒子内分别有8个小球,每个小球上都写有一个一位数字。随意摸出一个小球,要符合下面的要求,每个小球上可以是什么数字?请你在每个小球上写出数字。
18.芳芳和小刚在一个正方体的6个面上分别写上数字1~6,他们把这个正方体任意抛30次,结果各数朝上的情况如下图。
(1)在图中括号内填上合适的数。
(2)从图中可以看出,( )朝上的次数最多,( )朝上的次数最少。
(3)如果把这个正方体再抛30次,你认为“3”朝上的情况会怎么样?(在合适的答案下面画“√”)
次数最多 次数最少 无法确定
( ) ( ) ( )
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则公平吗?如果不公平,可以怎样修改规则?
19.把一张正方形的纸平均分成9份,并给其中的5个小正方形涂上黑色(下图)。向这张纸上扔同样大小的图钉,一共有54枚图钉落在了纸上。
(1)你认为落在哪种颜色区域内的图钉可能多一些?为什么?
(2)估计一下大约有多少枚图钉落在黑色区域内,理由是什么?
20.从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,摆成末尾有0的数的可能性大还是摆成中间有0的数的可能性大?
21.幸福超市准备在2021年春节期间开展商品促销活动,每位顾客买商品满500元就可抽一次奖。在一个纸箱里任意摸一个球,摸出红球是一等奖,摸出黄球是二等奖,摸出绿球是三等奖,摸出白球不得奖。(规定纸箱里放100个球,而且四种颜色的球都要放)
(1)如果你是超市经理,准备怎样安排纸箱里的球?
(2)如果你是顾客,希望怎样安排纸箱里的球?
参考答案:
1.A
【解析】
【分析】
约定红色面朝上算甲赢,黄色面朝上算乙赢,要使得游戏公平,则红色面与黄色面的数量要一样。
【详解】
A.2红、2黄,一样多;
B.3红、1黄,不一样多;
C.1红、2黄,不一样多。
故答案为:A
【点睛】
要使游戏公平,两种的可能性得一样。
2.C
【解析】
【分析】
分析各个图形中红白黄三色区域的大小。哪种颜色的区域最小,指针落在那个区域的可能性就最小。要使指针落在红色区域的可能性最小,只需要在图形中红色区域最小即可。
【详解】
A.,红白黄三色区域同样的,指针落在三个区域的可能性同样大;
B.,红色区域最大,指针落在红色区域的可能性最大;白色区域和黄色区域一样,指针落在这两个区域的可能性相同;
C.,红色区域最小,指针落在红色区域的可能性最小。
故答案为:C
【点睛】
可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
3.B
【解析】
【分析】
甲乙两人先后各摸出一个球,即甲先摸出球后没有放回去,无论甲摸出的是什么颜色,那么乙摸的时候,有一个颜色的球的数量是7,另一个球的数量是8。根据不确定事件发生的可能性的大小与事物的数量多少有关,看甲乙两人摸出同种颜色球的可能性是不是相同的即可。
【详解】
袋子里有8个白球,8个红球,甲先摸,那么他摸出白球和红球的可能性是相同的;假设甲先摸出了一个白球,此时袋子里剩余7个白球,8个红球,那么当乙摸的时候,摸出红球的可能性大,也就是说最后不同色的可能性大,那么乙赢的可能性就大;假设甲先摸出了一个红球,此时袋子里剩余8个白球,7个红球,那么当乙摸的时候,摸出白球的可能性大,也就是说最后不同色的可能性大,那么乙赢的可能性就大。
故答案为:B
【点睛】
本题的关键是明确甲先摸出球后并没有放回袋子里,那么就导致了袋子里白球和红球的数量是不相同的,那么可能性也是不相同的。
4.C
【解析】
【分析】
根据两种球数量的多少,直接判断可能性的大小即可;哪种颜色的球的数量越多,摸到的可能性就越大,据此解答即可。
【详解】
2<9,摸到黑球的可能性大。
故答案为:C
【点睛】
不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小。
5.A
【解析】
【分析】
要比较可能性的大小,可以直接比较写有三个数字的面数,因为有1个面上写“1”、2个面上写“2”、3个面上写“3”,3>2>1,所以抛起这个正方体,落下后数字“3”朝上的可能性最大,据此解答。
【详解】
根据分析可知,3>2>1
所以落下后数字“3”朝上的可能性最大。
故答案为:A
【点睛】
解决此题关键是如果不需要准确地计算可能性的大小时,可以根据个数的多少,直接判断可能性的大小。
6.C
【解析】
【分析】
根据生活常识,先有爸爸,然后才有奇思,即奇思出生比爸爸晚,那么爸爸的年龄一定比奇思大。
【详解】
奇思的年龄一定比爸爸的年龄大。
故答案为:C
【点睛】
父母的年龄一定是大于孩子的年龄,根据常识解答。
7.B
【解析】
【分析】
袋子里有几种不同标号、同种标号不同颜色的球,摸出的球就有几种可能;数量多的,摸出的可能性就大。
袋子里有3个红球,3个黑球,从中任意摸出一个,可能摸到红球,也可能摸到黑球。据此解答。
【详解】
根据分析可得:
(1)袋中装有标为“1”、“2”、“3”、“4”、“5”共5个数字的球,摸出的数字有5种可能,所以摸出的一定是标有“2”的球是错误的。
(2)标为“2”的球的数量有2个,标为“1”、“3”、“4”、“5”的球的数量都是1个,所以摸出标有“2”的球的可能性大是正确的。
(3)袋中装有标为“1”、“2”、“3”的三个黑色球及标有“2”、“4”、“5”的三个红色球,共有5个数字,但是标为“2”的红色球和标为“2”的黑色球是不同的,所以摸出的球共有6种可能是正确的。
(4)袋子里有3个红球,所以可能摸出红色的球是正确的。
故答案为:B
【点睛】
不确定事件发生的可能性的大小与事物的数量多少有关。数量最多的,出现的可能性最大,数量最少的,出现的可能性最小,数量相等的,出现的可能性一样。
8.B
【解析】
【分析】
(1)平均数是全部数据的和除以数据的个数。
(2)条形统计图能很容易看出数量的多少。
(3)硬币只有正、反两面,抛出硬币,正面朝上的可能性为。
【详解】
A.如数据3,0,1,4这四个数的平均数是2,不是这组数中的某个数,所以平均数不一定是这组数据中的某一个数;故原题说法错误。
B.根据统计图的特点可知:条形统计图能直观形象地表示数量的多少;故原题说法正确。
C.一个硬币抛20次,正面朝上的可能性为,所以正面朝上的可能性是10次;故原题说法错误。
故答案为:B
【点睛】
此题涉及的知识点较多,但都比较简单,属于基础题,只要认真,容易完成,注意平时基础知识的积累。
9.(1)黄
(2)2
(3)6
【解析】
【分析】
只要总情况数不变,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相等,那么它们的可能性就相等,如果没有包含该情况就不可能发生,如果包含的全部是该情况就一定能发生。
(1)
5个>3个,则从中任意摸1个球,那么摸到黄球的可能性大;
(2)
5-3=2(个),如果要使摸到红球和黄球的可能性相等,要往口袋里再放 2个红球;
(3)
5个黄球+1个红球=6个球,至少一次性摸出6个球,才能保证有一个是红球。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
10. 白 红 白
【解析】
【分析】
袋子里有红球和白球,每次任意摸一个球,可能是红球,也可能是白球;哪种颜色的球的数量多,摸到哪种颜色的球的可能性就大,反之可能性就小。
【详解】
袋中有大小一样的5个白球和2个红球,任意摸一个球,可能会摸到白球,也可能会摸到红球;5>2,摸出白球的可能性大。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
11. 黑球 7
【解析】
【分析】
黑色的球有6个,白色的球有4个,6>4,从盒子里任意摸一个球,摸到黑球的可能性大;要保证两种颜色的球都有,则要把全部黑球都摸出来,再摸1个白球即可,故6+1=7(个),据此解答。
【详解】
由分析得:
一个袋子里放着同样大小的球,黑色的球有6个,白色的球有4个,从盒子里任意摸一个球,摸到黑球的可能性大,至少要同时摸出7个球,才能保证两种颜色的球都有。
【点睛】
本题主要考查学生对可能性的大小知识的掌握和灵活运用。
12.蔬菜
【解析】
【分析】
根据题意,蔬菜馅的个数比较多,豆腐馅和肉馅的个数合起来才10个,数量较多的则吃到这种馅的饺子可能性较大;据此解答。
【详解】
由分析得:
蔬菜馅的个数>豆腐馅的个数
蔬菜馅的个数>肉馅的个数
则聪聪随手拿一个吃,他吃到蔬菜馅的饺子可能性较大。
【点睛】
解答此题的关键是明确数量较大的,可能性较大;数量较小的,可能性较小。
13. 红 蓝 紫
【解析】
【分析】
由题意:任意摸出一个糖果,红色糖果、黄色糖果、蓝色糖果、紫色糖果、棕色糖果都有被摸出的可能,数量多的被摸到的可能性要大,数量少的可能性就小,数量相等的摸到的可能性相等。据此解题即可。
【详解】
8>5>3>2=2
所以,李老师在袋子里放了一些糖果(除颜色外其他完全相同),数量如图。从中任意摸出一颗,摸到红色的可能性最大;摸到蓝色和紫色的可能性相等。
【点睛】
本题考查了可能性问题,5种花色的糖果,都有被模到的可有性,数量多的,摸到的可能性较大,反之,较少。
14. 2 一样大
【解析】
【分析】
根据可能性大小的知识,数量多的摸出的可能性大,反之数量少的摸出可能性小,数量相同摸到的可能性一样大,据此解答。
【详解】
看图已知,2有2张,其余数字各1张,2>1,所以从中任意选一张,摸到2的可能性比较大;“ ”和“ ”各有2张,数量一样多,所以摸到的可能性一样大。
【点睛】
本题考查可能性大小的知识运用。
15. 虾仁 3
【解析】
【分析】
5个>3个,数量较多的则吃到的可能性较大,数量较少的则吃到的可能性较小;
要使吃到荠菜猪肉馅饺子的可能性大,则荠菜猪肉馅饺子的数量大于5个,所以荠菜猪肉馅饺子的数量最少要6个,用6减3即可求出至少要再盛多少个荠菜猪肉馅饺子。
【详解】
5个>3个,则从中任意吃一个饺子,吃到虾仁馅的可能性大;
6个>5个,6-3=3(个),则要使吃到荠菜猪肉馅饺子的可能性大,至少要再盛3个荠菜猪肉馅饺子;
【点睛】
解答此题的关键是明确数量较大的,则可能性较大;数量较小的,则可能性较小。
16. 不可能 可能 一定能
【解析】
【分析】
无论在什么情况下,都会发生的事件,是“一定”会发生的事件。在任何情况下,都不会发生的事件,是“不可能”事件。在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件。据此解答。
【详解】
这10张卡片里,只有竹子和梅花两种图案,其中画竹子的张数最多,有8张;画梅花的张数最少,有2张,混合后任意拿出一张:
因为没有画菊花的卡片,所以不可能拿到画有菊花的卡片。
有2张梅花卡片,所以可能拿到画有梅花的卡片。
拿出3张,因为梅花卡片只有2张,就算2张梅花卡片全部拿到了,另外一张就只能是竹子卡片,所以一定能拿到画有竹子的卡片。
【点睛】
本题的关键是明确不确定事件发生的可能性的大小与事物的数量有关。
17.③④④④⑤⑤⑥⑥;⑤⑤⑤⑤②③⑥⑦;①①①②②②⑤⑥(答案不唯一)
图见详解
【解析】
【分析】
第一种:摸出数字“3”的可能性最小,则3的数量最少即可,可以有一个小球是数字3,另外3个是数字4,2个是数字5,2个是数字6。(答案不唯一)
第二种:摸出数字“5”的可能性最大,即数字5的数量是最多的,即有4个数字5,1个数字2,一个数字3,一个数字6,一个数字7。(答案不唯一)
摸出数字“1”,“2”的可能性相等,即数字1和数字2的数量是同样多,即有3个数字1,3个数字2,1个数字5,一个数字6。(答案不唯一)
【详解】
第一个盒子:③④④④⑤⑤⑥⑥;
第二个盒子:⑤⑤⑤⑤②③⑥⑦;
第三个盒子:①①①②②②⑤⑥
图如下所示:
【点睛】
本题主要考查可能性大小,可以根据数量的多少来判断,数量越多,可能性越大。
18.(1)见详解
(2)3,4
(3)无法确定
(4)不公平,朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢
【解析】
【分析】
(1)一格代表1次,有几格代表几次。
(2)条形统计图中最长的直条表示此数朝上的次数最多,最短的直条表示此数朝上的次数最少;
(3)如果把正方体再抛30次,我认为“3”朝上的情况是无法确定,因为一个正方体上有6个数字,每抛一次,每一个数字朝上的可能性都是一样的,而且每一次的抛出都是一个独立的事件,所以无法确定“3”朝上的情况会怎么样;
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则不公平;因为大于4的数有5、6,小于4的数有1、2、3,2个<3个,所以不公平;奇数有1、3、5;偶数有2、4、6,都是3个,朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢,这时游戏规则公平。
【详解】
(1)
(2)从图中可以看出,3朝上的次数最多,4朝上的次数最少。
(3)
次数最多 次数最少 无法确定
( ) ( ) ( √ )
(4)如果规定朝上的数大于4算芳芳赢,朝上的数小于4算小刚赢,这个游戏规则不公平;可以修改为朝上的数是奇数芳芳赢,朝上的数是偶数小刚赢,这时游戏规则公平。
【点睛】
此题关键是根据可能性的大小进行分析、解答。
19.(1)黑色,原因见详解
(2)30枚,原因见详解
【解析】
【分析】
(1)黑色的有5块,白色的有4块,哪个颜色的多,那么哪个上面的图钉就可能多一些。
(2)黑色区域与白色区域共有9块,54除以9可以求出每块上面大概有6枚图钉,那么6乘5即可求出黑色区域上大概有几枚图钉。
【详解】
(1)5>4
答:合适区域的可能多一些,因为黑色区域的数量比白色区域的数量更多一些。
(2)54÷9×5
=6×5
=30(枚)
答:大约有30枚图钉落在黑色区域内,原因:可以根据数量求出一块上图钉大约的数量,再据此求出5块黑色区域大概能落几枚图钉。
【点睛】
哪个区域占的多,那么哪个区域的可能性就大些。
20.可能性相同
【解析】
【分析】
0、6、1、8任意取三张摆成一个三位数,一共有18种不同的情况,其中末尾有0的数有:180、810、160、610、860、680,共6个。中间有0的数有:108、801、106、601、806、608,共6个。没有0的数有:618、681、168、186、861、816,共6个。据此解答即可。
【详解】
从4张数字卡片 、 、 、 中任意取出3张摆成一个三位数,共18种情况。其中摆成末尾有0的数有6个,摆成中间有0的数有6个,二者可能性相同。
【点睛】
可能性的大小与它在总数中所占数量的多少有关。
21.见详解
【解析】
【分析】
(1)站在超市经理的立场上考虑:一等奖的数量最少,所以放的红球数量最少;二等奖的数量比一等奖稍多,所以黄球的数量要比红球的数量稍多,三等奖的数量更多一些,所以绿球的数量比黄球再多一些;不得奖的数量最多,所以白球的数量最多。
(2)站在顾客立场上考虑:一等奖的数量最多,所以放的红球数量最多;二等奖的数量比一等奖稍少,所以黄球的数量要比红球的数量稍少,三等奖的数量更少一些,所以绿球的数量比黄球再少一些;不得奖的数量最少,所以白球的数量最少。
【详解】
(1)如果我是超市经理,安排红球个数最少,黄球的数量要比红球的数量稍多,绿球的数量比黄球再多一些;白球的数量最多。
(2)如果我是顾客,放的红球数量最多;黄球的数量要比红球的数量稍少,绿球的数量比黄球再少一些;白球的数量最少。
【点睛】
可能性的大小与它在总数中所占数量的多少有关。在总数中占的数量越多,摸到的可能性就越大,占的数量越少,摸到的可能性就越小。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
