第六单元百分数四则混合运算经典题型练习卷(单元测试) 小学数学六年级上册苏教版(含答案)
文档属性
| 名称 | 第六单元百分数四则混合运算经典题型练习卷(单元测试) 小学数学六年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 990.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-08 22:00:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第六单元百分数四则混合运算经典题型练习卷(单元测试)-小学数学六年级上册苏教版
一、口算和估算
1.直接写出得数。
(1)7.2+3.8= (2)201-96= (3)6÷15%= (4)0.25×8=
(5)= (6)×0.4= (7)= (8)×5÷×5=
二、脱式计算
2.用递等式计算,能简算的要用简便方法计算。
0.625×(8.3-2.5×0.12)
7.6×75%+2.4÷
三、解方程或比例
3.解方程。
四、选择题
4.某种商品,先涨价10%,后来又打九折出售,这时商品的价格与原价相比( )。
A.比原价高 B.比原价低 C.与原价相同 D.无法比较
5.把25克盐溶化在100克水中,盐的重量占盐水的( )。
A.20% B.25% C.100% D.125%
6.等腰三角形的一个底角是顶角度数的50%,这个三角形是什么三角形?( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.任意三角形
7.甲、乙两堆煤,从甲堆中运给乙堆,则两堆煤相等,原来甲比乙多( )。
A.10% B.20% C.80% D.25%
8.《中华人民共和国国旗法》规定了国旗的五种通用规格,下图是宇航员杨利伟在“神舟”5号载人飞船上展示的国旗,四位同学看了这幅图,提出了自己的想法,( )想法是错误的。
甲:长是宽的 丙:长与宽的比是3∶2 乙:长比宽长 丁:宽比长短50%
A.甲 B.乙 C.丙 D.丁
9.一位集邮爱好者买了两本集邮册,每本各卖600元,一本多卖了进价的20%,另一本少卖了进价的20%,他售出这两本集邮册( )。
A.赔钱 B.赚钱 C.无法确定 D.不赔钱也不赚钱
10.本学期我市组织了小学体育学业水平监测,甲学校优秀人数占全校人数的85%,乙学校优秀人数占全校人数的85%。那么两个学校的优秀人数( )多。
A.甲学校 B.乙学校 C.一样 D.不能确定哪个学校
11.下列说法正确的是( )。
A.把一个正方体的棱长扩大2倍,则它的体积和表面积都扩大8倍。
B.0.3米∶20厘米化成最简整数比是3∶2。
C.“哥哥的身高比弟弟高”就是“弟弟的身高比哥哥矮”。
D.植树节期间,六(1)班同学植树98棵,成活98棵,成活率是98%。
五、填空题
12.0.25==3∶( )=( )%=( )折。
13.比20吨多吨是( )吨;18米比( )米多20%。
14.习总书记说:“绿水青山就是金山银山。”新华小学180名同学参加了植树节活动,其中女生人数是男生的,参加植树节的男生有( )人。据苗圃技术员介绍,同学们所栽种的这种树苗成活率一般为70%~89%,他们至少要栽( )棵树才能确保成活棵数不少于280棵。
15.中国以占世界不到10%的耕地,养活了占世界20%多的人口。这其中”杂交水稻之父”袁隆平立下了汗马功劳,他一路攻坚克难,水稻亩产量从最初的300公斤左右先后提高到500公斤、700公斤、800公斤……如今的最高纪录是1200公斤,与最初相比,如今的最高纪录整整提高了( )%。
16.2021年,第七次全国人口普查,全国共1411780000人。横线上的数改写成用“万”作单位是( )万,省略“亿”后面的尾数是( )亿。如果约70%的人接种新冠疫苗可形成群体免疫,那么至少需要( )万人接种新冠疫苗,才可能实现群体免疫。
17.用200粒种子做发芽试验,有24粒未发芽。种子的发芽率是( )。
18.王老师对本班5名参加数学竞赛的学生的成绩进行统计,以60分为标准,超过的部分用正数表示,不足的部分用负数表示。记录如下表:
20 14 ﹣2 0 5.5
这5名学生的成绩及格率是( )%,他们中成绩最高的是( )分。
19.一个商人把一件衣服标价600元,经打假人员鉴别降至60元一件出售,但仍可以赚20%,如按原价出售,则这件衣服可获暴利( )元。
六、解答题
20.修一条长1600米的水渠,已经修了全长的30%,再修多少米就修了全长的?
21.幸福饭店十二月营业额是80万。按规定,要缴纳5%的营业税,还要按营业税额的7%缴纳城市维护建设税。
(1)幸福饭店十二月应缴纳城市维护建设税多少万元?
(2)幸福饭店从十二月盈利的钱款中拿出40万元存入银行,定期五年,年利率是4.75%。到期后,应得利息多少万元?
22.张叔叔家的果园里梨树和桃树共有120棵,其中梨树的棵数是桃树的25%。桃树有多少棵?(用方程解)
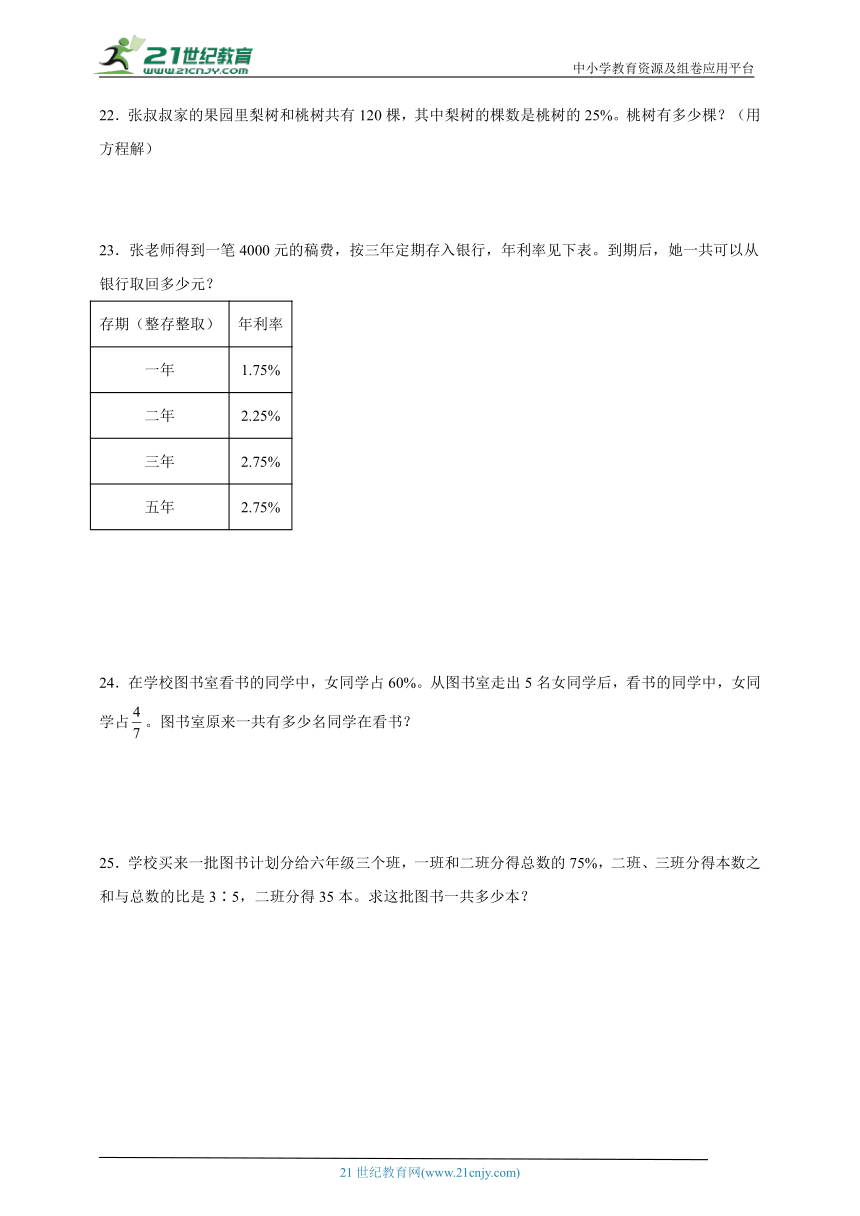
23.张老师得到一笔4000元的稿费,按三年定期存入银行,年利率见下表。到期后,她一共可以从银行取回多少元?
存期(整存整取) 年利率
一年 1.75%
二年 2.25%
三年 2.75%
五年 2.75%
24.在学校图书室看书的同学中,女同学占60%。从图书室走出5名女同学后,看书的同学中,女同学占。图书室原来一共有多少名同学在看书?
25.学校买来一批图书计划分给六年级三个班,一班和二班分得总数的75%,二班、三班分得本数之和与总数的比是3∶5,二班分得35本。求这批图书一共多少本?
参考答案:
1.(1)11;(2)105;(3)40;(4)2
(5);(6);(7);(8)25
【详解】略
2.5;3
;7.5
【分析】0.625×(8.3-2.5×0.12),先计算括号里的乘法,再计算括号里的减法,最后计算括号外的乘法;
,根据乘法分配率,原式化为:×9×12-×9×12,再进行计算;
,先计算小括号里的加法,再计算中括号里的乘法,最后计算括号外的除法。
7.6×75%+2.4÷,把除法化成乘法,原式化为:7.6×75%+2.4×,把百分数和分数化成小数,原式化为:7.6×0.75+2.4×0.75,根据乘法分配律,原式化为:0.75×(7.6+2.4),再进行计算。
【详解】0.625×(8.3-2.5×0.12)
=0.625×(8.3-0.3)
=0.625×8
=5
=×9×12-×9×12
=12-9
=3
=÷[×(+)]
=÷[×]
=÷
=×
=
7.6×75%+2.4÷
=7.6×75%+2.4×
=7.6×0.75+2.4×0.75
=0.75×(7.6+2.4)
=0.75×10
=7.5
3.x=;x=20
【分析】,先计算1-的差,再除以,即可解答;
40%x+25%x=13,先计算40%与25%的和,再用13除以40%与25%的和,即可解答。
【详解】
解:x=1-
x=
x=÷
x=×2
x=
解:65%x=13
x=13÷65%
x=20
4.B
【分析】可以假设这个商品原价是100元,先涨价10%,则此时的价格相当于原价的1+10%,单位“1”是原价,单位“1”已知,用乘法,即100×(1+10%)=110元,由于又打九折出售,此时的单位“1”是110元,单位“1”已知,用乘法,即110×90%,算出结果和原价比较即可。
【详解】假设原价是100元。
100×(1+10%)×90%
=100×110%×90%
=110×90%
=99(元)
99<100
故答案为:B。
【点睛】明确降价前后单位“1”不一致是解答本题的关键。
5.A
【分析】含盐率=盐的重量÷盐水的重量×100%,盐的重量是25克,盐水的重量是25+100=125克。据此解答。
【详解】25÷(25+100)×100%
=25÷125×100%
=20%
故答案为:A
【点睛】本题主要考查了学生对含盐率公式的掌握情况,注意要乘100%。
6.B
【分析】等腰三角形两个底角的度数相等,设顶角是x°,则一个底角是50%x°,顶角的度数+两个底角的度数=180°,据此列方程解答,求出顶角的度数再判断。
【详解】解:设顶角是x°,则一个底角是50%x°。
x+50%x×2=180
x+x=180
x=90
顶角是90°,则这个三角形是直角三角形。
故答案为:B
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
7.D
【分析】假设原来甲堆煤有10千克,运出后,运了10×=1千克,此时甲堆煤的质量:10-1=9千克,由于乙堆煤此时也是9千克,原来乙堆煤的质量:9-1=8千克,用甲比乙多的质量除以乙的质量乘100%即可求解。
【详解】假设来甲堆煤有10千克
10×=1(千克)
10-1=9(千克)
9-1=8(千克)
(10-8)÷8×100%
=2÷8×100%
=0.25×100%
=25%
故答案为:D。
【点睛】本题主要考查一个数比另一个数多百分之几,用多的量÷另一个数×100%。
8.D
【分析】甲的想法:长是宽的几分之几,用长÷宽,结果用分数表示即可;
乙的想法:长比宽长的量除以宽的长度,结果用分数表示即可;
丙的想法:根据比的意义,用长∶宽=15∶10,再根据比的基本性质化简即可;
丁的想法:用宽比长短的长度除以长的长度乘100%,把数代入即可求解,由此即可选择。
【详解】由分析可知:甲的想法:15÷10=;想法正确
乙的想法:(15-10)÷10
=5÷10
=;想法正确;
丙的想法:长∶宽=15∶10=3∶2;想法正确;
丁的想法:(15-10)÷15×100%
=5÷15×100%
≈0.333×100%
=33.3%;想法错误。
故答案为:D。
【点睛】本题主要考查百分数的应用以及比的意义,要注意一个数比另一个数多(或少)百分之几,用多的量(或少的量)÷另一个数×100%。
9.A
【分析】每本各卖600元,一本多卖了进价的20%,则这本的售价是进价的1+20%,所以这本的进价是600÷(1+20%)=500元,则此本赚了600-500=100元;另一本少卖了进价的20%,即售价是进价的1-20%,则进价是600÷(1-20%)=750元,则这本赔了750-600=150元,150>100,所以他售出这两本集邮册赔钱了。
【详解】600÷(1+20%)
=600÷1.2
=500(元)
600-500=100(元)
600÷(1-20%)
=600÷0.8
=750(元)
750-600=150(元)
150>100
故答案为:A
【点睛】首先根据进价=售价÷(1+利润率)别求出两本邮册的进价,是完成本题的关键。
10.D
【分析】甲学校优秀人数占全校人数的85%,是把甲校的全校人数看作单位“1”; 乙学校优秀人数占全校人数的85%,是把乙校的全校人数看作单位“1”。两个学校的全校人数都是未知的,则两个学校的优秀人数的多少无法确定。
【详解】本学期我市组织了小学体育学业水平监测,甲学校优秀人数占全校人数的85%,乙学校优秀人数占全校人数的85%。那么两个学校的优秀人数不能确定哪个学校多。
故答案为:D
【点睛】明确两个百分数的单位“1”不同是解题的关键。
11.B
【分析】A.可以假设正方体的棱长是1,根据正方体的表面积公式:棱长×棱长×6,体积公式:棱长×棱长×棱长,求出扩大前和扩大后的表面积以及体积,由此即可比较;
B.化成最简整数比,先把单位统一,即0.3米∶20厘米=30厘米∶20厘米,再根据比的基本性质化简即可;
C.可以假设弟弟身高是100厘米,即哥哥的身高:100×(1+)=110厘米,弟弟的身高比哥哥矮几分之几,用矮的量÷哥哥的身高,用分数表示即可;
D.根据成活率的公式:成活数量÷总数×100%,把数代入即可求解并判断。
【详解】A.假设正方体的棱长是1,扩大后的棱长:2
表面积:1×1×6
=1×6
=6;
扩大后的表面积:2×2×6
=4×6
=24;
24÷6=4,表面积扩大4倍,不符合题意;
B.0.3米∶20厘米=30厘米∶20厘米=(30÷10)∶(20÷10)=3∶2;符合题意
C.假设弟弟身高是100厘米,100×(1+)=100×=110(厘米)
(110-100)÷110
=10÷110
=;不符合题意;
D.98÷98×100%
=1×100%
=100%;不符合题意。
故答案为:B。
【点睛】本题的知识点比较多,逐个选项分析,并注意成活率的公式,如果全部成活则成活率是100%。
12.1;12;25;二五
【分析】把0.25化成分数并化简是;根据比与分数的关系,=1∶4,再根据比的基本性质比的前、后项都乘3就是3∶12;把0.25的小数点向右移动两位添上百分号就是25%;根据折扣的意义,25%就是二五折。
【详解】0.25==3∶12=25%=二五折
【点睛】此题主要是考查小数、分数、百分数、比、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
13. 20 15
【分析】比20吨多吨中的是用分数表示的数量,用加法计算。
18米比要求的未知数多20%,以这个未知的数量为单位,18相当于未知量的1+20%,用数量除以对应的分率得单位“1”量。据此解答。
【详解】20+=20(吨)
18÷(1+20%)
=18÷1.2
=15
【点睛】本题考查了对分数、百分数意义的认识。吨是物体的数量,20%是分率,再根据题目要求采用合适的计算方法,要注意区分。
14. 100 400
【分析】先把男生的人数看成单位“1”,女生人数是男生的,那么总人数就是男生人数的(1+),它对应的数量是180人,用180人除以(1+)即可求出男生的人数;
树苗成活率一般为70%~89%,要保证成活的棵数不少于280棵,那么应选择最低的成活率,把需要植树的总棵数看成单位“1”,它的70%就是280棵,根据分数除法的意义用280除以70%即可求解。
【详解】180÷(1+)
=180÷
=100(人)
280÷70%=400(棵)
【点睛】本题的关键是找出单位“1”,并找出数量对应了单位“1”的几分之几(百分之几),再用除法就可以求出单位“1”的量。
15.300%
【分析】根据题意,水稻亩产量从最初的300公斤到如今的最高纪录是1200公斤,提高了1200-300=900(公斤),然后用最初的产量÷最后的产量×100%即可得到提高率。
【详解】(1200-300)÷300×100%
=900÷300×100%
=300%
【点睛】解答此题的关键明白:提高率=提高的数量÷原来的数量×100%,据此计算即可。
16. 141178 14 98824.6
【分析】改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;
省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字;
求一个数的百分之几用乘法计算。
【详解】1411780000=141178万;
1411780000≈14亿;
141178万×70%=98824.6万
【点睛】本题主要考查整数的改写和求近似数,改写和求近似数时要注意带计数单位。
17.88%
【分析】根据题意,发芽率=发芽数量÷试验种子数量×100%,以此解答。
【详解】(200-24)÷200×100%
=176÷200×100%
=88%
【点睛】此题主要考查学生对百分率的应用。
18. 80 80
【分析】由题干可知,得到0和正数的为及格人数,再用及格人数除以总人数乘100%得及格率;用标准分60加上最大的正数就是成绩最高的分数。
【详解】由分析得,
得到0和正数的为及格有4人,及格率为:
4÷5×100%
=0.8×100%
=80%
60+20=80(分)
【点睛】此题考查的是正负数的意义,掌握正负数的意义是解题关键。
19.550
【分析】我们先求出这件衣服的进价是多少,20%的单位“1”是进价,那么60元就是进价的(1+20%),求单位“1”用除法;然后用600元减去进价就是可获的暴利。
【详解】60÷(1+20%)
=60÷120%
=50(元)
600-50=550(元)
【点睛】本题的关键是找出单位“1”是谁,找到单位“1”分析出数量关系找到分数与具体数量的对应关系问题可解。
20.720米
【分析】已经修了全长的30%,离全长的还差全长的(-30%),需要再修的长度=水渠全长×(-30%),据此解答。
【详解】1600×(-30%)
=1600×
=720(米)
答:再修720米就修了全长的。
【点睛】解答此类问题,首先找准题目中的单位“1”,表示出需要修的长度占全长的分率是解答题目的关键。
21.(1)0.28万元;(2)9.5万元
【分析】(1)十二月份的营业额是80万元,按规定要缴纳5%的营业税,把80万元看做单位“1”,要求这个饭店十二月份需缴纳营业税多少元,就是求80万元的5%是多少,用乘法先计算出营业税;按营业税的7%缴纳城市维护建设税,是把营业税总额看做单位“1”,用营业税的数额乘7%即可;
(2)由题意,本金是40万元,时间是5年,年利率是4.75%;根据关系式“利息=本金×利率×时间”即可求出利息。
【详解】(1)80×5%×7%
=4×7%
=0.28(万元)
答:幸福饭店十二月应缴纳城市维护建设税0.28万元。
(2)40×4.75%×5
=1.9×5
=9.5(万元)
答:应得利息9.5万元。
【点睛】(1)考查了关系式:营业额×税率=营业税;(2)此题重点考查了关系式“利息=本金×利率×时间”的掌握与运用。
22.96棵
【分析】设桃树有x棵,则梨树有25%x棵,根据等量关系式:桃树棵数+梨树棵数=120,列出方程求解即可。
【详解】解:设桃树有x棵,则梨树有25%x棵。
x+25%x=120
x=120
x÷=120÷
x=96
答:桃树有96棵。
【点睛】解决本题的关键在于能够根据题干找到本题的等量关系式:桃树棵数+梨树棵数=120,再据此列出方程求解。
23.4330元
【分析】根据利息=本金×利率×时间,本金4000元,三年定期利率是2.75%,时间是三年,带入数据,求出利息,再加上本金,即可解答。
【详解】4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
答:到期后,她一共可以从银行取回4330元。
【点睛】本题考查利率问题,关键熟记公式。
24.75名
【分析】设图书室原来一共有x名同学在看书,女同学占60%,女同学有60%x名。从图书馆走出5名女同学,图书馆还有x-5人,女同学占,女同学有×(x-5)人。列方程:60%x-5=×(x-5),解方程,即可解答。
【详解】解:设图书馆原来一共有x名同学在看书。
60%x-5=×(x-5)
60%x-5=x-
60%x-x=5-
x-x=
x-x=
x=
x=÷
x=×35
x=75
答:图书室原来一共有75名同学在看书。
【点睛】本题考查方程的实际应用,关键利用图书馆女同学原来的人数与走5名女同学之后的关系,列方程,解方程。
25.100本
【分析】根据题意可知,二班、三班分得本数之和与总数的比是3∶5,即二班、三班分得本数之和是总数的,设这批图书一共x本,一班、二班分得总数的75%,一班、二班分得本数是75%x本,三班分得本数用总本数-一班、二班本数和,即x-75%x;二班、三班分得本数是x-75%x+35本,二班、三班分得本数是总本数的,二班、三班分得x本,列方程:x-75%x+35=x,解方程,即可解答。
【详解】解:设这批图书一共x本。
x-75%x+35=x
0.25x+35=0.6x
0.6x-0.25x=35
0.35x=35
x=35÷0.35
x=100
答:这批图书一共100本。
【点睛】本题考查比的应用,方程的实际应用,关键明确一班、二班、三班之间的关系,利用三个班的关系,列方程,解方程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元百分数四则混合运算经典题型练习卷(单元测试)-小学数学六年级上册苏教版
一、口算和估算
1.直接写出得数。
(1)7.2+3.8= (2)201-96= (3)6÷15%= (4)0.25×8=
(5)= (6)×0.4= (7)= (8)×5÷×5=
二、脱式计算
2.用递等式计算,能简算的要用简便方法计算。
0.625×(8.3-2.5×0.12)
7.6×75%+2.4÷
三、解方程或比例
3.解方程。
四、选择题
4.某种商品,先涨价10%,后来又打九折出售,这时商品的价格与原价相比( )。
A.比原价高 B.比原价低 C.与原价相同 D.无法比较
5.把25克盐溶化在100克水中,盐的重量占盐水的( )。
A.20% B.25% C.100% D.125%
6.等腰三角形的一个底角是顶角度数的50%,这个三角形是什么三角形?( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.任意三角形
7.甲、乙两堆煤,从甲堆中运给乙堆,则两堆煤相等,原来甲比乙多( )。
A.10% B.20% C.80% D.25%
8.《中华人民共和国国旗法》规定了国旗的五种通用规格,下图是宇航员杨利伟在“神舟”5号载人飞船上展示的国旗,四位同学看了这幅图,提出了自己的想法,( )想法是错误的。
甲:长是宽的 丙:长与宽的比是3∶2 乙:长比宽长 丁:宽比长短50%
A.甲 B.乙 C.丙 D.丁
9.一位集邮爱好者买了两本集邮册,每本各卖600元,一本多卖了进价的20%,另一本少卖了进价的20%,他售出这两本集邮册( )。
A.赔钱 B.赚钱 C.无法确定 D.不赔钱也不赚钱
10.本学期我市组织了小学体育学业水平监测,甲学校优秀人数占全校人数的85%,乙学校优秀人数占全校人数的85%。那么两个学校的优秀人数( )多。
A.甲学校 B.乙学校 C.一样 D.不能确定哪个学校
11.下列说法正确的是( )。
A.把一个正方体的棱长扩大2倍,则它的体积和表面积都扩大8倍。
B.0.3米∶20厘米化成最简整数比是3∶2。
C.“哥哥的身高比弟弟高”就是“弟弟的身高比哥哥矮”。
D.植树节期间,六(1)班同学植树98棵,成活98棵,成活率是98%。
五、填空题
12.0.25==3∶( )=( )%=( )折。
13.比20吨多吨是( )吨;18米比( )米多20%。
14.习总书记说:“绿水青山就是金山银山。”新华小学180名同学参加了植树节活动,其中女生人数是男生的,参加植树节的男生有( )人。据苗圃技术员介绍,同学们所栽种的这种树苗成活率一般为70%~89%,他们至少要栽( )棵树才能确保成活棵数不少于280棵。
15.中国以占世界不到10%的耕地,养活了占世界20%多的人口。这其中”杂交水稻之父”袁隆平立下了汗马功劳,他一路攻坚克难,水稻亩产量从最初的300公斤左右先后提高到500公斤、700公斤、800公斤……如今的最高纪录是1200公斤,与最初相比,如今的最高纪录整整提高了( )%。
16.2021年,第七次全国人口普查,全国共1411780000人。横线上的数改写成用“万”作单位是( )万,省略“亿”后面的尾数是( )亿。如果约70%的人接种新冠疫苗可形成群体免疫,那么至少需要( )万人接种新冠疫苗,才可能实现群体免疫。
17.用200粒种子做发芽试验,有24粒未发芽。种子的发芽率是( )。
18.王老师对本班5名参加数学竞赛的学生的成绩进行统计,以60分为标准,超过的部分用正数表示,不足的部分用负数表示。记录如下表:
20 14 ﹣2 0 5.5
这5名学生的成绩及格率是( )%,他们中成绩最高的是( )分。
19.一个商人把一件衣服标价600元,经打假人员鉴别降至60元一件出售,但仍可以赚20%,如按原价出售,则这件衣服可获暴利( )元。
六、解答题
20.修一条长1600米的水渠,已经修了全长的30%,再修多少米就修了全长的?
21.幸福饭店十二月营业额是80万。按规定,要缴纳5%的营业税,还要按营业税额的7%缴纳城市维护建设税。
(1)幸福饭店十二月应缴纳城市维护建设税多少万元?
(2)幸福饭店从十二月盈利的钱款中拿出40万元存入银行,定期五年,年利率是4.75%。到期后,应得利息多少万元?
22.张叔叔家的果园里梨树和桃树共有120棵,其中梨树的棵数是桃树的25%。桃树有多少棵?(用方程解)
23.张老师得到一笔4000元的稿费,按三年定期存入银行,年利率见下表。到期后,她一共可以从银行取回多少元?
存期(整存整取) 年利率
一年 1.75%
二年 2.25%
三年 2.75%
五年 2.75%
24.在学校图书室看书的同学中,女同学占60%。从图书室走出5名女同学后,看书的同学中,女同学占。图书室原来一共有多少名同学在看书?
25.学校买来一批图书计划分给六年级三个班,一班和二班分得总数的75%,二班、三班分得本数之和与总数的比是3∶5,二班分得35本。求这批图书一共多少本?
参考答案:
1.(1)11;(2)105;(3)40;(4)2
(5);(6);(7);(8)25
【详解】略
2.5;3
;7.5
【分析】0.625×(8.3-2.5×0.12),先计算括号里的乘法,再计算括号里的减法,最后计算括号外的乘法;
,根据乘法分配率,原式化为:×9×12-×9×12,再进行计算;
,先计算小括号里的加法,再计算中括号里的乘法,最后计算括号外的除法。
7.6×75%+2.4÷,把除法化成乘法,原式化为:7.6×75%+2.4×,把百分数和分数化成小数,原式化为:7.6×0.75+2.4×0.75,根据乘法分配律,原式化为:0.75×(7.6+2.4),再进行计算。
【详解】0.625×(8.3-2.5×0.12)
=0.625×(8.3-0.3)
=0.625×8
=5
=×9×12-×9×12
=12-9
=3
=÷[×(+)]
=÷[×]
=÷
=×
=
7.6×75%+2.4÷
=7.6×75%+2.4×
=7.6×0.75+2.4×0.75
=0.75×(7.6+2.4)
=0.75×10
=7.5
3.x=;x=20
【分析】,先计算1-的差,再除以,即可解答;
40%x+25%x=13,先计算40%与25%的和,再用13除以40%与25%的和,即可解答。
【详解】
解:x=1-
x=
x=÷
x=×2
x=
解:65%x=13
x=13÷65%
x=20
4.B
【分析】可以假设这个商品原价是100元,先涨价10%,则此时的价格相当于原价的1+10%,单位“1”是原价,单位“1”已知,用乘法,即100×(1+10%)=110元,由于又打九折出售,此时的单位“1”是110元,单位“1”已知,用乘法,即110×90%,算出结果和原价比较即可。
【详解】假设原价是100元。
100×(1+10%)×90%
=100×110%×90%
=110×90%
=99(元)
99<100
故答案为:B。
【点睛】明确降价前后单位“1”不一致是解答本题的关键。
5.A
【分析】含盐率=盐的重量÷盐水的重量×100%,盐的重量是25克,盐水的重量是25+100=125克。据此解答。
【详解】25÷(25+100)×100%
=25÷125×100%
=20%
故答案为:A
【点睛】本题主要考查了学生对含盐率公式的掌握情况,注意要乘100%。
6.B
【分析】等腰三角形两个底角的度数相等,设顶角是x°,则一个底角是50%x°,顶角的度数+两个底角的度数=180°,据此列方程解答,求出顶角的度数再判断。
【详解】解:设顶角是x°,则一个底角是50%x°。
x+50%x×2=180
x+x=180
x=90
顶角是90°,则这个三角形是直角三角形。
故答案为:B
【点睛】列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。
7.D
【分析】假设原来甲堆煤有10千克,运出后,运了10×=1千克,此时甲堆煤的质量:10-1=9千克,由于乙堆煤此时也是9千克,原来乙堆煤的质量:9-1=8千克,用甲比乙多的质量除以乙的质量乘100%即可求解。
【详解】假设来甲堆煤有10千克
10×=1(千克)
10-1=9(千克)
9-1=8(千克)
(10-8)÷8×100%
=2÷8×100%
=0.25×100%
=25%
故答案为:D。
【点睛】本题主要考查一个数比另一个数多百分之几,用多的量÷另一个数×100%。
8.D
【分析】甲的想法:长是宽的几分之几,用长÷宽,结果用分数表示即可;
乙的想法:长比宽长的量除以宽的长度,结果用分数表示即可;
丙的想法:根据比的意义,用长∶宽=15∶10,再根据比的基本性质化简即可;
丁的想法:用宽比长短的长度除以长的长度乘100%,把数代入即可求解,由此即可选择。
【详解】由分析可知:甲的想法:15÷10=;想法正确
乙的想法:(15-10)÷10
=5÷10
=;想法正确;
丙的想法:长∶宽=15∶10=3∶2;想法正确;
丁的想法:(15-10)÷15×100%
=5÷15×100%
≈0.333×100%
=33.3%;想法错误。
故答案为:D。
【点睛】本题主要考查百分数的应用以及比的意义,要注意一个数比另一个数多(或少)百分之几,用多的量(或少的量)÷另一个数×100%。
9.A
【分析】每本各卖600元,一本多卖了进价的20%,则这本的售价是进价的1+20%,所以这本的进价是600÷(1+20%)=500元,则此本赚了600-500=100元;另一本少卖了进价的20%,即售价是进价的1-20%,则进价是600÷(1-20%)=750元,则这本赔了750-600=150元,150>100,所以他售出这两本集邮册赔钱了。
【详解】600÷(1+20%)
=600÷1.2
=500(元)
600-500=100(元)
600÷(1-20%)
=600÷0.8
=750(元)
750-600=150(元)
150>100
故答案为:A
【点睛】首先根据进价=售价÷(1+利润率)别求出两本邮册的进价,是完成本题的关键。
10.D
【分析】甲学校优秀人数占全校人数的85%,是把甲校的全校人数看作单位“1”; 乙学校优秀人数占全校人数的85%,是把乙校的全校人数看作单位“1”。两个学校的全校人数都是未知的,则两个学校的优秀人数的多少无法确定。
【详解】本学期我市组织了小学体育学业水平监测,甲学校优秀人数占全校人数的85%,乙学校优秀人数占全校人数的85%。那么两个学校的优秀人数不能确定哪个学校多。
故答案为:D
【点睛】明确两个百分数的单位“1”不同是解题的关键。
11.B
【分析】A.可以假设正方体的棱长是1,根据正方体的表面积公式:棱长×棱长×6,体积公式:棱长×棱长×棱长,求出扩大前和扩大后的表面积以及体积,由此即可比较;
B.化成最简整数比,先把单位统一,即0.3米∶20厘米=30厘米∶20厘米,再根据比的基本性质化简即可;
C.可以假设弟弟身高是100厘米,即哥哥的身高:100×(1+)=110厘米,弟弟的身高比哥哥矮几分之几,用矮的量÷哥哥的身高,用分数表示即可;
D.根据成活率的公式:成活数量÷总数×100%,把数代入即可求解并判断。
【详解】A.假设正方体的棱长是1,扩大后的棱长:2
表面积:1×1×6
=1×6
=6;
扩大后的表面积:2×2×6
=4×6
=24;
24÷6=4,表面积扩大4倍,不符合题意;
B.0.3米∶20厘米=30厘米∶20厘米=(30÷10)∶(20÷10)=3∶2;符合题意
C.假设弟弟身高是100厘米,100×(1+)=100×=110(厘米)
(110-100)÷110
=10÷110
=;不符合题意;
D.98÷98×100%
=1×100%
=100%;不符合题意。
故答案为:B。
【点睛】本题的知识点比较多,逐个选项分析,并注意成活率的公式,如果全部成活则成活率是100%。
12.1;12;25;二五
【分析】把0.25化成分数并化简是;根据比与分数的关系,=1∶4,再根据比的基本性质比的前、后项都乘3就是3∶12;把0.25的小数点向右移动两位添上百分号就是25%;根据折扣的意义,25%就是二五折。
【详解】0.25==3∶12=25%=二五折
【点睛】此题主要是考查小数、分数、百分数、比、折扣之间的关系及转化。利用它们之间的关系和性质进行转化即可。
13. 20 15
【分析】比20吨多吨中的是用分数表示的数量,用加法计算。
18米比要求的未知数多20%,以这个未知的数量为单位,18相当于未知量的1+20%,用数量除以对应的分率得单位“1”量。据此解答。
【详解】20+=20(吨)
18÷(1+20%)
=18÷1.2
=15
【点睛】本题考查了对分数、百分数意义的认识。吨是物体的数量,20%是分率,再根据题目要求采用合适的计算方法,要注意区分。
14. 100 400
【分析】先把男生的人数看成单位“1”,女生人数是男生的,那么总人数就是男生人数的(1+),它对应的数量是180人,用180人除以(1+)即可求出男生的人数;
树苗成活率一般为70%~89%,要保证成活的棵数不少于280棵,那么应选择最低的成活率,把需要植树的总棵数看成单位“1”,它的70%就是280棵,根据分数除法的意义用280除以70%即可求解。
【详解】180÷(1+)
=180÷
=100(人)
280÷70%=400(棵)
【点睛】本题的关键是找出单位“1”,并找出数量对应了单位“1”的几分之几(百分之几),再用除法就可以求出单位“1”的量。
15.300%
【分析】根据题意,水稻亩产量从最初的300公斤到如今的最高纪录是1200公斤,提高了1200-300=900(公斤),然后用最初的产量÷最后的产量×100%即可得到提高率。
【详解】(1200-300)÷300×100%
=900÷300×100%
=300%
【点睛】解答此题的关键明白:提高率=提高的数量÷原来的数量×100%,据此计算即可。
16. 141178 14 98824.6
【分析】改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;
省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字;
求一个数的百分之几用乘法计算。
【详解】1411780000=141178万;
1411780000≈14亿;
141178万×70%=98824.6万
【点睛】本题主要考查整数的改写和求近似数,改写和求近似数时要注意带计数单位。
17.88%
【分析】根据题意,发芽率=发芽数量÷试验种子数量×100%,以此解答。
【详解】(200-24)÷200×100%
=176÷200×100%
=88%
【点睛】此题主要考查学生对百分率的应用。
18. 80 80
【分析】由题干可知,得到0和正数的为及格人数,再用及格人数除以总人数乘100%得及格率;用标准分60加上最大的正数就是成绩最高的分数。
【详解】由分析得,
得到0和正数的为及格有4人,及格率为:
4÷5×100%
=0.8×100%
=80%
60+20=80(分)
【点睛】此题考查的是正负数的意义,掌握正负数的意义是解题关键。
19.550
【分析】我们先求出这件衣服的进价是多少,20%的单位“1”是进价,那么60元就是进价的(1+20%),求单位“1”用除法;然后用600元减去进价就是可获的暴利。
【详解】60÷(1+20%)
=60÷120%
=50(元)
600-50=550(元)
【点睛】本题的关键是找出单位“1”是谁,找到单位“1”分析出数量关系找到分数与具体数量的对应关系问题可解。
20.720米
【分析】已经修了全长的30%,离全长的还差全长的(-30%),需要再修的长度=水渠全长×(-30%),据此解答。
【详解】1600×(-30%)
=1600×
=720(米)
答:再修720米就修了全长的。
【点睛】解答此类问题,首先找准题目中的单位“1”,表示出需要修的长度占全长的分率是解答题目的关键。
21.(1)0.28万元;(2)9.5万元
【分析】(1)十二月份的营业额是80万元,按规定要缴纳5%的营业税,把80万元看做单位“1”,要求这个饭店十二月份需缴纳营业税多少元,就是求80万元的5%是多少,用乘法先计算出营业税;按营业税的7%缴纳城市维护建设税,是把营业税总额看做单位“1”,用营业税的数额乘7%即可;
(2)由题意,本金是40万元,时间是5年,年利率是4.75%;根据关系式“利息=本金×利率×时间”即可求出利息。
【详解】(1)80×5%×7%
=4×7%
=0.28(万元)
答:幸福饭店十二月应缴纳城市维护建设税0.28万元。
(2)40×4.75%×5
=1.9×5
=9.5(万元)
答:应得利息9.5万元。
【点睛】(1)考查了关系式:营业额×税率=营业税;(2)此题重点考查了关系式“利息=本金×利率×时间”的掌握与运用。
22.96棵
【分析】设桃树有x棵,则梨树有25%x棵,根据等量关系式:桃树棵数+梨树棵数=120,列出方程求解即可。
【详解】解:设桃树有x棵,则梨树有25%x棵。
x+25%x=120
x=120
x÷=120÷
x=96
答:桃树有96棵。
【点睛】解决本题的关键在于能够根据题干找到本题的等量关系式:桃树棵数+梨树棵数=120,再据此列出方程求解。
23.4330元
【分析】根据利息=本金×利率×时间,本金4000元,三年定期利率是2.75%,时间是三年,带入数据,求出利息,再加上本金,即可解答。
【详解】4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
答:到期后,她一共可以从银行取回4330元。
【点睛】本题考查利率问题,关键熟记公式。
24.75名
【分析】设图书室原来一共有x名同学在看书,女同学占60%,女同学有60%x名。从图书馆走出5名女同学,图书馆还有x-5人,女同学占,女同学有×(x-5)人。列方程:60%x-5=×(x-5),解方程,即可解答。
【详解】解:设图书馆原来一共有x名同学在看书。
60%x-5=×(x-5)
60%x-5=x-
60%x-x=5-
x-x=
x-x=
x=
x=÷
x=×35
x=75
答:图书室原来一共有75名同学在看书。
【点睛】本题考查方程的实际应用,关键利用图书馆女同学原来的人数与走5名女同学之后的关系,列方程,解方程。
25.100本
【分析】根据题意可知,二班、三班分得本数之和与总数的比是3∶5,即二班、三班分得本数之和是总数的,设这批图书一共x本,一班、二班分得总数的75%,一班、二班分得本数是75%x本,三班分得本数用总本数-一班、二班本数和,即x-75%x;二班、三班分得本数是x-75%x+35本,二班、三班分得本数是总本数的,二班、三班分得x本,列方程:x-75%x+35=x,解方程,即可解答。
【详解】解:设这批图书一共x本。
x-75%x+35=x
0.25x+35=0.6x
0.6x-0.25x=35
0.35x=35
x=35÷0.35
x=100
答:这批图书一共100本。
【点睛】本题考查比的应用,方程的实际应用,关键明确一班、二班、三班之间的关系,利用三个班的关系,列方程,解方程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
