(2022秋新教材)第八单元数学广角——数与形高频考点检测卷(单元测试) 小学数学六年级上册人教版(含答案)
文档属性
| 名称 | (2022秋新教材)第八单元数学广角——数与形高频考点检测卷(单元测试) 小学数学六年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1009.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 15:07:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八单元数与形高频考点检测卷(单元测试)-小学数学六年级上册人教版
一、选择题
1.如图,用同样的小棒去摆,第n个图形需要小棒的根数表示错误的式子是( )。
A.4n-1 B.4+ 3(n-1) C.3n+1
2.如图,用同样的小棒去摆,第n个图形需要小棒的根数是( )。
A.3n B.2n+1 C.3n-1
3.第四幅图形最外圈(阴影部分)有( )个“●”。
A.36 B.25 C.20
4.摆一个正方形需要4根小棒,以后每加一个正方形需要加3根小棒,按此方法,摆10个正方形共需( )根小棒。
A.27 B.30 C.40 D.31
5.观察下列图形,则第n个图形中三角形的个数是( )。
A. B. C. D.
6.仔细分析,第7个图形一共有( )个小三角形。
A.25 B.49 C.64
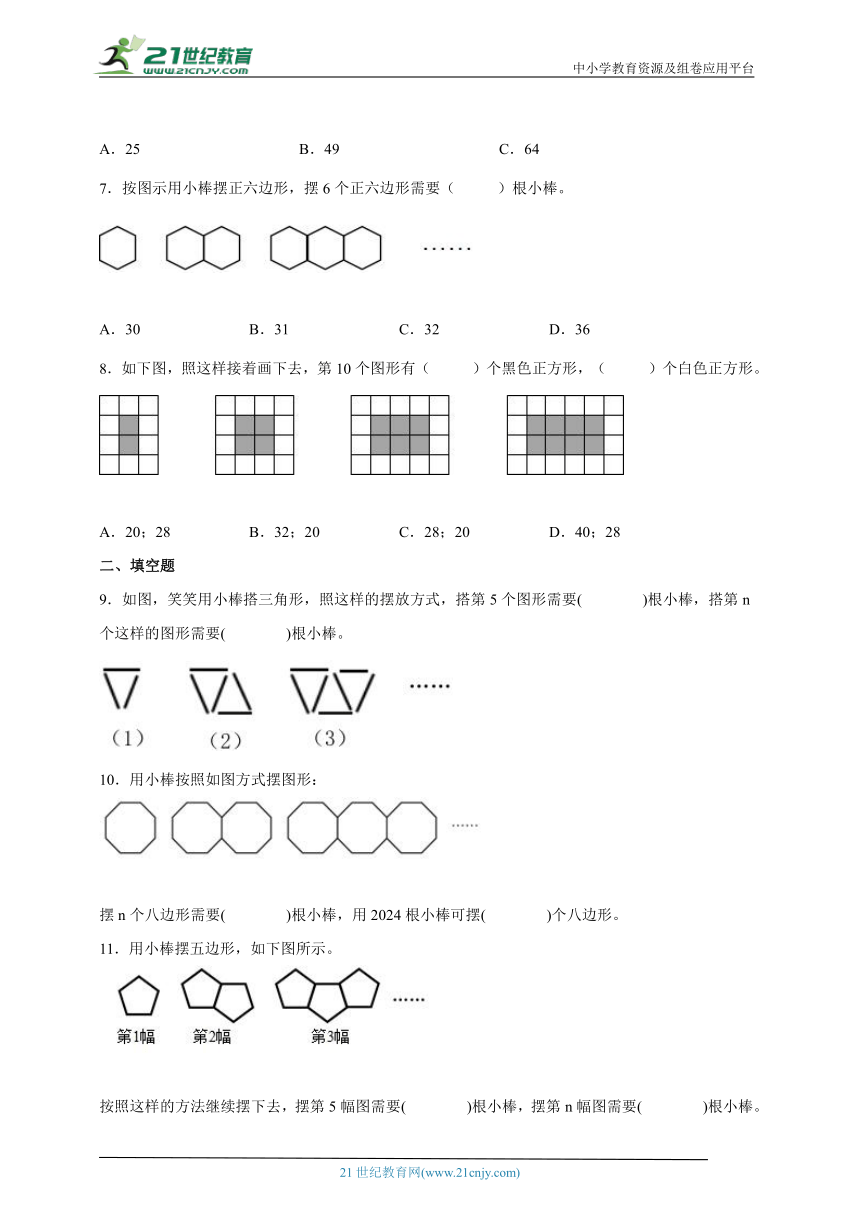
7.按图示用小棒摆正六边形,摆6个正六边形需要( )根小棒。
A.30 B.31 C.32 D.36
8.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
二、填空题
9.如图,笑笑用小棒搭三角形,照这样的摆放方式,搭第5个图形需要( )根小棒,搭第n个这样的图形需要( )根小棒。
10.用小棒按照如图方式摆图形:
摆n个八边形需要( )根小棒,用2024根小棒可摆( )个八边形。
11.用小棒摆五边形,如下图所示。
按照这样的方法继续摆下去,摆第5幅图需要( )根小棒,摆第n幅图需要( )根小棒。
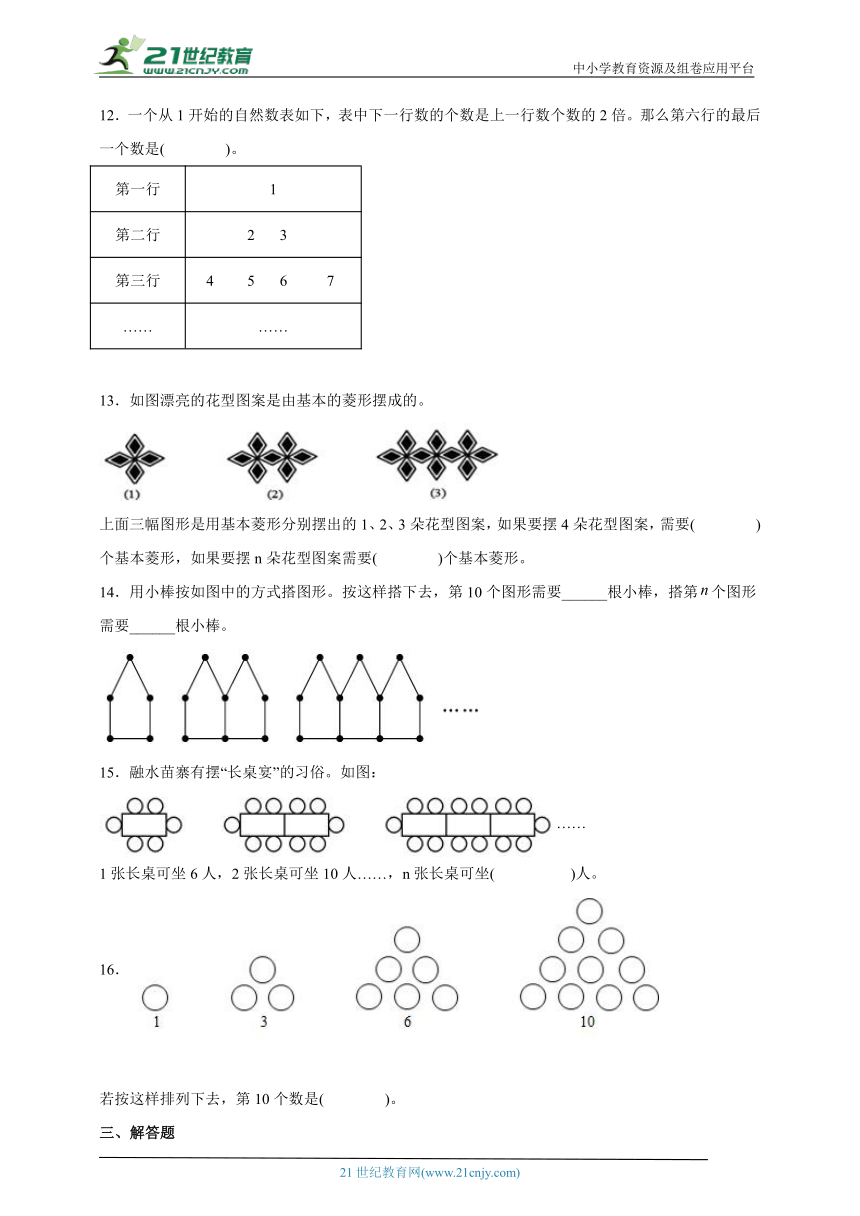
12.一个从1开始的自然数表如下,表中下一行数的个数是上一行数个数的2倍。那么第六行的最后一个数是( )。
第一行 1
第二行 2 3
第三行 4 5 6 7
…… ……
13.如图漂亮的花型图案是由基本的菱形摆成的。
上面三幅图形是用基本菱形分别摆出的1、2、3朵花型图案,如果要摆4朵花型图案,需要( )个基本菱形,如果要摆n朵花型图案需要( )个基本菱形。
14.用小棒按如图中的方式搭图形。按这样搭下去,第10个图形需要______根小棒,搭第个图形需要______根小棒。
15.融水苗寨有摆“长桌宴”的习俗。如图:
……
1张长桌可坐6人,2张长桌可坐10人……,n张长桌可坐( )人。
16.
若按这样排列下去,第10个数是( )。
三、解答题
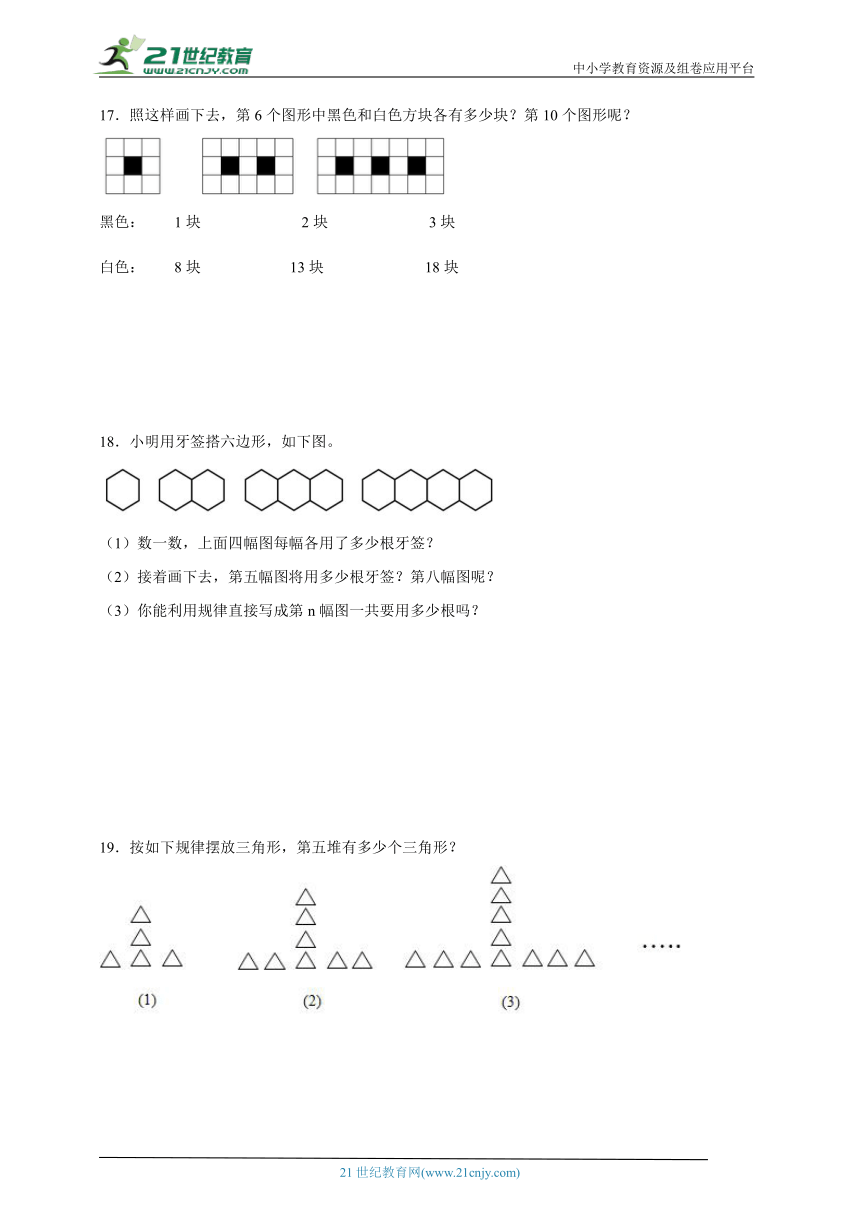
17.照这样画下去,第6个图形中黑色和白色方块各有多少块?第10个图形呢?
黑色: 1块 2块 3块
白色: 8块 13块 18块
18.小明用牙签搭六边形,如下图。
(1)数一数,上面四幅图每幅各用了多少根牙签?
(2)接着画下去,第五幅图将用多少根牙签?第八幅图呢?
(3)你能利用规律直接写成第n幅图一共要用多少根吗?
19.按如下规律摆放三角形,第五堆有多少个三角形?
20.用小棒摆正方形,列表如下:
正方形个数 摆成的图形 小棒的根数
1 4
2 7
3 10
4 13
…… …… ……
(1)每多摆1个正方形,就增加( )根小棒。
(2)摆20个正方形需要多少根小棒?
21.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有多少个菱形?第幅图中有多少个菱形?
参考答案:
1.A
【解析】
【分析】
由图可知,每增加一个小正方形增加3根小棒,第1个图形需要4根小棒,第2个图形需要4+3根小棒,第3个图形需要4+3×2根小棒,第4个图形需要4+3×3根小棒,第5个图形需要4+3×4根小棒……,以此类推。
【详解】
第n个图形需要小棒的根数表示为:4+3×(n-1)
=4+3n-3
=3n+1
故答案为:A
【点睛】
分析题意找出图形变化的规律是解答题目的关键。
2.B
【解析】
【分析】
根据上图意可知,第一个图形用3根小棒,第二个图形用5根小棒,第三个图形用7根小棒,第四个图形用9根小棒…第n个图形需要小棒的根数是2n+1。
【详解】
由分析得,
发现:每增加一个三角形就增加2根小棒,所以第n个图形需要小棒的根数是2n+1。
故选:B
【点睛】
此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
3.C
【解析】
【分析】
根据题意可知,每增加一个图就增加4个“●”,据此可知,第四幅图形最外圈(阴影部分)有20个“●”。
【详解】
第四幅图形最外圈(阴影部分)有20个“●”;
故答案为:C。
【点睛】
根据题图找到规律是解答本题的关键。
4.D
【解析】
【分析】
摆一个正方形需要4根小棒,可以写成:1×3+1;摆2个正方形需要7个小棒,可以写成:2×3+1;摆3个正方形需要10个小棒,可以做成:3×3+1;…由此可以推理得出一般规律解答问题。
【详解】
由分析可知,摆1个图形需要小棒数量:1×3+1;
摆2个图形需要小棒数量:2×3+1;
摆3个图形需要小棒数量:3×3+1;
由此可知摆n个图形需要小棒的数量:3n+1
当摆10个正方形图形,即n=10,代入式子:
3×10+1
=30+1
=31(根)
故答案选:D
【点睛】
根据题干已知的图形的排列特点以及数量关系,推理得出一般的结论进行解答,是此类问题的关键。
5.D
【解析】
【分析】
第1个图形中三角形的个数是4个, 第2个图形中三角形的个数是8个,第3个图形中三角形的个数是12个,第n个图形中三角形的个数是4n。
【详解】
第1个图形中三角形的个数是4=4×1(个),
第2个图形中三角形的个数是8=4×2(个),
第3个图形中三角形的个数是12=4×3(个),
…
第n个图形中三角形的个数是4n=4×n(个)
故选:D
【点睛】
此题考查的是找规律,解答此题的关键是根据图找出规律并用规律解决问题。
6.B
【解析】
【分析】
由图可知,第1个图形有1行共1个小三角形;
第2个图形有2行共(1+3)个小三角形;
第3个图形有3行共(1+3+5)个小三角形;
第4个图形有4行共(1+3+5+7)个小三角形;
第5个图形有5行共(1+3+5+7+9)个小三角形;
第6个图形有6行共(1+3+5+7+9+11)个小三角形;
第7个图形有7行共(1+3+5+7+9+11+13)个小三角形;据此解答。
【详解】
分析可知,第7个图形小三角形的个数为:1+3+5+7+9+11+13=72=49
故答案为:B
【点睛】
从1开始n个连续奇数相加的和等于n2。
7.B
【解析】
【分析】
观察图形:第一个图形需要6根小棒,第二个图形需要11根小棒,第三个图形需要16根小棒......可发现每一个图形所需要的小棒数满足:第n个图形需要5n+1根小棒。所以第6个图形所需小棒数为:5×6+1=31(根)。
【详解】
5×6+1
=30+1
=31(根)
所以,摆6个正六边形需要31根小棒。
故答案为:B
【点睛】
认真观察图形发现其变化规律:每一个图形所需要的小棒数满足:第n个图形需要5n+1根小棒;这是解答此题的关键。
8.A
【解析】
【分析】
分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】
第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】
用含有字母的式子表示出图形变化的规律是解答题目的关键。
9. 11 2n+1
【解析】
【分析】
看图,第一个三角形需要2×1+1=3(根)小棒,第二个三角形需要2×2+1=5(根)小棒,第三个三角形需要2×3+1=7(根)小棒,合理推测,第五个三角形需要2×5+1=11(根)小棒,第n个三角形需要(2×n+1)根小棒。
【详解】
2×5+1
=10+1
=11(根)
2×n+1=2n+1
所以,搭第5个图形需要11根小棒,搭第n个这样的图形需要(2n+1)根小棒。
【点睛】
本题考查了数与形,有一定观察和归纳总结能力是解题的关键。
10. (7n+1) 289
【解析】
【分析】
摆1个八边形需要的小棒数为8根,即7×1+1;
摆2个八边形需要的小棒数为15根,即7×2+1;
摆3个八边形需要的小棒数为22根,即7×3+1;
……
摆n个八边形需要的小棒数为:7n+1。
【详解】
由已知图形可得需要小棒根数依次是8、15、22,即相邻的两个数后面的比前面的多7,则摆n个八边形需要小棒:8+(n-1)×7=7n+1
7n+1=2024
7n=2023
n=289
即用2024根小棒可摆289个八边形。
【点睛】
根据图形规律找出第n个图形小棒根数的表达式是解答本题的关键。
11. 21 4n+1
【解析】
【分析】
第1幅图需要的小棒数为5根,即:4×1+1;第2幅图需要的小棒数为9根,即::4×2+1;第3幅图需要的小棒数为13根,即:4×3+1;……第n幅图需要的小棒数为: 4n+1;据此填空即可。
【详解】
根据分析可得:
4×5+1
=20+1
=21(个)
所以,按照这样的方法继续摆下去,摆第5幅图需要21根小棒,摆第n幅图需要(4n+1)根小棒。
【点睛】
本题主要考查数与形结合的规律,发现每多1个幅图就多4根小棒是解本题的关键。
12.63
【解析】
【分析】
通过观察分析可知,表中下一行中数的个数是上一行中数的个数的2倍,所以第n行的数字的个数为个,又每一行中最后一个数为前边从第一行到这一行中所有字的个数,如第三行中最后一个数为7,则一至三行中共有7个数字,由此可知,到第n行中最后一个数字为1+2+4+…+。
【详解】
===2×2×2×2×2=32
1+2+4+8+16+32=63
【点睛】
寻找数字排列中的规律,平时要注重多积累,培养数感。
13. 13 (3n+1)
【解析】
【分析】
摆1朵花型图案,需要的基本菱形有4个,即3×1+1;
摆2朵花型图案,需要的基本菱形有7个,即3×2+1;
摆3朵花型图案,需要的基本菱形有10个,即3×3+1;
……
摆n朵花型图案,需要的基本菱形的个数为:3n+1。
【详解】
3×4+1
=12+1
=13(个)
所以,如果要摆4朵花型图案,需要13个基本菱形,如果要摆n朵花型图案需要(3n+1)个基本菱形。
【点睛】
观察分析出图形的变化规律是解题的关键,本题旨在培养学生的逻辑推理能力。
14. 41 4n+1
【解析】
【分析】
观察可知,小棒数量=五边形数量×4+1,据此分析。
【详解】
10×4+1
=40+1
=41(根)
n×4+1=4n+1(根)
【点睛】
数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
15.2+4n
【解析】
【分析】
1张长桌可坐6人,6=2+1×4;2张长桌可坐10人,10= 2+2×4;3张长桌可坐14人,14= 2+3×4;n张长桌可坐的人数:2+4n。
【详解】
根据分析可知,n张长桌可坐(2+4n)人。
【点睛】
本题主要考查数与形结合的规律,发现每多1张桌子就多坐4人是解本题的关键。
16.55
【解析】
【分析】
观察所给出的数列知道,从第二个数起,每一个数分别是它前面的数加1、2、3、4、5、6…等自然数所得,由此得出答案。
【详解】
0+1=1
1+2=3
3+3=6
6+4=10
10+5=15
15+6=21
21+7=28
28+8=36
36+9=45
45+10=55
【点睛】
此题考查了数列中的规律,认真观察,找出规律是解决此题的关键。
17.6块,33块;10块,53块
【解析】
【分析】
根据第几个图形
1 2 3 4 n
黑色:1块 2块 3块 4块 n块
白色:8块 13块 18块 23块 (3+5n)块
3+5×1 3+5×2 3+5×3 3+5×4 3+5n
所以,第6个图形中黑色有6块,白色方块有33块;第10个图形中黑色有10块,白色方块有53块。
【详解】
由分析得,
第6个图形中黑色有6块,白色方块有:
3+5×6
=3+30
=33(块)
第10个图形中黑色有10块,白色方块有:
3+5×10
=3+50
=53(块)
【点睛】
此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
18.(1)6根;11根;16根;21根;
(2)26根;41根;
(3)(5n+1)根
【解析】
【分析】
分析图形可知,每增加一个六边形就增加5根牙签,第1个图形一共用了6根牙签,第2个图形一共用了(6+5)根牙签,第3个图形一共用了(6+5×2)根牙签,第4个图形一共用了(6+5×3)根牙签……则第n个图形一共用了[6+5×(n-1)]根牙签,据此解答。
【详解】
(1)第1幅图用了6根,第2幅图用了11根,第3幅图用了16根,第4幅图用了21根。
(2)第5幅图:6+5×(5-1)
=6+5×4
=6+20
=26(根)
第8幅图:6+5×(8-1)
=6+40-5
=46-5
=41(根)
答:第五幅图将用26根牙签,第八幅图将用41根牙签。
(3)6+5×(n-1)
=6+5n-5
=(5n+1)根
答:第n幅图一共要用(5n+1)根。
【点睛】
用含有字母的式子表示出图形变化的规律是解答题目的关键。
19.17个
【解析】
【分析】
这是一组等差数列,公差是3,从左到右依次加3。第1堆,5个△,5=3×1+2;第2堆,8个△,8=3×2+2;第3堆,11个△,11=3×3+2…第n堆,(3n+2)个△。
【详解】
第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△。
当n=5时,
3×5+2
=15+2
=17(个)
答:第五堆有17个三角形。
【点睛】
此题考查的是找规律,解答此题的关键是找到规律后,再根据规律解答就比较容易了。
20.(1)3;
(2)61根
【解析】
【分析】
由列表可知,摆1个小正方形需要4根小棒;摆2个小正方形需要(4+3)根小棒;摆3个小正方形需要(4+3+3)根小棒;摆4个小正方形需要(4+3+3+3)根小棒……
摆n个小正方形需要4+(n-1)×3根小棒;把n=20代入含有字母的式子计算出结果即可。
【详解】
(1)每多摆1个正方形,就增加(3)根小棒。
(2)分析可知摆n个小正方形需要4+(n-1)×3=3n+1根小棒
当n=20时
3n+1=3×20+1=61(根)
答:摆20个正方形需要61根小棒。
【点睛】
分析列表找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
21.7个;(2n-1)个
【解析】
【分析】
根据图意,第1幅图中有1个菱形,第二个图中有3=2×2-1,第三个图中有5=2×3-1,第4幅图有7=2×4-1,以此类推,则第n个图中,有(2n-1)个菱形。注意分析菱形的个数与第几个图形的对应关系。
【详解】
由分析可知:
则第4幅图中有:
2×4-1
=8-1
=7(个)
则第n个图中,有(2n-1)个菱形。
【点睛】
此题考查的是找规律,关键是通过归纳与总结,得到其中的规律并运用规律。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数与形高频考点检测卷(单元测试)-小学数学六年级上册人教版
一、选择题
1.如图,用同样的小棒去摆,第n个图形需要小棒的根数表示错误的式子是( )。
A.4n-1 B.4+ 3(n-1) C.3n+1
2.如图,用同样的小棒去摆,第n个图形需要小棒的根数是( )。
A.3n B.2n+1 C.3n-1
3.第四幅图形最外圈(阴影部分)有( )个“●”。
A.36 B.25 C.20
4.摆一个正方形需要4根小棒,以后每加一个正方形需要加3根小棒,按此方法,摆10个正方形共需( )根小棒。
A.27 B.30 C.40 D.31
5.观察下列图形,则第n个图形中三角形的个数是( )。
A. B. C. D.
6.仔细分析,第7个图形一共有( )个小三角形。
A.25 B.49 C.64
7.按图示用小棒摆正六边形,摆6个正六边形需要( )根小棒。
A.30 B.31 C.32 D.36
8.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
二、填空题
9.如图,笑笑用小棒搭三角形,照这样的摆放方式,搭第5个图形需要( )根小棒,搭第n个这样的图形需要( )根小棒。
10.用小棒按照如图方式摆图形:
摆n个八边形需要( )根小棒,用2024根小棒可摆( )个八边形。
11.用小棒摆五边形,如下图所示。
按照这样的方法继续摆下去,摆第5幅图需要( )根小棒,摆第n幅图需要( )根小棒。
12.一个从1开始的自然数表如下,表中下一行数的个数是上一行数个数的2倍。那么第六行的最后一个数是( )。
第一行 1
第二行 2 3
第三行 4 5 6 7
…… ……
13.如图漂亮的花型图案是由基本的菱形摆成的。
上面三幅图形是用基本菱形分别摆出的1、2、3朵花型图案,如果要摆4朵花型图案,需要( )个基本菱形,如果要摆n朵花型图案需要( )个基本菱形。
14.用小棒按如图中的方式搭图形。按这样搭下去,第10个图形需要______根小棒,搭第个图形需要______根小棒。
15.融水苗寨有摆“长桌宴”的习俗。如图:
……
1张长桌可坐6人,2张长桌可坐10人……,n张长桌可坐( )人。
16.
若按这样排列下去,第10个数是( )。
三、解答题
17.照这样画下去,第6个图形中黑色和白色方块各有多少块?第10个图形呢?
黑色: 1块 2块 3块
白色: 8块 13块 18块
18.小明用牙签搭六边形,如下图。
(1)数一数,上面四幅图每幅各用了多少根牙签?
(2)接着画下去,第五幅图将用多少根牙签?第八幅图呢?
(3)你能利用规律直接写成第n幅图一共要用多少根吗?
19.按如下规律摆放三角形,第五堆有多少个三角形?
20.用小棒摆正方形,列表如下:
正方形个数 摆成的图形 小棒的根数
1 4
2 7
3 10
4 13
…… …… ……
(1)每多摆1个正方形,就增加( )根小棒。
(2)摆20个正方形需要多少根小棒?
21.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有多少个菱形?第幅图中有多少个菱形?
参考答案:
1.A
【解析】
【分析】
由图可知,每增加一个小正方形增加3根小棒,第1个图形需要4根小棒,第2个图形需要4+3根小棒,第3个图形需要4+3×2根小棒,第4个图形需要4+3×3根小棒,第5个图形需要4+3×4根小棒……,以此类推。
【详解】
第n个图形需要小棒的根数表示为:4+3×(n-1)
=4+3n-3
=3n+1
故答案为:A
【点睛】
分析题意找出图形变化的规律是解答题目的关键。
2.B
【解析】
【分析】
根据上图意可知,第一个图形用3根小棒,第二个图形用5根小棒,第三个图形用7根小棒,第四个图形用9根小棒…第n个图形需要小棒的根数是2n+1。
【详解】
由分析得,
发现:每增加一个三角形就增加2根小棒,所以第n个图形需要小棒的根数是2n+1。
故选:B
【点睛】
此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
3.C
【解析】
【分析】
根据题意可知,每增加一个图就增加4个“●”,据此可知,第四幅图形最外圈(阴影部分)有20个“●”。
【详解】
第四幅图形最外圈(阴影部分)有20个“●”;
故答案为:C。
【点睛】
根据题图找到规律是解答本题的关键。
4.D
【解析】
【分析】
摆一个正方形需要4根小棒,可以写成:1×3+1;摆2个正方形需要7个小棒,可以写成:2×3+1;摆3个正方形需要10个小棒,可以做成:3×3+1;…由此可以推理得出一般规律解答问题。
【详解】
由分析可知,摆1个图形需要小棒数量:1×3+1;
摆2个图形需要小棒数量:2×3+1;
摆3个图形需要小棒数量:3×3+1;
由此可知摆n个图形需要小棒的数量:3n+1
当摆10个正方形图形,即n=10,代入式子:
3×10+1
=30+1
=31(根)
故答案选:D
【点睛】
根据题干已知的图形的排列特点以及数量关系,推理得出一般的结论进行解答,是此类问题的关键。
5.D
【解析】
【分析】
第1个图形中三角形的个数是4个, 第2个图形中三角形的个数是8个,第3个图形中三角形的个数是12个,第n个图形中三角形的个数是4n。
【详解】
第1个图形中三角形的个数是4=4×1(个),
第2个图形中三角形的个数是8=4×2(个),
第3个图形中三角形的个数是12=4×3(个),
…
第n个图形中三角形的个数是4n=4×n(个)
故选:D
【点睛】
此题考查的是找规律,解答此题的关键是根据图找出规律并用规律解决问题。
6.B
【解析】
【分析】
由图可知,第1个图形有1行共1个小三角形;
第2个图形有2行共(1+3)个小三角形;
第3个图形有3行共(1+3+5)个小三角形;
第4个图形有4行共(1+3+5+7)个小三角形;
第5个图形有5行共(1+3+5+7+9)个小三角形;
第6个图形有6行共(1+3+5+7+9+11)个小三角形;
第7个图形有7行共(1+3+5+7+9+11+13)个小三角形;据此解答。
【详解】
分析可知,第7个图形小三角形的个数为:1+3+5+7+9+11+13=72=49
故答案为:B
【点睛】
从1开始n个连续奇数相加的和等于n2。
7.B
【解析】
【分析】
观察图形:第一个图形需要6根小棒,第二个图形需要11根小棒,第三个图形需要16根小棒......可发现每一个图形所需要的小棒数满足:第n个图形需要5n+1根小棒。所以第6个图形所需小棒数为:5×6+1=31(根)。
【详解】
5×6+1
=30+1
=31(根)
所以,摆6个正六边形需要31根小棒。
故答案为:B
【点睛】
认真观察图形发现其变化规律:每一个图形所需要的小棒数满足:第n个图形需要5n+1根小棒;这是解答此题的关键。
8.A
【解析】
【分析】
分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】
第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】
用含有字母的式子表示出图形变化的规律是解答题目的关键。
9. 11 2n+1
【解析】
【分析】
看图,第一个三角形需要2×1+1=3(根)小棒,第二个三角形需要2×2+1=5(根)小棒,第三个三角形需要2×3+1=7(根)小棒,合理推测,第五个三角形需要2×5+1=11(根)小棒,第n个三角形需要(2×n+1)根小棒。
【详解】
2×5+1
=10+1
=11(根)
2×n+1=2n+1
所以,搭第5个图形需要11根小棒,搭第n个这样的图形需要(2n+1)根小棒。
【点睛】
本题考查了数与形,有一定观察和归纳总结能力是解题的关键。
10. (7n+1) 289
【解析】
【分析】
摆1个八边形需要的小棒数为8根,即7×1+1;
摆2个八边形需要的小棒数为15根,即7×2+1;
摆3个八边形需要的小棒数为22根,即7×3+1;
……
摆n个八边形需要的小棒数为:7n+1。
【详解】
由已知图形可得需要小棒根数依次是8、15、22,即相邻的两个数后面的比前面的多7,则摆n个八边形需要小棒:8+(n-1)×7=7n+1
7n+1=2024
7n=2023
n=289
即用2024根小棒可摆289个八边形。
【点睛】
根据图形规律找出第n个图形小棒根数的表达式是解答本题的关键。
11. 21 4n+1
【解析】
【分析】
第1幅图需要的小棒数为5根,即:4×1+1;第2幅图需要的小棒数为9根,即::4×2+1;第3幅图需要的小棒数为13根,即:4×3+1;……第n幅图需要的小棒数为: 4n+1;据此填空即可。
【详解】
根据分析可得:
4×5+1
=20+1
=21(个)
所以,按照这样的方法继续摆下去,摆第5幅图需要21根小棒,摆第n幅图需要(4n+1)根小棒。
【点睛】
本题主要考查数与形结合的规律,发现每多1个幅图就多4根小棒是解本题的关键。
12.63
【解析】
【分析】
通过观察分析可知,表中下一行中数的个数是上一行中数的个数的2倍,所以第n行的数字的个数为个,又每一行中最后一个数为前边从第一行到这一行中所有字的个数,如第三行中最后一个数为7,则一至三行中共有7个数字,由此可知,到第n行中最后一个数字为1+2+4+…+。
【详解】
===2×2×2×2×2=32
1+2+4+8+16+32=63
【点睛】
寻找数字排列中的规律,平时要注重多积累,培养数感。
13. 13 (3n+1)
【解析】
【分析】
摆1朵花型图案,需要的基本菱形有4个,即3×1+1;
摆2朵花型图案,需要的基本菱形有7个,即3×2+1;
摆3朵花型图案,需要的基本菱形有10个,即3×3+1;
……
摆n朵花型图案,需要的基本菱形的个数为:3n+1。
【详解】
3×4+1
=12+1
=13(个)
所以,如果要摆4朵花型图案,需要13个基本菱形,如果要摆n朵花型图案需要(3n+1)个基本菱形。
【点睛】
观察分析出图形的变化规律是解题的关键,本题旨在培养学生的逻辑推理能力。
14. 41 4n+1
【解析】
【分析】
观察可知,小棒数量=五边形数量×4+1,据此分析。
【详解】
10×4+1
=40+1
=41(根)
n×4+1=4n+1(根)
【点睛】
数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
15.2+4n
【解析】
【分析】
1张长桌可坐6人,6=2+1×4;2张长桌可坐10人,10= 2+2×4;3张长桌可坐14人,14= 2+3×4;n张长桌可坐的人数:2+4n。
【详解】
根据分析可知,n张长桌可坐(2+4n)人。
【点睛】
本题主要考查数与形结合的规律,发现每多1张桌子就多坐4人是解本题的关键。
16.55
【解析】
【分析】
观察所给出的数列知道,从第二个数起,每一个数分别是它前面的数加1、2、3、4、5、6…等自然数所得,由此得出答案。
【详解】
0+1=1
1+2=3
3+3=6
6+4=10
10+5=15
15+6=21
21+7=28
28+8=36
36+9=45
45+10=55
【点睛】
此题考查了数列中的规律,认真观察,找出规律是解决此题的关键。
17.6块,33块;10块,53块
【解析】
【分析】
根据第几个图形
1 2 3 4 n
黑色:1块 2块 3块 4块 n块
白色:8块 13块 18块 23块 (3+5n)块
3+5×1 3+5×2 3+5×3 3+5×4 3+5n
所以,第6个图形中黑色有6块,白色方块有33块;第10个图形中黑色有10块,白色方块有53块。
【详解】
由分析得,
第6个图形中黑色有6块,白色方块有:
3+5×6
=3+30
=33(块)
第10个图形中黑色有10块,白色方块有:
3+5×10
=3+50
=53(块)
【点睛】
此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
18.(1)6根;11根;16根;21根;
(2)26根;41根;
(3)(5n+1)根
【解析】
【分析】
分析图形可知,每增加一个六边形就增加5根牙签,第1个图形一共用了6根牙签,第2个图形一共用了(6+5)根牙签,第3个图形一共用了(6+5×2)根牙签,第4个图形一共用了(6+5×3)根牙签……则第n个图形一共用了[6+5×(n-1)]根牙签,据此解答。
【详解】
(1)第1幅图用了6根,第2幅图用了11根,第3幅图用了16根,第4幅图用了21根。
(2)第5幅图:6+5×(5-1)
=6+5×4
=6+20
=26(根)
第8幅图:6+5×(8-1)
=6+40-5
=46-5
=41(根)
答:第五幅图将用26根牙签,第八幅图将用41根牙签。
(3)6+5×(n-1)
=6+5n-5
=(5n+1)根
答:第n幅图一共要用(5n+1)根。
【点睛】
用含有字母的式子表示出图形变化的规律是解答题目的关键。
19.17个
【解析】
【分析】
这是一组等差数列,公差是3,从左到右依次加3。第1堆,5个△,5=3×1+2;第2堆,8个△,8=3×2+2;第3堆,11个△,11=3×3+2…第n堆,(3n+2)个△。
【详解】
第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△。
当n=5时,
3×5+2
=15+2
=17(个)
答:第五堆有17个三角形。
【点睛】
此题考查的是找规律,解答此题的关键是找到规律后,再根据规律解答就比较容易了。
20.(1)3;
(2)61根
【解析】
【分析】
由列表可知,摆1个小正方形需要4根小棒;摆2个小正方形需要(4+3)根小棒;摆3个小正方形需要(4+3+3)根小棒;摆4个小正方形需要(4+3+3+3)根小棒……
摆n个小正方形需要4+(n-1)×3根小棒;把n=20代入含有字母的式子计算出结果即可。
【详解】
(1)每多摆1个正方形,就增加(3)根小棒。
(2)分析可知摆n个小正方形需要4+(n-1)×3=3n+1根小棒
当n=20时
3n+1=3×20+1=61(根)
答:摆20个正方形需要61根小棒。
【点睛】
分析列表找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
21.7个;(2n-1)个
【解析】
【分析】
根据图意,第1幅图中有1个菱形,第二个图中有3=2×2-1,第三个图中有5=2×3-1,第4幅图有7=2×4-1,以此类推,则第n个图中,有(2n-1)个菱形。注意分析菱形的个数与第几个图形的对应关系。
【详解】
由分析可知:
则第4幅图中有:
2×4-1
=8-1
=7(个)
则第n个图中,有(2n-1)个菱形。
【点睛】
此题考查的是找规律,关键是通过归纳与总结,得到其中的规律并运用规律。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
