(2022秋新教材)第八单元数学广角——数与形经典题型练习卷(单元测试) 小学数学六年级上册人教版(含答案)
文档属性
| 名称 | (2022秋新教材)第八单元数学广角——数与形经典题型练习卷(单元测试) 小学数学六年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八单元数与形经典题型练习卷(单元测试)-小学数学六年级上册人教版
题号 一 二 三 总分
得分
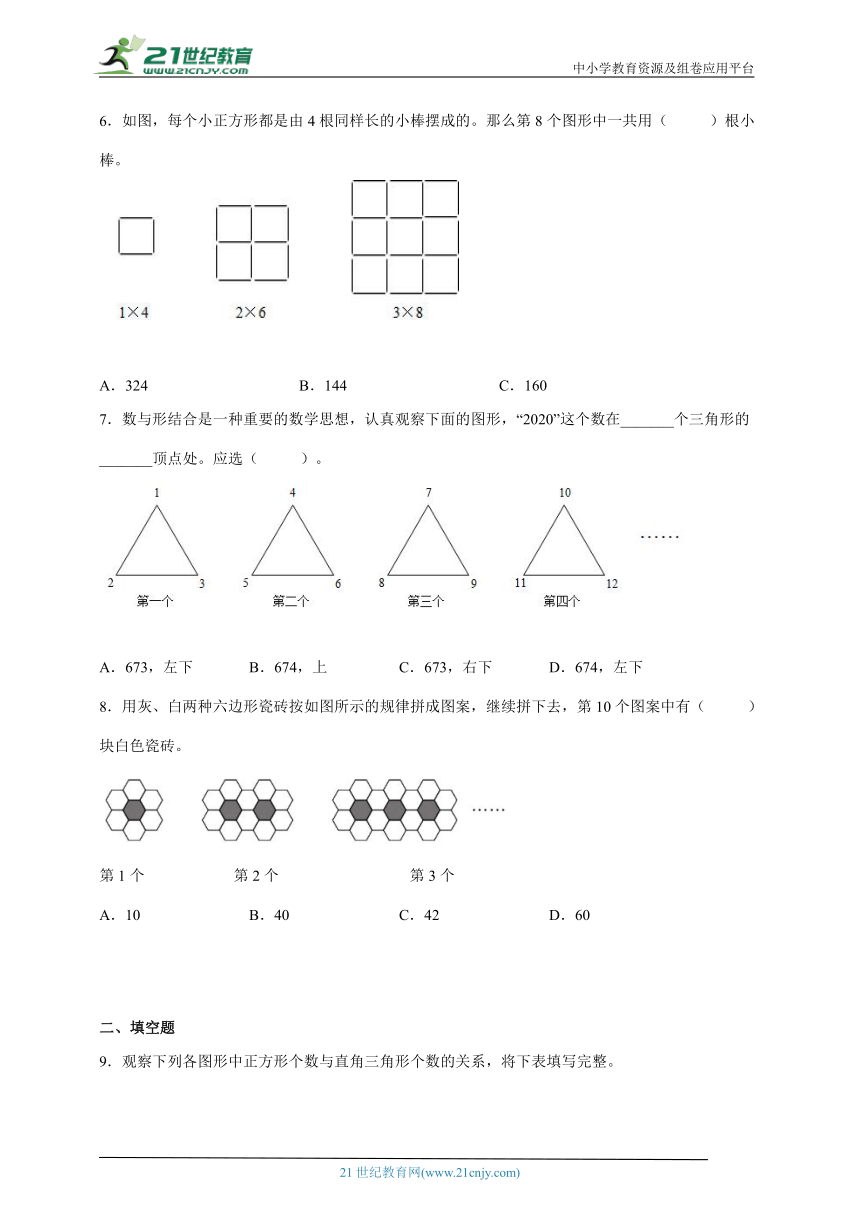
一、选择题
1.用小棒搭正方形,搭n个这样的正方形需要( )根小棒。
A. B. C.
2.照下面这样摆下去,摆n个三角形需要( )根火柴棒。
A.3n B.3n-1 C.2n+1 D.2n+3
3.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
4.与的结果相同的是( )。
A.5×3 B. C. D.
5.找规律:3,7,15, …… 应填几,正确的是( )。
A.3×2+1=7,7×2+1=15,15×2+1=31,填31
B.3+4×1=7,7+4×2=15,15+15×3=60 ,填60
C.必须要写出4个数才能找出规律,“”里无法填出唯一的数
6.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
7.数与形结合是一种重要的数学思想,认真观察下面的图形,“2020”这个数在_______个三角形的_______顶点处。应选( )。
A.673,左下 B.674,上 C.673,右下 D.674,左下
8.用灰、白两种六边形瓷砖按如图所示的规律拼成图案,继续拼下去,第10个图案中有( )块白色瓷砖。
第1个 第2个 第3个
A.10 B.40 C.42 D.60
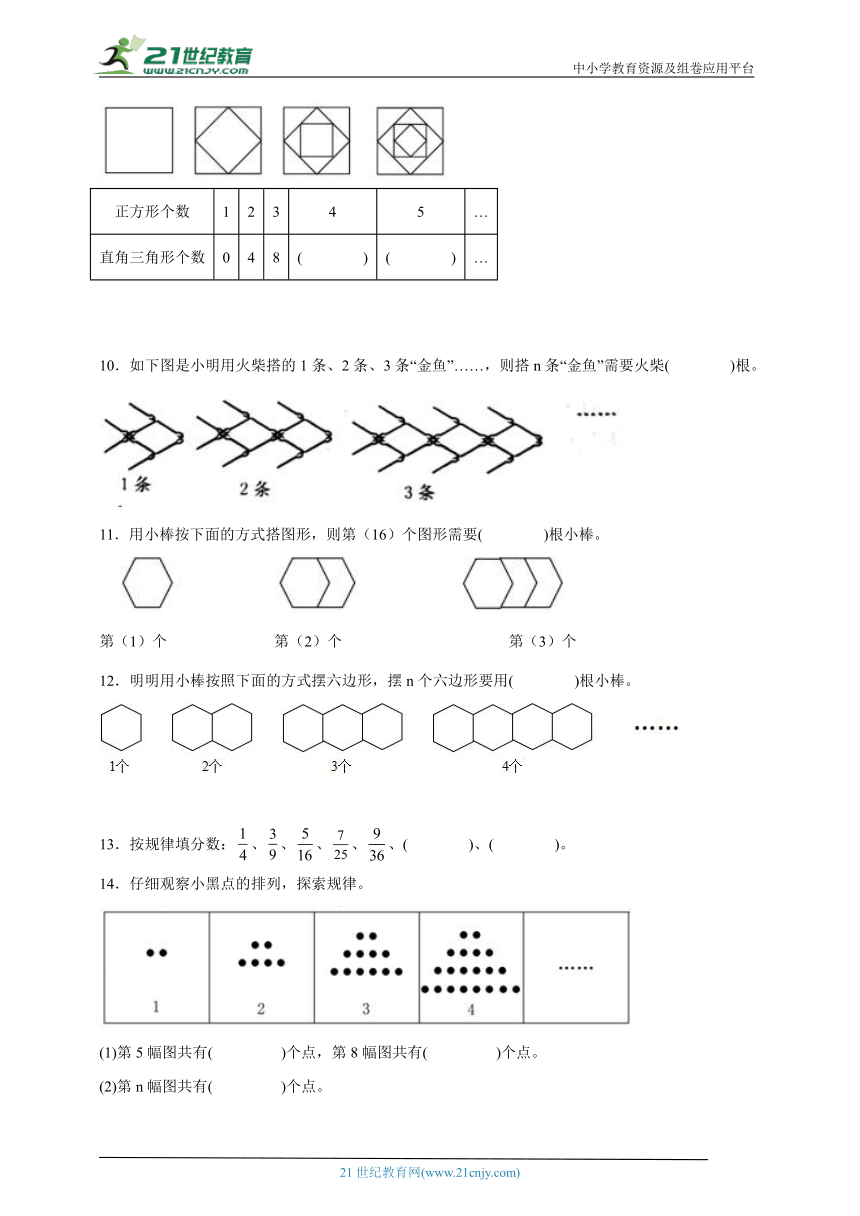
二、填空题
9.观察下列各图形中正方形个数与直角三角形个数的关系,将下表填写完整。
正方形个数 1 2 3 4 5 …
直角三角形个数 0 4 8 ( ) ( ) …
10.如下图是小明用火柴搭的1条、2条、3条“金鱼”……,则搭n条“金鱼”需要火柴( )根。
11.用小棒按下面的方式搭图形,则第(16)个图形需要( )根小棒。
第(1)个 第(2)个 第(3)个
12.明明用小棒按照下面的方式摆六边形,摆n个六边形要用( )根小棒。
13.按规律填分数:、、、、、( )、( )。
14.仔细观察小黑点的排列,探索规律。
(1)第5幅图共有( )个点,第8幅图共有( )个点。
(2)第n幅图共有( )个点。
15.如图:……正方形按照这样的规律变换,当正方形有n个时,三角形有( )个。
16.找规律,写答案。
0.1÷11=0.0090909……
0.2÷11=0.0181818……
0.3÷11=0.0272727……
0.5÷11=( )
找一找,这个商的小数点后第2022个数字是( )。
三、解答题
17.
(1)像这样摆下去,第n个图形需要__________根小棒。
(2)当n=35时,计算第(1)题式子中需要的小棒数。
18.按如下规律摆放三角形,第五堆有多少个三角形?
19.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
20.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
21.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点……按此规律第10个图中共有多少个点?第100个图形呢?
22.想一想,画一画,这样的4张桌子连在一起共可以坐多少人?n张呢?
23.如下图,1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么10个这样的杯子叠起来的高度是多少厘米?
24.观察算式的规律:,,,,……。用含字母的式子表示规律:( )。
用规律计算:( )。
参考答案:
1.C
【分析】观察可知,小棒数量=正方形数量×3+1,据此分析。
【详解】n×3+1=3n+1(根)
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
2.C
【分析】分析图形可知,摆1个三角形需要3根火柴棒,摆2个三角形需要(3+2)根火柴棒,摆3个三角形需要(3+2+2)根火柴棒……每增加1个三角形就增加2根火柴棒,则摆n个三角形需要3+2(n-1)根火柴棒,据此解答。
【详解】摆n个三角形需要火柴棒的根数:3+2(n-1)=3+2n-2=2n+1
故答案为:C
【点睛】找出图形变化的规律是解答题目的关键。
3.A
【分析】分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】用含有字母的式子表示出图形变化的规律是解答题目的关键。
4.C
【分析】个连续奇数相加的和结果为,把拆为几个连续奇数相加的形式,利用公式即可求得。
【详解】
=34
故答案为:C
【点睛】本题考查数形结合思想在计算题中的应用。
5.C
【分析】结合题意,一一分析各个选项的正误,从而选出正确选项。
【详解】根据3,7,15, ……,可以至少得出两个符合它的规律,分别是A和B选项中的规律。那么可推出,必须要写出4个数才能找出确定的规律,那么“”里无法填出唯一的数。
故答案为:C
【点睛】本题考查了找规律,能从数字排列中找出规律是解题的关键。
6.B
【分析】根据上图中已知的规律:图形边长×边数,继续排列出第8个图形中一共有8×18根小棒。
【详解】图1有1×4
图2有2×6
图3有3×8
图4有4×10
图5有5×12
图6有6×14
图7有7×16
图8有8×18=144(根)
故选:B
【点睛】此题考查的是数形结合,关键是找出规律,再用规律解决问题。
7.B
【分析】从上图中发现:每一个三角形有3个顶点,用2020÷3=673(个)……1(个)也就是在第673个三角形后还余1个顶点,1个顶点正好在第674个三角形的上顶点处。
【详解】由分析可得,
2020÷3=673(个)……1(个)
所以,“2020”这个数在674个三角形的上顶点处。
故选:B
【点睛】此题考查的是数与形结合找规律,找出规律是解题关键。
8.C
【分析】观察图形发现,第一个图案有白色地砖6块,后边每多一个图案,则多4块白色地砖,根据这个规律,可确定第n个图案中有白色地砖的数量。
【详解】结合图形,第一个图案有白色地砖6块,后边每多一个图案,则多4块白色地砖,根据这个规律,可确定第n个图案中有白色地砖:4n+2块,
第10个图案中有白色瓷砖:
4×10+2
=40+2
=42(块)
故选:C
【点睛】本题考查的是图形的变化类问题,解题关键是图形结合,发现规律。
9. 12 16
【分析】经观察发现,每多1个正方形就多4个直角三角形,据此解答。
【详解】8+4=12(个)
12+4=16(个)
【点睛】本题主要考查数与形结合的规律,发现每多1个正方形就多4个直角三角形是解本题的关键。
10.6n+2
【分析】观察图形发现:搭1条金鱼需要火柴8根,搭2条金鱼需要14根,即发现了每多搭1条金鱼,需要多用6根火柴,则搭n条“金鱼”需要火柴8+6(n-1)=6n+2,据此即可解答问题。
【详解】根据分析得,每多搭一条金鱼,需要多用6根火柴。
8+6×(n-1)
=8+6n-6
=6n+2
所以搭n条金鱼需要火柴(6n+2)根。
【点睛】此类题找规律的时候一定要注意结合图形进行发现规律。
11.66
【分析】第一个图形:4×1+2=6根小棒组成,第二个图形:4×2+2=10根小棒组成,第三个图形:4×3+2=14根小棒组成,……那么第16个图形:4×16+2=66根小棒组成。
【详解】第一个图形中小棒数量:
4×1+2
=4+2
=6(根)
第二个图形中小棒数量:
4×2+2
=8+2
=10(根)
第三个图形中小棒数量:
4×3+2
=12+2
=14(根)
……
第16个图形中小棒数量:
4×16+2
=64+2
=66(根)
【点睛】此题考查了学生的观察能力和归纳能力,找出图形中小棒排列的规律,是解答此题的关键。
12.5n+1
【分析】由图可知,摆1个正六边形需要6根小棒,摆2个正六边形需要(6+5)根小棒,摆3个正六边形需要(6+5×2)根小棒,摆4个正六边形需要(6+5×3)根小棒……摆n个正六边形需要6+5(n-1)根小棒,据此解答。
【详解】分析可知,摆n个正六边形需要小棒的根数为:6+5(n-1)=6+5n-5=(5n+1)根。
【点睛】分析图形找出正六边形个数和小棒根数的变化规律是解答题目的关键。
13.
【分析】观察数列可知,各分数的分子按照1、3、5、7、9排列,相邻两个数的差是2;分母分别为4=22,9=32,16=42,25=52,36=62,所以后面两个分数的分母应为72=49,82=64。据此解答即可。
【详解】9+2=11,11+2=13
72=49,82=64
、、、、、、。
【点睛】本题考查数字排列规律,发现规律,利用规律是解题的关键。
14.(1) 30 72
(2)
【分析】根据图示,这组图形的规律为:第一幅图小黑点的个数为2个;第二幅图小黑点的个数:(个;第三幅图小黑点的个数为:(个;第n幅图小黑点的个数为:个。据此解答。
(1)
第一幅图小黑点的个数为2个
第二幅图小黑点的个数:(个
第三幅图小黑点的个数为:(个
第幅图小黑点的个数为:个
(1)
(个
(个
(2)
第n幅图共有个点。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现规律,并运用规律做题。
15.4n-4
【分析】图1有1个正方形、0个三角形,图2有2个正方形、4个三角形,图3有3个正方形、8个三角形,图4有4个正方形、12个三角形……,三角形的个数=(正方形个数-1)×4;据此解答即可。
【详解】三角形的个数=(正方形个数-1)×4;当正方形有n个时,三角形的个数有:(n-1)×4=4n-4。
【点睛】探索图形的变换规律,运用图形的变换规律解答问题。
16. 0.0454545…… 4
【分析】仔细观察题中的式子可以发现:除数不变,被除数乘几,商也乘几,据此求出0.5÷11=0.0454545……;这个商的小数点后第2022个数字(总数位数循环节的位数。
【详解】0.5÷0.1=5
0.5÷11=0.0090909……×5=0.0454545……
0.5÷11的商是一个循环小数,这个循环小数的循环节是45,
(2022-1)÷2
=2021÷2
=101(组)……1(位)
余数1表示一个循环里的第1个数即4;所以这个商的小数点后第2022个数字是4。
【点睛】能发现题中的规律并利用规律求出0.5÷11的结果以及熟练掌握求循环小数第几位上数字是多少的方法是解题的关键。
17.(1)2n +1;
(2)71根
【分析】(1)观察图形可知:摆1个三角形需要3根小棒,可以写作:2×1+1;摆2个需要5根小棒,可以写作:2×2+1;摆3个需要7根小棒,可以写成:3×2+1;……摆n个三角形需要:(2n +1)根小棒。
(2) 根据第一小题的分析可知,摆n个三角形需要:(2n +1)根小棒,当n=35时,把数据代入计算,即可求当n=35时,需要小棒的数量。
【详解】(1)根据分析可知,像这样摆下去,第n个图形需要(2n+1)根小棒。
(2)35×2+1
=70+1
= 71(根)
答:摆35个三角形需要71根小棒。
【点睛】认真观察图形,并从中找出图形变化的规律,是解答此题的关键。
18.17个
【分析】这是一组等差数列,公差是3,从左到右依次加3。第1堆,5个△,5=3×1+2;第2堆,8个△,8=3×2+2;第3堆,11个△,11=3×3+2…第n堆,(3n+2)个△。
【详解】第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△。
当n=5时,
3×5+2
=15+2
=17(个)
答:第五堆有17个三角形。
【点睛】此题考查的是找规律,解答此题的关键是找到规律后,再根据规律解答就比较容易了。
19.(1)白:26个;黑:10个
(2)16
【分析】(1)第1个图形一共有(3×3)个小正方形,有1个黑色小正方形,有(3×3-1)个白色小正方形;
第2个图形一共有(3×4)个小正方形,有2个黑色小正方形,有(3×4-2)个白色小正方形;
第3个图形一共有(3×5)个小正方形,有3个黑色小正方形,有(3×3-3)个白色小正方形;
……
第n个图形一共有3(n+2)=(3n+6)个小正方形,有n个黑色小正方形,有3n+6-n=2n+6个白色小正方形;
(2)把白色小正方形的个数代入表示白色小正方形含有字母的式子,求出n的值即可。
【详解】(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
【点睛】分析图形找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
20.(1)38根;(2)2+6n;(3)336个
【分析】根据题意分析可得:搭第1个图形需8根火柴,此后,每个图形都比前一个图形多用6根,故按照上面的规律,摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根;据此解答。
【详解】(1)8+(6-1)×6
=8+5×6
=8+30
=38(根)
答:摆6个“金鱼”需要38根火柴棒。
(2)摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根;
(3)(2018-8)÷6+1
=2010÷6+1
=335+1
=336(个)
答:2018根火柴棒可以摆336个“金鱼”。
【点睛】本题是对图形变化规律的考查,查出前三个图形的火柴棒的根数,并观察出后一个图形比前一个图形多6根火柴棒是解题的关键。
21.166个;15151个
【分析】分析图形可知:第1个图形有(1+1×3)个点,第2个图形有(1+1×3+2×3)个点,第3个图形有(1+1×3+2×3+3×3)个点,……
由此规律可知第n个图形有(1+1×3+2×3+3×3+…+3n)个点,据此解答。
【详解】分析可知第n个图形有(1+1×3+2×3+3×3+…+3n)个点
当n=10时,1+1×3+2×3+3×3+…+3×10
=1+(1+2+3+…+10)×3
=1+(1+10)×10÷2×3
=1+11×10÷2×3
=1+110÷2×3
=1+55×3
=1+165
=166(个)
当n=100时,1+1×3+2×3+3×3+…+3×100
=1+(1+2+3+…+100)×3
=1+(1+100)×100÷2×3
=1+101×100÷2×3
=1+10100÷2×3
=1+5050×3
=1+15150
=15151(个)
答:第10个图中共有166个点,第100个图中共有15151个点。
【点睛】解决本题应用等差数列前n项和求和公式:(首项+末项)×项数÷2会使计算简单很多。
22.20人;(4n+4)人
【分析】根据所给的图,正确数出即可,在数的过程中,能够发现一张桌子能坐8个人,两张桌子能坐12个人多一张桌子就多4个人,根据这一规律,用字母表示为:4n+4;然后代入数字求解即可。
【详解】由分析可知:
4×4+4
=16+4
=20(人),
n张桌子可以坐(4n+4)人。
答:这样的4张桌子连在一起共可以坐20人,n张桌子可以坐(4n+4)人。
【点睛】此题主要考查了图形的变化,解题关键是分析题干得出规律,有一个桌时可坐8个人,以后每增加一个桌可增加4个人,根据此规律进行解答。
23.37.5cm
【分析】先求出上边1层高度,杯子叠起来的高度=1个杯子高度+1层高度×(杯子数量-1),据此分析。
【详解】(25-15)÷(5-1)
=10÷4
=2.5(厘米)
15+2.5×(10-1)
=15+2.5×9
=15+22.5
=37.5(厘米)
答:10个这样的杯子叠起来的高度是37.5厘米。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
24. n2 (n 1)2=n+n+1 210
【分析】观察题目给出的算式,发现前一个数都比后一个数大1,而且前一个数的平方减去后一个数的平方最终等于前数加后数,由此可得到规律。
【详解】(1)n2 (n 1)2=n+n+1
(2)
=20+19+18+17+……+2+1
=20×10+10
=200+10
=210
【点睛】本题考查学生的观察能力,找到规律然后利用规律是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八单元数与形经典题型练习卷(单元测试)-小学数学六年级上册人教版
题号 一 二 三 总分
得分
一、选择题
1.用小棒搭正方形,搭n个这样的正方形需要( )根小棒。
A. B. C.
2.照下面这样摆下去,摆n个三角形需要( )根火柴棒。
A.3n B.3n-1 C.2n+1 D.2n+3
3.如下图,照这样接着画下去,第10个图形有( )个黑色正方形,( )个白色正方形。
A.20;28 B.32;20 C.28;20 D.40;28
4.与的结果相同的是( )。
A.5×3 B. C. D.
5.找规律:3,7,15, …… 应填几,正确的是( )。
A.3×2+1=7,7×2+1=15,15×2+1=31,填31
B.3+4×1=7,7+4×2=15,15+15×3=60 ,填60
C.必须要写出4个数才能找出规律,“”里无法填出唯一的数
6.如图,每个小正方形都是由4根同样长的小棒摆成的。那么第8个图形中一共用( )根小棒。
A.324 B.144 C.160
7.数与形结合是一种重要的数学思想,认真观察下面的图形,“2020”这个数在_______个三角形的_______顶点处。应选( )。
A.673,左下 B.674,上 C.673,右下 D.674,左下
8.用灰、白两种六边形瓷砖按如图所示的规律拼成图案,继续拼下去,第10个图案中有( )块白色瓷砖。
第1个 第2个 第3个
A.10 B.40 C.42 D.60
二、填空题
9.观察下列各图形中正方形个数与直角三角形个数的关系,将下表填写完整。
正方形个数 1 2 3 4 5 …
直角三角形个数 0 4 8 ( ) ( ) …
10.如下图是小明用火柴搭的1条、2条、3条“金鱼”……,则搭n条“金鱼”需要火柴( )根。
11.用小棒按下面的方式搭图形,则第(16)个图形需要( )根小棒。
第(1)个 第(2)个 第(3)个
12.明明用小棒按照下面的方式摆六边形,摆n个六边形要用( )根小棒。
13.按规律填分数:、、、、、( )、( )。
14.仔细观察小黑点的排列,探索规律。
(1)第5幅图共有( )个点,第8幅图共有( )个点。
(2)第n幅图共有( )个点。
15.如图:……正方形按照这样的规律变换,当正方形有n个时,三角形有( )个。
16.找规律,写答案。
0.1÷11=0.0090909……
0.2÷11=0.0181818……
0.3÷11=0.0272727……
0.5÷11=( )
找一找,这个商的小数点后第2022个数字是( )。
三、解答题
17.
(1)像这样摆下去,第n个图形需要__________根小棒。
(2)当n=35时,计算第(1)题式子中需要的小棒数。
18.按如下规律摆放三角形,第五堆有多少个三角形?
19.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
20.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示,按照下面的规律摆下去。
(1)摆6个“金鱼”需要多少根火柴棒?
(2)摆n个“金鱼”需要多少根火柴棒?
(3)若有2018根火柴棒,那么可以摆多少个“金鱼”?
21.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点……按此规律第10个图中共有多少个点?第100个图形呢?
22.想一想,画一画,这样的4张桌子连在一起共可以坐多少人?n张呢?
23.如下图,1个杯子的高度是15cm,把5个完全一样的杯子叠起来的高度是25cm,那么10个这样的杯子叠起来的高度是多少厘米?
24.观察算式的规律:,,,,……。用含字母的式子表示规律:( )。
用规律计算:( )。
参考答案:
1.C
【分析】观察可知,小棒数量=正方形数量×3+1,据此分析。
【详解】n×3+1=3n+1(根)
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
2.C
【分析】分析图形可知,摆1个三角形需要3根火柴棒,摆2个三角形需要(3+2)根火柴棒,摆3个三角形需要(3+2+2)根火柴棒……每增加1个三角形就增加2根火柴棒,则摆n个三角形需要3+2(n-1)根火柴棒,据此解答。
【详解】摆n个三角形需要火柴棒的根数:3+2(n-1)=3+2n-2=2n+1
故答案为:C
【点睛】找出图形变化的规律是解答题目的关键。
3.A
【分析】分析题意,找出图形变化的规律,用含有字母的式子表示出第n个图形小正方形的总个数和黑色小正方形的个数;
白色小正方形的个数=小正方形的总个数-黑色小正方形的个数,据此解答。
【详解】第n个图形小正方形的总个数:4×(n+2)=4n+8
第n个图形黑色小正方形的个数:2n
第n个图形白色小正方形的个数:4n+8-2n=2n+8
当n=10时
黑色小正方形的个数:2n=2×10=20(个)
白色小正方形的个数:2n+8=2×10+8=28(个)
故答案为:A
【点睛】用含有字母的式子表示出图形变化的规律是解答题目的关键。
4.C
【分析】个连续奇数相加的和结果为,把拆为几个连续奇数相加的形式,利用公式即可求得。
【详解】
=34
故答案为:C
【点睛】本题考查数形结合思想在计算题中的应用。
5.C
【分析】结合题意,一一分析各个选项的正误,从而选出正确选项。
【详解】根据3,7,15, ……,可以至少得出两个符合它的规律,分别是A和B选项中的规律。那么可推出,必须要写出4个数才能找出确定的规律,那么“”里无法填出唯一的数。
故答案为:C
【点睛】本题考查了找规律,能从数字排列中找出规律是解题的关键。
6.B
【分析】根据上图中已知的规律:图形边长×边数,继续排列出第8个图形中一共有8×18根小棒。
【详解】图1有1×4
图2有2×6
图3有3×8
图4有4×10
图5有5×12
图6有6×14
图7有7×16
图8有8×18=144(根)
故选:B
【点睛】此题考查的是数形结合,关键是找出规律,再用规律解决问题。
7.B
【分析】从上图中发现:每一个三角形有3个顶点,用2020÷3=673(个)……1(个)也就是在第673个三角形后还余1个顶点,1个顶点正好在第674个三角形的上顶点处。
【详解】由分析可得,
2020÷3=673(个)……1(个)
所以,“2020”这个数在674个三角形的上顶点处。
故选:B
【点睛】此题考查的是数与形结合找规律,找出规律是解题关键。
8.C
【分析】观察图形发现,第一个图案有白色地砖6块,后边每多一个图案,则多4块白色地砖,根据这个规律,可确定第n个图案中有白色地砖的数量。
【详解】结合图形,第一个图案有白色地砖6块,后边每多一个图案,则多4块白色地砖,根据这个规律,可确定第n个图案中有白色地砖:4n+2块,
第10个图案中有白色瓷砖:
4×10+2
=40+2
=42(块)
故选:C
【点睛】本题考查的是图形的变化类问题,解题关键是图形结合,发现规律。
9. 12 16
【分析】经观察发现,每多1个正方形就多4个直角三角形,据此解答。
【详解】8+4=12(个)
12+4=16(个)
【点睛】本题主要考查数与形结合的规律,发现每多1个正方形就多4个直角三角形是解本题的关键。
10.6n+2
【分析】观察图形发现:搭1条金鱼需要火柴8根,搭2条金鱼需要14根,即发现了每多搭1条金鱼,需要多用6根火柴,则搭n条“金鱼”需要火柴8+6(n-1)=6n+2,据此即可解答问题。
【详解】根据分析得,每多搭一条金鱼,需要多用6根火柴。
8+6×(n-1)
=8+6n-6
=6n+2
所以搭n条金鱼需要火柴(6n+2)根。
【点睛】此类题找规律的时候一定要注意结合图形进行发现规律。
11.66
【分析】第一个图形:4×1+2=6根小棒组成,第二个图形:4×2+2=10根小棒组成,第三个图形:4×3+2=14根小棒组成,……那么第16个图形:4×16+2=66根小棒组成。
【详解】第一个图形中小棒数量:
4×1+2
=4+2
=6(根)
第二个图形中小棒数量:
4×2+2
=8+2
=10(根)
第三个图形中小棒数量:
4×3+2
=12+2
=14(根)
……
第16个图形中小棒数量:
4×16+2
=64+2
=66(根)
【点睛】此题考查了学生的观察能力和归纳能力,找出图形中小棒排列的规律,是解答此题的关键。
12.5n+1
【分析】由图可知,摆1个正六边形需要6根小棒,摆2个正六边形需要(6+5)根小棒,摆3个正六边形需要(6+5×2)根小棒,摆4个正六边形需要(6+5×3)根小棒……摆n个正六边形需要6+5(n-1)根小棒,据此解答。
【详解】分析可知,摆n个正六边形需要小棒的根数为:6+5(n-1)=6+5n-5=(5n+1)根。
【点睛】分析图形找出正六边形个数和小棒根数的变化规律是解答题目的关键。
13.
【分析】观察数列可知,各分数的分子按照1、3、5、7、9排列,相邻两个数的差是2;分母分别为4=22,9=32,16=42,25=52,36=62,所以后面两个分数的分母应为72=49,82=64。据此解答即可。
【详解】9+2=11,11+2=13
72=49,82=64
、、、、、、。
【点睛】本题考查数字排列规律,发现规律,利用规律是解题的关键。
14.(1) 30 72
(2)
【分析】根据图示,这组图形的规律为:第一幅图小黑点的个数为2个;第二幅图小黑点的个数:(个;第三幅图小黑点的个数为:(个;第n幅图小黑点的个数为:个。据此解答。
(1)
第一幅图小黑点的个数为2个
第二幅图小黑点的个数:(个
第三幅图小黑点的个数为:(个
第幅图小黑点的个数为:个
(1)
(个
(个
(2)
第n幅图共有个点。
【点睛】本题主要考查数与形结合的规律,关键根据图示发现规律,并运用规律做题。
15.4n-4
【分析】图1有1个正方形、0个三角形,图2有2个正方形、4个三角形,图3有3个正方形、8个三角形,图4有4个正方形、12个三角形……,三角形的个数=(正方形个数-1)×4;据此解答即可。
【详解】三角形的个数=(正方形个数-1)×4;当正方形有n个时,三角形的个数有:(n-1)×4=4n-4。
【点睛】探索图形的变换规律,运用图形的变换规律解答问题。
16. 0.0454545…… 4
【分析】仔细观察题中的式子可以发现:除数不变,被除数乘几,商也乘几,据此求出0.5÷11=0.0454545……;这个商的小数点后第2022个数字(总数位数循环节的位数。
【详解】0.5÷0.1=5
0.5÷11=0.0090909……×5=0.0454545……
0.5÷11的商是一个循环小数,这个循环小数的循环节是45,
(2022-1)÷2
=2021÷2
=101(组)……1(位)
余数1表示一个循环里的第1个数即4;所以这个商的小数点后第2022个数字是4。
【点睛】能发现题中的规律并利用规律求出0.5÷11的结果以及熟练掌握求循环小数第几位上数字是多少的方法是解题的关键。
17.(1)2n +1;
(2)71根
【分析】(1)观察图形可知:摆1个三角形需要3根小棒,可以写作:2×1+1;摆2个需要5根小棒,可以写作:2×2+1;摆3个需要7根小棒,可以写成:3×2+1;……摆n个三角形需要:(2n +1)根小棒。
(2) 根据第一小题的分析可知,摆n个三角形需要:(2n +1)根小棒,当n=35时,把数据代入计算,即可求当n=35时,需要小棒的数量。
【详解】(1)根据分析可知,像这样摆下去,第n个图形需要(2n+1)根小棒。
(2)35×2+1
=70+1
= 71(根)
答:摆35个三角形需要71根小棒。
【点睛】认真观察图形,并从中找出图形变化的规律,是解答此题的关键。
18.17个
【分析】这是一组等差数列,公差是3,从左到右依次加3。第1堆,5个△,5=3×1+2;第2堆,8个△,8=3×2+2;第3堆,11个△,11=3×3+2…第n堆,(3n+2)个△。
【详解】第1堆,5个△,5=3×1+2;
第2堆,8个△,8=3×2+2;
第3组,11个△,11=3×3+2
…
第n堆,(3n+2)个△。
当n=5时,
3×5+2
=15+2
=17(个)
答:第五堆有17个三角形。
【点睛】此题考查的是找规律,解答此题的关键是找到规律后,再根据规律解答就比较容易了。
19.(1)白:26个;黑:10个
(2)16
【分析】(1)第1个图形一共有(3×3)个小正方形,有1个黑色小正方形,有(3×3-1)个白色小正方形;
第2个图形一共有(3×4)个小正方形,有2个黑色小正方形,有(3×4-2)个白色小正方形;
第3个图形一共有(3×5)个小正方形,有3个黑色小正方形,有(3×3-3)个白色小正方形;
……
第n个图形一共有3(n+2)=(3n+6)个小正方形,有n个黑色小正方形,有3n+6-n=2n+6个白色小正方形;
(2)把白色小正方形的个数代入表示白色小正方形含有字母的式子,求出n的值即可。
【详解】(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
【点睛】分析图形找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
20.(1)38根;(2)2+6n;(3)336个
【分析】根据题意分析可得:搭第1个图形需8根火柴,此后,每个图形都比前一个图形多用6根,故按照上面的规律,摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根;据此解答。
【详解】(1)8+(6-1)×6
=8+5×6
=8+30
=38(根)
答:摆6个“金鱼”需要38根火柴棒。
(2)摆n条“金鱼”需用火柴棒的根数为8+(n-1)×6根;
(3)(2018-8)÷6+1
=2010÷6+1
=335+1
=336(个)
答:2018根火柴棒可以摆336个“金鱼”。
【点睛】本题是对图形变化规律的考查,查出前三个图形的火柴棒的根数,并观察出后一个图形比前一个图形多6根火柴棒是解题的关键。
21.166个;15151个
【分析】分析图形可知:第1个图形有(1+1×3)个点,第2个图形有(1+1×3+2×3)个点,第3个图形有(1+1×3+2×3+3×3)个点,……
由此规律可知第n个图形有(1+1×3+2×3+3×3+…+3n)个点,据此解答。
【详解】分析可知第n个图形有(1+1×3+2×3+3×3+…+3n)个点
当n=10时,1+1×3+2×3+3×3+…+3×10
=1+(1+2+3+…+10)×3
=1+(1+10)×10÷2×3
=1+11×10÷2×3
=1+110÷2×3
=1+55×3
=1+165
=166(个)
当n=100时,1+1×3+2×3+3×3+…+3×100
=1+(1+2+3+…+100)×3
=1+(1+100)×100÷2×3
=1+101×100÷2×3
=1+10100÷2×3
=1+5050×3
=1+15150
=15151(个)
答:第10个图中共有166个点,第100个图中共有15151个点。
【点睛】解决本题应用等差数列前n项和求和公式:(首项+末项)×项数÷2会使计算简单很多。
22.20人;(4n+4)人
【分析】根据所给的图,正确数出即可,在数的过程中,能够发现一张桌子能坐8个人,两张桌子能坐12个人多一张桌子就多4个人,根据这一规律,用字母表示为:4n+4;然后代入数字求解即可。
【详解】由分析可知:
4×4+4
=16+4
=20(人),
n张桌子可以坐(4n+4)人。
答:这样的4张桌子连在一起共可以坐20人,n张桌子可以坐(4n+4)人。
【点睛】此题主要考查了图形的变化,解题关键是分析题干得出规律,有一个桌时可坐8个人,以后每增加一个桌可增加4个人,根据此规律进行解答。
23.37.5cm
【分析】先求出上边1层高度,杯子叠起来的高度=1个杯子高度+1层高度×(杯子数量-1),据此分析。
【详解】(25-15)÷(5-1)
=10÷4
=2.5(厘米)
15+2.5×(10-1)
=15+2.5×9
=15+22.5
=37.5(厘米)
答:10个这样的杯子叠起来的高度是37.5厘米。
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
24. n2 (n 1)2=n+n+1 210
【分析】观察题目给出的算式,发现前一个数都比后一个数大1,而且前一个数的平方减去后一个数的平方最终等于前数加后数,由此可得到规律。
【详解】(1)n2 (n 1)2=n+n+1
(2)
=20+19+18+17+……+2+1
=20×10+10
=200+10
=210
【点睛】本题考查学生的观察能力,找到规律然后利用规律是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
